一種改進的飛行器動彎矩識別方法

周昊天，于開平

(哈爾濱工業大學航天學院，哈爾濱150001)

一種改進的飛行器動彎矩識別方法

周昊天，于開平

(哈爾濱工業大學航天學院，哈爾濱150001)

提出一種改進的飛行器動彎矩識別方法，該方法引入了頻域積分算法，避免了時域方法中消除趨勢項以及濾波所帶來的問題。對加速度響應進行兩次積分得到結構彈性位移響應，然后根據模態疊加理論求解出廣義坐標，最后結合模態彎矩識別截面的動彎矩響應。通過懸臂梁試驗驗證了算法的有效性，并與傳統方法識別出的結果進行對比。結果表明，新方法的識別結果更接近試驗實測動彎矩響應，具有更高的精度。最后將該方法應用于某型號飛行器，并給出了識別結果。

模態疊加法; 彎矩識別；頻域積分

0 引 言

火箭等飛行器在飛行過程中會受到復雜外力的作用。在這些外力的作用下，飛行器結構會產生動響應。為了使火箭等飛行器在飛行階段能夠平穩安全地運行，通常需要對結構各艙段的設計提出一定要求，比如強度、剛度、穩定性等。為了提出準確的指標要求，通常需要建立完整的飛行器結構動力學模型，在一定的初始條件和外力作用下進行仿真模擬，計算出結構各艙段的響應，而后可以根據響應得到各截面的彎矩、剪力等信息。然而在實際運行過程中，火箭等飛行器結構受到復雜外力作用，完全模擬復雜工況非常困難，因此通過已有的飛行或試驗數據進行內力識別可以作為重要的參考。

對于飛行器設計而言，內力的大小與分布是關系到飛行器能否達到設計目標的重要參數。飛行器在飛行過程中無法直接測量內力響應，雖然可以通過仿真的方法模擬飛行器受力情況計算出結構的動態內力響應，然而飛行器飛行過程中所受外力亦無法實測，同時飛行器實際工況復雜無法完全模擬，因此，出現了一些利用結構響應進行內力識別的方法。

當前國內外已經針對內力識別問題開展了一些研究，傳統方法采用結構的應變響應計算得到動彎矩[5]，這類方法通常容易受到飛行器結構的限制[6]。另外一些方法采用位移響應計算得到動內力。例如，龍源等[7]利用小波分析在時頻域都具有表征信號局部特征的特點，提出了一種識別固體火箭截面剪力和彎矩的方法；之后又對原方法做了很大改進，并對一固體火箭關鍵截面彎矩做了識別[4]。紀躍波等[8]根據虛功原理通過測量結構的位移響應，給出了與邊界條件無關的地下隧道內力識別結果。

飛行器在飛行過程中的位移響應無法直接測得，通常做法是在時域利用加速度響應進行二次積分獲得位移響應。然而在時域進行積分需要預先對數據進行濾波處理，在積分過程中會不可避免地引入趨勢項[4]，并且消除趨勢項本身也需要細致而復雜的調整過程。本文引入了加速度頻域積分方法，避免了原時域方法中選擇小波基函數以及小波分解層數等復雜過程，通過懸臂梁試驗驗證了本方法具有較高的識別精度，在工程應用中具備一定的實用價值。

1 截面彎矩識別的理論基礎

在工程實際中常把飛行器模型簡化為多自由度系統，再參照結構動力學中的模態疊加理論，認為幾何位移可以由n階廣義位移疊加而成：

(1)

式中：x(t)為測量點位置的幾何位移，ur為該點處第r階振型，qr(t)為第r階廣義坐標。從式(1)可以看出，若已知m(m>r)個測點處的幾何位移以及對應點處的前r階振型分量，則可以通過最小二乘方法計算出前r階的廣義坐標。另外可以通過理論計算或有限元等方法獲得對應點處各階模態彎矩及剪力，結合求得的廣義坐標，可以進行截面內力的識別：

(2)

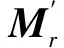
2 改進的截面彎矩識別方法

由第1節的理論可知，只要獲得飛行器的彈性位移響應，再結合理論推導或者仿真計算得出模態信息，即可進行結構動彎矩的識別工作。一般情況下很難直接測量飛行器的彈性位移響應，但可以利用測量到的加速度響應進行兩次積分獲得。對加速度響應積分一般采用時域積分方法，例如采用梯形公式。時域積分方法在積分過程中需要對數據進行消除趨勢項及濾波處理，否則無法獲得彈性位移，如圖1所示。

在實際應用中，常采用小波[9]或者經驗模態分解[7](Empiricalmodedecomposition,EMD)[10]作為消除趨勢項的手段，但無論是小波還是EMD方法都容易出現邊界效應[11]，使數據失真，如圖2所示。

鑒于內力識別僅需要彈性位移，這里考慮引入頻域積分方法[12]。頻域積分通過傅里葉變換將時域信號轉換到頻域上而后進行積分。

考慮一個離散時間加速度序列a(n)，其長度為N，對其進行離散傅里葉變換可以得到：

(3)

式中：a(k)為變換后的復數序列，f(k)為對應頻率，fs為采樣頻率。a(k)對應的簡諧波可以寫成如下形式：

a(t)k=Akcos(ωkt+φk)

(4)

其中，

(5)

對式(4)進行兩次積分，可得對應頻率下的位移諧波如下：

S(t)k=Askcos(ωskt+φsk)

(6)

其中，

(7)

因此，積分得到的位移表達式為：

(8)

如用F(x)表示傅里葉變換，用F-1(x)表示傅里葉逆變換，式(8)可以記為：

(9)

由式(9)可知，在頻域積分過程中，頻率小于1Hz的加速度諧波中的誤差被放大，同時考慮到需要消除剛體位移，需要對積分過程加以控制。本文采用的方法是低頻截止方法[13]，選定一個特定頻率fT，低于該頻率的加速度信號幅值置零。通過低頻截止處理可以有效避免低頻部分加速度信號誤差的放大效應，同時消除積分后的剛體位移。fT的選擇與加速度傳感器的頻率下限相關，一般應大于傳感器頻率下限。

3 試驗驗證與分析

在航天工程中，為了簡化計算，常采用梁模型代替全尺寸的飛行器模型，為了驗證算法的有效性，這里以懸臂梁為對象進行試驗研究。

懸臂鋼梁總長1200mm，寬50mm，厚9mm，五個加速度傳感器分別布置在距懸臂梁根部26、37、55、84、120cm的位置上，應變片位置距懸臂梁根部5cm，上下對稱布置，構成半橋測量結構，試驗裝置如圖3所示。

為了與飛行狀態下的飛行器工況相契合，這里采用寬頻的白噪聲進行激勵，利用采集到的加速度信號與仿真計算得到的懸臂梁振型、模態彎矩進行內力識別。

根據式(9)對加速度信號進行積分得到彈性位移響應如圖4所示，而后根據式(1)可得各階彈性廣義位移，如圖5所示。

一般而言，對于寬頻激勵下的結構響應，低階廣義位移貢獻較大而高階則趨向減少。對式(2)，根據經驗取前三階廣義位移進行內力識別即可得到較為理想的結果，為了與實測彎矩響應對比，這里對應變片位置處的彎矩進行識別，如圖6所示。從圖6可以看出，本文提出的頻域積分方法的識別結果與試驗實測結果相位一致，同時趨勢吻合程度較好，結果表明該方法可行且有效。

此外，與時域積分方法得到的結果相比，頻域積分方法的識別結果更接近實測值，見圖7。試驗結果表明，與時域積分方法相比，本文提出的頻域積分方法具有更高的識別精度。

在獲得各階彈性位移后，如果同樣已知其他任意截面處的模態彎矩則可以對該任意截面進行內力識別，圖8為距懸臂梁根部10cm處的動彎矩識別結果。

對于飛行器設計,關鍵截面處的最大載荷(內力)響應更值得關注。對飛行遙測數據進行處理，得到了飛行器飛行過程中的內力響應，如圖9所示。從圖9可以看出，該關鍵截面處的最大動彎矩發生在0.22s時刻，而設計人員預估最大值發生在0.2s左右，最大值絕對值為1.02左右，經比較兩者相對誤差小于5%，說明本方法可以為飛行器設計人員提供很好的參考與幫助。

4 結 論

對于無法直接測量的飛行器內力響應，本文給出了一種基于加速度頻域積分的識別方法，該方法避免了傳統時域積分方法中需要濾波以及消除趨勢項的步驟。本文通過懸臂梁試驗驗證了算法的有效性。試驗結果表明，與時域積分方法相比，本文提出的改進方法的識別結果與實測值更接近，具有更高的識別精度。最后，利用某型號飛行器遙測數據進行了動彎矩識別，改進方法識別出的最大動彎矩與設計人員預估的最大動彎矩非常接近。本文提出的改進方法對飛行器載荷設計與評估有重要的參考意義。

[1] 馬斌捷, 洪良友, 王國慶, 等. 火箭動態彎矩測量的頻響特性分析[J]. 強度與環境, 2012, 39(5): 1-6. [MaBin-jie,HongLiang-you,WangGuo-qing,etal.Frequencyresponsecharacteristicanalysisofthemeasurementaboutdynamicbendingmomentforlaunchvehicles[J].Structure&EnvironmentEngineering, 2012, 39(5): 1-6.]

[2] 洪良友, 馬斌捷, 賈亮, 等. 火箭結構動態載荷響應的非正交測點測量方法[J]. 導彈與航天運載技術, 2015,(4): 90-94. [HongLiang-you,MaBin-jie,JiaLiang,etal.Researchonthetechnologyofdynamicloadmeasurementusingnon-orthogonalmeasurepointsforlaunchvehicle[J].MissilesandSpaceVehicles, 2015,(4): 90-94.]

[3] 尹云玉. 固體火箭橫向響應載荷識別方法[J]. 宇航學報, 2009, 30(6): 2135-2139.[YinYun-yu.Theidentificationmethodoftransverserespondingloadforsolidrocket[J].JournalofAstronautics,2009, 30(6): 2135-2139.]

[4] 尹云玉. 固體火箭自由運行狀態截面彎矩識別方法[J]. 宇航學報, 2010, 31(7): 1706-1710. [YinYun-yu.Anidentificationmethodfortransverseresponsemomentofsolidrocketduringfreeflightstate[J].JournalofAstronautics, 2010, 31(7): 1706-1710.]

[5]FuentesR.Internalforcesofundergroundstructuresfromobserveddisplacements[J].TunnellingandUndergroundSpaceTechnology, 2015, 49: 50-66.

[6] 周哲, 莊良杰, 熊正南, 等. 基于小波分析的陀螺漂移趨勢項提取[J]. 中國慣性技術學報, 1999,7(4): 59-61.[ZhouZhe,ZhuangLiang-jie,XiongZheng-nan,etal.TrendextractionofGyro'sdriftbasedonwaveletanalysis[J].JournalofChineseInertialTechnology, 1999,7(4): 59-61.]

[7] 龍源, 謝全民, 鐘明壽, 等. 爆破震動測試信號預處理分析中趨勢項去除方法研究[J]. 工程力學, 2012, 29(10): 63-68. [LongYuan,XieQuan-min,ZhongMing-shou,etal.Researchontrendremovingmethodsinpreprocessinganalysisblastingvibrationmonitoringsignals[J].EngineeringMechanics, 2012, 29(10): 63-68.]

[8] 紀躍波, 秦樹人, 柏林, 等. 有限區間信號邊界效應問題的研究[J]. 振動與沖擊, 2002, 21(4): 108-111. [JiYue-bo,QinShu-ren,BaiLin,etal.Researchontheedgeeffectofcutoffsignalwithlimitedtimedomain[J].JournalofVibrationandShock, 2002, 21(4): 108-111.]

[9] 徐慶華. 試采用FFT方法實現加速度、速度與位移的相互轉換[J]. 振動、測試與診斷, 1997, 17(4): 30-34. [XuQing-hua.Conversionbetweenvibrationalacceleration,velocityanddisplacementusingFFT[J].JournalofVibration,Measurement&Diagnosis, 1997, 17(4): 30-34.]

[10] 蔣良濰, 姚令侃, 吳偉. 邊坡振動臺模型實驗動位移的加速度時程積分探討[J]. 防災減災工程學報, 2009, 29(3): 261-266. [JiangLiang-wei,YaoLing-kan,WuWei.Studyoncalculationofdynamicdisplacementfromtimeintegrationofaccelerationinshakingtablemodeltestsofsideslope[J].JournalofDisasterPreventionandMitigationEngineering, 2009, 29(3): 261-266.]

通信地址：哈爾濱工業大學344信箱(150001)

電話：(0451)86414320

E-mail:szzhouhaotian@126.com

于開平(1968-)，男，博士，教授，主要從事結構動力學研究。本文通信作者。

通信地址：哈爾濱工業大學344信箱(150001)

電話：(0451)86414320

E-mail:yukp@hit.edu.cn

(編輯：牛苗苗)

An Improved Identification Method for Dynamic Bending Moment Responses of Flight Vehicles

ZHOU Hao-tian, YU Kai-ping

(School of Astronautics, Harbin Institute of Technology, Harbin 150001，China)

An improved identification method based on the mode superposition method for dynamic bending moment responses of flight vehicles is proposed in this paper. A frequency domain integration algorithm is introduced to avoid the problems caused by the tendency eliminating and signal filtering when using the time-domain integration method. Firstly, the displacement response of the flight vehicle is obtained by integrating the acceleration responses twice. Then, the generalized displacement is calculated by the mode superposition method. Finally, the dynamic bending moment response is identified by utilizing the modal moment. The validity of this approach is verified through an experiment on a cantilever beam, where the results identified by using both the time-domain integration and frequency-domain integration method are presented. It is demonstrated that the results obtained by the improved method are closer to the real moments than that obtained by the classical time-domain method, namely the improved method has a higher accuracy. Furthermore, the proposed method is applied to estimate the dynamic bending moment responses of a vehicle during the flight, and the results are given.

Mode superposition method; Response moment identification；Frequency-domain integration

2016-09-13;

2016-12-15

國家自然科學基金(11372084)

V421

A

1000-1328(2017)03-0248-05

10.3873/j.issn.1000-1328.2017.03.004

周昊天(1989-)，男，博士生，主要從事結構動力學反問題研究。