應用偽譜法的運載火箭在線制導方法研究

張志國，余夢倫，耿光有，宋 強

(北京宇航系統工程研究所，北京100076)

應用偽譜法的運載火箭在線制導方法研究

張志國，余夢倫，耿光有，宋 強

(北京宇航系統工程研究所，北京100076)

研究Gauss偽譜法(GPM)在液體運載火箭拋罩結束到入軌飛行段制導律設計中的應用性。在每一個制導周期內，采用高效高精度數值軌跡優化方法計算當前制導周期內的制導律。通過合理選擇非線性規劃問題的基點數量和制導周期，節省制導方法計算時間。將基于偽譜法的制導方法與運載火箭中使用的迭代制導方法進行對比，在保證同等入軌精度的條件下，該方法對于復雜約束問題處理方法更為便捷，滿足在線制導的需求。同時仿真表明,該方法能夠有效應對各種偏差，是比較接近工程應用的一種方法。

偽譜法；實時在線制導；軌跡優化；非線性規劃(NLP)

0 引 言

制導技術是影響飛行器性能的關鍵技術，從國內外運載火箭的發展歷程來看，制導方法經歷了從開環制導到閉環制導，從攝動制導、迭代制導到實時在線預測制導的發展。制導方法的發展主要圍繞兩個關鍵問題，即制導精度和制導效率。傳統制導方法受硬件性能限制，為保證制導效率主要采用解析方法，犧牲了部分制導精度，如攝動制導，射前裝訂好制導參數，可以在線實時制導，但精度不高。隨后迭代制導方法的出現，提升了火箭的制導精度，但由于迭代制導在方法中對引力場采用了近似處理，方法誤差無法完全消除，同時迭代制導對末端程序角不加限制，無法控制火箭入軌的姿態，對于有姿態需求的任務需要單獨增加調姿段。隨著計算機技術的發展，使得高精度的制導數值計算方法成為可能，尤其是高效高精度軌跡優化計算方法的發展，衍生出了一系列基于軌跡優化方法的制導新方法。如基于數值間接法、直接法[1]、混合法[2]軌跡優化的制導方法，本文采用的偽譜法即為直接法中的一種。

每一次制導運算實際上是進行一次軌跡優化計算，只是不需要獲得全局優化和控制參數，而只需要獲得當前制導周期內的控制變量。基于數值間接法的制導方法受到間接法初值敏感，計算時間長而在當前計算機條件下實時制導應用受到限制。基于直接法的制導方法通過合理選擇問題的階數，一方面相對間接法能夠節省制導方法計算時間，另一方面針對復雜的約束條件仍能獲得較高的制導精度。是比較接近工程的一種方法。

偽譜法[3-4]將高度非線性微分方程的解用插值多項式表示出來，即通過有限個離散基點來近似狀態變量和控制變量，相應基點處的微分方程、約束條件和系統積分指標都可以表示成基點的代數方程。原微分問題轉化為標準非線性規劃(Nonlinear programming, NLP)問題，對于大規模NLP問題的求解方法主要有序列二次規劃(Sequential quadratic programming, SQP)法和內點法，基于這兩種方法已有一些成熟的軟件，如基于SQP方法的SNOPT[5]、NPSOL等軟件，基于內點法的IPOPT軟件[6]，近年來，這些方法均得到了快速發展，使得偽譜法的應用越來越廣泛。

偽譜法在應用過程中，若在Matlab環境下編程(如：采用GPOPS工具箱)，計算精度高但效率偏低，適合用于離線計算，如文獻[7]中求解月球定點著陸問題和文獻[8]求解固體火箭上升段軌跡優化問題，計算耗時為分鐘的量級。若要提高數值方法計算效率，從而滿足在線軌跡規劃和制導律設計的實時性需求，解決思路包括采用更高效的編程環境、簡化問題模型、改進NLP問題求解方法的效率等，如文獻[9]將軌跡跟蹤制導問題轉化為線性時變系統調節器問題來進行求解，文獻[10]中采用狀態量縮減的方法改進閉環制導方法的計算效率。

本文采用C語言版本SNOPT求解器，通過選取不同配點和制導周期，比較得出合適的制導參數選取方案，在保證入軌精度的同時，進一步提高制導律的求解效率，滿足在線設計需求。該方法能夠有效處理帶末端姿態約束火箭制導問題，處理過程簡便，并能很好地適應一定范圍內的雙向偏差。

1 偽譜法軌跡優化方法

已知一般的非線性系統最優控制問題，包括狀態方程、等式(不等式)約束、性能指標三部分，整個最優控制問題要求在滿足狀態方程和等式(不等式)約束的條件下，使得性能指標達到極小值，統一形式可以寫為：

(1)

式中：x(t)、u(t)分別表示狀態變量和控制變量，t0、tf分別表示最優控制問題的起始時間和末端時間，E和C分別表示等式約束和不等式約束。偽譜法插值多項式的選擇主要有Legendre多項式和Chebyshev多項式兩種，根據基點位置、插值多項式種類、積分形式的不同選取方法，偽譜法分為Legendre偽譜法、Gauss偽譜法、Radau偽譜法和Chebyshev偽譜法，幾種方法的計算效率和精度相當[11]，其中Gauss偽譜法的解滿足庫恩-塔克(Karush-Kuhn-Tucker,KKT)條件，利用余向量映射定理，可以證明Gauss偽譜法的解同間接法的解具有一致完備性，因此在軌跡優化問題中被廣泛采用[12]。本文采用Gauss偽譜法，配點選擇正交Legendre多項式的零點，積分采用Gauss積分公式，正交Legendre多項式的基點在(-1,1)之間取值，需要首先將時間變量[t0,tf]投影變換到[-1,1]內。

(2)

將連續最優控制問題轉換為以Legendre-Gauss基點處的狀態變量和控制變量為未知系數的標準NLP問題[4]。

(3)

式中：k為有限的離散基點，Xk、Uk分別為離散時刻τk處的狀態變量和控制變量。采用Lagrange插值，Dk,i為Lagrange插值多項式的導數，用于計算狀態量微分方程的等式約束。wk為Gauss積分公式中的積分權重，當基點數給定時為常值。其中Dk,i的表達式為

(4)

對于式(3)構成的適當規模的NLP問題，目前有多種數值方法可以高效地給出求解結果。

2 基于偽譜法的實時在線制導方法

火箭與導彈的制導目標不同，火箭需要瞄準目標軌道根數。迭代制導開始作用在拋罩后飛行段[13]。本文基于偽譜法的實時制導方法選擇同樣飛行狀態作為初始狀態，制導開始時，火箭已經拋掉整流罩，在真空飛行，沒有空氣動力，主要受到重力和發動機推力影響，發動機參數偏差，主要包括比沖、推進劑秒耗量偏差，推力作用線橫移和偏斜等。飛行過程中做瞬時平衡假設，制導參數的選取僅包括俯仰角和偏航角兩個變量。因此火箭動力學微分方程可以寫為：

(5)

式中：狀態量x、y、z，Vx、Vy、Vz，m分別表示火箭的位置，速度和質量。控制量φ、ψ分別表示火箭的俯仰程序角和偏航程序角。F(t) 表示火箭發動機的推力。性能指標函數為：

(6)

對于推力大小不可調的火箭來說，時間最優性能指標等價于燃料最優。考慮一級飛行結束時程序角已經固定，因此制導開始時，程序角初值是問題的一個約束，如果考慮火箭末端姿態，過程中角加速度限制，最優問題的約束方程可以寫為：

(7)

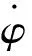
(8)

(9)

在每個制導周期內，根據火箭當前的狀態量，進行一次偽譜法軌跡優化計算，獲得剩余飛行時間內的控制變量基點值，通過Lagrange插值得到當前狀態下的控制量，僅取當前控制量作為火箭制導控制參數

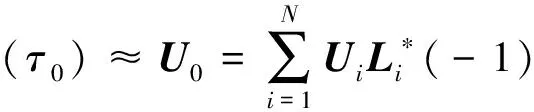
(10)

式中：U0(τ=-1)即為當前時刻的制導律。飛行全過程按照此方法進行滾動時域優化控制，即可實現火箭實時在線制導，基于偽譜法的實時在線制導流程如圖1所示。

偽譜法最大的優勢在于能夠用更少的參數得到較高的計算精度。從理論上講，插值點選取的越多，計算結果精度將越高，但是隨著基點的增多將帶來計算量和計算時間的大大增加，這將使直接法計算效率的優勢不再明顯。下面分別選擇基點數=4、8、12三種情況進行單次偽譜法軌跡優化方法計算，選擇同樣的收斂控制精度，統計單步偽譜法的計算時間，并獲得俯仰角和偏航角變化曲線圖2和圖3(數值仿真過程采用臺式機CPU3.19GHZ，內存1.93GB)。

表1 不同基點數量條件下偽譜制導法計算效率

由表1可知，選擇同等要求的數值算法收斂精度，隨著離散基點數量的增加，單步偽譜法計算時間不斷增加，對于很少的基點，偽譜法仍然能夠得到較高的收斂精度，但注意該精度是插值意義下的收斂精度，即保證通過配點進行Lagrange插值得到的末端狀態收斂精度。

實時制導周期的選擇至少要大于單步計算周期，考慮到選擇8～12個基點的單步偽譜法計算周期在100～200 ms的量級，本文分別采用10 s、5 s和1 s三種制導周期進行實時制導方法計算，仿真結果如圖4和圖5所示。考察不同制導周期對入軌精度的影響，同時用制導周期為1 s的迭代制導[15]入軌精度作對比。

從位置速度和軌道根數同標稱入軌條件的偏差(見表2和表3)可以看出，偽譜制導法選取的制導周期越短，入軌精度越高，并且和迭代制導能夠獲得同樣量級的入軌精度。圖5的偏航程序角歷程和圖3有一定的差異，是由于圖3為單次全局軌跡優化曲線；圖5為周期制導曲線，控制量通過偽譜法的有限個基點插值獲得，并且在每個制導周期內才更新，導致積分獲得的狀態量和標準彈道略有差異，求解最優控制問題進而引起偏航程序角微小變化。偏航程序角設計是在0°附近，火箭基本在射面內飛行，雖然圖上顯示趨勢不同，但是相對量級很小(在1°以內)，符合工程設計要求。而俯仰程序角由于基準值較大，圖4和圖2曲線一致。

在制導末段，為了防止制導程序角出現不穩定情況，在最后兩到三個制導周期內不進行偽譜法更新計算，而是采用前一個制導周期已經求得的末端最優制導程序角進行插值。因此和末端近似的迭代制導方法獲得同等量級的入軌精度，如果想進一步提升入軌精度并且工程上可用，無論何種方法都需要首先解決末端程序角跳變不穩定問題。但其實當前方法的入軌精度相對于導航精度已經足夠。

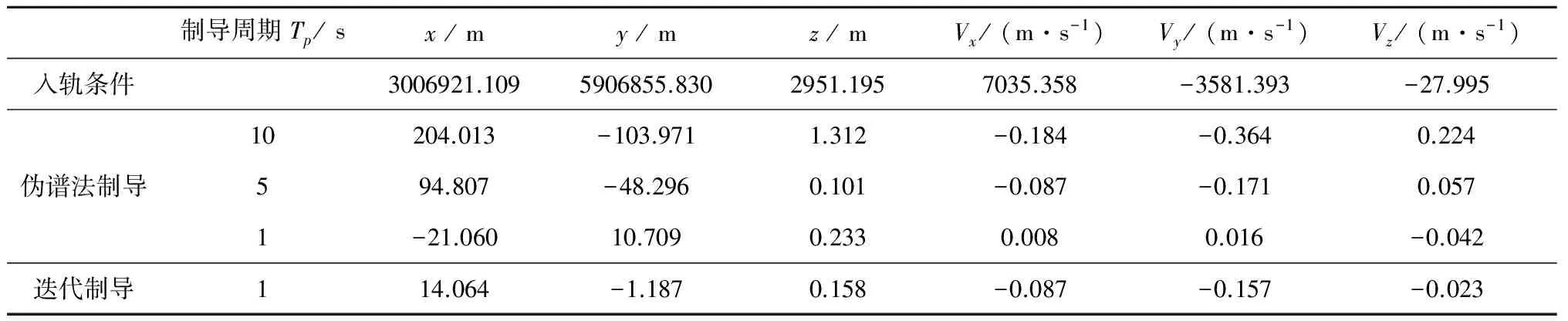
表2 不同制導周期下位置速度入軌精度

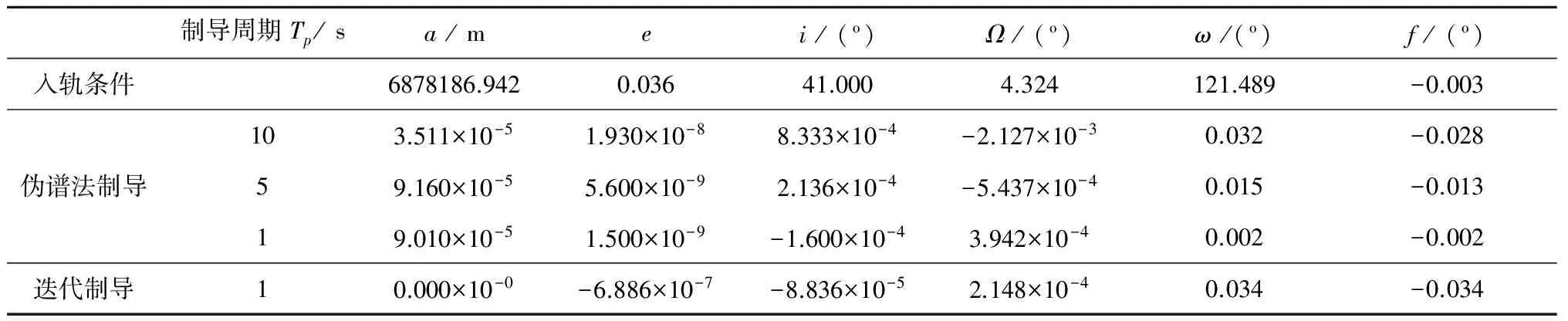
表3 不同制導周期下軌道根數入軌精度

表4 不同末端條件下軌道根數的入軌精度

3 末端帶約束制導方法研究

迭代制導對末端程序角不加限制，無法控制火箭入軌的姿態，但對于基于偽譜法的制導方法不存在這一問題，因為偽譜法的優勢就在于處理約束復雜的問題，無論是過程約束還是末端約束，不需要解析推導新的一階必要條件，僅需通過將約束施加在原問題的離散點上，即可求得有約束問題的制導律控制。考慮末端有姿態角約束的問題，分別選擇俯仰角-10°、-20°、-30°三種狀態，偏航角0°、-2°、+2°三種狀態，用偽譜制導法進行制導控制得到軌道根數的入軌精度(見表4)。

從圖6和圖7可以看出，對于末端有姿態角約束的問題，基于偽譜法的制導算法能夠獲得與末端無約束問題同等量級入軌精度的制導率，入軌軌道根數中半長軸、偏心率、軌道傾角、升交點赤經均在1.0×10-4(°)量級以下，唯一變化的是影響入軌位置的真近點角，這是由于對于火箭來說，不考慮發動機搖擺，火箭的姿態決定了推力的方向，同時假設火箭一直滿推的情況，當末端增加姿態約束時，如果目標仍然瞄準初始設計的全部六個軌道根數，新的最優軌跡可能已不再是運載能力最優的軌跡[14]，因此需要放松一個瞄準參數，即真近點角，調整合適的入軌位置，保證運載能力最大，如果采用緯度幅角參數(u=ω+f)，則其入軌精度也可達到1.0×10-4(°)量級。

從不同末端約束條件下的控制程序角曲線(圖6和圖7)可以看出，俯仰和偏航程序角的斜率都發生了變化，也可以從另一個側面說明新的制導控制飛行路線已經不再是原來的標準彈道，如果初始程序角沒有變化，真正決定施加末端約束條件下能否可控的條件是角加速度的控制能力，尤其是初始程序角能否快速過渡到最優控制程序角曲線上來。另一方面，該方法在控制末端程序角雖然采用插值控制，但基本是線性變化，即無論前期程序角如何變化，末端程序角都表現為線性控制，這樣利于工程實施的可行性和制導控制的可靠性。

4 制導方法應對偏差的收斂性

火箭實際飛行過程中會受到各種偏差干擾的影響，因此需要考察制導方法對于各種偏差的適應性。理論上只要偏差沒有超出火箭能力所能到達的范圍時，制導方法應該能夠應對各種偏差并且控制火箭到達既定軌道。這里參考茹家欣[13]在迭代制導方法中加偏差測試的方法，將火箭各種狀態偏差折合到出發時刻的偏差。文中考慮火箭二級飛行段制導律設計，因為二級飛行初始偏差主要來自于起飛和一級飛行段，火箭制導的誤差來源主要包括工具誤差和方法誤差：工具誤差的主要來源是慣性器件的測量偏差，根據現有一級飛行段工程中使用的慣性器件所能達到的測量精度進行估算，如速度、位置的偏差；方法誤差包括質量、發動機偏差、環境等因素，如文中考慮質量約±1%的偏差。分別考慮正負極偏差的情況，選擇同樣的入軌條件，得到基于偽譜法的制導方法應對偏差制導結果如表5所示。

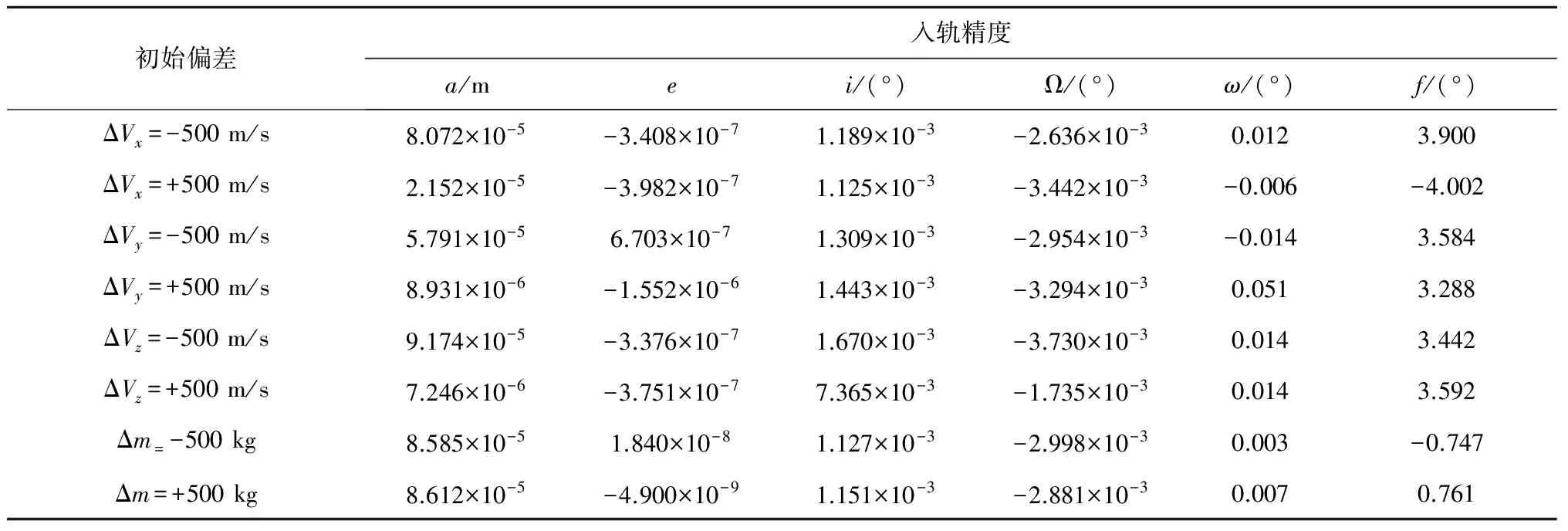
表5 正負極初始偏差條件下軌道根數的入軌精度

對于含偏差問題，如果瞄準初始設計的六個軌道根數，同樣有運載能力變化的問題，因此仍然考慮瞄準五個入軌軌道根數，調整入軌位置，將真近點角約束放松作為f0±10°的約束，通過施加幾組正負偏差，數值仿真表明，偽譜制導法都能夠很好的適應，并且保證較高的入軌精度。

5 結束語

本文設計了基于偽譜法的運載火箭在線制導方法，針對火箭拋罩結束到入軌動力飛行段制導律進行數值仿真，結果表明基于偽譜法的制導方法應用于實時制導律設計時，確有較高的制導效率和制導精度，可以和迭代制導有同樣甚至更高的入軌精度。選擇合適的基點數量和制導周期可以平衡制導效率和制導精度的關系。該方法在處理多約束制導問題時處理簡單，效率高，并且能很好的適應一定范圍內的雙向偏差，為偽譜制導方法的工程應用提供一定參考。

[1] Lu P, Pan B. Highly constrained optimal launch ascent guidance[J]. Journal of Guidance Control & Dynamics, 2012, 33(2):404-414.

[2] 崔乃剛, 黃盤興, 韋常柱, 等. 基于混合優化的運載器大氣層內閉環制導方法[J]. 中國慣性技術學報, 2015,23(3):328-333. [Cui Nai-gang, Huang Pan-xing, Wei Chang-zhu, et al．Colsed-loop endo-atmospheric guidance of launch vehicle based on hybrid optimization approach [J]. Journal of Chinese Inertial Technology, 2015,23(3):328-333.]

[3] Fahroo F, Michael I. Advances in Pseudo-spectral methods for optimal control[C]. AIAA Guidance, Navigation and Control Conference, Honolulu, Hawaii, USA, August 18-21, 2008.

[4] 孫勇. 基于改進Gauss偽譜法的高超聲速飛行器軌跡優化與制導[D]. 哈爾濱: 哈爾濱工業大學, 2012. [Sun Yong. Trajectory optimization and guidance of hypersonic vehicle based on improved Gauss Pseudo-spectral method [D]. Harbin: Harbin Institute of Technology, 2012.]

[5] Gill P E, Murray W, Saunders M A. SNOPT: An SQP algorithm for large scale constrained optimization [J]. SIAM Journal on Optimization, 2002, 12(4):979-1006.

[6] W?chter A, Biegler L T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming [J]. Mathematical Programming, 2006, 106(1):25-57.

[7] 彭祺擘, 李海陽, 沈紅新. 基于高斯—偽譜法的月球定點著陸軌道快速優化設計[J]. 宇航學報, 2010, 31(4):1012-1016. [Peng Qi-bo, Li Hai-yang, Shen Hong-xin. Rapid lunar exact-landing trajectory optimization via gauss Pseudo-spectral method [J]. Journal of Astronautics, 2010, 31(4):1012-1016.]

[8] 楊希祥, 張為華. 基于Gauss偽譜法的固體運載火箭上升段軌跡快速優化研究[J]. 宇航學報, 2011, 32(1):15-21. [Yang Xi-xiang, Zhang Wei-hua. Rapid optimization of ascent trajectory for solid launch vehicles based on Gauss Pseudo-spectral method [J]. Journal of Astronautics, 2011, 32(1):15-21.]

[9] 廖宇新, 李惠峰, 包為民. 基于間接Radau偽譜法的滑翔段軌跡跟蹤制導律[J]. 宇航學報, 2015, 36(12):1398-1405. [Liao Yu-xin, Li Hui-feng, Bao Wei-min. Gliding trajectory tracking guidance law based on indirect Radau Pseudo-spectral method [J]. Journal of Astronautics, 2015, 36(12):1398-1405.]

[10] 閆循良, 廖守億, 何泰,等. 基于改進偽譜反饋控制的遠程變軌閉環制導[J]. 宇航學報, 2016, 37(1):84-93. [Yan Xun-liang, Liao Shou-yi, He Tai, et al. Modified Pseudo-spectral feedback control based closed-loop guidance for long-range orbit maneuver [J]. Journal of Astronautics, 2016, 37(1):84-93.]

[11] Huntington G T, Benson D, Rao A V. A comparison of accuracy and computational efficiency of three pseudo-spectral methods[C]. Proceedings of the AIAA Guidance, Navigation, and Control Conference, Washington, DC, USA, 2007.

[12] Drake D, Xin M, Balakrishnan S N. New nonlinear control technique for ascent phase of reusable launch vehicles [J]. Journal of Guidance, Control, and Dynamics, 2004, 27(6):930-937.

[13] 茹家欣. 液體運載火箭的一種迭代制導方法[J], 中國科學, 2009, 39(4):696-706. [Ru Jia-xin. An iterative guidance method of liquid rocket [J]. Science in China, 2009, 39(4):696-706.]

[14] 韓祝齋. 用于大型運載火箭的迭代制導方法[J]. 宇航學報, 1983(1). [Han Zhu-zhai. An iterative guidance method for the large launch vehicle [J]. Journal of Astronautics, 1983(1).]

[15] 陳新民, 余夢倫. 迭代制導在運載火箭上的應用研究[J]. 宇航學報, 2003, 24(5):484-489. [Chen Xin-min, Yu Meng-lun. Study of iterative guidance application to launch vehicles [J]. Journal of Astronautics, 2003, 24(5):484-489.]

通信地址：北京市豐臺區南大紅門路1號(100076)

電話：(010)68758250

E-mail:zhangzhiguo08@yeah.net

(編輯：牛苗苗)

Research on Application of Pseudo-Spectral Method in Online Guidance Method for a Launch Vehicle

ZHANG Zhi-guo, YU Meng-lun, GENG Guang-you, SONG Qiang

(Beijing Institute of Aerospace System Engineering, Beijing 100076, China)

The study conducts an application research on the guidance law design of the ascent trajectory for a launch vehicle based on the Gauss pseudo-spectral method (GPM). During each period, high efficiency and high precision trajectory optimization numerical methods are used to design the current guidance law. Through making appropriate choices about the number of nodes and the period of guidance, this method is not only to reduce the calculation time, but also to solve the constrained problem rapidly. Compared to the iterative guidance method, the GPM guidance method is much more easily to deal with the constrained problem under the same orbit injection precision. Simulations indicate that this method can also effectively deal with a variety of deviations, so it is very closer to the engineering application.

Pseudo-spectral method; Real-time online guidance; Trajectory optimization; Nonlinear programming (NLP)

2016-09-05;

2017-01-03

V448.13

A

1000-1328(2017)03-0262-08

10.3873/j.issn.1000-1328.2017.03.006

張志國(1991-)，男，博士生，主要從事飛行器軌跡優化、制導與控制方法研究。