基于數據挖掘的房地產價格預測
孫珊珊


摘 要: 針對當前房地產價格預測精度低的難題,提出基于數據挖掘的房地產價格預測模型。首先對當前房地產價格預測研究的現狀進行分析,指出房地產價格變化的混沌性和隨機性;然后采用混沌理論對數據進行預處理,重建房地產價格預測模型的樣本,并采用相關向量機建立房地產價格預測模型;最后采用房地產價格數據進行驗證性測試。該模型可以描述房地產價格歷史數據中隱藏的變化特點,獲得了比其他模型更優的房地產價格預測結果。
關鍵詞: 房地產市場; 價格預測; 混沌性變化; 非線性擬合
中圖分類號: TN911?34; TP391 文獻標識碼: A 文章編號: 1004?373X(2017)05?0126?04
Abstract: Since the prediction accuracy of the current real estate price is low, a real estate price forecasting model based on data mining is proposed. The study situation of the current real estate price prediction is analyzed to point out the chaos characteristics and randomness of the real estate price variation. The chaos theory is used to preprocess the data, and reconstruct the samples of the real estate price prediction model. The relevance vector machine is adopted to set up the real estate price prediction model. The data of the real estate price is employed to conduct the verification test. The model can describe the hidden change characteristics existing in the historical data of the real estate price, and obtain a better prediction result than that of other models.
Keywords: real estate market; price forecast; chaos change; nonlinear fitting
0 引 言
隨著經濟不斷發展和城市化進程的加快,房地產市場異常活動,房地產價格不斷上升,同時房地產價格還受到一個地區的經濟、國家政策以及綜合影響,房地產價格有時會出現一定的下降,因此房地產價格變化具有一定的規律性和隨機性[1]。對房地產價格進行預測,可以幫助政府和企業掌握一個地區、國家的房地產市場變化趨勢,維護社會安全和團結,因此房地產價格建模與分析成為當前房地產市場中一個十分活躍的研究方向[2]。
為了有效地對房地產價格進行預測,人們對其進行相關分析和研究,房地產價格預測模型大致可以劃分為兩個階段:傳統預測模型階段和現代預測模型階段[3],傳統模型主要有多元線性回歸法,它通過擬合房地產價格的影響因子與房地產價格之間的變化關系,確定回歸模型的相關參數值,從而對房地產價格將來的變化趨勢進行估計,為房地產價格預測做出了一定的貢獻,然而該類模型缺陷十分明顯,因為假設房地產價格永遠呈直線上升趨勢,這與房地產價格的實際變化特點不相符,這主要是由于房地產價格的影響因素很多,因素間又相互影響以及干擾,導致房地產價格具有周期性,同時具有隨機性,甚至具有一定的混沌特性[4?5]。現代模型主要針對房地產價格的隨機性和混沌性進行建模,主要有神經網絡、支持向量機等,可以反映房地產價格的隨機性以及混沌性,獲得了比傳統模型更優的房地產價格的預測結果[6?8]。
相關向量機(Relevance Vector Machine,RVM)是基于現代統計學理論的數據挖掘技術,集成了神經網絡學習效率高和支持向量機預測效果好的優點,在網絡流量、經濟時間序列等領域取得了不錯的應用效果,為房地產價格預測提供了一種新的建模工具[9]。為了進一步提高房地產價格預測精度,本文提出基于數據挖掘的房地產價格預測模型。
1 房地產價格預測模型的總體設計
一個地區的房地產價格受到一系列因素的綜合影響,價格波動范圍很大,通常根據時間先后對房地產價格數據進行收集,它們組合成為一個時間序列[{x1,x2,…,xn},]當前時間點的房地產價格[xi]可能與[d]個相近時間點的房地產價格之間有一定的關聯,因此可以將[d]個相近房地產價格值作為[xi]的輸入,構建如下的數學模型:
擬合函數[f( )]的選擇直接決定了房地產價格預測結果的好壞,為了解決神經網絡預測精度低、過擬合和支持向量機學習效率低的缺陷,本文采用性能優異的相關向量機作為[f( )],建立整體性能優異的房地產價格預測模型,其總體框架如圖1所示。
2 相關向量機描述
(2) 針對房地產價格的混沌性和隨機性,采用混沌理論確定其輸入向量數量,重建房地產價格學習樣本。
(3) 采用RBF函數作為相關向量機的核函數,將訓練集輸入到相關向量機進行學習,并對相關參數進行優化,建立房地產價格模型。
4 房地產價格預測的實證分析
4.1 房地產價格數據
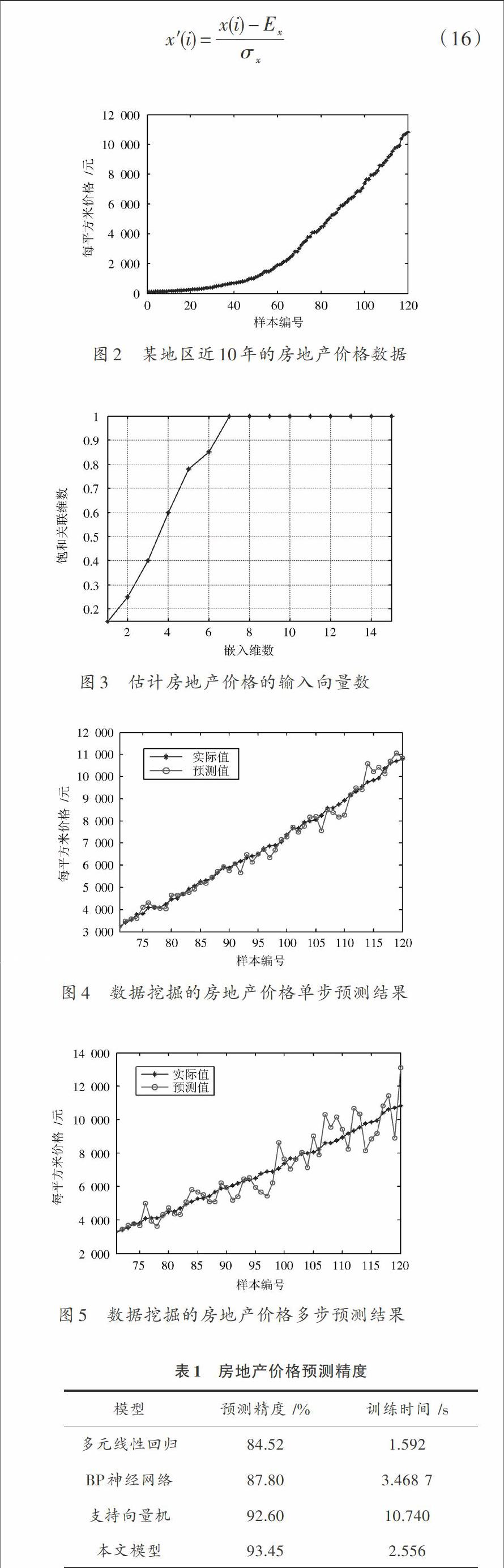
為了測試數據挖掘的房地產價格預測效果,采用某地區近10年的房地產價格數據作為研究對象,共有120個時間序列點,具體見圖2。最近的50個時間序列點作為驗證集,其他時間序列點用于建立房地產價格預測模型。
4.2 估計輸入向量的數量
由于房地產價格數據的混沌性較弱,因此采用關聯維法估計輸入向量的數量,結果如圖3所示。
對圖3進行分析可以清楚地看出,當輸入向量數據的數量達到7時,此時房地產價格的關聯維數已經不再發生變化,十分穩定,即該房地產價格的最優輸入向量數為7,這表示當前時間點的房地產價格值受到最近7個時間點房地產價格的影響,否則重建房地產價格的時間序列。
4.3 實驗結果
50個房地產價格驗證樣本的單步預測結果如圖4所示,對圖4中的房地產價格預測結果進行分析可以發現,采用數據挖掘技術可以發現房地產價格的變化特點,得到了較高的預測精度,而且房地產價格的預測偏差變化幅度小,變化十分平穩,這表明房地產價格預測結果是可靠的,有一定的實際應用價值。
房地產價格的建模與預測主要是對將來房地產價格的變化趨勢進行把握,單步預測結果的實際應用范圍有一定的局限性,因此需要進行多步提前的房地產價格預測,本文模型的提前4步房地產價格預測結果如圖5所示。對圖5的多步房地產價格預測結果進行分析可知,本文模型的多步房地產價格預測誤差明顯要大于單步預測誤差,預測精度相應降低,然而房地產價格整體趨勢預測好可以幫助人們了解房地產價格市場的變化趨勢,具有十分重要的應用價值。
為了進一步分析數據挖掘的房地產價格建模與預測優越性,采用多元線性回歸法、支持向量機[10]、BP神經網絡[11]對相同數據進行建模與預測,統計它們的預測精度和執行時間,結果如表1所示。
對從表1的預測精度和執行時間進行分析,可以得到如下結論:
(1) 在所有模型中,多元線性回歸法的建模速度比較快,房地產價格預測誤差最大,預測精度最低,是因為其屬于線性建模方法,雖然估計參數效率快,但是只能描述房地產價格的線性變化特點,無法反映房地產價格變化的隨機性,預測結果不可靠。
(2) BP神經網絡、支持向量機的房地產價格預測精度要高于多元線性回歸法的預測精度,這是因為神經網絡和支持向量機屬于非線性建模方法,可以對房地產價格隨機性變化特點進行描述,更好地把握了房地產價格的變化趨勢,然而支持向量機的建模時間太長,BP神經網絡有個別時間點的房地產價格預測誤差比較大。
(3) 本文模型的房地產價格預測精度要高于對比模型,這是由于本文模型不存在多元線性回歸法只能預測線性變化特點的局限性,同時克服神經網絡預測結果不穩定,不會出現支持向量機計算時間復雜度高的問題,且執行效率要遠遠高于支持向量機,獲得了更加理想的房地產價格預測結果。
5 結 語
房地產價格的建模與預測具有十分重要的實際應用意義,為了避免當前房地產價格預測模型存在的局限性,設計了基于數據挖掘技術的房地產價格預測模型,采用混沌理論對房地產價格數據進行預處理,確定房地產價格預測模型的輸入向量,然后采用相關向量機描述房地產價格的隨機性變化特點,最后通過仿真對比實驗結果表明,本文模型的房地產價格預測精度要高于當前其他經典的房地產價格預測模型,而且執行效率也具有一定的優勢,在房地產市場管理中具有廣泛的應用前景。
參考文獻
[1] 柳冬,王雯珺,汪壽陽.我國房地產價格影響要素分析與趨勢預測[J].經濟與金融,2011,22(5):3?11.
[2] 周海波.房地產價格影響因素的實證研究[J].海南大學學報,2009,27(5):537?543.
[3] ANUNDSEN A K, JANSEN E S. Self?reinforcing effects between housing prices and credit [J]. Journal of housing econo?mics, 2013, 22(3): 192?212.
[4] 武田艷,占建軍,嚴韋.基于MIV?BP型網絡實驗的房地產價格影響因素研究[J].數學的實踐與認識,2015,45(18):43?50.
[5] 周亮,周正.基于時間序列的房地產價格指數預測方法探討[J].哈爾濱商業大學學報(社會科學版),2008(2):80?83.
[6] 楊勵雅,邵春福.基于BP神經網絡與馬爾可夫鏈的城市軌道交通周邊房地產價格的組合預測方法[J].吉林大學學報(工學版),2008,38(3):514?519.
[7] 李萬慶,張金水,孟文清.基于小波神經網絡的房地產價格指數預測研究[J].河北工業大學學報(自然科學版),2008,25(1):74?76.
[8] 何芳,王小川,肖森予,等.基于MIV?BP型網絡實驗的房地產項目風險識別研究[J].運籌與管理,2013,22(2):229?234.
[9] 楊柳,張磊,張少勛,等.單核和多核相關向量機的比較研究[J].計算機工程,2010,36(12):195?197.
[10] 梁坤,聶會星,徐樅巍.基于支持向量機的北京市房地產價格指數預測[J].合肥工業大學學報,2011,34(4):588?592.
[11] 李大營,許偉,陳榮秋.基于粗糙集和小波神經網絡模型的房地產價格走勢預測研究[J].經濟與金融,2009,21(11):18?22.

