函數極值點偏移問題的處理策略
江西省贛州市贛縣區教師進修學校(341100) 馬躍進
函數極值點偏移問題的處理策略
江西省贛州市贛縣區教師進修學校(341100) 馬躍進
函數極值點偏移問題,是近幾年高考及各種模考題壓軸的熱點,交匯數學中函數的性質及應用、求導、方程、參數變換、不等式求解等技巧,很多學生對待此類問題經常是束手無策.而且此類問題變化多樣,題型中又含有諸多參數,更平添了求解的難度.
筆者試通過本文,給出函數極值點偏移的定義,并借助微積分的思想方法探究函數極值點偏移問題的一般性求解方法,現將有關研究寫在下面,供讀者參考.
一、極值點偏移的有關概念
首先,我們來了解函數極值點偏移的特征,并給出函數極值點偏移的定義.
1.函數極值點偏移的基本特征:是指單極值函數,由于函數極值點左右的增減速度不同,使得函數圖像沒有軸對稱性.如圖1所示.
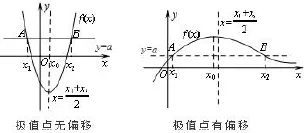
圖1
2.函數極值點偏移的定義:已知函數f(x)有唯一的極值點(x0,f(x0)),直線y=a與函數y=f(x)交于不同兩點A(x1,a),B(x2,a),設AB的中點為,若,就說函數f(x)在x=x0處的極值點有偏移.
3.函數極值點偏移的分類(已知條件如2):

圖2
構造函數F(x)=f(x0+x)-f(x0-x),x∈(-λ,λ),其中λ=|x2-x1|max(下同),易知F(x)是區間(-λ,λ)上的奇函數,以下稱F(x)為極值點偏移關聯函數.
二、極值點偏移關聯函數的應用
例1(2010天津理)已知函數f(x)=xe-x(x∈R),如果x1/=x2,且f(x2)=f(x2),證明:x1+x2>2.
解析因為 f′(x)=,易知當x< 1時, f′(x) > 0;當 x > 1時,f′(x)<0,即f(x)在(-∞,1)上單調遞增,在 (1,+∞)上單調遞減.因為函數f(x)在x=1處取得極大值f(1),且f(1)=,如圖3所示.
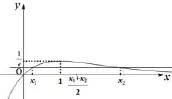
圖3
由f(x1)=f(x2),x1/=x2,不妨設x1<x2,則必有0<x1<1<x2,構造函數F(x)=f(1+x)-f(1-x),則F(x)是R上的奇函數.
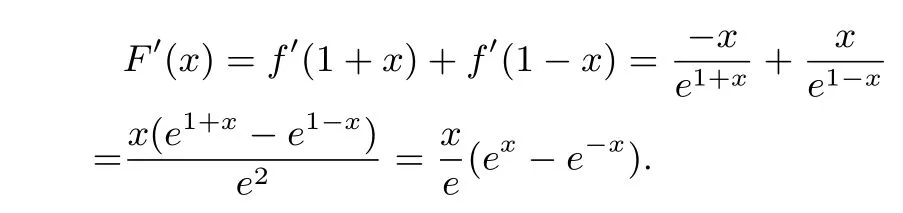
因為x=0時,F′(x)=0,x/=0時,x與ex-e-x同號,所以F′(x)≥0,即F(x)在R上單調遞增,當x∈(0,+∞)時, F(x)>F(0)=0,也即f(1+x)>f(1-x)對x∈(0,1]恒成立.由0< x1< 1< x2,則1-x1∈(0,1],所以f(1+(1-x1))=f(2-x1)>f(1-(1-x1))=f(x1)= f(x2),即f(2-x1)>f(x2),又因為2-x1,x2∈(1,+∞),且f(x)在(1,+∞)上單調遞減.故2-x1<x2,即x1+x2>2.
例2已知函數f(x)=x-aex有兩個不同的零點x1,x2,求證:x1+x2>2.
解析函數f(x)的兩個零點,等價于方程xe-x=a的兩個實根,從而這一問題與例1完全等價.
例3已知函數f(x)=lnx-ax,a為常數,若函數f(x)有兩個零點x1,x2.試證明:x1·x2>e2.
解析消參轉化成無參數問題:f(x)=0?? lnx= ax?? lnx=aelnx,x1,x2是方程f(x)=0的兩根,也是方程lnx=aelnx的兩根,則lnx1,lnx2是x=aex的兩根.設u1=lnx1,u2=lnx2,g(u)=ue-u,則g(u1)=g(u2),從而x1x2>e2?? lnx1+lnx2>2?? u1+u2>2,此問題等價轉化成為例1.
.


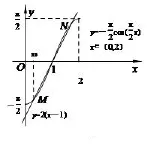
圖4
所以 x0是 f(x)在區間 (0,1)上唯一的極小值點. x1+x2>2x0?? 函數f(x)的極值點左偏.由f′(x0)=0得
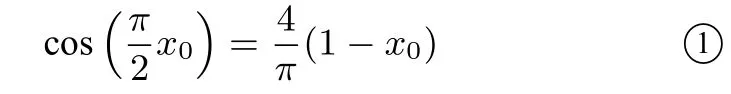
不妨設0<x1<x0<x2<1,函數f(x)極值點偏移關聯函數為F(x)=f(x0+x)-f(x0-x),x∈(-1,1),則F(x)是奇函數. ,即
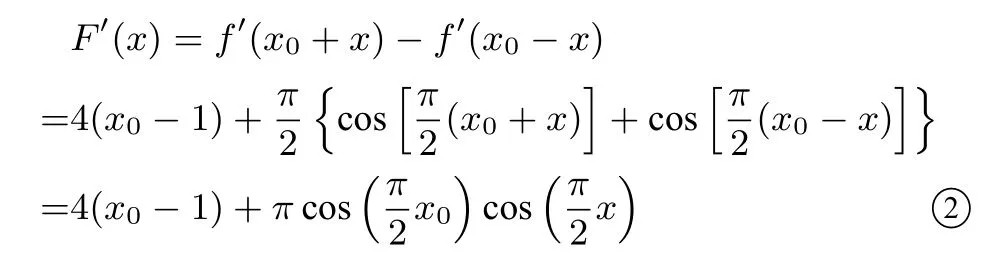
將①代入②得
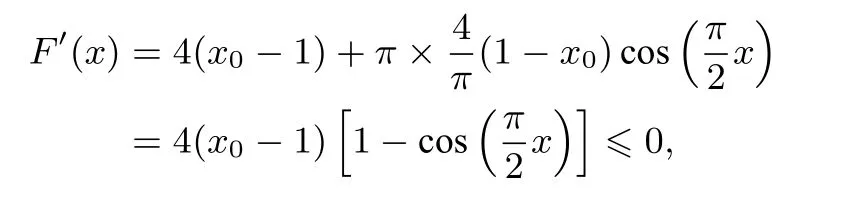
即F(x)在(-1,1)上單調遞減,當x∈(0,1)時,F(x)<F(0)=0,也即f(x0+x)<f(x0-x)在區間(0,x0]上恒成立.由0< x1< x0< x2< 1,則x0-x1∈(0,x0],所以f(x0+(x0-x1))=f(2x0-x1)<f(x0-(x0-x1))=f(x1)=f(x2),即f(2x0-x1)<f(x2),又因為2x0-x1,x2∈(x0,1),且f(x)在(x0,1)上單調遞增.故2x0-x1<x2,即x1+x2>2x0,命題得證.
例5 設函數f(x)=ex-ax+a(a∈R),其圖像與 x軸交于 A(x1,0),B(x2,0)兩點,且 x1< x2.證明:<0.

即F(x)在(-λ,λ)上單調遞增,當x∈(0,λ)時,F(x)>F(0)=0,也即f(lna+x)>f(lna-x)在區間(0,lna]上恒成立.由1<x1<lna<x2,則lna-x1∈(0,lna],所以f(lna+(lna-x1))=f(2lna-x1)>f(lna-(lnax1))=f(x1)=f(x2),即f(2lna-x1)>f(x2),又因為2lna-x1,x2∈(lna,+∞),且f(x)在(lna,+∞)上單調遞增.故2lna-x1>x2,即<lna,命題得證.


例7 (2016年新課標I卷理數壓軸21題)已知函數f(x)=(x-2)ex+a(x-1)2有兩個零點x1,x2.證明:x1+x2<2.
解析由f(x)=(x-2)ex+a(x-1)2,得f′(x)= (x-1)(ex+2a),可知f(x)在(-∞,1)上單調遞減,在(1,+∞)上單調遞增.要使函數y=f(x)有兩個零點x1,x2,則必須a>0.函數有唯一的極小值點(1,-e),所證結論為函數極值點右偏.
只需構造極值點偏移函數F(x)=f(1+x)-f(1-x),x∈R,因為
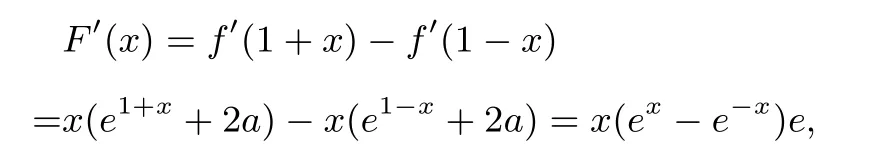
而x=0時,F′(x)=0;x/=0時,x與(ex-e-x)同號,所以F′(x)≥ 0,即F(x)在R上單調遞增.所以f(1+x)>f(1-x)在R上恒成立.不妨設x1<1<x2,則f[1+(1-x1)]>f[1-(1-x1)]=f(x1)=0=f(x2)即f(2-x1)>f(x2),又因為2-x1,x2∈(1,+∞),且f(x)在(1,+∞)上單調遞增.故2-x1>x2,即x1+x2<2.
三、函數極值點偏移問題再思考
由上述探究易知,極值點偏移取決于關聯函數F(x)=f(x0+x)-f(x0-x),x∈(-λ,λ),的單調性.而F(x)是其定義域上的奇函數,由微積分的基本性質易知F′(x)及∫F(x)dx均為區間(-λ,λ)的偶函數,都極具很好的圖形對稱性.
思考1 筆者的研究,僅僅從探究極值點偏移關聯函數F(x)的導函數F′(x)入手,得到求解極值點偏移問題的一類方法,若從研究極值點偏移關聯函數F(x)的積分函數∫F(x)dx入手,勢必可以得到求解極值點偏移問題的另類方法.
思考2 在求解極值點偏移問題時,若構造另一個關聯函數G(x)=f(x)-f(2x0-x),x∈(x0-λ,x0+λ),則函數G(x)的圖像關于點(x0,0)中心對稱,且函數G(x)的導函數G′(x)、積分函數∫G(x)dx的圖像都關于直線x=x0對稱,研究函數G(x)的單調性,也不失為求解極值點偏移問題的一種好方法.
期待對此問題感興趣的讀者,作進一步的探究.

