一道最值問題的多角度思考及教學啟示
陜西省西安中學(710018) 陳昭亮
一道最值問題的多角度思考及教學啟示
陜西省西安中學(710018) 陳昭亮
題目如圖所示,A是一座小島,海岸線上一點P的正東方向12km處是城鎮Q,AP⊥PQ, AP=2km,假設一個人駕駛的小船的平均速度為3km/h,人在海岸線上步行的速度為5km/h,試問此人從小島A出發到城鎮Q所用的最短時間是多少?
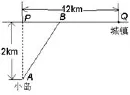
圖1
對于這道最值問題,常規的解題思路是通過建立函數模型,并求出最值.但解題時有兩個制約學生思維的“關隘”,一是要選擇合適的變元作為自變量;二是在得出函數解析式后,用什么方法求出這個函數的最值.經過筆者的研究發現,本題的解題入口寬,方法多,是考查學生靈活運用數學知識分析問題和解決問題能力的一道好題,具有較高的研究價值.本文就此題進行了多角度的思考并談幾點教學啟示.
1試題的多角度思考
思路1 本題最容易想到的是選擇線段長為自變量.設此人在海岸點B處靠岸,點B到點 P的距離BP=xkm,則BQ=(12-x)km,,又設小島到城鎮所需要的時間為t小時.則t與x間的函數關系式為,即.這是一個無理函數的最值問題,我們要想辦法把解題障礙—根號去掉,以實現問題的轉換.我們可設,這樣當y取最小值時,t最小.由得,兩邊平方整理得
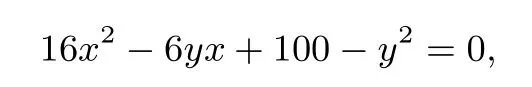
因方程有實根,所以有
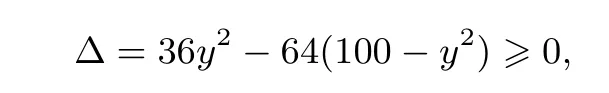

思路2 對于思路1中求無理函數
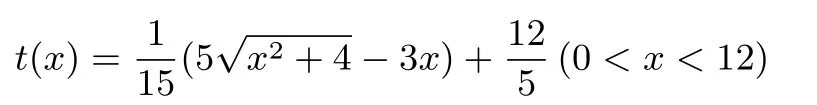
的最值這一難點,我們也可以考慮用導數的方法進行.考慮
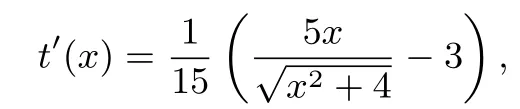
又本題在0<x<12內只有一個極值點,據題意本題有最小值,故當x=時,.下同思路1.
思路3 本題中點 B的運動,除了用思路 1中的設BP=xkm之外,我們還可以看到點B的運動也導致了∠PAB的大小變化,所以也可設∠PAB=x,則 PB=2tanx,,從而BQ=12-2tanx,故
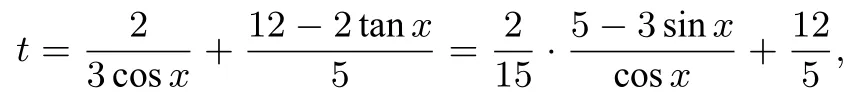

思路4對于思路3中的核心步驟求函數的最小值,觀察這個式子的結構是比值型,就聯想到斜率公式的模型,該式可看做是經過點M(-cosα,3sinα),N(0,5)的直線斜率,因為α為銳角,所以點M(-cosα,3sinα)位于橢圓落在第二象限的曲線上.
如圖2可知,當直線MN與橢圓相切時,斜率最大,又橢圓在點M(-cosα,3sinα)處的切線方程為9x(-cosα)+3ysinα=9,又因為此切線經過點N(0,5),將點N(0,5)的坐標代入得 sinα =,所以tanα=,所以PB=2tanα=時,tmin=.

圖2
2解題給我們的教學啟示
2.1 重視通性通法,淡化特殊技巧
高中數學新課程理念告訴我們:要與時俱進地認識“雙基”.我國的數學教學具有重視基礎知識教學、基本技能訓練和能力培養的傳統,新世紀的高中數學課程應發揚這種傳統.與此同時,隨著時代的發展,數學課程設置和實施應重新審視基礎知識、基本技能和能力的內涵,形成符合時代要求的新的“雙基”.因此,我們在教學中要注重通性通法,淡化特殊技巧,力求讓學生熟練掌握解決數學問題的常規方法.
思路1和2看似計算復雜,但在考試中可能是最容易想到的很自然的思路,同時,我們看到此解法也恰恰體現了試題對數學基礎知識、數學基本思想方法和運算求解能力的考查.因此,我們不能借口高考從“知識立意”轉變為“能力立意”而忽視基礎知識、基本技能和基本數學思想方法.尤其在試題的講評與訓練時,要讓學生充分體會其中蘊涵的數學思想方法,熟練掌握解決一些常規數學問題的通性通法.
2.2 強調數學本質,提升應變能力
在數學教學中,學習形式化的表達是一項基本要求,但是我們不能只限于形式化的表達,更要強調讀懂數學,其實就是強調對數學本質的認識,否則會將生動活潑的數學思維活動淹沒在形式化的海洋里.此題如果學生能清晰地理解解析幾何的本質,那么想到思路4的也就顯得很自然.數學是一門思維的學科,學生只有在思維的過程中才能加深對數學本質的理解.我們的教學如何才能以不變應萬變,這就要求我們在教學中要充分揭示數學思維的全過程,培養學生的理性思維,引導學生關注題后的反思和拓展,強調數學本質,以提升學生的思維品質.
2.3 關注知識交匯,提升綜合能力
思路3當看到點B的運動,也導致了∠PAB的大小變化,所以設∠PAB=x,從而把問題轉為三角函數的最值問題.真是聯想豐富,解法有創意.近年來體現在數學知識交匯處的試題經常出現,這類題目對學生綜合運用數學知識解決問題的能力要求較高.例如,我們把代數中求函數值域的問題可以轉化到幾何中求距離或斜率的問題;幾何中的距離或最值問題也可以通過三角問題或函數的知識來解決;立體幾何中空間角、距離可以通過空間向量的方法來解決;解析幾何常常與平面向量結合在一起.所有這些都體現了數學中各個分支其實是一個有機的整體.因此,我們在教學中要重視設計知識交匯處的例習題,充分挖掘知識點的內涵,通過變換條件、結論來設計一題多變、一題多問、一題多解,創設開放性數學情境,引導學生發揮聯想,從多角度、多維度去考察問題,提高學生分析和解決問題的能力.
2.4 突出數學思想,提升數學素養
高中數學新課程標準告訴我們:“數學教學要體現課程改革的基本理念,在教學中要引導學生積極主動地學習,掌握數學的基礎知識和基本技能以及它們所體現的數學思想方法,發展應用意識和創新意識,對數學有較為全面的認識,提高數學素養.”數學教學的根本目的是培養學生的數學思想,提升學生的數學素養,通過數學學習,使學生能用數學的思考方式去觀察問題、分析問題和數學地解決問題.

