耦合水力約束的成品油管道調度模型研究

段志剛，梁永圖，張浩然，顏筱函，廖綺

中國石油大學(北京)城市油氣輸配技術北京市重點實驗室, 北京 102249

耦合水力約束的成品油管道調度模型研究

段志剛，梁永圖*，張浩然，顏筱函，廖綺

中國石油大學(北京)城市油氣輸配技術北京市重點實驗室, 北京 102249

成品油管道系統能否經濟、高效地運行，關鍵在于運營單位編制與執行調度計劃的水平。由于成品油管道是一個復雜的密閉水力系統，僅約束流量難以保證管道總體運行達到最優。當前，國內外學者針對成品油管道調度優化問題展開大量的研究，但少有研究將水力約束耦合在內。本文以調度周期內體積總偏差最小為目標函數，綜合考慮了注入、分輸、泵站、批次運移、水力等約束，建立了連續時間的混合整數非線性規劃(MINLP)模型，并將其分解成整數規劃(IP)問題及混合整數線性規劃(MILP)問題求解。而后，利用提出的優化模型求解出某條成品油管道的具體優化調度方案和啟泵方案。調度周期為179.7 h，計算時間180.32 s。調度計劃滿足現場需求，結果表明模型實用、高效。

成品油管道；水力耦合；調度優化；混合整數非線性規劃；啟泵方案

0 引言

截止2014年底，全球成品油管道里程已達26.7×105km[1]。在如此龐大的管道規模下，管道調度的重要性就更為凸顯。成品油管道系統能否經濟、高效地運行，關鍵在于運營單位編制與執行調度計劃的水平。多批次成品油管道調度問題是針對多批次輸送的運行模式，根據煉廠生產計劃及下游市場的需求計劃，制定出管道的整體調度計劃。高效確定各源點的注入計劃、各下載站的下載計劃、各泵站的啟泵方案以及最小運行成本是管道調度優化的實質所在[2]。

Rejowski等[3-4]建立了首站向5個分輸站輸送4種油品的離散時間MILP模型。由于存在大量的二進制變量，模型求解時間較長。隨后，Rejowski等[5]和Cafaro等[6-8]分別提出了基于連續時間的MINLP和MILP模型。模型采用較少的二進制變量和約束條件，使得求解速度大幅度提高。Cafaro和Cerda[9]提出多源單匯管網調度的MILP模型，該模型考慮了多個注入站同時注入油品的情形。而后Mirhassani等[10]、Cafaro[11]等在建立多源單匯管網的模型時考慮了能耗問題。MirHassani和Jahromi[12]、Cafaro和Cerda[13]對單源多匯管網提出連續時間MILP方法，不同的是前者假設支線只能輸送一種油品，后者允許不同的油品進入支線。Zhang等人[14]提出了一種混合算法求解基于供給的單源多匯成品油管道調度優化問題，算法可以求解出詳細的調度計劃。后來Zhang等人[15]基于之前的研究，考慮了多泵站工藝約束，采用一種兩階段算法對模型進行求解。雖然前人對成品油管道調度優化進行了大量的研究，但是很少研究對水力約束進行詳細討論，多是把壓力約束規約于流量約束進行考慮，規約的流量范圍相對保守，不能使管道運行達到最優。本文綜合考慮批次運移、注入、分輸等約束建立了耦合水力的成品油管道批次調度優化MINLP模型。采用混合算法對模型進行求解，得出最終注入及下載方案。

1 模型建立

本文設i∈I為站場編號的集合；j∈J為批次編號的集合；l∈L為油品編號的集合；tc∈TC為時間節點編號的集合；pa∈PA為節點壓力的集合。

1.1 模型假設

(1) 假設輸送的油品是不可壓縮流體，即體積不隨溫度和壓力變化；

(2) 假設混油批次為一個界面。

1.2 目標函數

模型以各站的實際下載量與需求量偏差之和最小為目標函數。存在偏差時，分2種情況：下載量大于需求量或下載量小于需求量。各站的重要程度不同，產生偏差所造成的損失也不同。

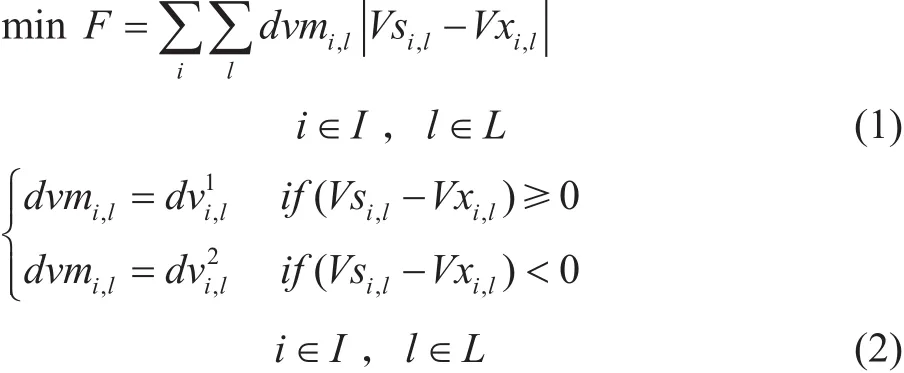
其中：dvmi,l為i站對l油品需求與實際下載偏差造成的損失單價，CNY/m3；為i站對l油品過量下載造成的損失單價，CNY/m3；為i站實際下載未能滿足對l油品需求造成的損失單價，CNY/m3；Vxi,l為i站對l油品需求體積，m3；Vsi,l為i站對l油品實際的下載體積，m3。

1.3 約束條件

1.3.1 分輸約束

各個站場下載油品的總量為實際下載量。

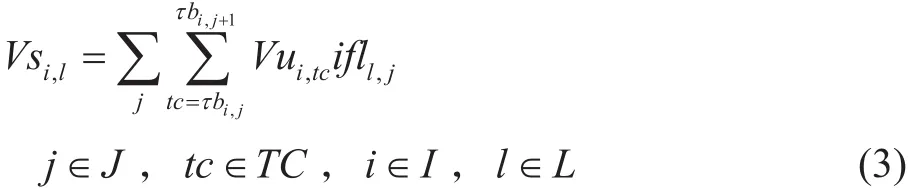
其中：τbi,j為j批次油頭到達i站時間點編號；Vui,tc為i站在tc時間點到tc+1時間點之間的下載體積，m3；ifll,j為油品類型二元參數，若j批次輸送l油品則fll,j=1，否則fll,j=0。

每個站的下載流量不能大于該時刻前一段管道內的流量，且下載不同油品的流量上限也不同。

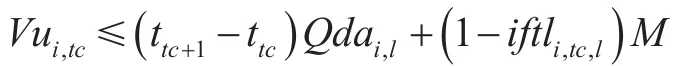
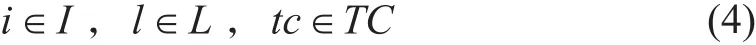
其中：Qdai,l為i站下載l油品的流量上限，m3/h；iftli,tc,l為下載油品二元變量，若i站tc時間點到tc+1時間點之間下載l油品則iftli,tc,l=1，否則iftli,tc,l=0；M為極大值，其他變量同前。

過站油品是該站場需求的油品，且該批次油頭已到達該站場，則站場可以下載該批次油品。

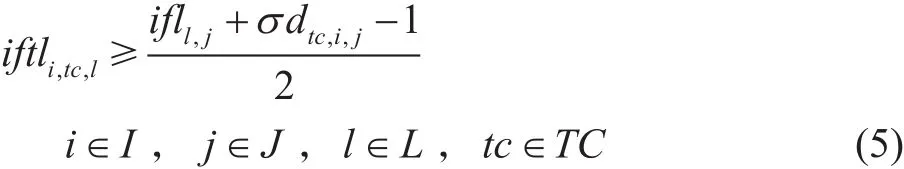
其中：σdtc,i,j為批次到站二元變量，若j批次tc時間點到達i站則σdtc,i,j=1，否則σdtc,i,j=0；其他變量同前。

一個站場在同一時間窗內最多只能下載一種油品。

式中變量同前。

1.3.2 批次運移約束

過站流量需大于管段內允許的最小流量。當管段中不存在混油界面時，其最小流量根據泵機組以及計量設備限制決定，稱此流量約束為設備流量下限約束。考慮到混油擴散的問題，當管段中存在批次界面時，需要保證管段雷諾數大于臨界雷諾數，稱此流量約束為混油流量下限約束。

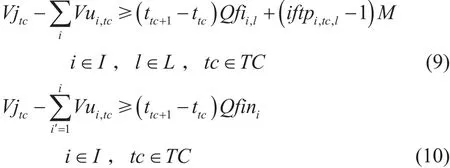
其中：Vjtc為tc時間點到tc+1時間點首站注入體積，m3；Qfii,l為l油品油頭在i站到i+1站之間管道時的流量下限，m3；iftpi,tc,l為油頭運移二元變量，若在tc時間點與tc+1時間點之間i站到i+1站存在輸送l油品批次油頭，iftpi,tc,l=1，否則iftpi,tc,l=0；Qfini為i站到i+1站之間的管道流量下限，m3/h；其他變量同前。

考慮到泵機組以及計量設備約束，管段流量應小于管段允許的流量上限。式(11)為i～i+1管段存在批次界面的情況；式(12)為i～i+1管段不存在批次界面的情況。

其中：Qfai,l為l油品的批次油頭在i站到i+1站之間管段時的流量上限，m3/h；；Qfani為i站到i+1站之間管段的流量上限，m3/h；其他變量同前。

如果批次界面位于管段起終點之間，則該管段內存在批次界面。

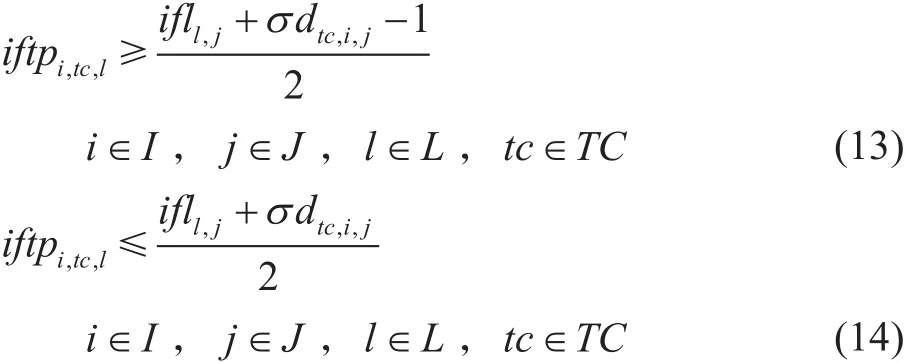
式中變量同前。

根據體積守恒原則，首站注入量等于沿線所有站場下載量之和。

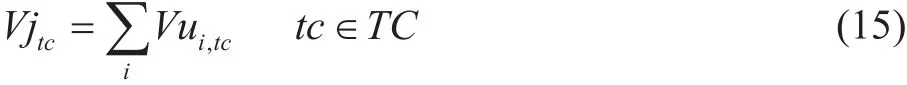
式中變量同前。

油品在管道中的位置用體積坐標的形式表示。

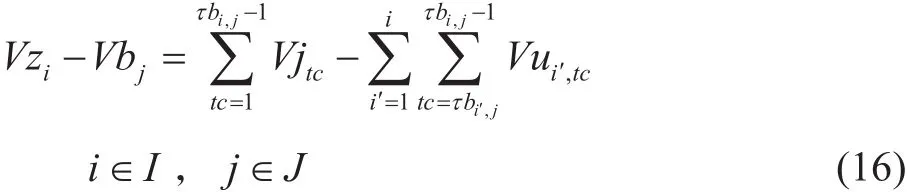
其中：Vzi為i站站場的體積坐標，m3；Vbj為j批次注入體積，m3；其他變量同前。

1.3.3 注入約束

在一定的時間內，首站的注入體積應小于該時段的流量上限與時長的乘積。

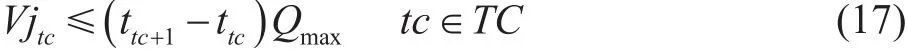
其中：Qmax為首站注入流量上限，m3/h；其它變量同前。

在一定的時間內，首站的注入體積應大于該時段的流量下限與時長的乘積。

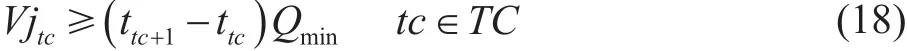
其中：Qmin為首站注入流量下限，m3/h；其他變量同前。

批次在首站的注入體積應等于注入該批次的時間節點到下一個注入批次油頭的時間節點之間的注入總體積。

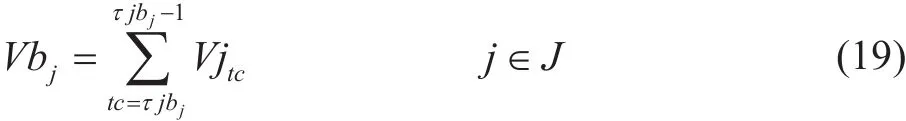
式中變量同前。

新批次的體積坐標等于該批次研究的開始時刻到注入該批次開始時刻之間首站注入總體積的負值。其中：Vbnew為新注入批次的體積坐標，m3；其他變量同前。

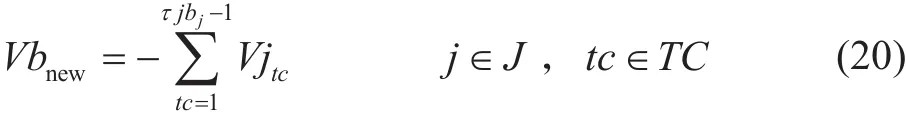
1.3.4 水力約束

泵站提供的壓能要克服沿程摩阻及高程差。同時，管道各個節點也應滿足水力約束，即油品到達泵站時，入口壓力需大于泵站的最小進站壓力。式(21)為站間存在批次界面時的表達式，式(22)為站間不存在批次界面時的表達式。

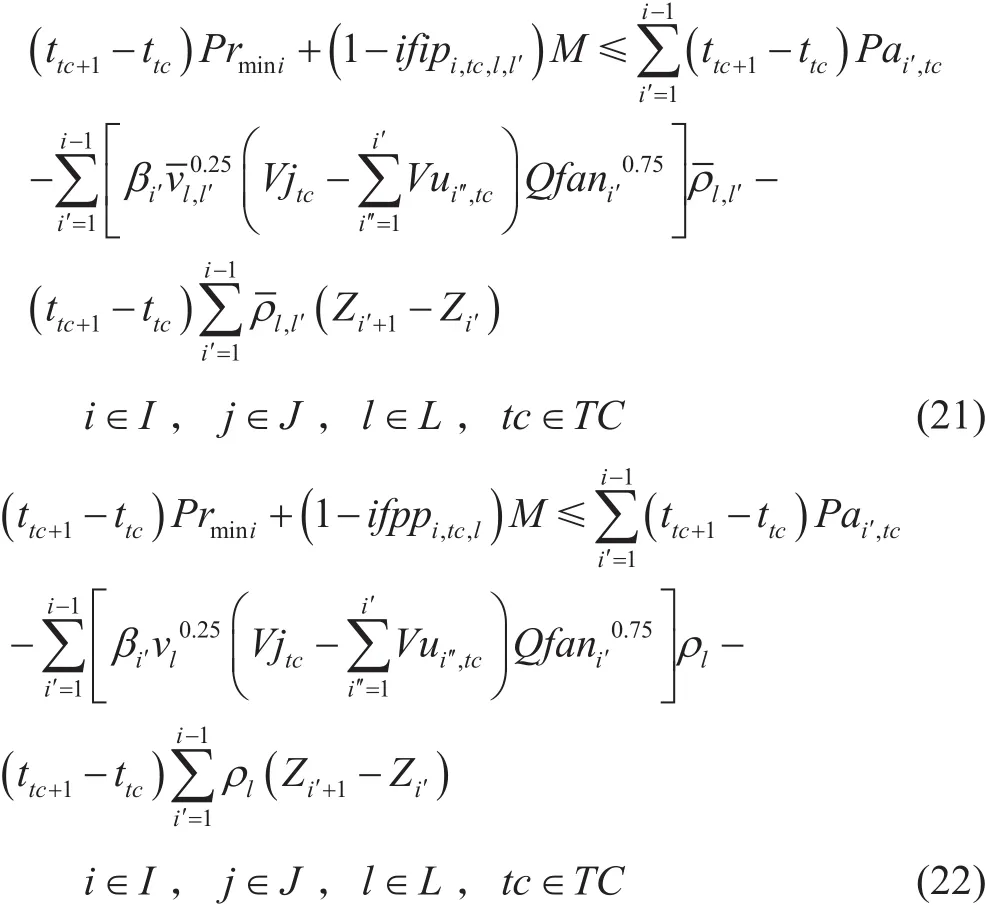
其中：Prmini為i站最小進站壓力，Pa；ifipi,tc,l,l′為混油運移二元變量，若tc時間點到tc+1時間點之間i站到i+1站之間存在l油品與l'油品混油，ifipi,tc,l,l′=1，否則ifipi,tc,l,l′=0。ifppi,tc,l為站間充滿單一油品的二元變量，若tc時間點到tc+1時間點之間i站到i+1站之間充滿l油品則ifppi,tc,l=1，否則ifppi,tc,l=0；βi′為列賓宗摩阻計算系數；Zi為i站高程，m；為l油品與l'油品的平均黏度，Pa· s；為l油品與l'油品的平均密度，kg/m3；υl為l油品的平均黏度，Pa· s；ρl為l油品的平均密度，kg/m3；Pai,tc為i站tc時間點到tc+1時間點之間時刻提供的壓力，Pa；其它變量同前。

站間存在批次界面時，混油運移二元變量滿足如下約束。

2 模型求解

由于本模型屬于大規模復雜MINLP模型，直接求解非常困難。考慮到模型中二元變量之間的耦合性強于二元變量與連續變量的耦合性，故本文將與時間相關的二元變量從模型中抽離出來，用蟻群算法求解得到與時間相關的二元變量，將非線性約束線性化，從而求得調度方案。根據批次界面位置和管道流量計算各個時刻管段的沿程摩阻。然后綜合考慮各泵機組參數、進出站壓力、管段壓力、泵啟停時間等計算最優啟泵方案。具體求解步驟如下：

Step 1輸入管道信息、初始狀態管道內油品信息、首站注入需求、分輸站分輸需求以及泵站等信息。

Step 2將MINLP模型中的二元變量抽離出來組合成新的IP子問題。假設所有中間站場均不進行下載操作，由此可確定一組事件發生的時間節點排序，從而求得一組二元變量的解，并將此解作為蟻群算法的初始解。

Step 3將IP子問題的解帶入原MINLP模型，即可得到原模型的一組解。

Step 4判斷原目標函數的偏差是否滿意。若滿意，則開始Step 5計算摩阻。若不滿意則返回Step 2調整時間節點排序。

Step 5基于Step 4中求得的調度計劃計算各個時刻管段的沿程摩阻。

Step 6依據沿程摩阻和高程差以及泵站信息確定開泵方案。

Step 7判斷開泵方案是否可行。若可行，則輸出調度方案及開泵方案。若不可行則返回Step 2，重新迭代。

用蟻群算法調整二元變量的策略：將各時間節點順序對應的目標函數值作為螞蟻對應的信息濃度值，按濃度值對相應數量的螞蟻進行位置更新，并解碼出新的時間節點順序，直到滿足收斂條件。程序框圖如圖1所示。

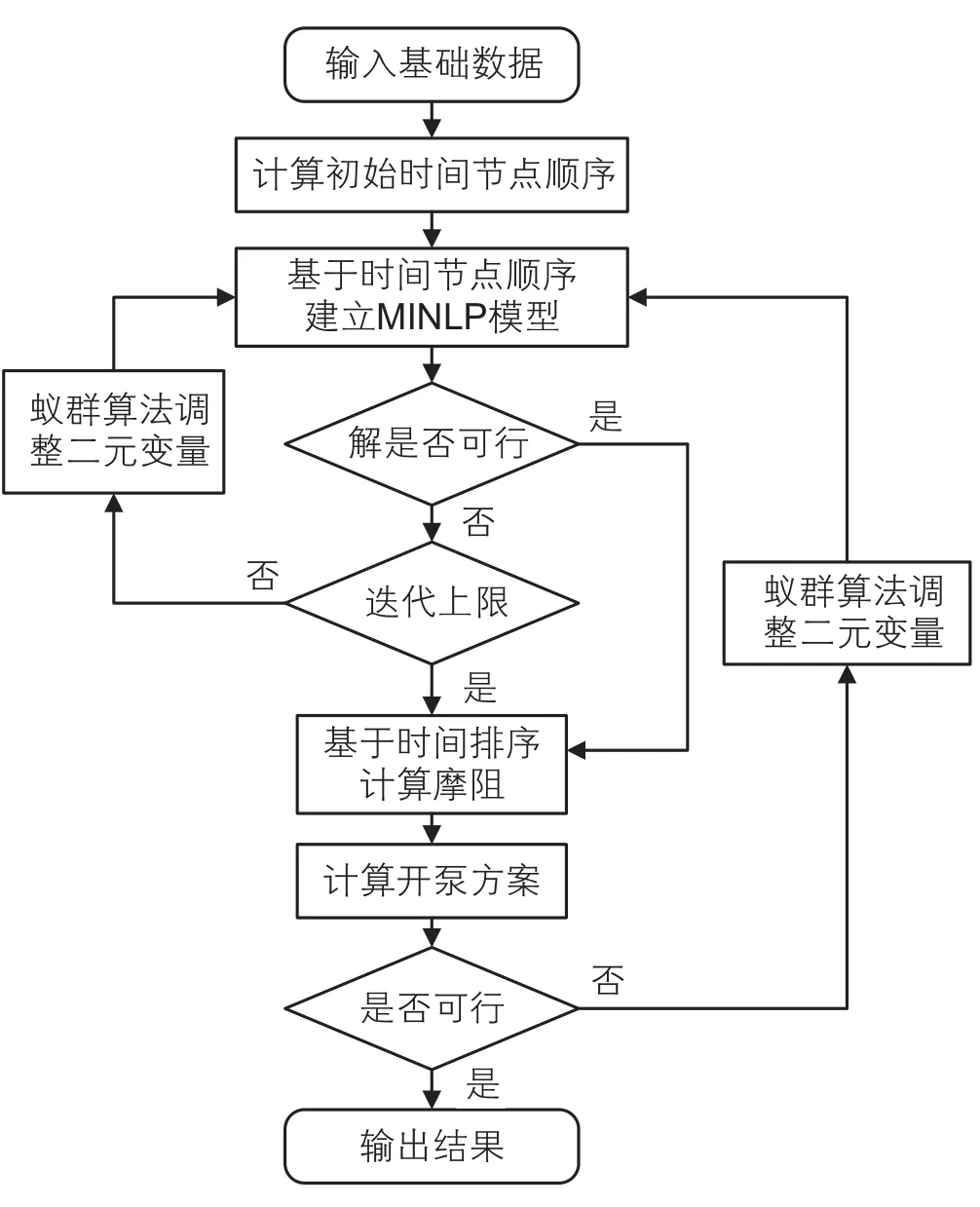
圖1 算法程序框圖Fig. 1 Flow chart of algorithm

3 算例

3.1 管道基礎數據及工藝

本文以我國某條成品油管道為例，該管道包含SS、SX、YW、JH、LY五個站。各站具體信息如圖2所示。該管道以滿足市場需求為首要任務，在滿足關鍵節點壓力的情況下，實現能耗最低。為了避免過多的節流能耗浪費，需要控制管道末站進站壓力小于一允許值。各中間下載站不允許下載混油，規定在批次到站前后半小時內不允許執行下載操作。本問題的目標就是在已知各站需求量的情況下求解出滿足所有約束的調度計劃及開泵方案。算例周期設為179.7 h，共輸送3種油品，共分為5個批次。

泵站信息：沿線共有2個分輸泵站，泵的揚程和流量的關系為H=-AQ2+BQ+C，系數如表1所示。

初始時刻管道完全被0#柴油填充，體積為管道的管存67 139 m3。所輸送的0#柴油密度為845 kg/m3，92#汽油密度為740 kg/m3，95#汽油密度為750 kg/m3。調度周期內需要輸送的批次和計劃輸送量見表2。

調度周期內，各個站場需求量見表3。

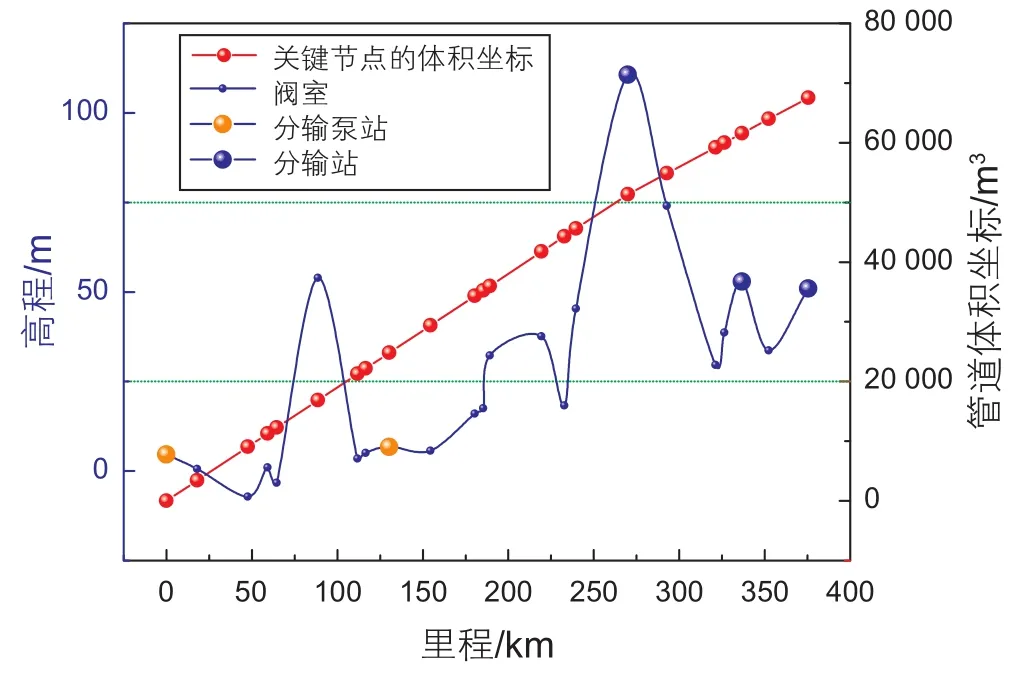
圖2 管線縱斷面圖Fig. 2 The pro fi le of the pipeline

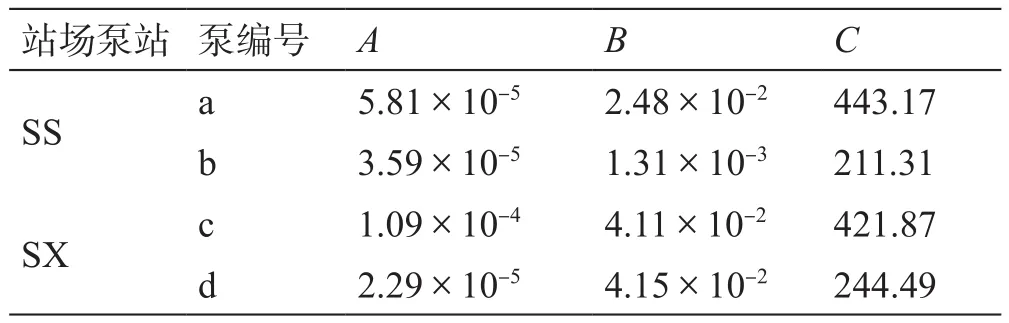
表1 揚程和流量系數Table 1 Coef fi cient of pump head and fl owrate

表2 首站輸送任務Table 2 Transportation task at the initial station

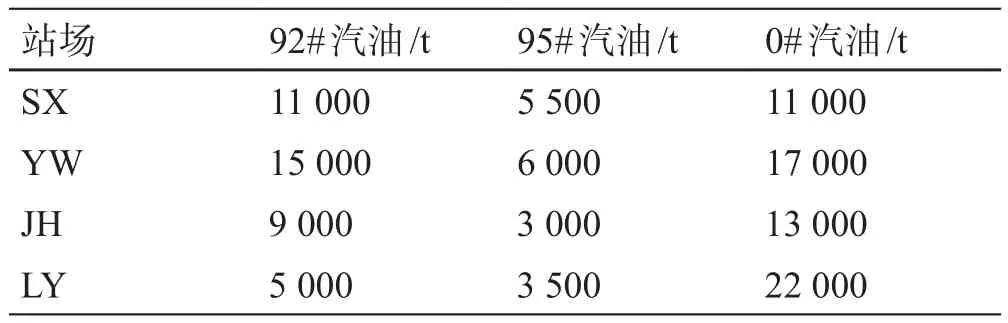
表3 分輸站需求Table 3 Demand at delivery stations

3.2 結果輸出

本模型IP子模型采用MATLAB編程求解，MILP子模型采用Gurobi線性求解器進行求解。總計算時間為180.32 s。各站詳細的分輸、注入計劃如圖3所示。圖中縱軸表示體積坐標，橫軸表示時間。黑色實線表示混油界面運移過程，其斜率表示混油界面流量。圖中處于首站體積坐標處的矩形表示注入操作，處于分輸站體積坐標處的矩形表示該分輸站的下載操作。左側縱向的矩形表示管道初始狀態。橫向矩形的顏色表示油品的種類，矩形的寬度表示操作流量。其中，紅色表示0#柴油，藍色表示92#汽油，橙色表示95#汽油。

詳細開泵方案如圖4所示，圖中實線表示泵處于開啟狀態。

在SX站處，進、出口均滿足管道壓力約束。YW站場位于高點處，該點壓力始終大于油品的飽和蒸汽壓。調度周期內SX站和YW站壓力變化如圖5所示。

各站完成輸送任務明細見表4。偏差占輸送任務的0.5‰。

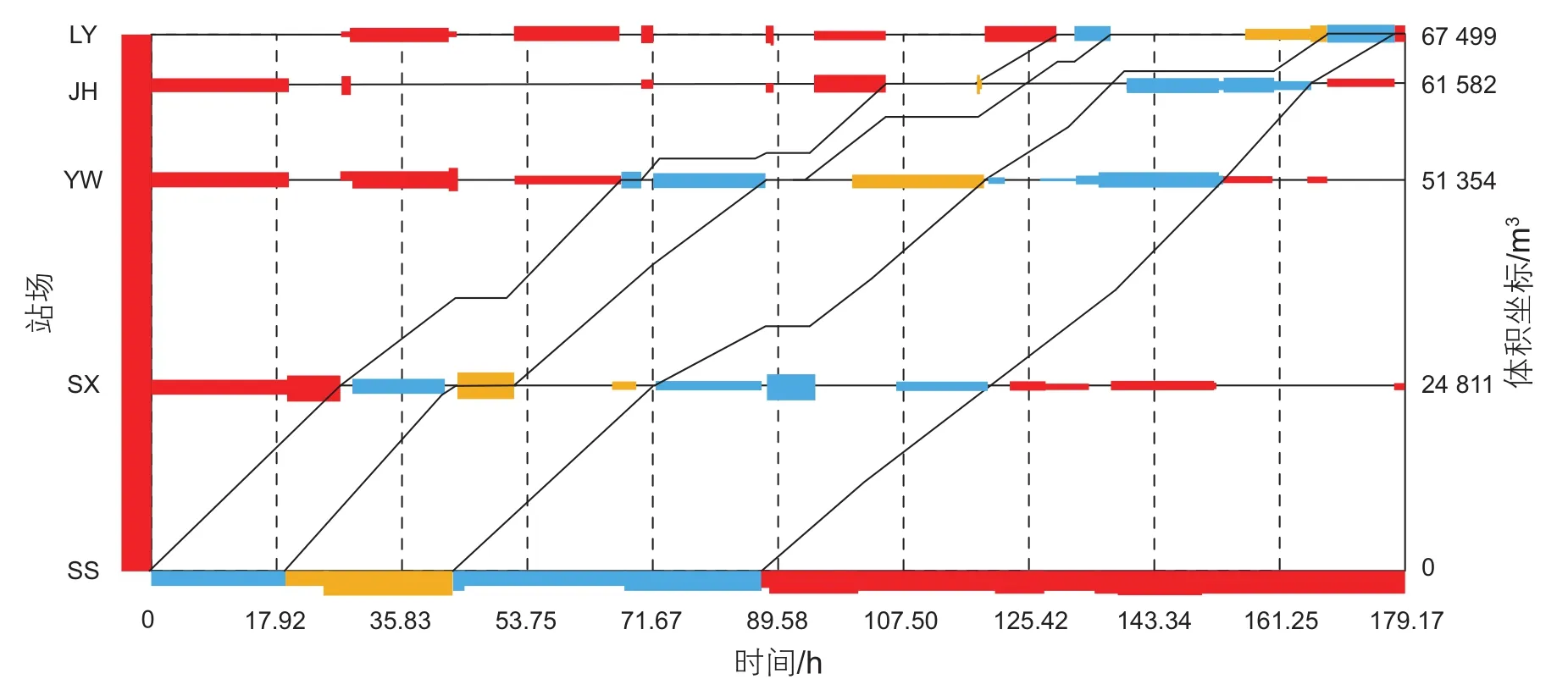
圖3 批次運移圖Fig. 3 Batch migration

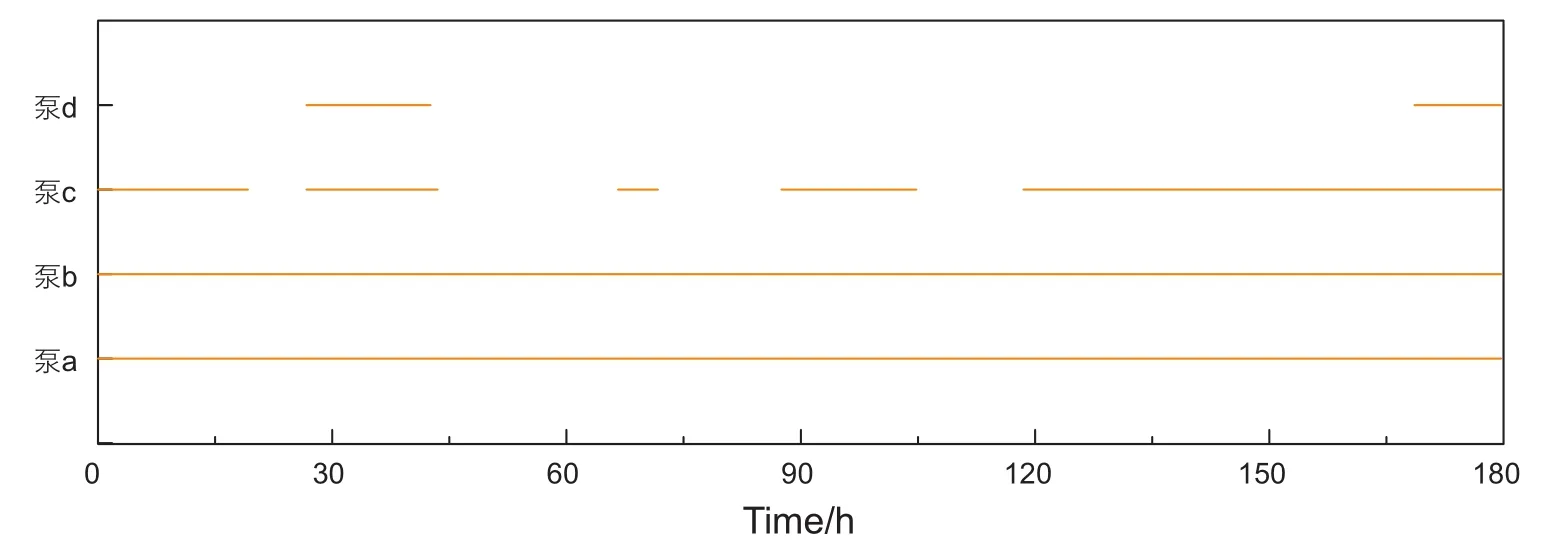
圖4 開泵方案示意圖Fig. 4 Pumping plan

4 結論

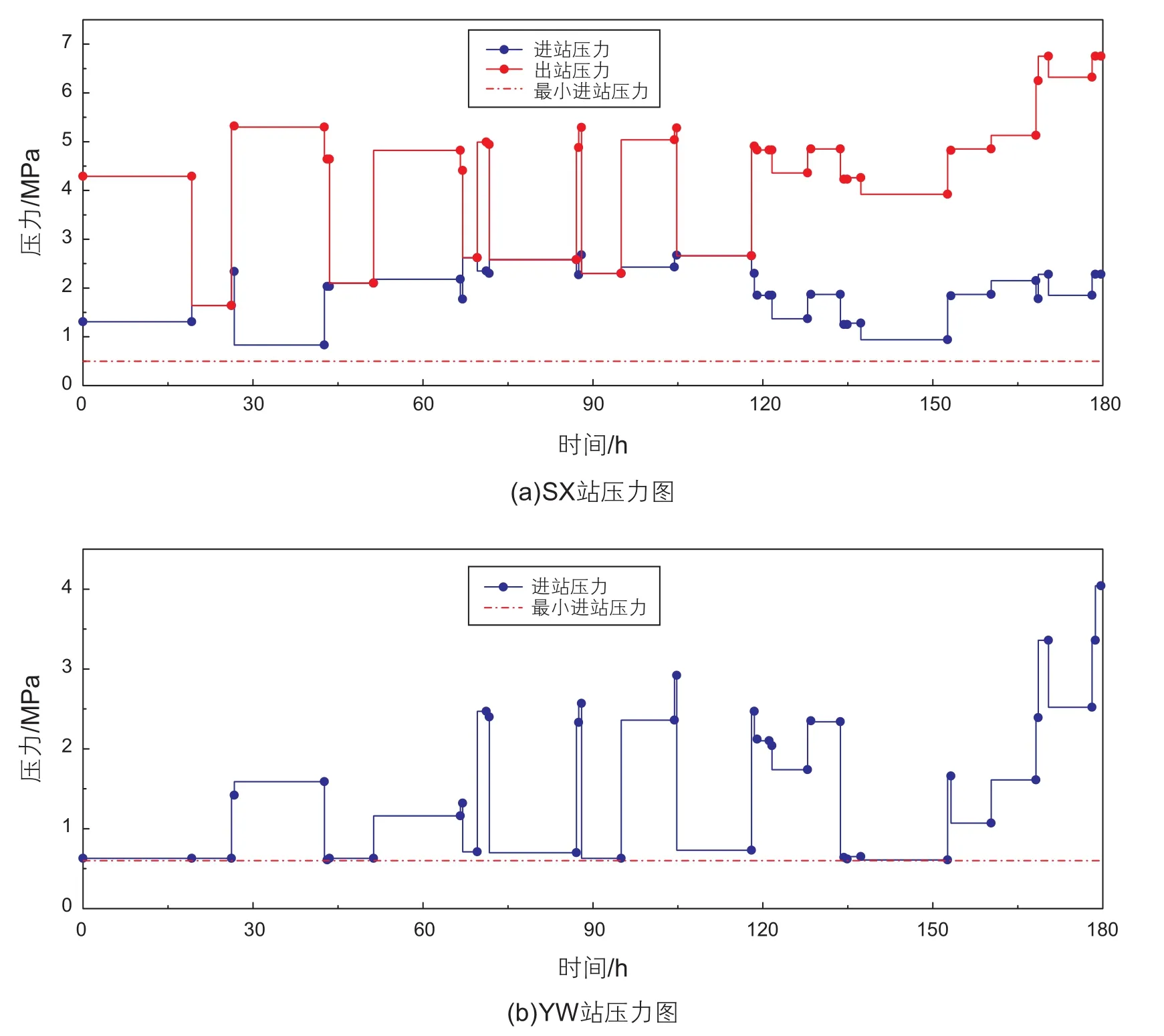
圖5 關鍵站場壓力變化示意圖Fig. 5 Pressure fl uctuation at each stations

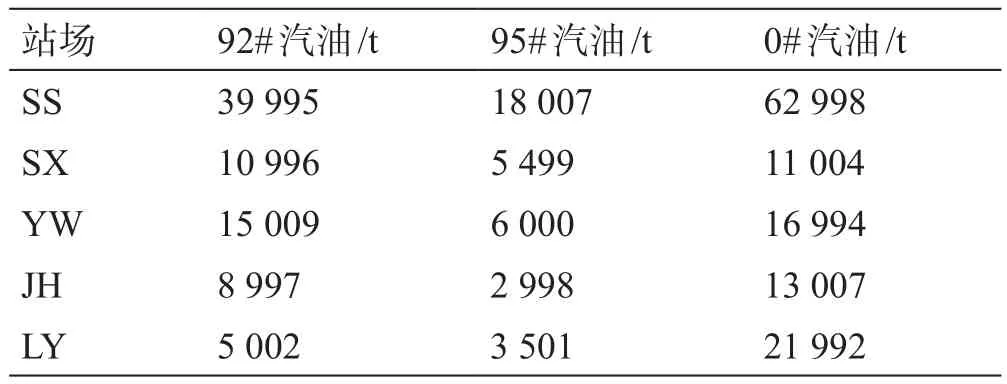
表4 輸送任務完成表Table 4 Execution results of the transportation task

本文介紹了一種耦合水力的成品油調度方法。該模型考慮了注入、分輸、批次運移以及水力約束。模型求解時，將復雜的MINLP模型分解成較為容易的IP規劃和MILP規劃，較大地提高了求解速度。本文以某條成品油管道為研究對象，調度周期為179.7 h。計算出的調度計劃、開泵方案、以及工況改變時各站的壓力滿足現場需求。手工編制該調度計劃通常需要4～5 h，偏差為5%左右。本方法僅用時180.32 s，可將偏差控制在0.5‰左右。本模型從全局角度權衡各分輸站的油品需求，制定的調度計劃實際下載量與計劃量偏差較小。

[1] 趙忠德, 焦中良, 田瑛, 等. 國外成品油管道發展現狀、發展趨勢及啟示[J]. 石油規劃設計, 2016, 27(4): 7-9.[ZHAO Z D, JIAO Z L, TIAN Y, et al. Development situation, development trend and enlightenment of foreign product oil pipelines[J]. Petroleum Planning & Engineering, 2016, 27(4): 7-9.]

[2] 梁永圖, 張浩然, 邵奇. 成品油管網調度優化研究進展[J]. 油氣儲運, 2015, 34(7): 685-688.[LIANG Y T, ZHANG H R, SHAO Q. Progress in the study on scheduling optimization of products pipeline network[J]. Oil & Gas Storage and Transportation, 2015, 34(7): 685-688.]

[3] JR R R, PINTO J M. Scheduling of a multiproduct pipeline system[J]. Computers & Chemical Engineering, 2003, 27(8): 1229-1246.

[4] JR R R, PINTO J M. Efficient MILP formulations and valid cuts for multiproduct pipeline scheduling[J]. Computers & ChemicalEngineering, 2004, 28(8): 1511-1528.

[5] JR R R, PINTO J M. A novel continuous time representation for the scheduling of pipeline systems with pumping yield rate constraints[J]. Computers & Chemical Engineering, 2008, 32(4): 1042-1066.

[6] CAFARO D C, CERDá J. Optimal scheduling of multiproduct pipeline systems using a non-discrete MILP formulation[J]. Computers & Chemical Engineering, 2004, 28(10): 2053-2068.

[7] CAFARO D C, CERDá J. Dynamic scheduling of multiproduct pipelines with multiple delivery due dates[J]. Computers & Chemical Engineering, 2008, 32(4): 728-753.

[8] CAFARO D C, CERDá J. Optimal scheduling of re fi ned products pipelines with multiple sources[J]. Industrial & Engineering Chemistry Research, 2009, 48(14): 6675-6689.

[9] CAFARO D C, CERDá J. Operational scheduling of refined products pipeline networks with simultaneous batch injections[J]. Computers & Chemical Engineering, 2010, 34(10): 1687-1704.

[10] MIRHASSANI S A, ABBASI M, MORADI S. Operational scheduling of re fi ned product pipeline with dual purpose depots[J]. Applied Mathematical Modelling, 2013, 37(8): 5723-5742.

[11] CAFARO D C, CERDá J. Rigorous scheduling of mesh-structure refined petroleum pipeline networks[J]. Computers & Chemical Engineering, 2012, 38(5): 185-203.

[12] MIRHASSANI S A, FANI JAHROMI H. Scheduling multi-product tree-structure pipelines[J]. Computers & Chemical Engineering, 2011, 35(1): 165-176.

[13] CAFARO D C, CERDá J. A rigorous mathematical formulation for the scheduling of tree-structure pipeline networks[J]. Industrial & Engineering Chemistry Research, 2010, 50(9): 5064-5085.

[14] ZHANG H R, LIANG Y T, XIAO Q, et al. Supply-based optimal scheduling of oil product pipelines[J]. Petroleum Science, 2016, 13(2): 355-67.

[15] ZHANG H R, LIANG Y T, LIAO Q, et al. A hybrid computational approach for detailed scheduling of products in a pipeline with multiple pump stations[J]. Energy, 2016.

A multi-product pipeline scheduling model coupled with hydraulic constraints

DUAN Zhigang, LIANG Yongtu, ZHANG Haoran, YAN Xiaohan, LIAO Qi
Beijing Key Laboratory of Urban oil and Gas Distribution Technology ,China University of Petroleum-Beijing, Beijing, 102249, China

The economic and efficient operation of multi-product pipelines is crucially determined by preparing and implementing scheduling plans in operating units. Considering the multi-product pipeline is a complicated closed hydraulic system, the fl owrate constraints alone cannot guarantee the optimization for overall pipeline operation. At present, domestic and foreign scholars are undertaking a lot of research into scheduling optimization for multi-product pipelines while mostly neglecting hydraulic constraints. In this paper, an objective function is established to minimize the total volume deviation in scheduling periods, comprehensively considering the injection, delivery, pump stations, batch migration and hydraulic constraints. A continuous-time mixed integer nonlinear programming (MINLP) model is put forward and solved by decomposing the model into integer programming (IP) and mixed integer linear programming (MILP) issues. Moreover, the proposed optimization model is put into practice for a real-world multi-product pipeline and works out the detailed optimal scheduling plan and pumping plan accordingly. Results show that the scheduling period is 179.7 hours and the calculation time is 180.32 seconds. The scheduling plan can be compliant with fi eld requirements, which indicates the ef fi ciency and reliability of the model.

multi-product pipeline; hydraulic coupling; scheduling optimization; MINLP; pumping plan

10.3969/j.issn.2096-1693.2017.01.011

(編輯 馬桂霞)

*通信作者, liangyt21st@163.com

2016-12-12

國家自然科學基金(No.51474228)資助

段志剛, 梁永圖, 張浩然, 顏筱函, 廖綺. 耦合水力約束的成品油管道調度模型研究. 石油科學通報, 2017, 01: 115-122

DUAN Zhigang, LIANG Yongtu, ZHANG Haoran, YAN Xiaohan, LIAO Qi. A multi-product pipeline scheduling model coupled with hydraulic constraints. Petroleum Science Bulletin, 2017, 01: 115-122. doi: 10.3969/j.issn.2096-1693.2017.01.011