粗糙集理論在數據分析中的應用研究

高亮

（安徽國際商務職業學院，安徽合肥230051）

粗糙集理論在數據分析中的應用研究

高亮

（安徽國際商務職業學院，安徽合肥230051）

隨著Internet、信息檢索等新技術的不斷出現及快速發展，各種應用所積累的數據量急劇增長，如何從這些海量數據中提取有用的信息成為了一個很現實而且重要的問題.本文結合實例分析，給出了基于粗糙集理論數據分析的一般過程，為數據挖掘提供了一個新的方法.

粗糙集；數據分析；屬性

1 引言

當今世界正處在一個數據爆炸的時代.伴隨著多媒體、云計算、物聯網、社交網絡等技術的發展，以及天文觀測、空間地理、金融分析等各領域每天都在產生巨量的數據，然而面對著這一片紛繁復雜的數據，就像面對著一個巨大的礦脈，怎樣才能從中挖掘出真正的“金子”？那么最重要便是數據挖掘的工作，所謂數據挖掘就是從大量的、不完全的、有噪聲的、模糊的、隨機的數據中，提取隱含在其中的、事先不知道的、但又是潛在有用的知識和信息的過程.目前，數據挖掘在科學研究、市場營銷金融市場分析和預測、醫療保健、教育教學等許多領域得到了廣泛的應用，已經成為計算機科學與工程研究的一個熱點.

然而，實際系統中的數據一般都具有不完全性、冗余性和模糊性，很少能直接滿足數據挖掘算法的要求，嚴重影響了數據挖掘算法的執行效率.而粗糙集理論是一種用于處理不確定性和含糊性知識的數學工具，目前在數據挖掘的各方面已有很好的應用，其基本思想是在保持分類能力不變的前提下，通過知識約簡，導出概念的分類規則.它無需提供相關數據集合外的任何先驗信息，適合于發現數據中隱含的、潛在有用的規律，即知識，找出其內部數據的關聯關系和特征.

2 粗糙集相關理論

粗糙集(Rough Set)理論是波蘭數學家Z.pawlak于1982年提出的，是一種新的處理含糊性和不確定性問題的數學工具.相對于概率統計、模糊集等處理含糊性和不確定性的數學工具而言，粗糙集理論有這些理論不具備的優越性.統計學需要概率分布，模糊集理論需要隸屬函數，而粗糙集理論的主要優勢就在于它不需要關于數據的任何預備的或額外的信息.現已廣泛應用于知識發現、機器學習、決策支持、專家系統等領域.

定義1[1]設U是一個論域，R是U上的一個等價關系，U/R表示R的所有的等價類（或者U上的分類）構成的集合，[x]R表示包含元素x∈U的R等價類.一個知識庫就是一個關系系統K=(U,R)，其中U為非空有限集，稱為論域，R是U上的一簇等價關系.若P?R，且P≠?，則∩P（P中所有等價關系的交集）也是一個等價關系，稱為P上的不可區分關系，記為IND(P)，且有.

定義2[1]設集合X?U，R是一個等價關系，稱，且[x]R?}為集合X的R下近似集；稱，且[x]R∩X≠?}為集合X的R上近似集.稱集合為X的R邊界域；稱為X的R正域；稱為 X的R負域.

定義3[2]四元組S=(U,A,V,F)是一個信息系統，其中U為對象非空的有限集合，稱為論域，即U={x1,x2,…,xn}；A=C∪D是有限屬性集合，A={a1,a2,…,am},子集C和D分別稱為條件屬性和決策屬性；

定義4[3]S=(U,A,V,F)是一個信息系統，A=C∪ D，設P，Q?A，當時，稱知識Q是k度依賴于知識P，記P?kQ，即對象的k×100%可以通過知識P劃分到U/P的模塊中.當k=1時，稱屬性集Q完全依賴于P；0＜k＜1時，稱屬性集Q部分依賴于P；k=0時，稱屬性集Q完全獨立于P；而屬性子集P?C關于D的重要性定義為σ(P)=rC(D)-rC-P(D)，特別地，當P={a}時，屬性a關于D的重要性定義為σ(P)=rC(D)-rC-P(D).

3 粗糙集理論在數據分析中的應用

目前，基于粗糙集理論的方法逐漸成為數據分析主流方法之一.利用粗糙集理論進行數據分析一般可分為以下五個過程：

1.數據準備及預處理：在現實世界的很多情況下，我們拿到的第一手數據都會存在噪音數據、空缺數據和不一致性數據等我們不希望出現的數據，因此，首先要對數據進行必要的處理，包括數據刪除、數據補充、數據轉換等，從而為下一步數據分析提高良好的處理環境，并且還要明確條件屬性和決策屬性.

2.建立決策表：對于處理好的數據用一個信息系統S=(U,A,V,F)給表示出來.

3.屬性約簡及屬性重要度計算：屬性約簡就是在保持知識庫分類能力不變的條件下刪除其中不相關或不重要的冗余屬性，得到一個最簡潔的決策即最小（最優）約簡.在決策表中，不同屬性可能有不同的重要性，如果重要度為0則說明此屬性為冗余屬性，可刪除，通過計算每個屬性的重要程度則可以更加有效地進行屬性約簡.

4.規則提取：直觀地講就是將每個約簡用在決策表的每個對象上，從表中讀出適當的屬性值來形成決策規則.用類似邏輯語言中α→β的形式表示決策規則，α和β分別稱為決策規則的前件和后件，α代表條件屬性值的組合.

5.決策分析：根據生成的規則進行數據分析，得到有用的結論.

下面我們用一個具體實例進行闡述：通過利用粗糙集理論來分析影響學生《高等數學》課程學習成績的因素，以期量化學習成績和學習因素之間的關系，為教師能夠更好地進行教學和培養合格的人才提供一定的理論支持.

1.數據準備及預處理

首先采用問卷調查的方法，對安徽國際商務職業學院2015級會計專業56名學生進行了問卷調查（表1），采取隨機抽樣的原則抽取研究對象，共發放問卷56份，回收率100%，有效問卷56份，有效率100%.調查問卷分別從興趣、高考成績、課堂表現等六個方面提出問題，受調查者根據實際情況選出自己的答案選項，因此，各影響學習的因素屬性分別記為C1：興趣、C2：數學基礎（高考成績）、C3：課堂表現、C4：作業完成情況、C5：教師授課水平、C6：學習時間，選項ABCDE在決策表中分別用12345代替；決策屬性為期末考試成績，記作D，其中在[90,100]之間為優秀，[75,90)之間為良好，[60,75)之間為合格，[0,60)不合格，分別以1、2、3、4表示.將每一類中的所有實例的集合作為論域，每個實例作為論域中的對象，成績影響因素集作為條件屬性集，學生期末考試成績作為決策屬性.

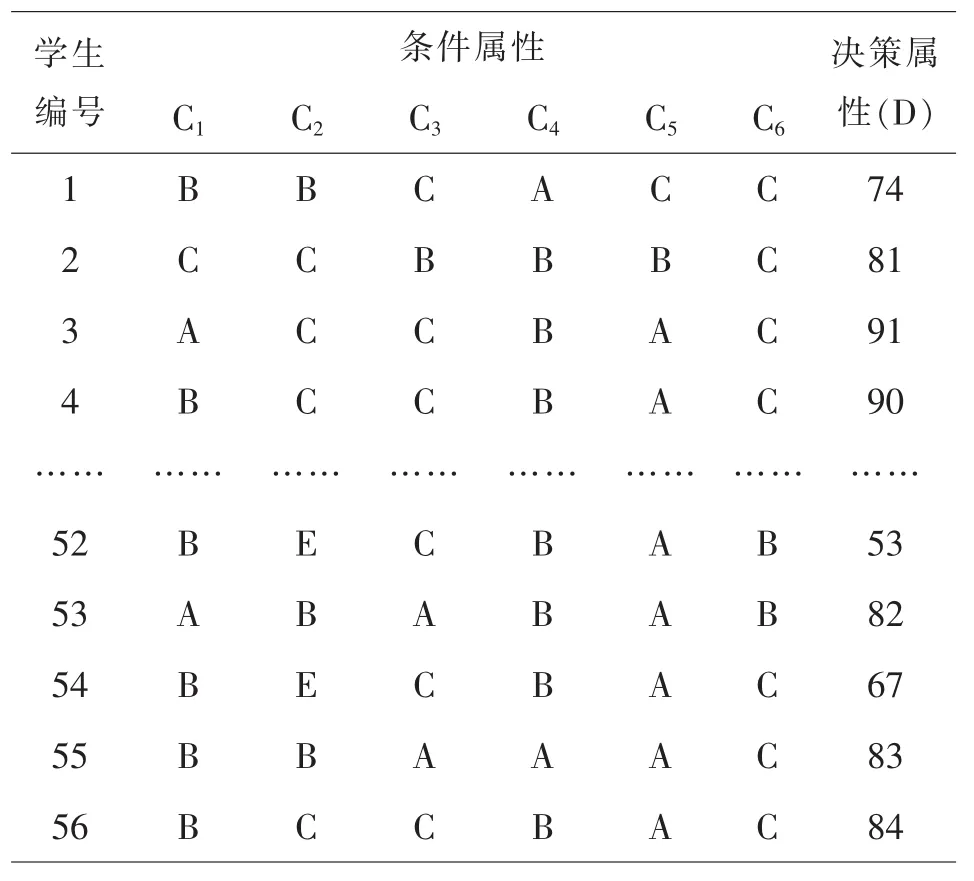
表1 調查問卷

2.根據以上數據可建立成績影響因素決策表（表2）.

3.利用屬性約簡算法進行屬性約簡，并計算屬性重要度.

（1）屬性約簡：利用屬性約簡算法進行約簡，可知C1—C6所有屬性均為不可約屬性.

（2）計算屬性重要度.首先計算出二維決策表中決策屬性D相對于條件屬性C的正域POSC(D)，根據粗糙集中的依賴度函數，計算出決策屬性D對條件屬性C的依賴程度.

表2 決策表

其次，計算二維決策表中每一個屬性Ci(i=1,2,…,6)對于決策屬性D的重要度σ(Ci)=rC(D)-rC-Ci(D)，其中rC-Ci(D)表示在條件屬性C中去掉Ci后，決策屬性D對條件屬性C的依賴程度，σ(Ci)的值越大，說明屬性Ci對分類的重要性越大，如果σ(Ci)=0，則說明屬性Ci對分類不起作用，可以忽視其影響.

利用數學軟件MATLB編程對二維決策表進行計算：得到各屬性相應的依賴度及重要性有：

由此可見，σ(C6)＞σ(C2)=σ(C3)＞σ(C5)＞σ(C4)＞σ(C1)

4.規則提取：根據約簡后的決策表提取規則，選取部分如下：

規則1：C1(1)∧C2(2)∧C3(1)∧C4(1)∧C5(1)∧C6(2)=＞D(1)

規則2：C1(2)∧C2(2)∧C3(4)∧C4(2)∧C5(2)∧C6(4)=＞D(4)

……

5.決策分析.

針對以上計算結果，我們進行進一步分析可知：

（1）興趣、基礎、課堂、作業、教師、學習時間等都是影響學生學習高等數學的重要因素；

（2）這六個影響因素的重要程度排序為：學習時間＞數學基礎（高考成績）=課堂表現＞教師授課水平＞作業完成情況＞興趣.因此，可以看出學生學習成績好壞很大程度上取決于自身的努力程度（即所花時間的多少），同時，學生在學習過程中要緊緊抓住課堂時間，邊聽邊記邊思考，只有這樣才能取得較好的學習效果；

（3）根據提取的規則可以得到相應的結論，比如從提取的規則1中可以看出當一個學生在這六個方面都做得很好時，一定可以取得優秀的成績，反之，由規則2得出雖然基礎較好，但是如果上課不聽課，課后自己不花時間努力學習，那么成績必然不及格；

（4）從數據中可以看出數學基礎也是影響大學生學好高等數學的一個非常重要的因素，這主要是由于數學課程具有連續性的特點，因此，對于一些基礎較差、尤其是沒有參加高考，自主招生進來的學生來講，學習高等數學的難度更大，故而，要求我們教師在針對這部分學生時，應該更加關注他們，在教授過程中更耐心一些，更詳細一些.

4 結束語

粗糙集理論作為一種新的處理含糊性和不確定性問題的數學工具，為數據分析提供了一條嶄新的途徑，其在數據挖掘中的應用研究目前正成為信息科學中的一個研究熱點，發展空間廣闊.

〔1〕張文修，吳偉志，梁吉業，李德玉.粗糙集理論與方法[M].北京：科學出版社，2001.1-25.

〔2〕安海忠，鄭鏈，王廣祥，等.粗糙集知識發現的研究現狀和展望.計算機測量與控制，2003（2）:81-83.

〔3〕史忠植.知識發現[M].北京：清華大學出版社, 2002.26-28.

TP274

：A

：1673-260X（2017）03-0022-03

2016-11-25