關于Wendt操作對鏈環交叉數的進一步結論

譚秋月， 孫平安， 林姝妤

(1. 武夷學院 數學與計算機學院， 福建 南平 354300；2. 武夷學院 實驗室管理中心， 福建 南平 354300；3. 廈門大學 數學科學學院， 福建 廈門 361000)

關于Wendt操作對鏈環交叉數的進一步結論

譚秋月1， 孫平安2， 林姝妤3

(1. 武夷學院 數學與計算機學院， 福建 南平 354300；2. 武夷學院 實驗室管理中心， 福建 南平 354300；3. 廈門大學 數學科學學院， 福建 廈門 361000)

研究紐結的一種解結操作——Wendt操作對鏈環交叉數的影響.計算紐結表中交叉指標不超過10的紐結，以及交叉指標不超過9的2分支鏈環的擬解結數，得到Wendt操作對這類鏈環的交叉數減二的結論.最后，通過投影圖給予證明. 關鍵詞： 紐結； 鏈環； Wendt操作； 解結數； 交叉指標

1 基本定義和引理

三維空間中，不與自己相交的連通分段線性閉曲線稱為紐結，而由有限條既不自交也不互交的連通的分段線性閉曲線構成的空間圖形稱為鏈環.只要投影方向選取適當，總可使鏈環的平面投影圖的自交點全部為二重點.為了反映產生二重點的弧線在三維空間的上下情況，用斷開的弧線表示下線，用連續的弧線表示上線.這樣二重點就變成了交叉點.以線的虛實表現交叉的情況，就得到鏈環的投影圖.一個鏈環投影圖稱為可分離的，若它是由多個無公共交叉點鏈環投影圖構成的，一個鏈環只有一個分離投影圖,則稱為不可分離或連通的.

設K為S3中的一個紐結，在K的所有投影圖中，交叉點最少的那個投影圖上的交叉點數就稱為K的交叉指標，其符號為c(K).

設L為一個有向鏈環，VL(t)為L的Jones多項式[2]，定義spanv(L)為VL(t)的最高方次與最低方次之差，即spanv(L)=max degVL(t).

在文獻[3]中，Kauffman定義了無向鏈環投影圖的Kauffman尖括號多項式，假設D為鏈環無向投影圖，設[D]=[D](A，B，d)為D的Kauffman方括號多項式，〈D〉=[D](A，A-1，-A2，-A-2)為Kauffman尖括號多項式，定義spank(D)為(D)的最高方次與最低方次之差，spank(D)=max deg〈D〉-min deg〈D〉.令L是一個有向鏈環，D為L的有向投影圖，擰數w(D)定義為D的全體交叉點的正負號總和，Kauffman證明了VL(t)=(-A3)-w(D)〈D〉|A=t-1/4[2-3]，所以有spanv(L)=(1/4)spank(D).

引理1[2-4]令D為一個有向鏈環的無向投影圖，則：1) 若L是連通交錯鏈環，c(L)=spanv(L)=(1/4)·spank(D)；2) 若L是有n(L)個不可分分支的可分鏈環，c(L)=spanv(L)-n(L)+1=(1/4)·spank(D)-n(L)+1.

引理2[2，5]令D為連通約化交錯鏈環的投影圖，則有：1) max deg〈D〉=V+2W-2，V是D的交叉點數，W是B區域數，〈D〉中A的最高方次那一項對應的系數為(-1)W-1；2) max deg〈D〉=-V-2B+2，V是D的交叉點數，B是A區域數，〈D〉中A的最低方次那一項對應的系數為(-1)B-1.

由于鏈環投影圖與符號平面圖存在著一一對應，Kauffman[6]為符號圖構建了Tutte多項式.設G為符號圖，令Q[G]=Q[G](A，B，d)為對應G的Tutte多項式，簡稱為Q-多項式.

定義2[6]Q-多項式是按照如下兩點循環規則來進行定義的.1) 若En是有n個頂點的無邊圖，則Q[En]=dn-1.2) (a) 如果e是橋，則Q[G]=(A+Bd)Q[G/e]，若s(e)=+；Q[G]=(B+Ad)Q[G/e]，若s(e)=-；(b) 如果e是環，則Q[G]=(B+Ad)Q[G-e]，若s(e)=+；Q[G]=(A+Bd)Q[G-e]，若s(e)=-；(c) 如果e既不是橋也不是環，則有Q[G]=BQ[G-e]+AQ[G/e]，若s(e)=+；而Q[G]=AQ[G-e]+BQ[G/e]，若s(e)=-.

引理3[6]設G是符號平面圖，D(G)對應G的鏈環投影圖，則Q[G]=[D(G)].

設G是符號平面圖，G的分支對偶圖G*是對圖G的每個連通分支先各自求對偶圖，由這些對偶圖的不交并得到的圖.注意到G中的邊與G*中的邊是一一對應的，對每個邊e∈E(G)，在G*對應著符號與之相反的e*∈E(G*).

引理4 設G是符號平面圖，G*為G對應的對偶圖，則存在Q[G]=Q[G*].

引理5 假設G=(V，E)是連通圖，G+是基礎圖G的正圖，則有Q[G+]=A-|E|+2|V|-2TG(-A-4，-A4).

2 解結數和Wendt操作說明

解結數的另一個等價定義，即任取紐結K的一個投影圖，先任意選定一個交叉點做Wendt操作；接著，做一系列初等變化得到個新紐結的投影圖；然后，在這個新的投影圖上選定第二個交叉點做Wendt操作；再做一系列初等變化又得到個新紐結的投影圖，依次進行下去，直至這個紐結變為平凡紐結.若存在紐結K的一個投影圖，按照這個做法，只需n次改變交叉點就可使紐結變為平凡紐結，并且沒有比n次更少的可能，那么,就稱紐結K的解結數為n.顯然,平凡紐結u(01)=0，其他紐結的解結數均大于等于1.

圖1 三葉結的Wendt操作Fig.1 Triple junction Wendt operation

三葉結交叉指標為3，但是只需做一次Wendt操作就可以變成平凡紐結，所以u(31)=1，三葉結解結數為1，如圖1所示.

定理1[9]任給一個紐結K的投影圖，設其交叉點數為n，則總可以經過不超過?n/2次Wendt操作,把它變成平凡紐結的投影圖.

推論1[9]設紐結K有一個交叉點數為n的投影圖,則u(K)≤?n/2.

一般來說，很難找到紐結的解結數.比如，紐結83在紐結表[10]的投影圖上看，解結數好像是2，但是紐結83還有很多其他的投影圖.同樣，為了證明一個復合結的解結數不可以為1，從問題提出到找到證明也經過了100多年的時間.紐結K的解結數u(K)的上界可以使用相對簡單的技巧計算出來，但是卻很難得到確切值.Scharlemann[1]在1985年證明了解結數為1的紐結都是素紐結.

下面的紐結解結數圖表由Kirby[2]提供，其中，紐結929的解結數由Kirby證實，紐結10139，10152的解結數是由Kawamura[9]得出的，紐結949的解結數是由Stoimenow[11]用計算機計算出來的，紐結10154，10161則是Stoimenow[12]通過使用Slice-Bennequin不等式[13]找到的，紐結1011，1047，1051，1054，1061，1076，1077，10100的解結數目前為止依然未知.

已知具有n個交叉指數的素紐結總個數以指數級的速度增長.所以,文中只研究交叉指數少于10的紐結的解結數.因為u(K)=u(K*)，所以不考慮手性因素.

3 結論及其證明

例1 鏈環820的Wendt操作，結果如表1所示.

表1 鏈環820每個交叉點經過一次Wendt操作的結果

投影圖K的擬解結數的定義可參考文獻[14-16].若經過Wendt操作得到的紐結為非交錯紐結，則存在減少1的情況，如交錯紐結933.

交叉點數少于10的交錯紐結投影中，對其一個交叉點做Wendt操作，若得到的紐結仍然為交錯紐結，則其交叉指標至少減少2；若不是，則不然.對交叉點數少于9的2個分支鏈環，此結論也成立，故這一規律在增加適當條件的基礎上得到定理2.

證明 令L為連通鏈環，其最約化交錯投影圖為D，因為L是連通的，則D一定是連通的.令G=G(D)為對應D的符號平圖.不失一般性，假設G是正圖，否則的話，可以根據引理1～4改為研究G*，因為是最約化的，所以G就是無環無橋.

情況Ⅰ 無環.

的確是胡鬧。西雙說，假如我們真的又產生感情，真的對那段婚姻戀戀不舍，婚后真的可以夫妻恩愛白頭偕老，復婚也未嘗不可。但是可以肯定的是，我與她，不可能再有絲毫感情——我指的是夫妻間的那種感情。我去看她，我借給她錢，都不過只是憐憫——我不忍心讓她死在那個出租屋里，就這樣。

在這個情況下,G′是連通無環無橋的正圖.因此,其對應的鏈環投影圖也是連通最約化的交錯投影圖.令H為連通平圖，v(H)，e(H)，f(H)分別定義為H的點數、邊數和面數.通過引理2可得到如下4點結果.

1) max degQ[G]=max deg〈D〉=V+2W-2=e(G)+2f(G)-2，對應的系數為(-1)f(G)-1；

2) min degQ[G]=min deg〈D〉=-V-2B+2=-e(G)-2v(G)+2，對應的系數為(-1)v(G)-1；

3) max degQ[G′]=e(G′)+2f(G′)-2=e(G)+2f(G)-3，對應系數為(-1)f(G′)-1=(-1)f(G)-1；

4) min degQ[G′]=-e(G′)-2v(G′)+2=-e(G)-2v(G)+5，則其對應的系數為(-1)v(G′)-1=(-1)v(G)-1.

由此,還可以得到如下4點結果.

1) max degA2Q[G]=e(G)+2f(G)，對應的系數為(-1)f(G)-1；

2) max degA2Q[G]=-e(G)-2v(G)+4，對應的系數為(-1)v(G)-1；

3) max deg (A-1-A3)Q[G′]=e(G)+2f(G)，對應的系數為(-1)f(G)-1；

4) max deg (A-1-A3)Q[G′]=-e(G)-2v(G)+4，對應的系數為(-1)v(G)-1.

A2Q[G]與(A-1-A3)Q[G′]的最大方次可互相削去，由此得到

所以有

spanq(G)=max degQ[G]-min degQ[G]= 2e(G)+2f(G)+2v(G)-4，

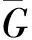
2e(G)+2f(G)+2v(G)-12=spanq(G)-8.

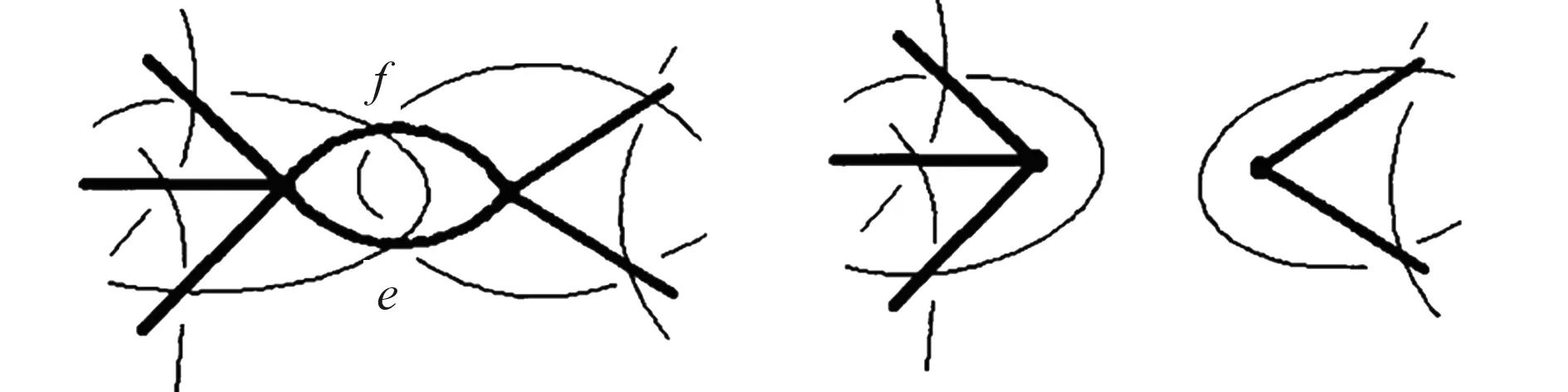
圖2 刪除平行邊e和f后的G圖形變為G-e-f圖形Fig.2 G into gigure G-e-f after delete parallel sides e and f

情況ⅡG′有環.令f為G′的任一個環.由于G是無環的，f一定是G的邊e的平行邊，再分兩種情況討論.

ⅱ) 如果G-e-f是連通的.首先知道f不是G′的橋.令g≠f為G′的邊，因為G是無橋的，g屬于G中一個圈C，若e?E(C)，g屬于G′中一個圈C中；若e∈E(C)，g屬于G′中的一個圈G′=C-e+f，所以g不是橋.因此,G′為連通無環無橋的正圖，同樣由引理2可得到到如下4點結果.

1) max degQ[G]=max deg〈D〉=V+2W-2=e(G)+2f(G)-2，對應的系數為(-1)f(G)-1；

2) min degQ[G]=min deg〈D〉=-V-2B+2=-e(G)-2v(G)+2，對應的系數為(-1)v(G)-1；

3) max degQ[G′]=e(G′)+2f(G′)-2=e(G)+2f(G)-5，對應系數為(-1)f(G′)-1=(-1)f(G)-1；

4) min degQ[G′]=-e(G′)-2v(G′)+2=-e(G)-2v(G)+3，則其對應的系數為(-1)v(G′)-1=(-1)v(G)-1.

因此，可以得到如下4點結果.

1) max degA-2Q[G]=e(G)+2f(G)-4，對應的系數為(-1)f(G)-1；

2) max degA-2Q[G]=-e(G)-2v(G)，對應的系數為(-1)v(G)-1；

3) max deg (A-1-A-3)Q[G′]=e(G)+2f(G)-4，對應的系數為(-1)f(G)-1；

4) min deg (A-1-A-3)Q[G′]=-e(G)-2v(G)，對應的系數為(-1)v(G)-1.

A-2Q[G]與(A1-A-3)Q[G′]的最大方次可互相削去，由此可得

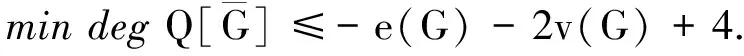
所以有

2e(G)+2f(G)+2v(G)-12=spanq(G)-8.

[1]SCHARLEMANNMG.Unknottingnumberoneknotsareprime[J].InventMath，1985,82(1):37-55.

[2]KAUFFMANLH.StatemodelsandtheJonespolynomial[J].Topology，1987,26(3):395-407.

[3]MURASUGIK.Jonespolynomialsandclassicalconjecturesinknottheory[J].Topology，1987，26(2):187-194.

[4]THISTILETHWAITEMB.AspanningtreeexpansionoftheJonespolynomial[J].Topology，1987，26(3):297-309.

[5]KAUFFMANLH.Newinvariantsinthetheoryofknots[J].AmerMathMonthly，1988(95):195-242.

[6]KAUFFMANLH.ATuttepolynomialforsignedgraphs[J].DiscreteApplMath，1989,25(1/2):105-127.

[7]BONDYJA，MURTYUSR.Graphtheoryanditsapplications[M].London:TheMacmillanPressLtd，1976:1-40.

[8]KIRBYR.Problemsinlow-dimensionaltopology[C]∥GeorgiaTopologyConference.Providence:[s.n.],1996:35-473.

[9]KAWAMURAT.Theunknottingnumberof10139and10152are4[J].OsakaJMath，1998,35(3):539-546.

[10] ADAMS C C.The knot book[M].New York:American Mathematical Society Providence Ri,1994:307.

[11] STOIMENOW A.Polynomial values， the linking form， and unknotting numbers[J].Math Res Lett,2004,11(5/6)：755-769.

[12] STOIMENOW A.Positive knots, closed braids and the Jones polynomial[J].Annali Della Scuola Normale Superiore Di Pisa Classe Dienze,1998,2(2):237-285.

[13] JONES V F R.A polynomial invariant for knots via von Neumann algebras[J].Bull Amer Math Soc,1985,12(1):103-111.

[14] 譚秋月,孫平安,林姝妤.Wendt操作對紐結和鏈環影響的若干規律[J].石家莊學院學報,2015,17(6):61-66.

[15] 李景文，呂楠，陸妍玲，等.對象化BR-TIN模型三維地理信息組織方法[J].華僑大學學報(自然科學版)，2015，36(4):383-387.

[16] 汪秋分,宋海洲.圖的拉普拉斯譜半徑對應的特征向量性質及其應用[J].華僑大學學報(自然科學版),2014,35(1):107-111.

(責任編輯： 黃曉楠 英文審校： 黃心中)

Further Conclusion of Crossing Number of Links Based on Wendt Operation

TAN Qiuyue1， SUN Ping′an2， LIN Shuyu3

(1. School of Mathematics Science and Computer， Wuyi University， Nanping 354300， China；2. Laboratory Management Center， Wuyi University， Nanping 354300， China；3. School of Mathematical Sciences， Xiamen University， Xiamen 361000， China)

The effect of a single splitting operation, Wendt operation on the crossing number of the link diagrams is researched. We calculate the Quasi-splitting number of these two numbers for knots, which are with crossing number no more than 10, and with crossing number no more than 9 and 2-comonent links in the Knot table. One conclusion is that the Wendt operation can make the crossing number of these link diagrams minus two. In the last, we give a strict graph-theoretical proof by the projection drawings. Keywords： knot； link； Wendt operation； unknotting number； crossing number

10.11830/ISSN.1000-5013.201702027

2017-02-14

譚秋月(1980-)，女，副教授，主要從事圖論、離散數學的研究.E-mail:tqyspa@163.com.

福建省教育廳科技項目(JA1551)； 福建省大學生創新創業訓練計劃項目(201510397029)； 武夷學院科研基金資助項目(XL201409)

O 157.5

A

1000-5013(2017)02-0276-05