基于人工蜂群算法優(yōu)化BP神經網絡的交通流預測

李文越，周思源，龐京城

(1.長安大學公路學院，陜西西安 710064；2.江蘇交科交通設計研究院有限公司，江蘇淮安 223001)

基于人工蜂群算法優(yōu)化BP神經網絡的交通流預測

李文越1，周思源1，龐京城2

(1.長安大學公路學院，陜西西安 710064；2.江蘇交科交通設計研究院有限公司，江蘇淮安 223001)

建立基于人工蜂群算法(Artificial Bee Colony Algorithm，ABC)優(yōu)化BP(Back Propagation)神經網絡(ABC-BP)的分析預測模型，對城市道路短時交通流進行預測。以BP神經網絡為基礎，通過人工蜂群算法優(yōu)化神經網絡的各個權值和閾值，考慮交通流的時間特性，將歷史交通流量作為訓練樣本，預測某日的交通流量。多種算法的仿真試驗對比表明：基于ABC-BP的預測結果比傳統(tǒng)BP神經網絡、小波預測神經網絡以及PSO(Partide Swarm Optimization)-BP神經網絡的預測結果更加精確。

人工蜂群算法；BP神經網絡；交通流預測；仿真

隨著家庭汽車數量的增多，居民出行需求日益增長，城市道路更加擁堵，因此使用智能交通系統(tǒng)(intelligent transportation system，ITS)誘導和控制道路上的交通流，利用現有交通資源更好的緩解城市交通壓力，已經成為解決城市交通問題的重要手段。研究智能交通最關鍵的內容之一是實時交通分配(Real-Time-Dynamic Traffic Assignment)系統(tǒng)，其內容主要包含：預測城市的道路交通網系統(tǒng)狀況；提供道路交通流的引導方向，指引車流使之分配于最合適的道路網；給出行者提供合適的出發(fā)時間、交通方式和出行路徑的選擇建議。交通誘導系統(tǒng)需要根據t時刻的歷史交通量，判斷預測t+1時刻以及更遠期的交通量。預測短時交通量的難點在于交通流的不確定性和不規(guī)律性。

目前已經有多種短時交通流預測方法，包括卡爾曼濾波預測模型[1]、時間序列預測模型[2]、非參數回歸預測模型[3-4]、混沌理論預測模型[5-6]、支持向量機預測模型[7-8]、K近鄰預測模型[9]等。近年來，隨著機器學習、智能算法、云計算的不斷發(fā)展和深入，反向傳播神經網絡模型[10]、徑向基函數RBF(Radial Basis Function)神經網絡模型[11-13]、小波神經網絡模型[14-15]等各類神經網絡模型被廣泛用于確定路段上的交通流量。

BP神經網絡在反應交通流的復雜性、突變性等方面不具有較好的魯棒性，當發(fā)生突發(fā)事件或者某些特殊情況時，交通流將會發(fā)生變化，使預測結果出現大的偏差。本文將BP神經網絡以及人工蜂群算法進行融合，充分發(fā)揮人工蜂群算法結構簡單、全局尋優(yōu)性能好的特性，優(yōu)化BP神經網絡權值和閾值，遞減網絡的訓練時間，以提高對交通流預測的精準性和魯棒性。

1 ABC算法的基本原理

ABC算法是由Karaboga在2005年根據蜂蜜的群體配合尋找食物的行為提出的，在組合優(yōu)化和求解中具有良好的效果[16]。

該算法中，蜜蜂被劃分為引領蜂、跟隨蜂及偵查蜂3種類型。其中花蜜源由偵查蜂來尋找，另外兩種蜂負責開采蜂蜜[17-18]。引領蜂搜索蜜源并根據蜜源大小和數量進行標記，同時散發(fā)與之相當數量的標記蜜源路徑信息，并呼喚更多的蜜蜂前來開采。跟隨蜂采用隨機的方式去抉擇標記的蜜源，與此同時也在搜索附近新的蜂蜜源，以尋找效益較高的蜜源開采。如果在采蜜過程中的某一段時間，蜜蜂對其中一個蜜源進行開采，還會派遣新的偵查蜂去尋找新的蜂蜜源來取代當前的蜂蜜源，以使蜂蜜變得最豐富。

ABC算法的優(yōu)點：該算法在整個全局中收斂，且收斂迅速[19]；該算法的適應范圍非常寬泛，能優(yōu)化各個領域中的各種問題；算法設置參數相對較少；ABC是一種基于種群并行優(yōu)化的算法，容易實現和處理[20]。

2 BP神經網絡算法

2.1 基本原理

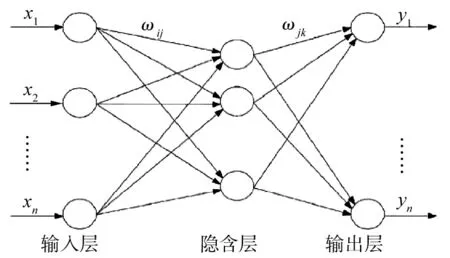
圖1 BP神經網路結構模型

BP神經網絡是多層前饋式誤差反傳神經網絡。其網絡結構模型由輸入層、輸出層和若干隱含層3部分連接而成，其中每一層都由無數個節(jié)點交錯映射連接而成。一個神經元由一個節(jié)點表示，上層節(jié)點與下層節(jié)點之間通過權連接，層與層之間的節(jié)點采用全互聯的連接方式，每層內節(jié)點之間沒有聯系。在一個3層前饋網絡中，只要隱節(jié)點足夠多，就可以解決任意的工程問題。因此，BP 算法的3層MLP(Multi-Layer feedforward Perceptron)結構包含有1個輸入層、1個輸出層及1個隱含層，如圖1所示。圖1中：x1，x2，……，xn為輸入層，y1，y2，……，yn為輸出層，wij、wjk分別為連接輸入層、輸出層與隱含層之間的權重。

2.2 預測步驟

1)確定輸出變量。根據實際情況，確定輸出變量的屬性和個數。在交通流預測中，輸出變量為該預測路段一定時間內的交通量。

2)選擇輸入變量。本文通過前幾日交通流量的歷史數據對該時間的交通流量進行預測。因此選擇前幾日的交通流量數據作為輸入變量。

3)數據預處理。對所輸入的數據進行分類處理，確定訓練樣本和驗證樣本集合。確定BP 網絡結構與訓練方法。

4)建立BP模型進行預測。用訓練樣本集合對BP 模型中的參數進行標定，這些參數包含隱含層節(jié)點的數量和權值。最后與實際數值進行對比分析。

3 基于ABC-BP的交通流預測

基于ABC-BP的交通流預測模型如圖2所示。

1)生成一個BP神經網絡并初始化此BP神經網絡。

2)初始化人工蜂群算法的相關參數，主要參數包含人工蜂群數量Nc、引領蜂數量Ne、跟隨蜂數量No、蜂群算法解的個數Ns、最優(yōu)解更新失敗次數的閾值、最大循環(huán)次數M等。其中，Nc=Ns=Ne+No。初始種群及初始解Xi(i=1,2，……，Ns)在(-1,1)隨機產生一個數值，Xi表示步驟1)中創(chuàng)建的BP神經網絡的鏈接權值和閾值，維數D滿足

D=NinNh+Nj+NhNout+Nout，

式中：Nh為BP基函數；Nin和Nout分別為神經網絡中輸入層和輸出層神經元的個數。

3)計算每個解的適應度函數 ，有

式中TMSEi為第i個解的神經網絡均方誤差。

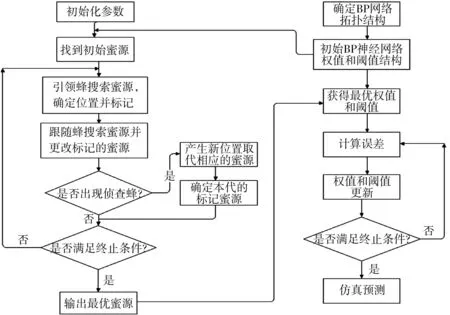
圖2 ABC-BP神經網絡模型

4)計算蜜蜂解的最佳收益率

根據各項收益率，從當前解的領域中挑選出新的最優(yōu)解。

5)若最優(yōu)解更新失敗的總數大于設定的閾值，意味著這個解陷入了局部最優(yōu)，而并非全局最優(yōu)解，因此偵查蜂丟棄此解尋求新解Xi′，有

Xi′=Xmin+rand(0,1)(Xmax-Xmin)

，

(1)

式中：Xmin為局部解的最小值；Xmax為局部解的最大值；rand(0，1)為歸一化函數，即把Xmax與Xmin的差值歸一化到0到1之間。

由式(1)解出新的解將原來的解代替，如此反復，最后得出蜜源豐富的最優(yōu)解。

6)若人工蜂群算法的迭代次數超過預先設定的閾值，說明這個解不能被繼續(xù)優(yōu)化，偵查蜂會將它舍棄，通過式(1)產生的新解將其替換，保存最優(yōu)的解。

7)若蜂群算法迭代次數超過預先設置的最大循環(huán)次數M，則結束BP神經網絡的訓練。否則返回步驟4)。

8)BP神經網絡的連接權值和閾值用得到的最優(yōu)解變換而來，繼續(xù)用數據仿真和測試神經網絡，達到預測路段交通流量的目的。

4 實例分析

4.1 數據樣本的選擇

選取西安三環(huán)某路段作為研究對象，運用ABC-BP模型對路段某個時刻的流量進行預測分析。

城市交通流在時間特征上有一定的周期性，某種程度上，居民出行的規(guī)律揭示了交通流的變化。城市道路交通量在日常工作日內變化不大，周末及重大節(jié)日流量有所變化。每小時交通量的變化情況(時變化)反映了連續(xù)24 h內交通流的變化情況，通常，日常工作日內的時變化呈馬鞍型，有早高峰、平峰以及晚高峰的出現。交通流時間序列具有長程相關性，即現在和未來交通狀態(tài)受歷史交通狀態(tài)的影響，并且交通流時間變化的趨勢和歷史時間序列變化的趨勢呈正相關[20]。

選取該路段7個工作日2015-05-09、2015-05-12—16、2015-05-19的試驗測得的全日交通流量數據作為樣本數據，路段周邊地區(qū)無較大活動并且天氣晴朗。24 h內每隔20 min記錄1次數據，共記錄504組數據。把前6 d的432組數據作為訓練樣本，用于ABC-BP神經網絡模型的訓練，用訓練好的預測模型對后面1 d的72組數據進行預測。

4.2 仿真試驗環(huán)境

仿真采用Pentium 2.0 GHz處理器、2 GB內存PC機，算法由MATLAB實現。設置運行環(huán)境的初始規(guī)模為50個跟隨蜂和50個引領蜂，100次嘗試次數以及迭代次數。設定BP神經網絡的閾值平均相對誤差≤3%時進化結束；當該神經網絡達到最大訓練次數時進化也結束。BP神經網絡的最優(yōu)權值和閾值先使用人工蜂群算法進行優(yōu)化，再使用優(yōu)化后的BP神經網絡算法對道路流量進行預測。

4.3 建立仿真試驗模型

本次試驗中，訓練神經網絡的輸入層為當前時間點前的432個交通流量的數據，隱含層中的節(jié)點數L應同時滿足

式中：m為輸出層節(jié)點數；k為輸入層節(jié)點數；α=1～10。

設k=25，m=1，經計算得L=4，學習效率取0.1，訓練次數取1 000，輸出目標值取0.000 4。

4.4 仿真試驗結果比較

將ABC-BP神經網絡、PSO-BP神經網絡、傳統(tǒng)BP神經網絡、小波神經網絡4種算法的預測值進行直觀對比，如圖3～6所示。圖3～6中橫坐標每小格表示以每20 min為單位的時間序列。

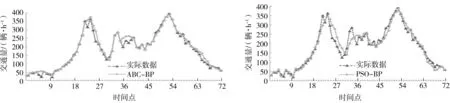
圖3 ABC-BP神經網絡預測 圖4 基于PSO-BP神經網絡預測

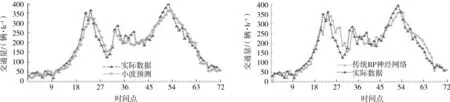
圖5 傳統(tǒng)BP神經網絡的預測 圖6 小波神經網絡的預測

從圖3～6中可以看出，圖3的預測值和實際數據最接近，表明ABC-BP神經網絡預測模型相對于另外3種預測模型能更準確的預測短時路段的交通流量。

為了更好說明上述4種算法的濾波處理效果，采用3種誤差表示方式對比幾種算法的誤差，有

表1 幾種模型的3種誤差比較

式中：P(t)為預測交通量；R(t)為實際交通量；S為整個時段中預測交通量的樣本總數；TMAE為平均絕對值誤差；TREmax為絕對值最大誤差；TRMSE為均方根誤差。

幾種算法的誤差值對比如表1所示。

從表1可以看出， ABC-BP算法的3種誤差均比其他3種算法的誤差小，預測結果最準確，其交通流量預測值最接近路段流量的真實值。

5 結論

1)建立基于蜂群算法的BP神經網絡預測模型，并將其用于短時交通流預測，預測精度高于PSO-BP神經網絡、傳統(tǒng)BP神經網絡、小波神經網絡等算法，可以為交通流的誘導和控制提供更加精確的預測效果。

2)該算法未考慮到交通流預測中的其他外部因素，僅使用歷史交通流量數據作為訓練對象，有待采用更好的智能算法進行優(yōu)化處理。

[1]OKUTANI I, STEPHANEDES Y J.Dynamic prediction oftraffic volume through Kalman filtering theory[J].Transportation Research Part B：Methodological, 1984，18(1)：1-11.

[2]姚志勝，邵春福.基于于狀態(tài)空間模型的道路交通狀態(tài)多點時間序列預測[J].中國公路學報，2007，20(4)：113-117. YAO Zhisheng, SHAO Chunfu.Road traffic state multi spot time series forecasting based on state space model[J].China Journal of Highway and Transport，2007，20(4)：113-117.

[3]劉洋，馬峰.基于聚類分析的非參數回歸短時交通流預測方法[J].交通信息與安全，2013，31(2)：27-32. LIU Yang，MA Feng.Non-parametric regression for short-term traffic flow forecasting based on cluster analysis[J].Journal of Transport Information and Safety，2013，31(2)：27-32.

[4]宮曉燕，湯淑明.基于非參數回歸的短時交通流量預測與事件檢測綜合算法[J].中國公路學報，2003，16(1)：52-56. GONG Xiaoyan, TANG Shuming.Integrated traffic flow forecasting and traffic incident detection algorithm based on non-parametric regression[J].China Journal of Highway and Transport,2003,16(1):52-56.

[5]賈顯超，陳旭梅，弓晉麗.基于混沌理論的短期交通流量多步預測[J].交通信息與安全，2013，31(6)：27-35． JIA Xianchao, CHEN Xumei, GONG Jinli.Multi-step short-term traffic flow prediction based on chaotic theory[J].Journal of Transport Information and Safety,2013,31(6):27-35.

[6]李松，劉力軍，解永樂.遺傳算法優(yōu)化BP神經網絡的短時交通流混沌預測[J].控制與決策，2011，26(10)： 1581-1585. LI Song, LIU Lijun, XIE Yongle.Chaotic prediction for short-term traffic flow of optimized BP neural network based on genetic algorithm[J].Control and Decision，2011，26(10)：1581-1585.

[7]HONG W C，DONG Y C，ZHENG F F，et al.Forecasting urban traffic flow by SVR with continuous ACO[J].Applied Mathematical Modeling，2011，35(3)：1282-1291.

[8]傅貴，韓國強，逯峰，等.基于支持向量機回歸的短時交通流預測模型[J].華南理工大學學報(自然科學版)，2013，41(9)：71-76. FU Gui, HAN Guoqiang， LU Feng, et al.Short-term traffic flow forecasting model based on support vector machine regression[J].Journal of South China University of Technology(Natural Science Edition)，2013，41(9)：71-76.

[9]WU C H，WEI C，CHANG M.Travel time prediction with support vector regression[J].IEEE Transactions on Intelligent Transportation Systems，2004，5(12)：276-281．

[10]HUANG K, CHEN S, ZHOU Z G.Research on non-linear chaotic prediction mode for urban traffic flow[J].Journal of Southeast University:English Edition，2003，19(4)：411-413．

[11]VYTHOULKAS PC.Alternative approaches to short term traffic forecasting for use in driver information systems[M].Berkeley: Elsevier Science Publishers，1993．

[12]LEDOUX Corinne.An urban traffic flow model integrating neural network[J].Transportation Research Part C:Emerging Technologies，1997，5(5)：287-300．

[13]張濤，陳先，謝美萍，等.基于K近鄰非參數回歸的短時交通流預測方法[J].系統(tǒng)工程理論與實踐，2012，30(2)：376-384. ZHANG Tao, CHEN Xian, XIE Meiping，et al.K-NN based nonparametric regression method for short-term traffic flow forecasting[J].Systems Engineering-Theory & Practice，2012，30(2)：376-384.

[14]李松，劉力軍，翟曼.改進粒子群算法優(yōu)化BP神經網絡的短時交通流預測[J].系統(tǒng)工程理論與實踐，2012，32(9)：2045-2049. LI Song，LIU Lijun，ZHAI Man.Prediction for short-trem flow traffic based on modified PSO optimized BP neural network[J].Systems Engineering-Theory & Practice，2012，32(9)：2045-2049.

[15]高為，陸百川，贠天鸝，等.基于時空特性和RBF神經網絡的短時交通流預測[J].交通信息與安全，2011，29(1)：16-19. GAO Wei，LU Baichuan，YUN Tianli,et al.Short-term traffic flow forecasting based on spatiotemporal characteristics of traffic flow and RBF neural network[J].Journal of Transport Information and Safety，2011，29(1)：16-19.

[16]賀國光，馬壽峰，李宇.基于小波分解與重構的交通流短時預測法[J].系統(tǒng)工程理論與實踐，2002，9(2)： 101-107. HE Guoguang，MA Shoufeng，LI Yu.Study on the short-term forecasting for traffic flow based on wavelet analysis[J].Systems Engineering-Theory & Practice,2002,9(2):101-107.

[17]MUKHERJEE P，SATISH L.Construction of equivalent circuit of a single and isolated transformer winding form FRA data using the ABC algorithm[J].Power Delivery，IEEE Transactions on Automatic Control，2012，27(2)：963-970.

[18]ZHU G，KWONG S.Gbest-guided artificial bee colony algorithm for numerical function optimization[J].Applied Mathematics and Computation，2010，217：3166-3173.

[19]KANG F，LI J，MA Z.Rosenbrock artificial bee colony algorithm for accurate global optimization of numerical functions[J].Information Science，2011，181(16)：3508-3531.

[20]袁健，范炳全.城市道路短期交通流預測VHSSA模型[J].公路交通科技，2014，31(5)：135-136. YUAN Jian, FAN Bingquan.VHSSA model for predicting short-term traffic flow of urban road[J].Journal of Highway and Transportation Research and Development，2014，31(5)：135-136.

(責任編輯：楊秀紅)

Traffic Flow Prediction of BP Neural Network Optimized by Artificial Bee Colony Algorithm

LIWenyue1,ZHOUSiyuan1,PANGJingcheng2

(1.InstituteofHighway,Chang′anUniversity,Xi′an710064 ,China;2.TrafficDesignInstituteCo.,Ltd.ofJiangsuTransportationScience,Huaian223001,China)

The analysis and prediction model of the urban road short-term traffic flow is established based on a neural network optimized by the Artificial Bee Colony Algorithm. The thresholds and weights of the neural network are optimized by the Artificial Bee Colony Algorithm. Taking the time characteristic of the traffic flow into account, the historical traffic flow is used as the training sample to predict the traffic flow of a day. The contrast of stimulation tests of multi-algorithms shows that the prediction results based on ABC-BP are more accurate than those based on the traditional BP neural network, the wavelet neural network and PSO-BP neural network.

Artificial Bee Colony Algorithm; BackPropagation neural network; traffic flow prediction; simulation

2016-09-26

李文越(1993—)，男，江蘇揚州人，碩士研究生，主要研究方向為交通運輸規(guī)劃與管理、智能交通，E-mail：360585027@qq.com.

10.3969/j.issn.1672-0032.2017.01.006

U491.111.2

A

1672-0032(2017)01-0034-06