保拓撲結構的三維細化算法及三維非接觸測量

洪漢玉+馬爾威+黃麗坤

【摘要】 針對現有的三維細化算法會出現斷裂、不連續以及破壞物體原有的拓撲結構等問題，提出了一種基于保拓撲結構和具有旋轉不變性的新的三維細化算法。實驗結果表明，新的細化算法具有連通性保持不變，幾何及拓撲性質保持不變，及旋轉后細化結果保持不變的性質。

【關鍵詞】 三維細化 刪除模板 拓撲結構 旋轉不變性 三維非接觸測量

一、引言

圖像細化廣泛應用在各個領域，如醫學圖像分析，模式識別等。三維圖像細化是圖像處理和視覺分析的主要研究方向，細化提取的骨架是后續圖像分析和特征提取的重要基礎。從三維細化的結果中可提取基本尺寸和基準線、基準面等特征，包括物體的軸線基準、軸線長度，形狀結構及聯接關系。通過這一系列參數和特征準確表述和確定目標的當前狀態，從而實現對三維目標的全方位的非接觸測量。

三維細化算法主要包括提取中心線和提取中心面兩類，本文重點研究中心線的提取。在一個三維二值圖像中黑點和白點分別代表目標點和背景點，細化就是將逐層將黑點移除（黑點改為白點）直到僅剩一個像素寬的骨架。連通性及拓撲結構的保持是三維細化過程中考慮的主要問題，概括為三個方面：（1）輸入圖像中的任何物體不能被拆分或完全消除；（2）任何空腔不能與背景或另一個空腔合并；（3）不能消除或新增任何的空腔和孔洞。連通性的保持是拓撲性質的保持的基礎，例如形如“o” 的物體細化后不能形如 “c”，細化后提取的骨架應位于物體的中軸，并且看起來相似于原物體；同時細化算法在物體平移、比例變化及旋轉前后提取的骨架應基本保持一致。

提取中心線的三維細化算法多是基于模板的并行細化算法。并行細化算法有子迭代并行細化算法，區域并行細化算法[10，11]和完全并行細化算法三類。完整的基于模板的完全并行三維細化算法由Ma和Sonka提出，這一算法不能很好的保護三維物體的拓撲結構，后續研究者發現這一問題，Wang和Basu通過擴充刪除模板解決了某些情況下細化結果出現斷裂的情況，但仍存在一些問題，且由于刪除模板擴充后有方向性，不能保證三維物體旋轉后的細化結果保持不變。

針對上述問題，提出一種新的細化算法，從基礎模板在各個方向上旋轉得到具有各向同性的刪除模板，保證了模板的對稱性，使物體旋轉之后細化結果和旋轉前細化結果保持一致；給出了真偽刪除點的定義，并證明了提出的算法滿足連續性保持的條件，解決了點同時刪除造成不連續的問題。

二、三維細化旋轉不變性理論分析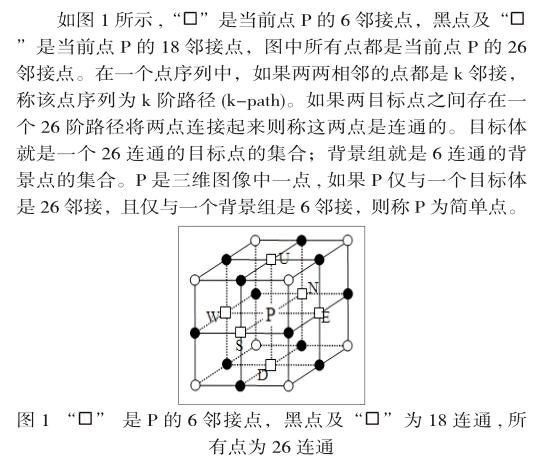

Wang和Basu針對Ma和Sonka的算法中不能保持連通性的情況對D類模板添加更多更細致的限制，擴充了最終的刪除模板。Ma算法中D類刪除模板是12個，Wang對模板中的一些點增加了限制，把D類模板擴充為36個。Ma算法中d7如圖2所示，Wang擴充后的d7如圖3所示。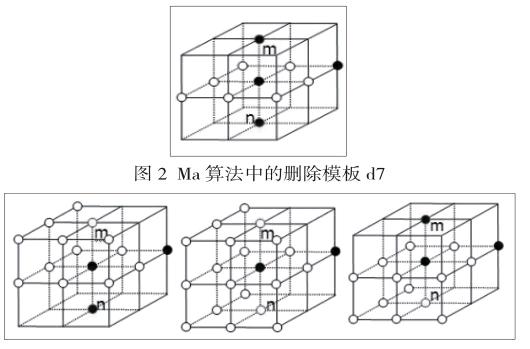

圖3 Wang算法中刪除模板d7-1，d7-2，d7-3算法主要步驟：

1）檢測邊界點（26鄰域內至少有一個是背景點）。

2）并行刪除滿足任一刪除模板的非尾點。

3）返回1）直到無任何點可以被刪除。

完全并行細化算法，從各個方向同時逐層刪除三維物體中的點，這保證了最終結果位于原物體的中軸上，且相似于原物體。但并行細化算法的細化結果有出現斷裂的可能，每一層的點在進行刪除模板的匹配及其他刪除條件的判斷時，若點與點之間相互為滿足刪除條件的必要點，同時刪除所有滿足條件的點得到的細化結果就可能出現斷裂，不能保持原物體的拓撲結構。

其他情況下仍仍然會出現斷裂，使最終細化結果無法保持原物體拓撲結構。同時因為只改變了某些方向上的模板，最終的刪除模板不再是完全對稱，使得細化算法不具旋轉不變性。

三、基于保拓撲結構和旋轉不變性的細化算法

針對上述分析提出一種新的基于保拓撲結構和旋轉不變的三維細化算法。首先給出旋轉不變性的定義，其次設計了各向同性的刪除模板，最后根據需要定義了真偽刪除點，并論述了提出的算法滿足連續性保持的條件。通過假設驗證法，檢測候選刪除點刪除前后26鄰域內目標體和背景組的數目變化，確認刪除點的真偽，保持了原有的拓撲結構，進而確保物體旋轉后細化結果的連續性不變。

關于旋轉不變性做如下定義：

定義1（旋轉不變性）：當物體相對之前位置旋轉后，通過細化提取的骨架與旋轉前提取的骨架形態及結構保持一致，簡稱該細化算法具有旋轉不變性。

為使旋轉后結果與旋轉前結果保持一致，本文構造了具有各向同性的刪除模板。如圖4所示，新算法中具有各向同性的D類刪除模板是12個，且模板中限制點比Ma算法中少。改進刪除模板是基于圖2中四類基本模板，通過繞三個中軸旋轉獲得，在結構上是完全對稱的，從而保證在各個方向模板是同性的，使新算法具有旋轉不變性。

為準確表達該算法，做如下定義：

定義2（真偽刪 除點）：在每次迭代中，通過與刪除模板的匹配，簡單點、非尾點的判斷選出候選點，假設所有候選點被刪除，再逐個檢驗候選點被同時刪除后26鄰域內目標體的數目和背景組的數目有沒有改變，若改變稱為偽刪除點，若未發生變化稱為真刪除點。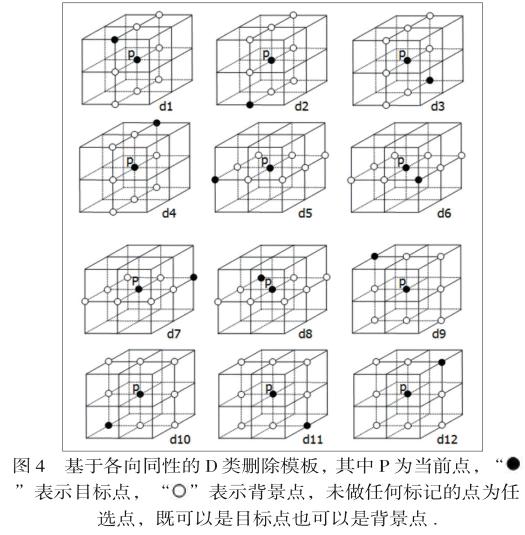

每次迭代中對符合刪除模板且滿足其他刪除條件的目標點做標記，假設標記點已全部被刪除（值為0），逐個對標記點位置進行檢測，檢測標記點位置26鄰域中目標點（黑點）的連通性，和18鄰域中背景點的連通性，若連通性發生改變則把標記點重置為1，若未改變確定刪除。因為在一次迭代中任何點的刪除不應該改變其26鄰域中目標點的連通性和18鄰域中背景點的連通性。這就有效防止同時刪除一系列點造成細化結果出現斷裂破壞拓撲結構的可能。

連通性證明：本文算法按照簡單點的定義選候刪除點，為保證被刪除的點是簡單點，在刪除前做如下判斷：判斷當前點26鄰域內的目標點是否連通；判斷當前點18鄰域內的背景點是否連通且至少有一個點與當前點是6鄰接，所以被刪除的點都是簡單點，滿足條件①。通過刪除點的真偽驗證表明對每一個刪除點來說，在其他點被刪除后，26鄰域內仍然只有一個目標體，18鄰域內只有一個背景組，即還是簡單點，所以每次迭代中同時刪除的所有點的集合是一個簡單點集合。那么屬于一個單位正方形上的兩個，三個或四個不同點被同時刪除時，它們也是簡單點集合，表明本文算法滿足條件②、③、④。假設存在一個包含在單位立方體內的目標體被完全刪除，那么單位立方體內八個點只能是可被刪除的點或者背景點，可被刪除的點必須滿足某一刪除模板，根據根據本文算法設計的刪除模板特點，八個點中總有一個面上的四個點必須同時是背景點，因此包含在一個單位立方體內能被完全刪除的目標體不存在，即滿足條件⑤。因此本文算法滿足三維細化算法保持連通性的條件。

基于保拓撲結構具有旋轉不變性的三維細化算法主要步驟：

1）檢測邊界點（26鄰域內至少有一個是背景點）；

2）檢測滿足任一刪除模板同時屬于非尾點和簡單點的點，并標記為候刪除點；

3）根據定義2判斷2）中標記的候刪除點的真偽，若為真，則確認刪除，否則不刪除；

4）返回1）直到無任何點可以被刪除。

四、 物體的尺寸提取與非接觸測量

對細化后的骨架進行像素數的統計可以得到三維模型的幾何尺寸信息，這些測量信息可以精準地描述三維模型的當前狀態。比如表面即為邊界點的集合，通過判斷是否具備空間26連通可以快速提取邊界點，表面積可以表示為邊界點像素的總和，這種表示方法不僅簡單，而且被證明是物體表面積的無偏和一致的最好估計。

根據三維圖像數據和尺寸基準線，可提出和計算目標的厚度、高度、徑向、軸向、位置等幾何尺寸，計算各組成部分的長度、高度、寬度或直徑、半徑等形狀參數，計算表面各部分的幾何距離，有關結構與重要基準面、基準線的距離以及平行度、平面度、圓度、同軸度等形位誤差。用這一系列參數和特征準確表達和確定目標的實際當前狀態，從而實現對目標的全方位的非接觸測量。

五、實驗結果與分析

該部分設置了四個實驗。在前兩個實驗中把新算法分別和Ma的算法，Wang的算法做對比，表明新算法在保持連通性方面的優勢；在第三個試驗中把新算法與Wang的算法的細化結果做對比，表明新算法具有旋轉不變性；第四個實驗是新算法細化各類模型得到的精準的骨架。

新算法與Ma算法的細化結果對比如圖5所示，在圖5.（a）中是一個連續的簡單模型，圖5.（b）中是Ma算法的細化結果，左右連在一起的兩個方形在細化后被分開，破壞了原有的連通性，圖5.（c）中是新算法的細化結果。左右兩個方形細化后任連在一起，保持了原有的拓撲結構。在圖6.（a）中是一個連續的簡單模型，圖6.（b）中是Ma算法的細化結果，上下連在一起的兩個方形在細化后被分開，破壞了原有的連通性，圖6.（c）中是新算法的細化結果。上下兩個方形細化后任連在一起，保持了原有的拓撲結構

六、結論

完全并行基于模板的細化算法，會出現斷裂，導致細化結果拓撲結構發生改變，并且不具有旋轉不變性，本文通過設計各向同性模板，判斷后刪除點的真偽解決了這一問題，并通過實驗進行了驗證；在三維細化的基礎上實現了非接觸測量，提取三維特征信息，這將進一步滿足對三維模型特征分析的需求。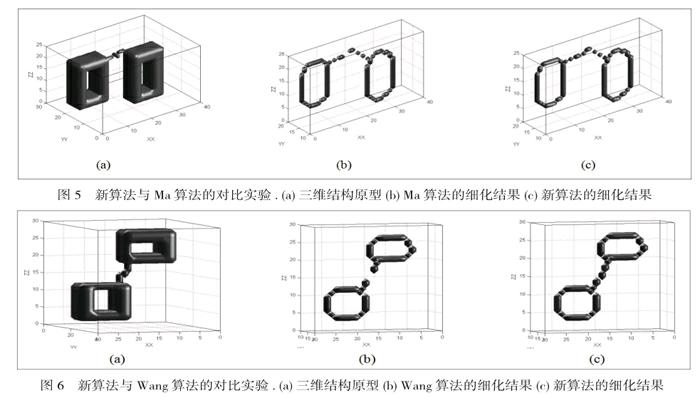

參 考 文 獻

[1]廖開陽，張學冬，章明珠.一種新的指紋圖像快速細化算法[J].計算機工程與應用，2008，44（5）：93-95.

[2]鄧剛，童學鋒.FPTA快速細化算法在脫機手寫體漢子識別中的應用.計算機工程與應用，2002，01：135-136

[3] Chuang JH， Tsai CH， Ko MC. Skeletonization of three-dimensional object using generalized potential field[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2000，22（11）： 1241-1251.

[4]侯培，田慶國，葛寶臻.基于優化DRG的三維人體點云骨架提取算法[J].計算機工程與應用，2014，50（18）：182-187.