基于正交設計的不同墊層落石沖擊力試驗研究

王林峰，唐紅梅，唐　芬，葉四橋

(重慶交通大學 水利水運工程教育部重點實驗室，重慶　400074)

落石是我國常見的一種山地災害，我國山區鐵路、公路等交通設施經常受到落石災害的威脅。

為了防止落石對交通運輸造成嚴重危害，國內外許多學者對落石災害進行了研究。唐紅梅等通過室內模型試驗獲得了落石沖擊信號，并用小波變換對沖擊信號進行消噪，提取了落石的最大沖擊力，然后基于Hertz碰撞理論，通過試驗值反算獲得了土石比在不同密實度下回彈系數的均值和最大值[1]。葉四橋等分析了不同坡面鋪裝、不同坡度、不同下落高度、不同落石質量和形狀試驗條件下落石的運動參數,據此反算法向恢復系數[2]；此外，葉四橋等還通過沖量定理和在日本道路公團算法以及有關試驗數據的基礎上研究新的落石沖擊力計算方法[3]。楊其新等也通過室內試驗提出了落石沖擊力計算經驗公式[4]。Dorren等提出了用于估算墊層上植被減少的落石沖擊能量計算公式，以及考慮斜坡表面障礙物最大高度和落石半徑建立了土體切向動力恢復系數的估算公式[5]。Zamrano建立了大塊落石運動速度的計算公式[6]。Vilajosana等通過1次現場試驗對落石的沖擊信號進行了研究[7]，Pichler等通過室外試驗得到了由落石沖擊坑深度、落石幾何尺寸和落石高度計算落石沖擊力和沖擊時間的計算公式[8]。 CALVETTI等通過室內試驗分析了不同條件下落石棚洞受到的落石沖擊力變化規律[9]。Zhang Guangcheng等通過引入法向和切向恢復系數建立了落石沖擊力計算公式[10]。

落石沖擊力是落石防治工程設計中必須考慮的重要荷載。由于落石和墊層的隨機性，導致通過理論推導建立精確的落石沖擊力計算公式存在較大的難度，特別是受落石下部沖擊墊層的影響更加復雜。本文基于正交設計，通過室內模型試驗，分析不同的落石沖擊高度、墊層黏土含量、墊層傾角、落石重力、壓縮模量和含水量等因素對落石沖擊力的影響，并通過試驗數據建立落石沖擊力計算公式。

1　落石沖擊試驗

本文的不同墊層條件下落石沖擊試驗系統如圖1所示，該試驗系統主要由落石沖擊系統、墊層和數據采集系統3部分組成。落石沖擊系統包含落石、支架和落石沖擊控制系統，落石支架的尺寸為200 cm×200 cm×450 cm；落石沖擊數據用DH3817動態應變儀采集，墊層由不同配比的碎石和黏土制成。

試驗中考慮影響落石沖擊力的因素及選取的工況如下。

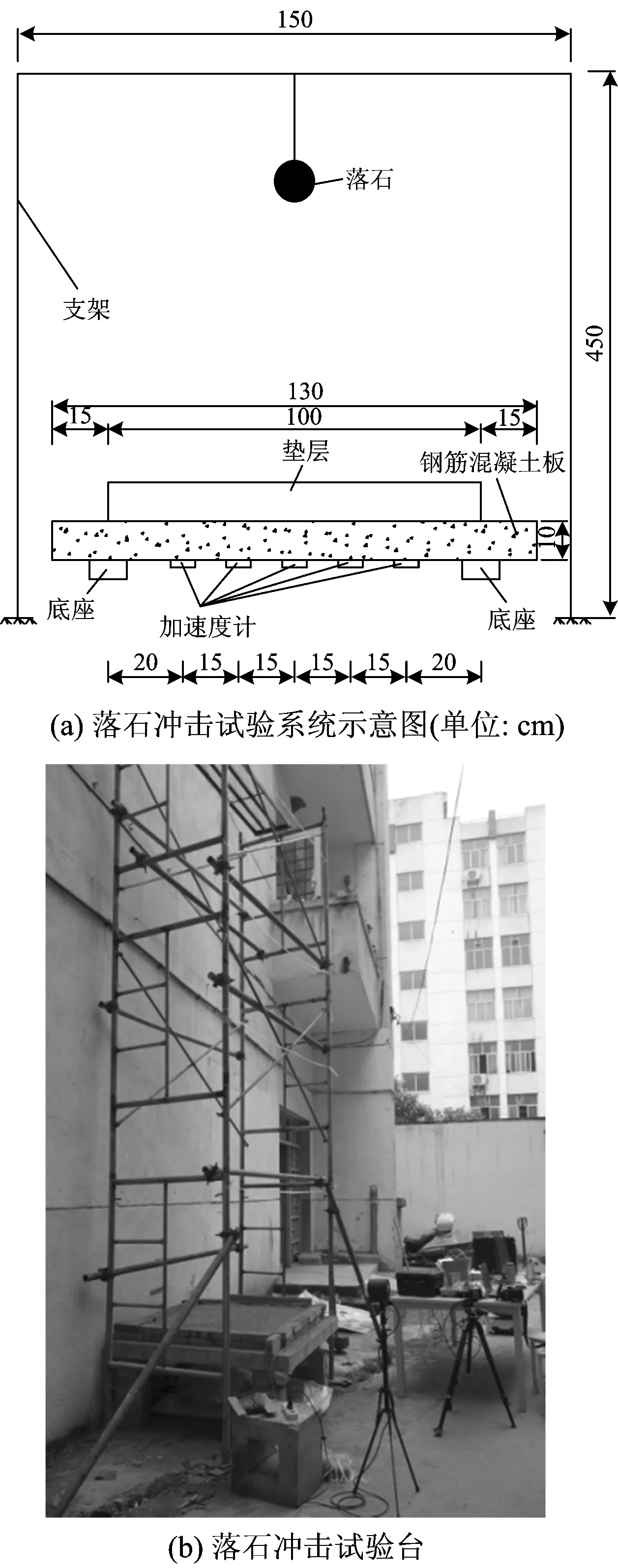
圖1　落石模型試驗系統

(1)落石下降高度，分別為150，200，250和300 cm。

(2)落石重力，分別為30， 50和72.8 N。

(3)墊層，通過碎石和黏土混合而成，黏土含量分別為30%，40%，50%和60%。

(4)墊層傾角，分別為0°，20°，40°和60°。

(5)墊層壓縮模量，分別為26，29，34和38 MPa。

(6)墊層含水量，分別為9.4%，13.7%，16.2%和19.4%。

由以上的試驗方案可知試驗中考慮的因素主要有落石下降高度、黏土含量、墊層傾角，落石重力、墊層含水量和壓縮模量共6個。這6個因素對應的水平除落石重力為3個外，其余均為4個，不同墊層下落石沖擊力試驗因素水平表見表1。

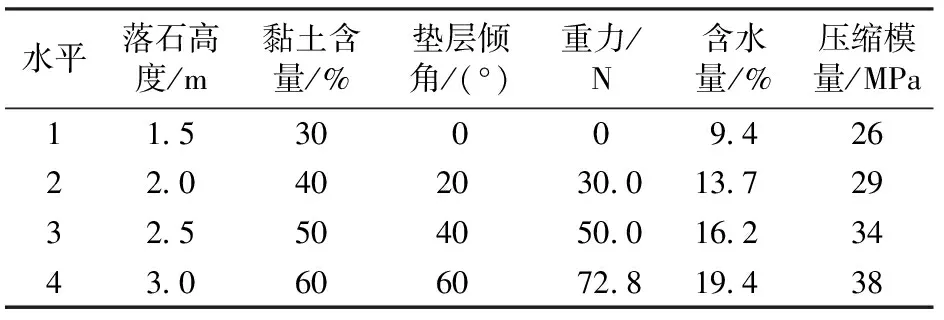
表1　不同墊層落石沖擊力試驗因數水平表

本文選擇L32(49)正交表進行試驗分析[11]。 由于試驗考慮了6個因素，因此用A,B,C,D,E,F分別代表這6個因素做正交試驗，而且對各因素不同水平組合重復做3次試驗。

2　試驗結果及分析

依據表2的組合方式進行落石試驗，得到的落石沖擊力結果見表2。

表2　L32(49)落石沖擊力正交試驗表及試驗結果

2.1　極差分析

對表2的落石沖擊力試驗結果進行極差分析。首先計算各因素在各水平下的沖擊力之合，結果見表3；再計算各因素在各水平下的沖擊力平均值，結果見表4。

由極差的定義可知，極差為各因素沖擊力平均值的最大值與最小值的差，該指標表示某因素作用下沖擊力的變化大小，即該因素對沖擊力的影響大小。由表4的極差值可以看出，落石重力的極差值最大，其次是落石高度的極差值，因此，這6個因素中落石重力對落石沖擊力的影響最大，其次是落石高度。剩下的4個因素對落石沖擊力影響的由大到小的順序為黏土含量、壓縮模量、含水量和墊層傾角。

表3　沖擊力之合

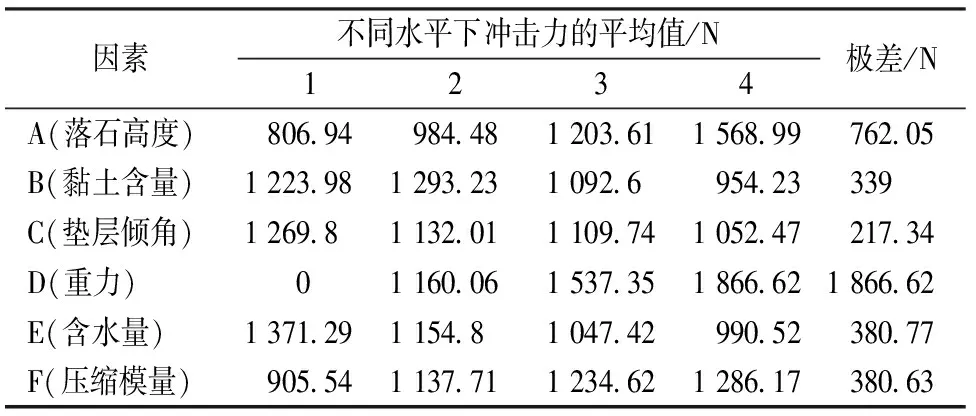
表4　沖擊力的平均值與極差

為了更直觀地比較，根據表4繪制的各因素不同水平下的落石沖擊力如圖2所示。由圖2可得以下結論：

①對于落石高度因素， 3 m時，即A4落石沖擊力最大；

②對于黏土含量因素，40%時，即B2落石沖擊力最大；

③對于墊層傾角因素，0°時，即C1落石沖擊力最大；

④對于落石重力因素，72.8 N時，即D4落石沖擊力最大；

⑤對于墊層含水量因素，9.4%時，即E1落石沖擊力最大；

⑥對于墊層壓縮模量因素，38 MPa時，即F4落石沖擊力最大；

綜合以上各結論，因素組合A4B2C1D4E1F4下的落石沖擊力將會最大。

為了確定組合A4B2C1D4E1F4的沖擊力，單獨實施該組合條件下的試驗，試驗測得該組合條件下落石的沖擊力為3 290 N，比正交試驗中的最大沖擊力增大了26.24%。

由圖2也可以很容易看出各個因素對落石沖擊力影響的主次，在圖中，如果某因素對落石沖擊力的影響很大，那么該因素不同水平下落石沖擊力的差值會很大，即這個因素就是影響落石沖擊力的主要因素，反之如果該因素不同水平下落石沖擊力的差值會很小，即這個因素就是影響落石沖擊力的次要因素。沖擊力的差值在圖2中反映為各因素對應沖擊力點的分布分散程度。

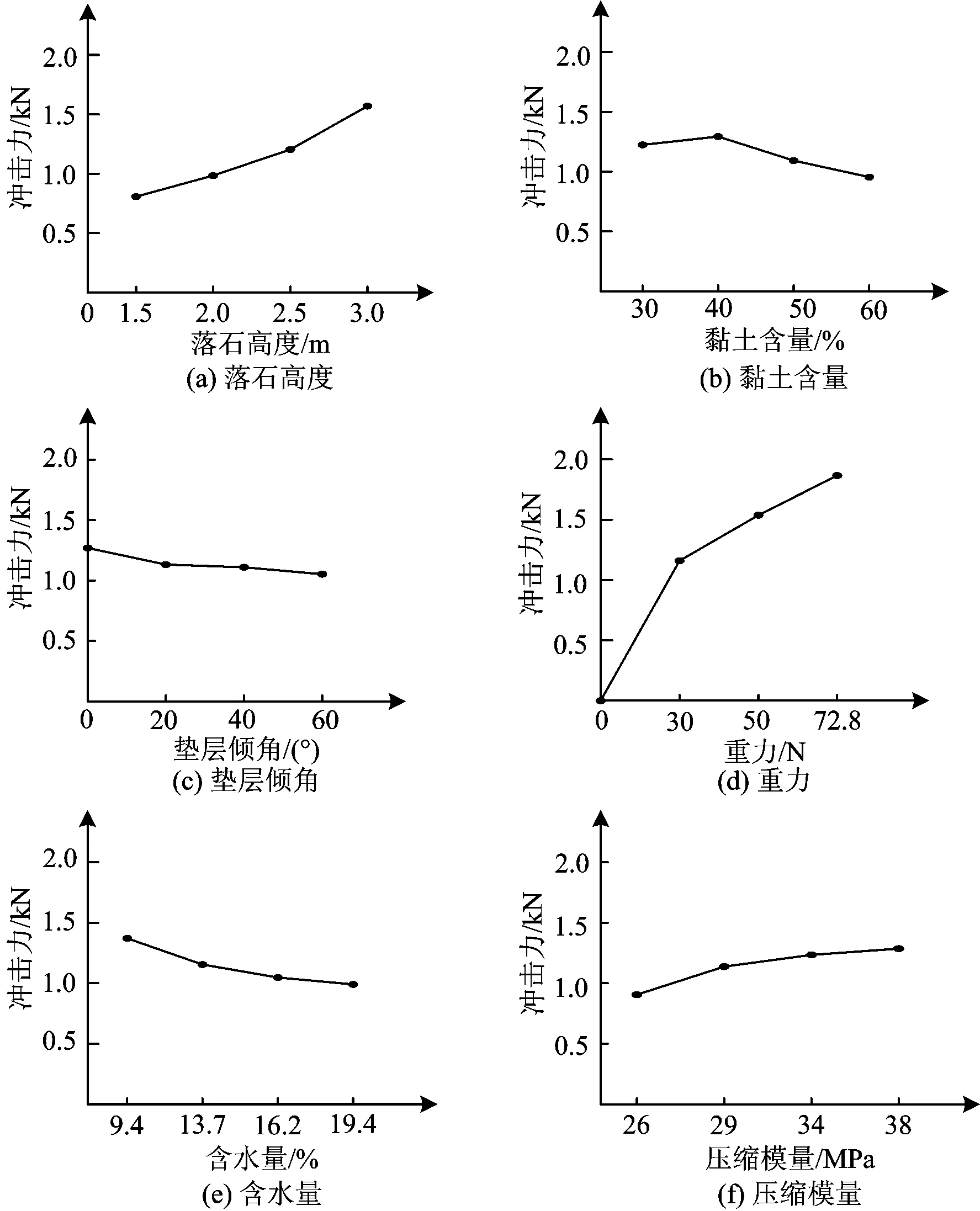
圖2　各因素不同水平下的落石沖擊力

根據以上的規律，從圖2中可見，在影響落石沖擊力的各個因素中，落石重力的點最分散，因此，落石重力為影響落石沖擊力的最主要因素；其次，落石高度的點比較分散，因此，落石高度為影響落石沖擊力的次主要因素；以下依次為黏土含量、壓縮模量、含水量和墊層傾角。即這6個因素對落石沖擊力影響的主次排序為(由主到次)落石重力→落石高度→黏土含量→壓縮模量→含水量→墊層傾角。通過前面的分析發現，不同因素對落石的沖擊力改變量是不同的。鑒于此，可以通過調節敏感因素來減小沖擊力，進而更好地保護落石災害的承災體。

在同一落石災害處，落石的高度和體積是一定的，則落石高度和落石重量可視為定值，且前面的分析已發現墊層傾角對落石的沖擊力影響較小。因此在落石防治結構設計時可以通過調節墊層的黏土含量、壓縮模量和含水量3個因素控制落石沖擊力，3個因素作用下沖擊力達到最小的組合是B4E4F1。

圖3為落石重力為72.8 N，墊層滑水量、壓縮模量和傾角分別為19.4%，26 MPa和0°條件下，落石沖擊力隨著不同黏土含量的變化曲線。由圖3可以看出，隨著黏土含量的增加，落石沖擊力先增大后減小，黏土含量為60%時沖擊力為最小。相對于最大沖擊力，當黏土含量為60%時落石沖擊力減小約23%。

圖3　不同黏土含量下的沖擊力變化曲線

圖4為落石重力為72.8 N，黏土含量、壓縮模量和傾角分別為40%、26 MPa和0°條件下，落石沖擊力隨著不同含水量的變化曲線。圖4表明，隨著墊層含水量的增加，沖擊力逐漸減小，并且含水量開始增大時，落石沖擊力的減小幅度較大。當含水量由9.4%增大到19.4%時，落石沖擊力減小約19%。

圖4　不同含水量下的沖擊力變化曲線

圖5為落石重力為72.8 N，黏土含量、含水量和傾角分別為40%、19.4%和0°條件下，落石沖擊力隨著不同壓縮模量的變化曲線。圖5表明，隨著墊層壓縮模量的增加，沖擊力逐漸增大，并且壓縮模量開始增大時，落石沖擊力的增大幅度較大。當壓縮模量由26 MPa增大到38 MPa時，落石沖擊力減小約21%。

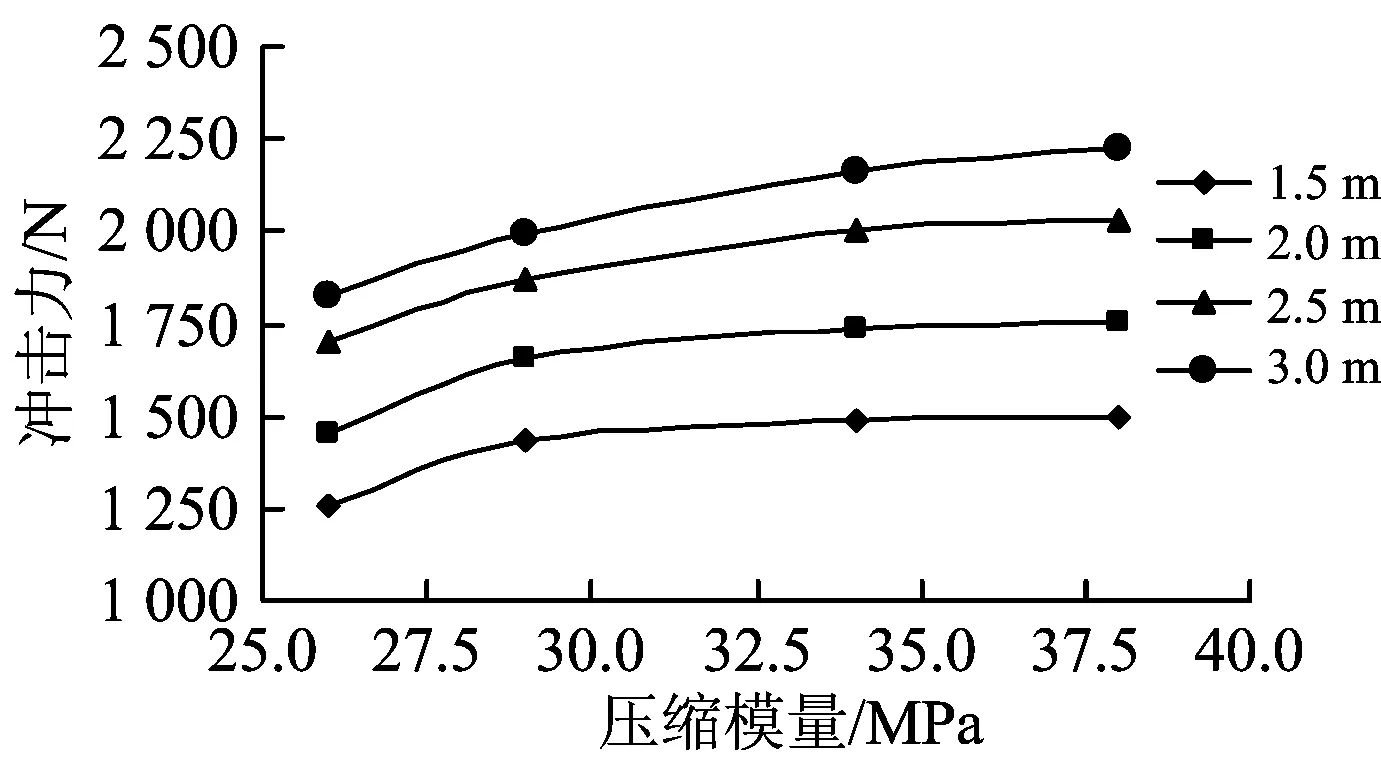
圖5　不同壓縮模量下的沖擊力變化曲線

2.2　顯著性分析

為了精確評估試驗結果誤差的大小，正確區分試驗條件的改變和由試驗誤差二者引起的數據波動，進行試驗考慮的6個因素對落石沖擊力影響的顯著性分析。根據數理統計方法可知，表5中的自由度等于因素水平數減去1；f0.05為顯著水平取0.05時的F檢驗臨界值；f0.01為顯著水平取0.01時的F檢驗臨界值，f0.05和f0.01值可以通過查詢F分布上側分位表獲得。表5中F為組間方差與組內方差的比值，稱為檢驗統計量。

組間方差為

(1)

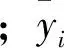
組內方差為

(2)

式中：yij為每次試驗的試驗值。

檢驗統計量F為

(3)

求解出檢驗統計量F后，將其與F檢驗臨界值進行比較，可以判斷出各因素的顯著性。當F值大于f0.05和f0.01值時，表示該因素對試驗結果影響顯著，反之則表示影響不顯著。

由表5可以看出，落石高度和落石重力對落石沖擊力的影響特別顯著，是決定性因素，其次是黏土含量，壓縮模量和含水量，而墊層傾角對落石沖擊力的影響較弱。

表5　顯著性分析表

3　結　論

(1)正交試驗表明，落石重力和落石高度對落石沖擊力的影響特別顯著，6個因素對落石沖擊力影響的主次排序為落石重力→落石高度→黏土含量→墊層壓縮模量→墊層含水量→墊層傾角。

(2)由于在野外落石重力和高度是定值，因此可通過改變墊層的黏土含量、壓縮模量和含水量3個因素控制落石沖擊力，在這3個因素作用下使落石沖擊力達到最小的組合是B4E4F1。調節墊層的黏土含量、壓縮模量和含水量可以分別降低約23%，21%和19%的落石沖擊力。

(3)基于F檢驗的顯著性分析表明，落石高度和落石重力對落石沖擊力的影響非常顯著。

[1]唐紅梅,鮮學福，王林峰,等. 基于小波變換的碎石土墊層落石沖擊回彈系數試驗[J]. 巖土工程學報,2012,34(7):1278-1282.

(TANG Hongmei, XIAN Xuefu, WANG Linfeng, et al. Coefficient of Resilience for Rock Fall onto Gravel Soil Cushion Based on Wavelet Transform Theory[J]. Chinese Journal of Geotechnical Engineering, 2012,34(7):1278-1282. in Chinese)

[2]葉四橋,鞏尚卿. 落石碰撞法向恢復系數的模型試驗研究[J]. 中國鐵道科學,2015,36(4):13-19.

(YE Siqiao, GONG Shangqing.Research on Normal Restitution Coefficient of Rockfall Collision by Model Tests[J]. China Railway Science,2015,36(4):13-19. in Chinese)

[3]葉四橋,陳洪凱,唐紅梅. 落石沖擊力計算方法[J]. 中國鐵道科學,2010,31(6):56-62.

(YE Siqiao,CHEN Hongkai,TANG Hongmei.The Calculation Method for the Impact Force of the Rockfall[J]. China Railway Science, 2010,31(6):56-62. in Chinese)

[4]楊其新,關寶樹.落石沖擊力計算方法的試驗研究[J]. 鐵道學報,1996,18(1):101-106.

(YANG Qixin, GUANG Baoshu.Experiment Study on Rockfall Impact Force Calculate Method[J].Journal of the China Railway Society,1996,18(1):101-106. in Chinese)

[5]DORREN L, BERGER F, PUTTERS U. Real-Size Experiments and 3-D Simulation of Rockfall on Forested and Non-forested Slopes[J]. Natural Hazards and Earth System Sciences, 2006,6(1):145-153.

[6]ZAMBRANO O M. Large Rock Avalanches: A Kinematic Model[J]. Geotechnical and Geological Engineering, 2008,26(3): 283-287.

[7]VILAJOSANA I, SURI E, ABELL A, et al. Rockfall Induced Seismic Signals: Case Study in Montserrat, Catalonia[J]. Natural Hazards and Earth System Sciences, 2008,8：805-812.

[8]PICHLER B, HELLMICH C, MANG H A. Impact of Rocks onto Gravel Design and Evaluation of Experiments[J]. International Journal of Impact Engineering, 2005,31：559-578.

[9]CALVETTI F,PRISCO C. Rockfall Impacts on Sheltering Tunnels: Real-Scale Experiments[J]. Géotechnique,2012,62(10):865-876.

[10]ZHANG Guangcheng,TANG Huiming,XIANG Xin, et al. Theoretical Study of Rockfall Impacts Based on Logistic Curves[J]. International Journal of Rock Mechanics & Mining Sciences,2015,(78)：133-143.

[11]黃潤秋,劉衛華.基于正交設計的滾石運動特征現場試驗研究[J]. 巖石力學與工程學報,2009,28(5):882-891.

(HUANG Runqiu, LIU Weihua. In-Situ Test Study of Characteristics of Rolling Rock Blocks Based on Orthogonal Design[J].Chinese Journal of Rock Mechanics and Engineering, 2009,28(5):882-891. in Chinese)