鋰硫電池模擬與仿真

余聰聰，張　晶，黃成德*

(1.天津大學化工學院，天津 300072； 2.中國電子科技集團第十八研究所，天津 300381)

鋰硫電池是以單質硫為正極、金屬鋰為負極的高能二次電池體系。高達2 600 W·h/kg的理論能量密度，以及硫單質環保、價格便宜等諸多優點，使其受到廣泛關注。目前有關鋰硫電池的研究主要集中于電池的性能提高和模擬仿真2個方向。在模型仿真研究中，盡管Kumaresan[1]、Ghaznavi[2-4]、Fronczek等[5]分別建立了鋰硫電池硫單質連續還原模型并對各個因素，諸如：濃度、沉淀反應速率等對鋰硫電池放電容量的影響進行了系統討論，然而在上述模型中未充分考慮絕緣體——多硫化物沉淀會導致正極活性比表面積損失，造成擬合的前期放電曲線電壓平臺平坦，末期陡降的結果，這與實驗曲線相差甚遠，因此上述的研究尚有待改進。本論文借鑒鋰空電池Li2O2沉淀反應造成多孔碳活性表面積堵塞，在鋰硫電池多硫化物沉淀過程中引入活性反應表面積失效的影響。同時考慮多硫化物形核、生長沉淀過程，完善了鋰硫電池反應模型。

1　模型

1.1　模型建立

鋰硫電池電化學總反應按16Li+S8(s)8Li2S進行，正極為硫單質的多步還原反應[1]。鋰硫電池硫單質S8(l)和多硫離子各分步還原反應以及多硫化物的沉淀反應如表1所示。鋰硫電池模型幾何結構如圖1所示。模擬區間包括金屬鋰負極，多孔碳與硫單質組成的正極，以及多孔隔膜3部分。模型對應的幾何尺寸參數和多硫化物體積分數如表2所示。由于鋰負極相對于硫正極反應速率快，電極過電勢小，因此可忽略其電極厚度對電池反應的影響。模擬區間以鋰負極與隔膜的接觸面為原點開始計算。

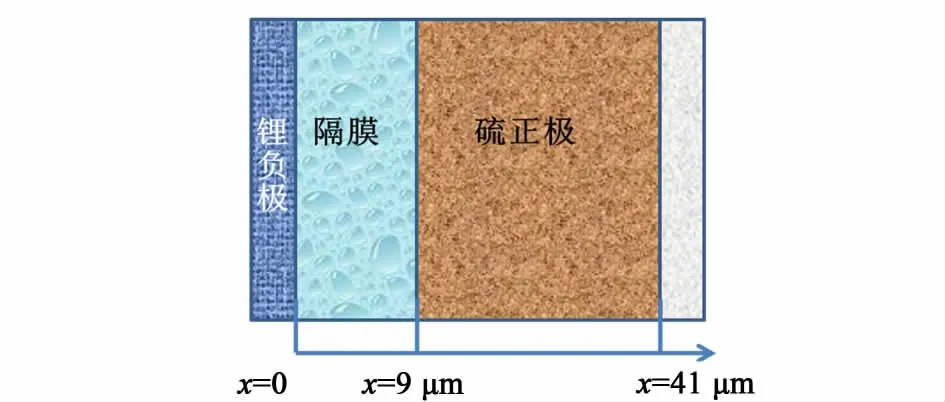
圖1　鋰硫電池模擬區間Fig.1　Schematic of lithium-sulfur cell

反應正極隔膜負極電化學反應(1)Li?Li++e-√(2)1/2S8(l)+e-?1/2S82-√(3)1/2S2-8+e-?2S62-√(4)S2-6+e-?3/2S42-√(5)1/2S2-4+e-?S22-√(6)1/2S2-2+e-?S2-√沉淀與溶解反應(7)S8(s)?S8(l)√√√(8)2Li++S2-8?Li2S8√√√(9)2Li++S2-4?Li2S4√√√(10)2Li++S2-2?Li2S2√√√(12)2Li++S2-?Li2S√√√

1.2　物質傳輸方程

鋰硫電池多孔介質中，包括各物質的質量守恒方程如式(1)所示。

(1)

表2　幾何尺寸參數和多硫化物體積分數[1]Table 2　Separator and cathode parameters[1]

以及對應的各物質通量如式(2)所示。

Ni=-Di,0εbφl

(2)

各物質體相溶液的擴散系數為Di,0，分別由b=1.5進行修正，以反映多孔電極孔隙率和曲折度對各物質傳遞的影響。其中各物質的擴散系數與參考濃度如表3所示。電化學反應(1)～(6)中，各物質生成或者消耗的速率可表示為:

(3)

Ri表示為為沉淀/溶解反應速率，均作為式(1)中的來源項。

表3　擴散系數與參考濃度[2]Table 3　Transport properties and reference concentrations[2]

1.3　質子和電子守恒方程

液相電流密度由各帶電粒子流量乘以所帶電荷得到，如式(4)所示。

(4)

固相電流密度遵循歐姆定律，如式(5)所示。

is=-σφs

(5)

電荷離開或者進入液相都是基于電極電化學反應。因此，固液界面對應的界面電流密度傳輸為:

·il=a∑jij

(6)

以及對應的電荷守恒，如式(7)所示。

is+il=0

(7)

1.4　電化學動力學方程

鋰硫電池中各物質電化學反應電流密度可由濃度修正的Butler-Volmer方程表示，如式(9)所示。

(8)

反應過電勢為：

ηj=φs-φl-Uj,ref

(9)

因為各物質初始濃度并不是標準活性物質濃度，Uj,ref由式(10)進行修正。鋰硫電池各反應的熱力學與動力學參數如表4所示。

(10)

1.5　化學動力學方程

鋰硫電池多硫化物的沉淀反應和正極固體硫單質的溶解反應由(11)式表示。

(11)

沉淀/溶解反應速率，如式(12)所示。

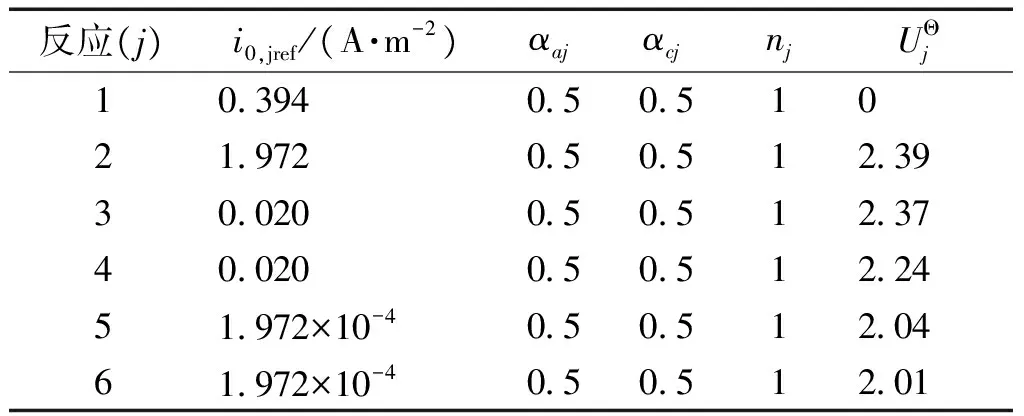
表4　熱力學與動力學參數[1]Table 4　Kinetic and thermodynamic properties[1]

(12)

各多硫化合物沉淀體積分數變化為

(13)

電極孔隙率變化可由(14)式表示。

(14)

鋰硫電池硫單質和多硫化合物的溶解/沉淀反應參數如表5所示。

表5　溶解與沉淀反應參數[2]Table 5　Parameters for precipitation reactions[2]

鋰硫電池反應比表面積由(15)式和(16)式表示。

(16)

其中，ξ用于描述多硫化物形貌系數對電化學反應活性比表面積的影響。a0為正極初始比表面積，ε0為正極初始孔隙率。εprep為多硫化物沉淀體積分數，εinit為活性比表面積完全失效時多硫化物沉淀體積分數。

式(15)反映正極由于S8(s)的溶解和多硫化物的沉淀導致孔隙率變化，引起電極活性比表面積變化。鑒于以往的研究結果不能反映真實的鋰硫電池放電曲線，引入微觀-宏觀均相模型[6](micro-macro homogeneous model)，多硫化物的沉淀使多孔碳活性表面積堵塞，造成活性反應表面積失效的影響[7]。同時結合鋰/亞硫酰氯電池的LiCl沉淀模型[8]，使用誤差函數erf(x)來模擬具有絕緣性質的多硫化物沉淀反應對電極活性比表面積的影響。本文采用式(16)加大了多硫化合物沉淀對電極活性比表面積的影響，完善了多硫化物沉淀過程，以此來優化沉淀反應對鋰硫電池放電性能的影響。

1.6　邊界條件

鋰硫電池邊界條件設定如下：正極邊界條件

Ni=0,is=Iapp,il=0

(17)

隔膜與正極/負極邊界條件

Ni,sep=Ni,cat/anode

(18)

il,sep=il,cat/anode=|Iapp|

(19)

負極邊界條件

(20)

2　結果與討論

2.1　模型驗證

采用商業化COMSOL Multiphysics 4.3b數值模擬軟件，構建偏微分方程來描述鋰硫電池反應的物理現象。本論文擬合了放電倍率分別為0.1 C，0.2 C和0.5 C的放電曲線，結果如圖2a)所示。從圖2a)可看到，放電曲線出現2段，特別是放電末期出現了明顯的電壓降，擬合結果與Yang等[9]的實驗數據相符。由于放電電流密度增加導致歐姆壓降增大，電壓平臺末期會出現下降。同時，導致鋰硫電池放電容量衰減。圖2b)為采用Kumaresan等[1]的活性比表面積表達式(15)，與本研究修正的活性比表面積表達式(16)得到的不同倍率放電曲線對比圖。按式(15)的擬合結果與Kumaresan等[1]研究結果一致。這表明，由于未充分考慮活性表面積被絕緣體——多硫化物覆蓋，正極活性面積大量減少的影響，鋰硫電池反應末期出現了電壓垂直下降，與前述的實際放電曲線不符。這可能是由于固體S8的溶解，造成該方程中孔隙率ε數值在計算中從初始值0.78增加到0.94，最后只下降到0.64。ε在整個放電過程中維持較大數值，沉淀反應對活性表面積a前后變化影響不大，以致式(15)未準確反映活性比表面積損失。在實際情況下，固體S8的絕緣性，造成電極活性反應比表面積應主要與導電多孔碳的比表面積有關。因此，從圖2b)可以看出，本研究采用式(16)，修正鋰硫電池沉淀反應導致活性面積損失的影響，計算結果符合實驗數據，模型更符合鋰硫電池的實際情況。

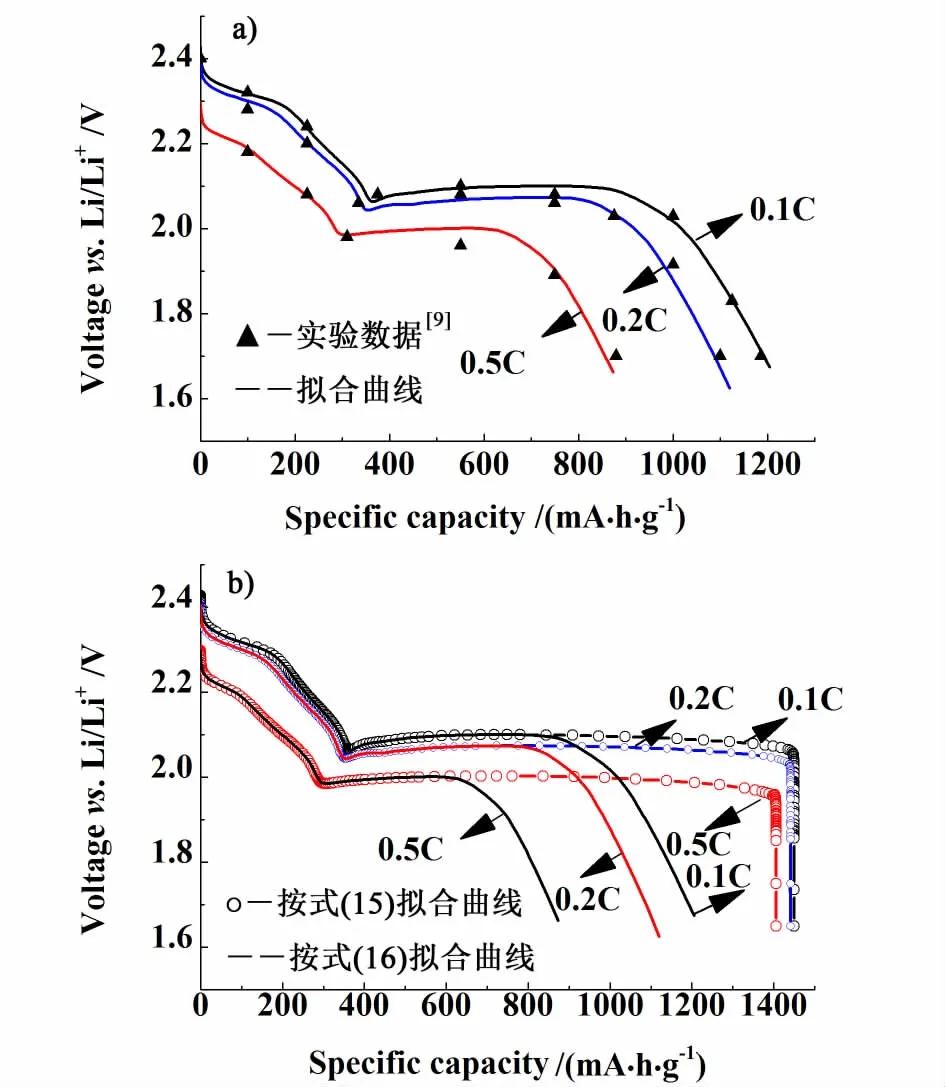
圖2　鋰硫電池的不同倍率放電曲線擬合曲線Fig.2　The discharge curves of lithium-sulfur cell at different discharge current rate

2.2　多硫化物生長速率kG對沉淀反應的影響

分別選取放電倍率為0.1 C和0.5 C，研究Li2S2和Li2S不同生長速率kG對鋰硫電池放電曲線的影響，擬合結果如圖3所示。

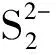
從圖3b) 和圖3d)可看到， Li2S不同生長速率kG對鋰硫電池放電容量的變化影響不大。同時Li2S較大的生長速率kG有利于第2階段放電電壓平臺的提高，甚至電壓平臺出現拐點，但對第1階段放電電壓平臺無影響。該現象與鋰硫電池采用不同鋰鹽的電解質溶液對應的放電實驗數據[10]表現一致。因此，上述放電實驗數據中第2階段初始放電電壓平臺出現一定程度提高的現象，可能與其選用的電解質溶液有利于Li2S沉淀有關。從圖3b) 和圖3 d)擬合結果還可看出， Li2S較小的生長速率kG會使得第2階段放電電壓平臺出現一定坡度的下降。特別是在0.5 C放電倍率下，出現了電壓平臺向下滑移和放電容量減小。Mikhaylik的實驗結果[10]顯示，較低溫度下，第1階段放電電壓平臺對應的放電容量反而要大于常溫下鋰硫電池的放電容量。出現這種現象的原因很可能是低溫條件Li2S較小的生長速率kG導致了第2階段電壓平臺向下滑移，從而使得第1階段放電容量有所增大。

2.3　多硫化物形核速率kN對沉淀反應的影響

分別選取放電倍率為0.1 C和0.5 C，研究Li2S2和Li2S不同形核速率kN對鋰硫電池放電曲線的影響，擬合結果如圖4所示。

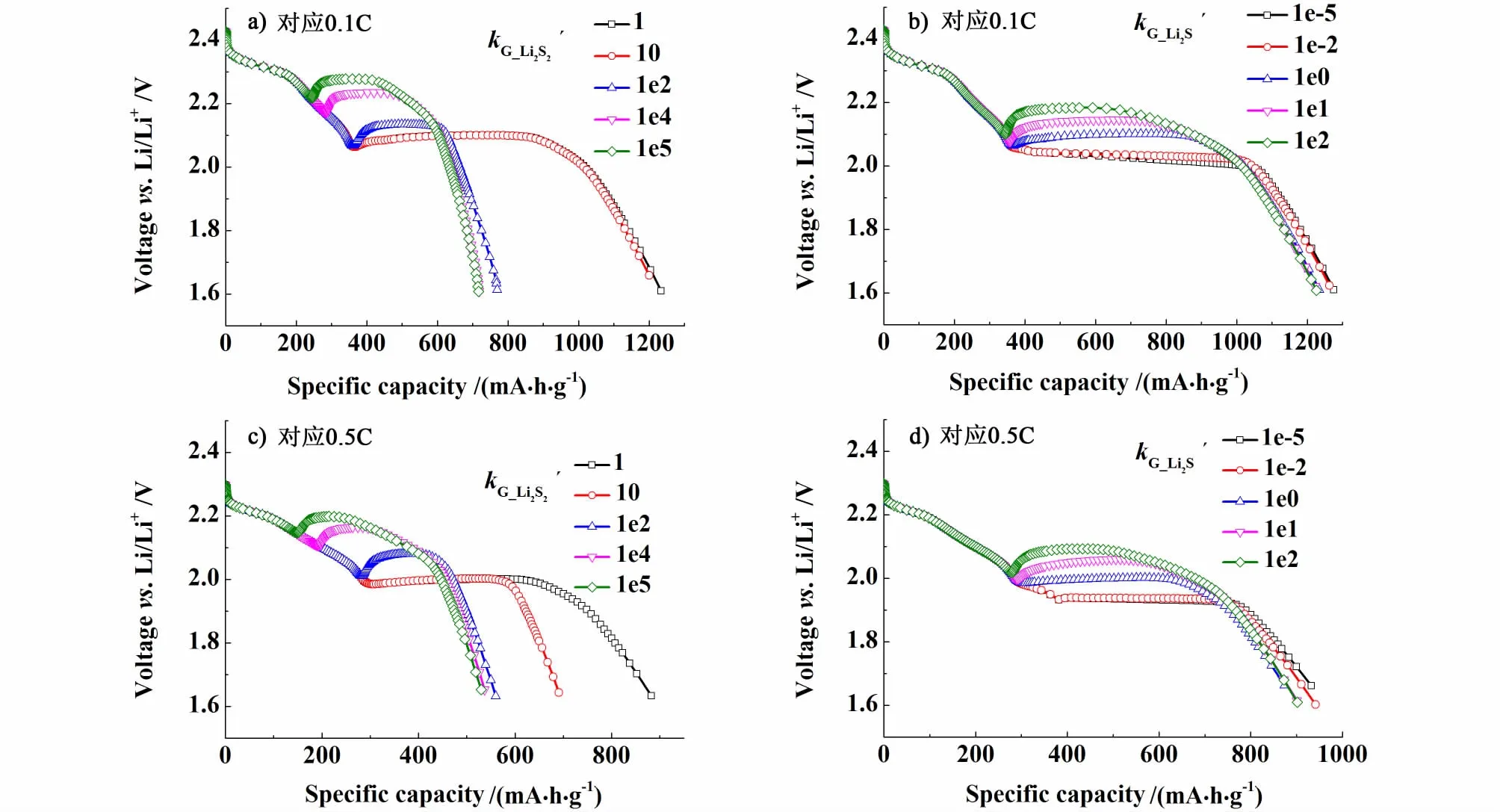
圖3　鋰硫電池中Li2S2和Li2S不同生長速率kG對應0.1 C和0.5 C放電曲線Fig.3　The discharge curves of lithium-sulfur cell for different growth rate constants of Li2S2 and Li2Sat 0.1 C and 0.5 C

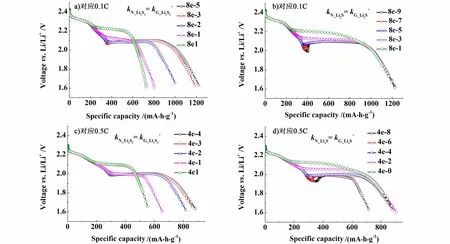
圖4　鋰硫電池中Li2S2和Li2S不同形核速率kN對應0.1 C和0.5 C放電曲線Fig.4　The discharge curves of lithium-sulfur cell for different nucleation rate constants of Li2S2 and Li2Sat 0.1 C and 0.5 C

模擬結果顯示，由方程(12)得知多硫化物生長速率kG與沉淀物體積分數成比例，故較小的多硫化物體積分數使得在沉淀反應初期形核速率kN占主導地位，形核速率kN對放電曲線的影響在沉淀反應初期要大于生長速率kG。由圖4a)和圖4c)可以看出，Li2S2形核速率kN對放電曲線的影響與其生長速率kG類似，較大的Li2S2生長速率kG，同樣會造成鋰硫電池放電電壓平臺升高和放電容量衰減。而由圖4c)和圖4 d)可以看出，Li2S較大的形核速率kN，使得第2階段電壓平臺有所提高，同時縮小了第1階段的放電容量，這與其生長速率kG對應的影響有所不同。比較圖3和圖4可知，較快的形核速率會導致放電曲線在200～450 mA·h·g-1之間出現拐點，其擬合曲線與Ghaznavi模擬結果[3]相吻合。

2.4　多硫化物沉淀形貌系數m對沉淀反應的影響

分別選取放電倍率為0.1 C和0.5 C，研究Li2S2和Li2S沉淀形貌系數m[見式(12)指數項]對鋰硫電池放電曲線的影響，擬合結果如圖5所示。

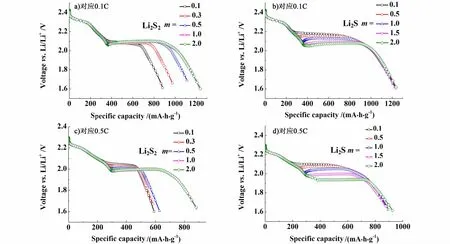
圖5　鋰硫電池中Li2S2和Li2S沉淀形貌系數m對應0.1 C和0.5 C放電曲線Fig.5　The discharge curves of lithium-sulfur cell for different morphological parameters of Li2S2 and Li2Sat 0.1 C and 0.5 C

當鋰硫電池充分反應時，多硫化物主要以Li2S2和Li2S形式存在[3]。本研究主要研究了沉淀形貌系數m對Li2S2和Li2S沉淀反應以及對應放電曲線的影響。沉淀形貌系數m表現為多硫化物在活性表面積上的沉淀形貌，較小的m值意味著多硫化物沉淀更加均勻、平坦，而較大的m值類似針狀沉淀，沉淀效果較差[6]。由圖5a)和圖5c)可知，隨著沉淀形貌系數m變小，Li2S2沉淀反應速率加快，擬合結果與Li2S2不同形核速率kN對鋰硫電池放電性能的影響類似，放電容量減小，放電電壓平臺略有升高。同時，在較大放電倍率條件下，m的大小對Li2S2沉淀反應的影響增大，放電容量衰減程度加大。由圖5b)和圖5 d)可知，Li2S沉淀形貌系數m的大小對鋰硫電池放電容量影響不大，但對電壓平臺高低變化有較大影響。較小的m沉淀效率更高，加快了Li2S沉淀體積分數對kG的影響，有利于提高電壓平臺。而較大的m導致Li2S沉淀速率降低，特別是造成大電流放電電壓平臺下降明顯。因此，選擇適宜的有機電解質溶液提高多硫化物沉淀速率有利于提高鋰硫電池放電平臺和放電容量。

3　結論

使用COMSOL Multiphysics建立了鋰硫電池數值模型，著重修正了原有模型因為對活性比表面積變化考慮不足，造成鋰硫電池放電性能預測不準確的影響。通過與實驗數據對比，模擬放電曲線和實驗結果吻合，驗證了模型的正確性，利用該模型可得到以下結論。

1)多硫化物沉淀過程造成電極活性比表面積大量減少，是鋰硫電池放電性能降低的主要原因。通過誤差函數erf(x)來表示活性比表面積變化，以及采用形核-生長沉淀模型能夠準確的模擬鋰硫電池放電過程。

2)由于多硫化物的絕緣性和沉淀反應都會造成鋰硫電池活性比表面積逐漸減少，放電性能逐漸降低。原有模型假設不準確的原因在于固體硫的溶解會使得電極孔隙率增大，而孔隙率ε主要表現為電解液的空間體積分數，更多的是影響電解液傳輸性質。

3)Li2S較大的生長速率kG和形核速率kN均有利于鋰硫電池第2階段放電電壓平臺和放電容量的提高。Li2S2較大的生長速率kG和形核速率kN在提高第2階段放電電壓平臺的同時，會壓縮第1階段放電電壓平臺，同時造成放電容量衰減。Li2S2沉淀形貌系數m減小，會使Li2S2沉淀反應速率加快，放電容量減小，放電電壓平臺略有升高。而Li2S沉淀形貌系數m的大小對鋰硫電池放電容量影響不大，但對電壓平臺高低變化有較大影響。

符號說明：

a—正極比表面積；

a0—正極初始比表面積；

b—Bruggeman系數；

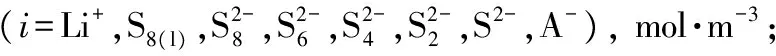
Di,0—物質i體相擴散系數, m2·s-1；

F—法拉第常數, 96485 C·mol-1；

ij—反應j電流密度, A·m-2；

il—液相表面電流密度, A·m-2；

is—固相表面電流密度, A·m-2；

Ksp—多硫化物溶度積；

kG—生長速率常數；

kN—形核速率常數；

m—多硫化物形貌系數對沉淀反應[式(12)]的影響；

ξ—多硫化物形貌系數對電化學反應[式(15)]的影響；

σ—正極固相有效電導率, S·m-1；

ηj—電化學反應j過電勢；

φs—固相電勢, V；

φl—液相電勢, V；

αaj—反應j陽極傳輸系數；

αcj—反應j陰極傳輸系數；

Zi—物質i電荷數；

Vk—多硫化物k摩爾體積分數, m3·mol-1；

ri—物質i基于電化學反應的反應速率, mol·m-3·s-1；

Ri—物質i基于沉淀反應的反應速率, mol·m-3·s-1；

sij—物質i基于電化學反應的化學計量系數；

nj—電化學反應電荷傳輸個數；

T—鋰硫電池溫度；

ε—正極和隔膜孔隙率；

ε0—正極初始孔隙率；

εk—正極和隔膜多硫化物沉淀體積分數；

εprep—多硫化物沉淀體積分數；

εinit—活性比表面積完全失效時多硫化物沉淀體積分數。

參考文獻：

[1]Kumaresan K, Mikhaylik Y, White R E. A mathematical model for a lithium-sulfur cell[J]. Journal of The Electrochemical Society, 2008, 155(8): A576-A582

[2]Ghaznavi M, Chen P. Sensitivity analysis of a mathematical model of lithium-sulfur cells part I: Applied discharge current and cathode conductivity[J]. Journal of Power Sources, 2014, 257: 394-401

[3]Ghaznavi M, Chen P. Sensitivity analysis of a mathematical model of lithium-sulfur cells: Part II: Precipitation reaction kinetics and sulfur content[J]. Journal of Power Sources, 2014, 257: 402-411

[4]Ghaznavi M, Chen P. Analysis of a mathematical model of lithium-sulfur cells Part III: Electrochemical reaction kinetics, transport properties and charging[J]. Electrochimica Acta, 2014, 137: 575-585

[5]Fronczek D N, Bessler W G. Insight into lithium-sulfur batteries: Elementary kinetic modeling and impedance simulation[J]. Journal of Power Sources, 2013, 244: 183-188

[6]Sahapatsombut U, Cheng H, Scott K. Modelling the micro-macro homogeneous cycling behaviour of a lithium-air battery [J]. Journal of Power Sources, 2013, 227: 243-253

[7]Xue K, Nguyen T K, Franco A A. Impact of the cathode microstructure on the discharge performance of lithium air batteries: A multiscale model [J]. Journal of the Electrochemical Society, 2014, 161(8): E3 028-E3 035

[8]Tsaur K C, Pollard R. Precipitation of solids in electrochemical cells[J]. Journal of the Electrochemical Society, 1986, 133(11): 2 296-2 308

[9]Yang Y, Yu G, Cha J,etal. Improving the performance of lithium sulfur batteries by conductive polymer coating [J]. ACS, 2011, 5(11): 9 187-9 193

[10]Mikhaylik Y V, Akridge J R. Low temperature performance of Li/S batteries[J]. Journal of the Electrochemical Society, 2003, 150(3): A306-A311