互聯(lián)網(wǎng)迷因傳播模型的構建與仿真：以“友誼的小船”為例

張頔

摘 要 論文基于個體對互聯(lián)網(wǎng)迷因的創(chuàng)新行為，在傳統(tǒng)SIR模型中引入創(chuàng)新者人群，構建互聯(lián)網(wǎng)迷因傳播模型SIInR。研究發(fā)現(xiàn)在高感染率、接觸率，低恢復率、創(chuàng)新率、免疫率的情況下，互聯(lián)網(wǎng)迷因的發(fā)展趨勢更穩(wěn)定持久。

關鍵詞 互聯(lián)網(wǎng)迷因 SIR模型傳播 SIInR模型

分類號 G250.7

DOI 10.16810/j.cnki.1672-514X.2017.03.012

The Construction and Simulation of Internet Meme Model：A Case Study of “Friendship Boat”

Zhang Di

Abstract Based on the individuals innovation behavior of Internet meme， this paper builds Internet memes propagation model SIInR by extending the classical SIR model with innovative populations. It finds that Internet memes with high rates of infection and contact， low rates of recovery， innovation and immunization will be more stable and lasting.

Keywords Internet memes. SIR model. SIInR model.

迷因（Meme），是Dawkins1976年在《自私的基因》一書中創(chuàng)造，定義為文化基因，它通過大腦復制、進化和傳播，影響人類思想的傳承和發(fā)展。Web2.0環(huán)境促進了迷因的發(fā)展，它是一種具有傳染力的網(wǎng)絡文化片段，通過個體的模仿和創(chuàng)新行為，在短時間內(nèi)病毒式傳播并獲得影響力[1-4]。互聯(lián)網(wǎng)迷因常見的表現(xiàn)形式有詞組、語句、圖像及視頻。

目前，國內(nèi)學者對Meme一詞有多種譯法，直譯的有謎米、冪姆、覓母、敏母、迷因等，譯意的有文化因子、擬子、理念因子等。其中使用頻率較高的譯法為語言學家何自然提出的“模因”，模仿符合Meme的基本特征[5]。對于互聯(lián)網(wǎng)迷因的研究內(nèi)容，國內(nèi)研究者多集中于語言學的語用、翻譯、語言教學等基礎研究[6-9]。本文為了區(qū)別于語言學，采用“迷因”的譯法，討論互聯(lián)網(wǎng)迷因在計算機科學、傳播學中，對互聯(lián)網(wǎng)文化的促進或抑制作用。

1 互聯(lián)網(wǎng)迷因的研究方式

互聯(lián)網(wǎng)迷因因具有高速復制、快速滲透、傳播變異的特點，大量個體的模仿、創(chuàng)新行為促進了互聯(lián)網(wǎng)迷因的不斷發(fā)展。國外研究者將互聯(lián)網(wǎng)迷因與計算機科學、社會心理學、傳播學等多學科交叉研究，提供了多種建模案例，如時間序列模型[10-13]、復雜網(wǎng)絡傳播模型[14-16]、競爭模型[17-19]等。自Brodie提出互聯(lián)網(wǎng)迷因是一種類似于病毒的事物后[20]，研究者開始采用傳染病及其拓展模型分析互聯(lián)網(wǎng)迷因的傳播模式，研究方式主要分為以下三種：

第一種，采用傳統(tǒng)傳染病模型研究互聯(lián)網(wǎng)迷因的傳播過程。Wang采用SIR模型建模，提出互聯(lián)網(wǎng)迷因是一種具有傳染性的實體，傳播初期出現(xiàn)尖峰特點，中后期呈現(xiàn)出逐漸下降的狀態(tài)[21]；Towers采用對比實驗方式研究視頻型互聯(lián)網(wǎng)迷因的傳播率，發(fā)現(xiàn)SIR模型能良好檢測迷因在傳播過程中的促進或抑制作用[22]；Freitag從新聞網(wǎng)站、公眾論壇中獲取4.6億字的在線語料庫，討論語句型互聯(lián)網(wǎng)迷因的結(jié)構形成過程，發(fā)現(xiàn)標準SIR模型能良好模擬互聯(lián)網(wǎng)迷因的歷史發(fā)展狀態(tài)，可用于預測新互聯(lián)網(wǎng)迷因的發(fā)展趨勢[23]。第二種，改進傳統(tǒng)傳染病模型。Bauckhage從Youtube中收集了800個視頻型互聯(lián)網(wǎng)迷因，在SIR模型基礎上引入Markov隨機游走過程，討論個體通過社交關系分享視頻后的動態(tài)觀注率[24]；Weng結(jié)合個體在社群中的結(jié)構位置，研究互聯(lián)網(wǎng)迷因在傳播過程中的擴散阻礙關系，從早期的傳播格局預測未來的傳播路徑[25]；Wei研究互聯(lián)網(wǎng)迷因在不同網(wǎng)絡結(jié)構中的競爭差異性，采用SIS模型確定互聯(lián)網(wǎng)迷因傳播的關鍵位置，并以SI2S模型擬合競爭迷因的傳染過程，反映真實復合網(wǎng)絡中互聯(lián)網(wǎng)迷因的相互作用關系[26，27]。第三種，根據(jù)現(xiàn)實情形構建新傳染病模型。Zhao研究群體的遺忘機制、記憶機制對信息傳播的影響，在傳統(tǒng)SIR模型中加入冬眠者（Hibernators），構建SIHR模型[28]；Rocha從神經(jīng)生物學角度研究互聯(lián)網(wǎng)迷因的傳播過程，在SIR模型基礎上提出社會認知模型，用于解釋互聯(lián)網(wǎng)迷因的動態(tài)傳播現(xiàn)象[29]。綜上所述，傳染病及其拓展模型能有效闡釋信息的傳播機理、預測未來的流行趨勢，為政府監(jiān)管部門的防控決策提供理論依據(jù)。

然而，當以互聯(lián)網(wǎng)迷因作為研究對象時，上述模型僅從信息傳播角度研究互聯(lián)網(wǎng)迷因的傳播模式，缺少了對互聯(lián)網(wǎng)迷因本質(zhì)特性的考量。因而，本文基于個體創(chuàng)新行為，在傳統(tǒng)SIR模型基礎上引入創(chuàng)新者群體，構建SIInR（Susceptible、Infected、Innovative、Recovered）互聯(lián)網(wǎng)迷因傳播模型，討論模型的無病平衡點DFE，分析感染率、恢復率、創(chuàng)新率、接觸率及免疫率對互聯(lián)網(wǎng)迷因的發(fā)展趨勢的影響，并以語句型互聯(lián)網(wǎng)迷因“友誼的小船”實例仿真。

2 互聯(lián)網(wǎng)迷因傳播模型SIInR的構建

2.1 SIInR模型的構建

在傳統(tǒng)無生命動力學SIR模型中，假設系統(tǒng)群體的總?cè)丝跀?shù)不受出生率、死亡率的影響，恒定為一個常數(shù)，并將群體劃分為易感者（Susceptible）、感染者（Infected）及免疫者（Recovered）三類互不交叉人群，討論在病毒刺激下系統(tǒng)群體的狀態(tài)轉(zhuǎn)變。本文將互聯(lián)網(wǎng)迷因看作系統(tǒng)中的病毒，考慮到現(xiàn)實世界中個體對互聯(lián)網(wǎng)迷因的創(chuàng)新行為，在無生命動力學SIR模型基礎上，加入創(chuàng)新者人群（Innovative），構建SIInR互聯(lián)網(wǎng)迷因傳播模型。

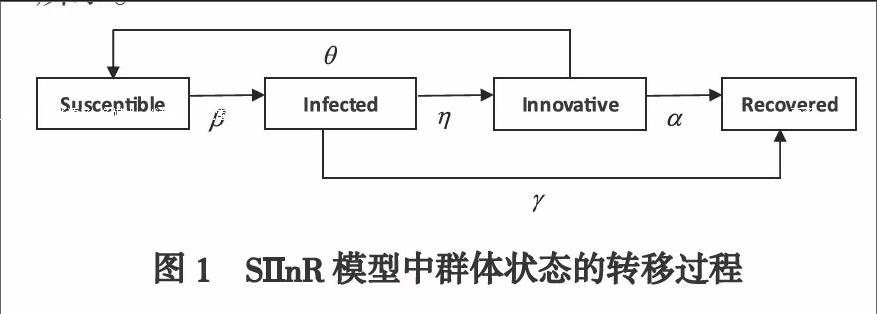
假設SIInR模型中群體人口總數(shù)恒定為一個常數(shù)，將群體劃分為易感者（Susceptible）、感染者（Infected）、創(chuàng)新者（Innovative）及免疫者（Recovered）四類互不交叉的人群，對應到現(xiàn)實世界，則分別為：未接收到互聯(lián)網(wǎng)迷因的易感者S、收到并對互聯(lián)網(wǎng)迷因產(chǎn)生興趣的感染者I、創(chuàng)新互聯(lián)網(wǎng)迷因的創(chuàng)新者In以及對互聯(lián)網(wǎng)迷因不感興趣的免疫者R。當互聯(lián)網(wǎng)迷因刺激系統(tǒng)時，群體的狀態(tài)會發(fā)生轉(zhuǎn)變，如圖1所示。

圖1 SIInR模型中群體狀態(tài)的轉(zhuǎn)移過程

群體狀態(tài)的具體轉(zhuǎn)移過程為：

①S→I：當互聯(lián)網(wǎng)迷因刺激系統(tǒng)后，易感者以β概率成為對互聯(lián)網(wǎng)迷因感興趣的感染者，β代表感染率；

②I→R：感染者經(jīng)過一段時間后，以？酌概率對互聯(lián)網(wǎng)迷因失去興趣成為免疫者，？酌表示恢復率；

③I→In：感染者在對互聯(lián)網(wǎng)迷因感興趣的同時，以？濁概率模仿及創(chuàng)新互聯(lián)網(wǎng)迷因成為創(chuàng)新者，？濁表示創(chuàng)新率；

④In→S：創(chuàng)新者以？茲概率將創(chuàng)新后的互聯(lián)網(wǎng)迷因傳播給易感者，？茲表示接觸率；

⑤In→R：創(chuàng)新者不傳播創(chuàng)新后的互聯(lián)網(wǎng)迷因，經(jīng)過一段時間后，以？琢概率變成免疫者，？琢表示免疫率。

本文使用S（t）、I（t）、In（t）及R（t）分別代表在t時刻不同群體在系統(tǒng)中所占的比例，則SIInR模型的微分方程可用公式（1）表示：

■=-βSI+θIn

■=βSI-（？酌+？濁）I

■=？濁I-（？琢+？茲）In

■=？酌I+？琢In（1）

其中，感染率β、恢復率？酌、創(chuàng)新率？濁、接觸率及免疫率？琢的取值范圍均為[0，1]，且滿足S（t）+I（t）+In（t）+R（t）=1。

2.2 SIInR模型的無病平衡點DFE

研究者指出傳染病及其拓展模型均存在無病平衡點DFE（Disease Free Equilibrium），DFE是模型系統(tǒng)的傳播閾值，包括零傳播平衡點及內(nèi)部平衡點兩種類型，通常用R0表示[30-32]。當R0<1時，穩(wěn)定的DFE使病毒不能侵入模型系統(tǒng)，群體狀態(tài)不發(fā)生轉(zhuǎn)變；當R0=1時，病毒的傳染能力達到系統(tǒng)群體感染的最小值；當R0>1時，DFE的不穩(wěn)定性使病毒可以侵入模型系統(tǒng)中，導致群體狀態(tài)發(fā)生變化。

對于本文提出的SIInR模型，由于零傳播平衡點是一種理想狀態(tài)，在現(xiàn)實世界中無明顯意義，因此本文重點討論SIInR模型的內(nèi)部平衡點。根據(jù)傳播動力學理論計算模型系統(tǒng)的無病平衡點[33]，公式（1）中前3個方程不含變量R，因此先將微分方程轉(zhuǎn)化為公式（2）：

■=-βSI+θIn

■=βSI-（？酌+？濁）I

■=？濁I-（？琢+？茲）In（2）

令x=（I，In，S）T，則公式（2）可表示為■=F（x）-V（x），其中：

F（x）=βSI 0 0 V（x）=（？酌+？濁）I-？濁I+（？茲+？琢）In βSI-？茲In（3）

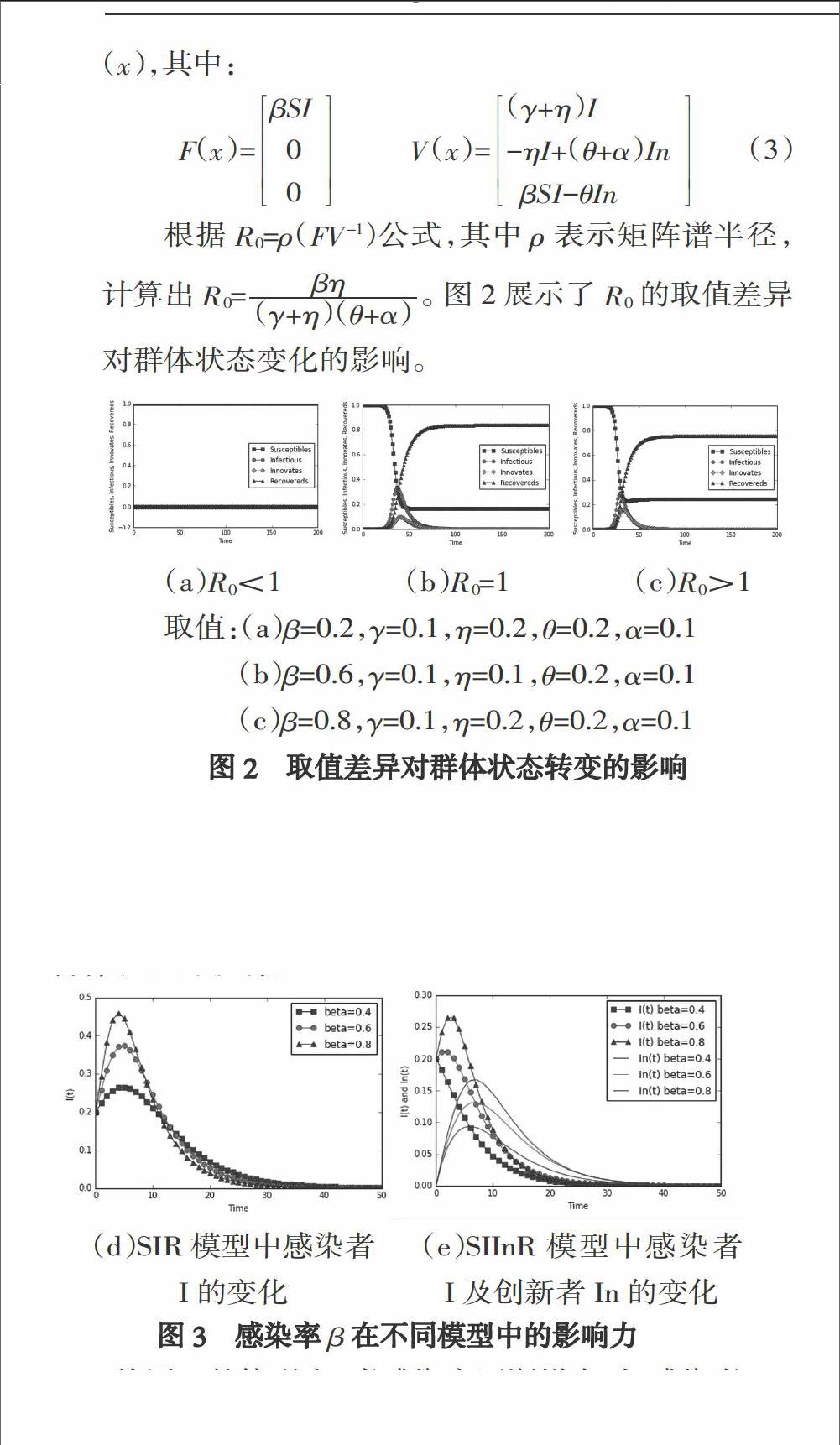
根據(jù)R0=ρ（FV-1）公式，其中ρ表示矩陣譜半徑，計算出R0=■。圖2展示了R0的取值差異對群體狀態(tài)變化的影響。

從圖2可以看出，當互聯(lián)網(wǎng)迷因刺激系統(tǒng)中的群體時， R0<1系統(tǒng)中的群體狀態(tài)不發(fā)生轉(zhuǎn)變，如（a）所示；R0=1群體狀態(tài)開始發(fā)生轉(zhuǎn)變，如（b）所示；R0>1系統(tǒng)中的群體狀態(tài)發(fā)生轉(zhuǎn)變，如（c）所示。

3 SIInR模型參數(shù)影響力分析

為了檢驗SIInR模型中5個參數(shù)的具體作用，本文采用python3.4.4編程，對比參數(shù)的取值差異對系統(tǒng)群體狀態(tài)的影響。

3.1 感染率β

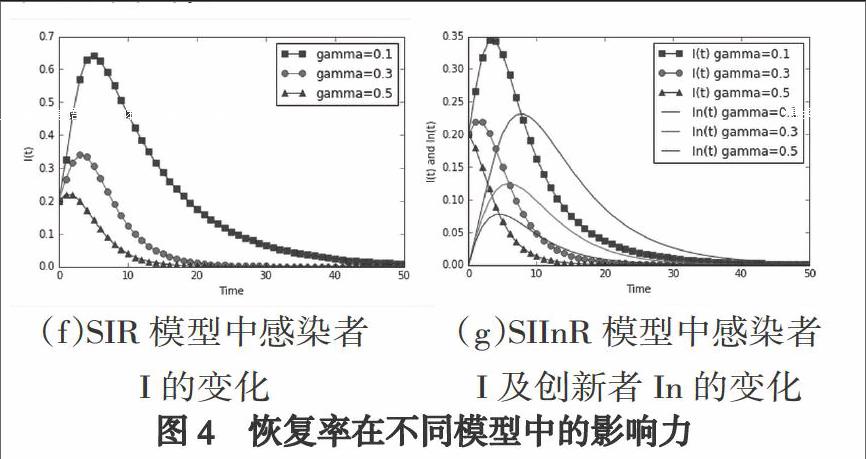
感染率β指在互聯(lián)網(wǎng)迷因的刺激下，易感者轉(zhuǎn)變?yōu)楦腥菊叩母怕剩敻腥韭试礁邥r，互聯(lián)網(wǎng)迷因的感染能力越強，易感者越快對互聯(lián)網(wǎng)迷因產(chǎn)生興趣。在SIR模型中，設置？酌=0.2；在SIInR模型中，設置？酌=0.2，？濁=0.2，？茲=0.1，？琢=0.1，圖3展示了感染率β分別為0.4、0.6、0.8時，傳統(tǒng)SIR模型及SIInR模型對系統(tǒng)群體狀態(tài)的影響。

從圖3整體觀察，當感染率逐漸增大時，感染者及創(chuàng)新者在兩個模型中的所占比例都逐漸增多，且均在交互50次時感染停止。具體對比（d）（e）兩個圖，當感染率β從0.4增加到0.8時，在SIR模型中，感染者的數(shù)量從0.25上升到0.45；在SIInR模型中，感染者的數(shù)量僅從0.2上升到0.255，創(chuàng)新者的數(shù)量從0.09上升到0.16，表明了在相同感染條件下，SIR模型的感染能力高于SIInR模型，原因是當系統(tǒng)感染發(fā)生時，互聯(lián)網(wǎng)迷因不僅使感染者產(chǎn)生興趣，還激發(fā)了創(chuàng)新者對互聯(lián)網(wǎng)迷因的創(chuàng)新意識，使感染者逐漸向創(chuàng)新者轉(zhuǎn)變，促進了個體對互聯(lián)網(wǎng)迷因的創(chuàng)新行為。

3.2 恢復率？酌

恢復率？酌指感染者轉(zhuǎn)變?yōu)槊庖哒叩母怕剩敾謴吐试礁邥r，感染者對互聯(lián)網(wǎng)迷因越快失去興趣。在SIR模型中，設置β=0.8；在SIInR模型中，設置β=0.8，？濁=0.2，？茲=0.2，？琢=0.2，圖4展示了恢復率？酌分別為0.1、0.3、0.5時，傳統(tǒng)SIR模型及SIInR模型對系統(tǒng)群體狀態(tài)的影響。

從圖4整體觀察，當恢復率？酌逐漸增大時，感染者及創(chuàng)新者在兩個模型系統(tǒng)中所占比例都逐漸減小，且均在交互50次時感染停止。具體對比（f）（g）兩個圖，當恢復率？酌從0.1變化為0.5時，在SIR模型中，感染者的數(shù)量從0.65下降到0.2；在SIInR模型中，感染者的數(shù)量從0.35下降到0.2，創(chuàng)新者的數(shù)量從0.23下降到0.07，說明了恢復率？酌能有效控制感染人數(shù)及創(chuàng)新人數(shù)的增長，因而，在互聯(lián)網(wǎng)迷因傳播過程中，減緩感染者或創(chuàng)新者失去興趣的速度能促進互聯(lián)網(wǎng)迷因持續(xù)性的發(fā)展。

3.3 創(chuàng)新率？濁

創(chuàng)新率？濁是感染者成為創(chuàng)新者的概率，當創(chuàng)新率越高時，原始互聯(lián)網(wǎng)迷因激發(fā)越多創(chuàng)新者的創(chuàng)新意識，使他們參與互聯(lián)網(wǎng)迷因的模仿、創(chuàng)新，創(chuàng)造出大量的新互聯(lián)網(wǎng)迷因。在SIInR模型中，設置β=0.8，？酌=0.2，？茲=0.1，？琢=0.1，圖5展示了創(chuàng)新率？濁分別為0.1、0.3、0.6時，SIInR模型對感染者I、創(chuàng)新者In群體狀態(tài)的影響。

從圖5中可以看出，當創(chuàng)新率？濁從0.1到0.6不斷增大時，創(chuàng)新者的數(shù)量從0.1上升到0.2，感染者的數(shù)量從0.35降低到0.2。當互聯(lián)網(wǎng)迷因刺激系統(tǒng)時，雖然創(chuàng)新者群體在不斷增多，但感染者群體卻逐漸減少，其原因是，當大量群體參與到互聯(lián)網(wǎng)迷因的模仿與創(chuàng)新時，可能改變了原始互聯(lián)網(wǎng)迷因的核心部分，使未接觸的群體不理解互聯(lián)網(wǎng)迷因表達的初始含義，從而對互聯(lián)網(wǎng)迷因不感興趣。因此，在創(chuàng)新過程中，創(chuàng)新者應多保留原始互聯(lián)網(wǎng)迷因的核心部分，小幅度的改造創(chuàng)新更有利于互聯(lián)網(wǎng)迷因的持續(xù)發(fā)展。

3.4 接觸率？茲

接觸率？茲指創(chuàng)新者將自己創(chuàng)新的互聯(lián)網(wǎng)迷因傳播給易感者的概率，當接觸率越高時，創(chuàng)新者具有越高的分享欲望。在SIInR模型中，將參數(shù)設置為β=0.8，？酌=0.1，？濁=0.4，？琢=0.1，圖6展示了接觸率？茲分別為0.1、0.3、0.5時，SIInR模型對易感者S、感染者I及創(chuàng)新者In群體狀態(tài)的影響。

觀察圖6中（h）（i）兩個圖，當接觸率？茲從0.1到0.5不斷增大時，感染者的最大數(shù)量均保持在0.2，但呈現(xiàn)出緩慢的下降趨勢；創(chuàng)新者的數(shù)量從0.25下降到0.13，呈現(xiàn)出逐漸減小的狀態(tài)；易感者的數(shù)量從0.37上升到0.5，呈現(xiàn)出逐漸增大的狀態(tài)，說明在新互聯(lián)網(wǎng)迷因的傳播過程中，接觸率？茲僅能有效影響易感者及創(chuàng)新者的數(shù)量變化，不直接影響感染者在系統(tǒng)中的所占比例，但會減緩感染者的下降趨勢，表明了新互聯(lián)網(wǎng)迷因的出現(xiàn)會降低群體對原始互聯(lián)網(wǎng)迷因的熱情，當新互聯(lián)迷因逐漸被易感群體接受時，原始互聯(lián)網(wǎng)迷因的感染者才開始呈現(xiàn)出緩慢下降的趨勢。

3.5 免疫率？琢

免疫率？琢指創(chuàng)新者逐漸對自己創(chuàng)新的互聯(lián)網(wǎng)迷因失去興趣，變成免疫者R的概率。在SIInR模型中，設置β=0.8，？酌=0.1，？濁=0.4，？茲=0.1，圖7展示了免疫率？琢分別為0.1、0.3、0.5時，SIInR模型對感染者I、創(chuàng)新者In及免疫者R群體狀態(tài)的影響。

觀察圖7中（j）（k）兩個圖，當免疫率？琢從0.1增加到0.5時，創(chuàng)新者的數(shù)量從0.25下降到0.1，免疫者的數(shù)量從0.5上升到0.7，而感染者的數(shù)量以及減緩趨勢基本無變化，說明了個體免疫能力越強，創(chuàng)新者對自己創(chuàng)造的新互聯(lián)網(wǎng)迷因越快失去興趣，免疫者群體的數(shù)量逐漸增大。當個體不傳播新互聯(lián)網(wǎng)迷因時，增強個體的免疫能力不影響原始互聯(lián)網(wǎng)迷因的趨勢發(fā)展。

4 實例仿真分析

根據(jù)互聯(lián)網(wǎng)迷因高速復制、快速滲透、傳播變異的特征，選取語句型互聯(lián)網(wǎng)迷因“友誼的小船”作為仿真對象，從百度指數(shù)中獲取2016年4月5日到2016年6月8日的日搜索趨勢，如圖8所示，圖中A-H點是個體創(chuàng)新行為引發(fā)多次病毒式傳播的集聚點，如將原始語句“友誼的小船說翻就翻”，創(chuàng)新為“愛情的巨輪說沉就沉”等。

圖8 百度指數(shù)中“友誼的小船”日搜索趨勢

從歷史趨勢中可以看出，網(wǎng)絡個體在64天中的日最高搜索量為14 000次。在SIInR模型中，設置β=0.5，？酌=0.01，？濁=0.1，？茲=0.01，當群體交互200次后，感染群體的仿真結(jié)果能較好擬合“友誼的小船”的日傳播趨勢，并可以推斷其他群體的發(fā)展趨勢。

根據(jù)圖9的傳播狀態(tài)，可計算出參與傳播的總?cè)丝跀?shù)約為25 000人，到目前為止大約還有5000個易感者未接觸到“友誼的小船”互聯(lián)網(wǎng)迷因，且2500個創(chuàng)新者的小幅度創(chuàng)新行為使互聯(lián)網(wǎng)迷因持續(xù)發(fā)展。仿真實驗說明了高感染率β、接觸率？茲，低恢復率？酌、創(chuàng)新率？濁、免疫率？琢能持續(xù)促進互聯(lián)網(wǎng)迷因的發(fā)展。

5 結(jié)語

在Web2.0的環(huán)境中，互聯(lián)網(wǎng)迷因的病毒式傳播發(fā)揮了巨大的社會影響力，日益受到國內(nèi)外多個領域研究者的關注。為了充分考量個體的創(chuàng)新行為對互聯(lián)網(wǎng)迷因的影響，本文在傳統(tǒng)SIR模型基礎上引入創(chuàng)新者人群（Innovative），構建SIInR互聯(lián)網(wǎng)迷因傳播模型，研究表明高感染率β、接觸率？茲，低恢復率？酌、創(chuàng)新率？濁、免疫率？琢能促進互聯(lián)網(wǎng)迷因的持續(xù)發(fā)展。本文構建的SIInR模型忽略了網(wǎng)絡環(huán)境對互聯(lián)網(wǎng)迷因的影響。在進一步研究中，將結(jié)合個體在社群中的結(jié)構位置，討論個體的創(chuàng)新行為對互聯(lián)網(wǎng)迷因在網(wǎng)絡環(huán)境中傳播發(fā)展的影響。

參考文獻：

[ 1 ] CHEN C C， CHANG C Y. Contents the creation and

meaning of internet memes in 4chan：popular internet culture in the age of online digital reproduction[J].Zoological Journal of the Linnean Society，2008，31（203）：14-30.

[ 2 ] SHIFMAN L. Memes in digital culture[M].Cambridge：The MIT Press，2014.

[ 3 ] DAVISON P. The language of internet memes[J].The

Social Media Reader，2012：120-134.

[ 4 ] CASTANO， D.， C. M. Defining and characterizing the

concept of Internet Meme[J].Ces Psicol，2013（6）：82-104.

[ 5 ] 何自然.語言中的模因[J].語言科學，2005，4（6）：54-64.

[ 6 ] 李捷，何自然.語言模因的主體性與語境化[J].外語學刊，2014（2）：59-64.

[ 7 ] 徐昊晟.基于模因論的語際語用課堂教學實驗研究[J].

外語教學，2015，36（3）：55-59.

[ 8 ] 張靖晨.中國媒體語言模因詞匯翻譯策略研究：以2007—2013年中國媒體新詞為例[D].哈爾濱：黑龍江大學，2014.

[ 9 ] 劉吉林，莫愛屏.網(wǎng)絡環(huán)境下學生語用能力培養(yǎng)的實證研究[J].當代外語研究，2014（10）.

[10] BAUCKHAGE C. Insights into Internet memes[C].In-

ternational Conference on Weblogs & Social Media， 2011.

[11] BAUCKHAGE C， KERSTING K， HADIJI F. Mathem-

atical models of fads explain the temporal dynamics of internet memes[C]//International Conference on Weblogs & Social Media，2013.

[12] PREOCTIUC-PIETRO D， COHN T. A temporal model of text periodicities using gaussian processes[C]//Conference on Empirical Methods in Natural Language Processing，2013.

[13] SEGEV E， NISSENBAUM A， STOLERO N， et al.

Families and networks of internet memes：the relationship between cohesiveness， uniqueness， and qui-

ddity concreteness[J].Journal of Computer-Mediated

Communication，2015，20（4）：417-433.

[14] SHAMMA D A， KENNEDY L， CHURCHILL E F. Peaks and persistence：modeling the shape of microblog conversations[C]//Hangzhou：ACM Conference on Computer Supported Cooperative Work，CSCW，2011.

[15] KAMATH K Y， CAVERLEE J， LEE K，et al. Spatio-temporal dynamics of online memes：a study of geo-tagged tweets[C]//International Conference on World Wide Web.International World Wide Web Conferences Steering Committee，2013.

[16] KOTSAKOS D， SAKKOS P， KATAKIS I， et al. Lan-

guage agnostic meme-filtering for hashtag-based social network analysis[J].Social Network Analysis and Mining，2015，5（1）：1-14.

[17] COSCIA M. Competition and Success in the Meme Pool：a Case Study on Quickmeme.com[EB/OL].[2016-02-20].http：//xueshu.baidu.com/s？wd=paperuri%3A%2881dd

616f237774d55c9e79437448690.f%29&filter=sc_long

_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http

%3A%2F%2Fwww.arxiv.org%2Fabs%2F1304.1712%3Fcontext%3Dcs.SI&ie=utf-8&sc_us=5919594280267

186174.

[18] COSCIA M. Average is boring： how similarity kills a meme's success[J].Scientific Reports，2014（4）：6477-6477.

[19] WENG L， FLAMMINI A， VESPIGNANI A， et al. Com-

petition among memes in a world with limited attention[J].Scientific Reports，2012，2（7391）：1-8.

[20] BRODIE R. Virus of the mind：the new science of the meme[M].Seattle，Wash.：Integral Press，1996.

[21] WANG L， WOOD B C. An epidemiological approach to model the viral propagation of memes[J].Applied Mathematical Modelling，2011，3（11）：5442-5447.

[22] TOWERS S， PERSON A， CASTILLO-CHAVEZ C. Modeling social media memes as a contagious process[EB/OL].[2016-02-20].http：//www.sherrytowers.com/latex_example.pdf.

[23] FREITAG D， CHOW E， KALMAR P， et al. A corpus of online discussions for research into linguistic memes[C]//Web as Corpus Workshop（WAC7），2012.

[24] BAUCKHAGE C， HADIJI F， KERSTING K. How viral are viral videos？[EB/OL].[2016-02-20].http：//www.aaai.org/ocs/index.php/ICWSM/ICWSM15/paper/download/10505/10485.

[25] WENG L， MENCZER F， AHN Y Y. Virality prediction and community structure in social networks[J].Scientific Reports，2012，3（8）：618-618.

[26] WEI X， VALLER N， PRAKASH B A， et al. Competing memes propagation on networks：a case study of composite networks[J].Acm Sigcomm Computer Communi-

cation Review，2012，42（5）：5-12.

[27] WEI X， VALLER N C， PRAKASH B A， et al. Competing memes propagation on networks：A network science perspective[J].Selected Areas in Communications，IEEE Journal on，2013，31（6）：1049-1060.

[28] ZHAO L， WANG J， CHEN Y， et al. SIHR rumor spreading model in social networks[J].Physica A：Statistical Mechanics and its Applications，2012，391（7）：2444-2453.

[29] ROCHA A F D， MASSAD E， SANTOS P C C D， et al.

A neurobiologically inspired model of social cognition：memes spreading in the Internet[J].Biologically Inspired

Cognitive Architectures，2015（14）：86-96.

[30] DIEKMANN O， HEESTERBEEK J A P， METZ J A J. On the definition and the computation of the basic reproduction ratio R， 0， in models for infectious diseases in heterogeneous populations[J].Journal of Math-

ematical Biology，1990，28（4）：365-382.

[31] VAN DEN DRIESSCHE P， WATMOUGH J.Reprod-

uction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission[J].Mathematical biosciences，2002，180（1）：29-48.

[32] HETHCOTE H W. The mathematics of infectious dis-

eases[J].SIAM Review，2000，42（4）：599-653.

[33] 廖曉昕.動力系統(tǒng)的穩(wěn)定性理論和應用[M].北京：國防工業(yè)出版社，2000.

張 頔 天津科技大學經(jīng)濟與管理學院碩士研究生。天津，300222。

（收稿日期：2016-07-18 編校：陳安琪）