不確定因素下基于多供應主體的應急物資供應模型*
王 茵,胡大偉
(長安大學 汽車學院,陜西 西安 710064)
0 引言
與傳統的商業物流不同,應急物流具有突發性、不確定性、弱經濟性和非常規性[1-2]的特點。為保證救災快速有效開展,我國政府考慮地域特點和人口分布,在全國設立了多個中央物資及地方儲備庫以應對未來可能發生的災害,這些儲備庫在近年災害發生時發揮了重要作用,但同時也顯現出儲備種類和數量較少、供應柔性差[3]和庫房管理問題多等不足。因此,儲備庫不能完全滿足應急物資供應需求,由經過政府認證的協議供應商參與是非常必要的[4]。協議供應商模式是國家及各級政府在儲備庫之外,為保證應急物資持續供應能力,與相關企業簽訂協議,由企業提供應急物資存儲管理和災害時期物資生產能力,以保證應急物資供應的方式。根據救災物資的特點[5],協議供應商可分為:制造型供應商,指能在災害發生后生產加工并持續供應補充救災物資的制造企業,體積大、儲備量小、對自然災害專用性強的物資,如救生設備、帳篷、移動廁所、發電機等需要這類協議制造商;儲備型供應商,指具有較強儲備能力,有多個儲備地且地域覆蓋面廣,可在短期內從多地提供大量多種物資的供應商,如大型超市或庫存批量大的企業,食品等通用物資需要這類協議供應商。協議供應商由政府災前完成認證選擇,根據當地預測需求,政府選擇儲備供應商增加關鍵物資的儲備量,選擇制造供應商在災后提供持續供應。
實際救災過程中,除政府統一安排的物資救助外,社會各界也會自發進行物資捐贈,這些捐贈物資品類復雜,數量和時間不可預測,通常先存入配送中心,再根據需要運至災區。配送中心因而出現不定期爆倉現象,導致運作管理能力下降,進而面臨物資滯后配送的風險,如果臨時增加配送中心點,則選址、經濟成本、時間成本、管理、協調控制等方面均存在難度和不可控因素。因此,需考慮從物資供應方的角度克服爆倉導致的供應能力下降問題。自然災害破壞下,災區道路通常有不同程度的損壞,影響物資運輸進度,若在救災初期不限制供應數量,將很快造成災區道路擁堵,使物資供應渠道縮小,物資供應難度進一步增加。為此,加入以上2種不確定因素作為供應模型限制條件進行討論。
當前基于協議供應商參與的應急物資管理方面的研究主要集中于供應商選擇[6]、采購策略[7]和儲備策略研究[8]等,對多供應主體下物資供應的問題研究較少。Balcik和AK[9]構建在救援組織同供應商簽訂應急救援物資儲備框架協議前提下的物資供應動態規劃模型,按照模型規劃的方案,供應商在災害發生后將協議數量的應急物資直接送至受災區域;王茵等[10]提出在物資接收能力正常的環境下,基于多供應主體模式的物資供應模型,通過與實際地震案例數據對比,分析該供應模式對提升供應效率和穩定性的作用。但以上文獻均未考慮不確定因素的影響。在應急救援物資供應和分配的研究中,對不確定因素的考慮集中在自然環境的不確定和災區信息的不確定,如Zhang等[11]提出考慮次生災害影響的多物資多倉庫的混合整數模型,并運用啟發式搜索法求解,實現最少延遲;Sheu[12]提出在災區信息不完整情況下,通過數據融合修正需求信息,以模糊聚類法將災區分組后再進行物資配送,并實驗證明該方法可有效減少物資分配誤差;Chakravarty[13]研究在災難強度和實際損害等不確定條件下的人道救援供應鏈快速響應問題,并提出2階段的供應決策模型;Chang等[14]提出能夠調節可用資源的調配并自動生成多樣有效的應急物流計劃的多目標模型,運用基于貪婪搜索的遺傳算法,并以臺灣某地震為例,仿真證明該算法的優勢。這些文獻從多個角度改進應急物資分配方案,使其更貼近實際情況,應用范圍更廣,但都未考慮供應設施的能力限制對救援的影響。對于災區道路破壞環境下調度問題,Duque等[15]提出自然災害破壞道路時,應急維修工程團隊的調度和路由問題,以最小時間通路為目標建立決策模型,并開發動態規劃算法和迭代的隨機貪婪算法來解決該問題,但未涉及同情況下的物資調度;葉永等[16]提出“觀測-決策-配置”的3階段決策方法,以隨機變量的形式記錄道路損毀率的歷史信息和樣本信息,應用貝葉斯分析等對基于道路損壞率信息更新的應急資源配置決策問題進行建模,并設計遺傳算法求解,通過數值仿真驗證模型和算法的有效性;陶玉旻[17]建立考慮突發自然災害道路損壞率和維修周期的,以供應量總損失最小為目標的調度模型,利用Matlab和Lingo求解,并結合實例對模型進行求解和有效性驗證。但以上研究均為單種物資供應方案,不能完全應用于實際救災環境。
綜上所述,目前學者們對于實際救災中供應設施和道路能力缺陷壞境下的物資供應問題研究較少。因此,以協議供應商參與的多主體供應為模式,構建供應設施和環境不確定條件下的雙層應急物資供應模型,以NSGAⅡ法和CPLEX求解供應方案,分析和驗證該模式在不確定環境下對保證物資供應的作用和較傳統物資庫供應模式的優勢。
1 不確定因素下基于多供應主體的應急物資供應模型
1.1 問題描述
大規模自然災害發生后,道路遭受一定程度破壞,需要根據物資需求和道路實際通行能力分配物資在每條路通行量,在物資供應的T個周期中,道路通行能力可能因搶修或次生災害而改變,故需在每個周期初進行更新,分配到每條路的通行量也隨之更新。為便于應急疏散的逆向車道設置[18],道路通行能力滿足物資需求時,應保證道路占用量最小。物資供應方分別由配送中心、中央儲備庫及已認證的協議供應商組成,接收方由配送中心和災區組成,如圖1所示。由于配送中心向災區供應物資較供應商直送更好管理和控制,故配送中心為災區的主供應方,即當配送中心未爆倉時,決策者選擇合適的供應主體,將應急物資發運至配送中心,再由配送中心按照實際接收量發運至災區區域。當配送中心爆倉時,為減小配送中心庫存壓力,所有供應方直送物資到災區。該模型相比以往應急物資供應模型,結合實際,考慮災區的道路能力限制和配送中心可能爆倉的不確定因素,并解決此情形下產生的配送中心供應能力下降及災區道路擁堵導致物資無法送達的問題,證明加入2種職能的協議供應商對緩解配送中心爆倉和增強物資供應調配柔性起到關鍵作用。

圖1 多主體物資供應方式Fig.1 Diagram of multi supply subjects supplying
為便于模型建立,作如下假設:
1)由于每個災區區域覆蓋多個受災點,為便于調配管理,1個配送中心只對應負責1個災區區域的物資供應。
2)每種物資的供應商已選定,中央儲備庫和儲備型供應商可存儲多種物資,可供應多個配送中心,因單周期內產量有限,每個制造型供應商在1個周期內只為1個配送中心供貨。
3)不能在周期時長內運到的在途物資,累積到下1周期接收數量中,配送中心發出的物資可在當周期到達災區。
4)多個災區之間道路不重合。
5)運輸車輛規格相同。
1.2 模型構建
1.2.1符號說明

表1 符號說明
1.2.2數學模型
1)上層優化模型:
(1)
(2)
約束條件:
fzl(t)≤Czl(t),?(z∈Z)
(3)
fzl(t)=Czl(t),
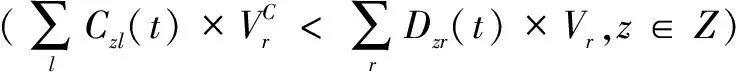
(4)
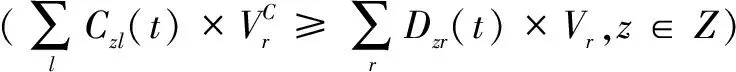
(5)
fzl(t)≤ezl(t)×M,?(z∈Z)
(6)
ezl(t)≤fzl(t)×M,?(z∈Z)
(7)
ezl(t)∈{0,1},?(z∈Z)
(8)
fzl(t)≥0,?(z∈Z)
(9)
說明:式(1)表示最小化道路數;式(2)表示最小化配送中心通過道路至災區的總距離;式(3)表示分配的道路通行量應不大于道路通行能力;式(4)表示若道路通行能力總和小于對應災區需求量,那么分配的通行量即為道路通行能力;式(5)表示若道路通行能力總和大于對應災區需求量,那么分配的通行量應不小于需求量;式(6)和式(7)表示若道路被選中就分配通行量,若不被選中就不會分配通行量;式(8)為0-1變量;式(9)為非負約束。
2)下層優化模型:
(10)
約束條件:

(11)
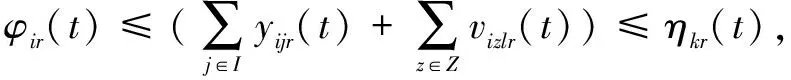
(12)
xijr(t)+wizlr(t)≤1,?(j∈I,z∈Z)
(13)
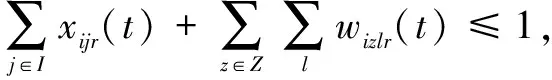
(14)
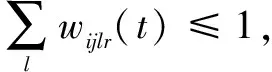
(15)
ukjlr(t)=vkjlr(t),?(k∈I,j∈Z)
(16)
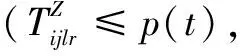
(17)
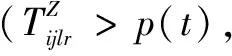
(18)
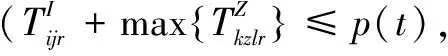
i∈K∪S∪P,z∈Z,k∈I,j∈I)
(19)
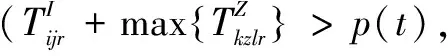
(20)
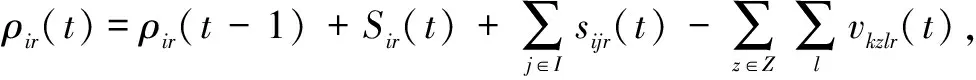
(21)
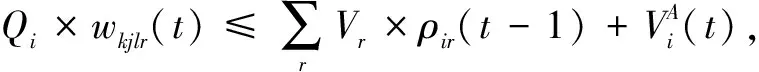
(22)
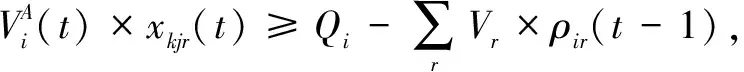
(23)
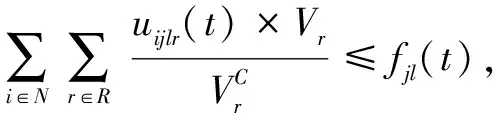
(24)
yijr(t)≤xijr(t)×M
(25)
xijr(t)≤yijr(t)×M
(26)
vijlr(t)≤wijlr(t)×M
(27)
vijlr(t)≤wijlr(t)×M
(28)
xijr(t)∈{0,1},wijlr(t)∈{0,1}
(29)
yijr(t),sijr(t),vijlr(t),uijlr(t),ρir(t)≥0
(30)
說明:式(10)表示最小化接收方偏差影響度;式(11)表示中央儲備庫或儲備型供應商總發貨量小于其庫存量;式(12)表示協議供應商物資配送量小于等于生產能力,且大于等于最小發貨量;式(13)表示供應方在1個周期內只為1種接收方供貨,即不得同時發貨至配送中心和災區;式(14)表示在周期t內1個制造型供應商只為1個接收方供貨;式(15)表示在周期t內,供應商只選1條路供應物資到災區;式(16)表示配送中心向災區供應的物資可在周期內到達災區;式(17)和式(18)表示若物資由供應方供應到災區的時間在周期內,則災區收貨量即為供應量,若物資由供應方供應到災區的時間超出周期時長,則物資在下1個周期到達災區;式(19)和式(20)表示若物資由供應方供應到配送中心的時間在周期內,則配送中心收貨量即為供應量,若物資由供應方供應到配送中心的時間超出周期時長,則物資在下1個周期到達災區;式(21)表示配送中心i在周期t結束時物資r剩余庫存量計算式;式(22)表示若配送中心未爆倉,其他供應方不得直送物資到災區;式(23)表示若配送中心爆倉,其他供應方不得供應物資到配送中心;式(24)表示周期t內每條道路物資總接收量不超過道路通行量;式(25)和式(26)表示供應方被選中向配送中心供貨就一定有供應量,未被選中就沒有供應量;式(27)和式(28)表示供應方被選中向災區供貨就一定有供應量,未被選中就沒有供應量;式(29)為0-1決策變量;式(30)為非負約束。
1.2.3參數求解說明
參數中,Czl(t)為通往災區z的第l條路在周期t的通行能力,由于地震災害會破壞道路物理結構,對物資運輸產生持續性影響,同時余震、泥石流等次生災害可能在救災過程中再次影響道路通行能力,故道路通行能力應在每個周期都進行評估。災害影響下通行能力折算公式,根據文獻[19]按模型場景改進如下:
(31)
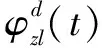
2 模型求解
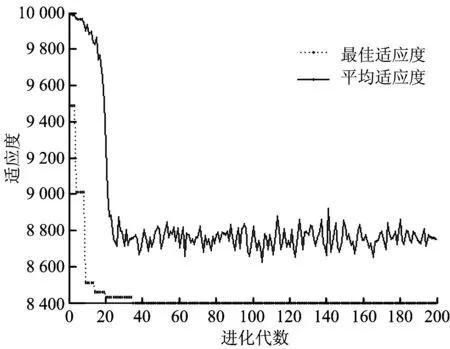
雙層模型中,上層模型為雙目標模型,選擇用帶精英策略的非支配集排序遺傳算法(NSGAⅡ)求解。
2.1 算法具體步驟
算法采用實數編碼,設N為種群規模,T和t分別是最大進化代數和當前進化代數。
1)初始化種群,令t=0。
2)生成滿足約束條件的個體n個,計算個體的目標函數值,對個體進行非支配排序,并生成父代種群。
3)采用錦標賽選擇,算術交叉、非均勻變異對父代種群進行遺傳操作,生成新種群。
4)對新種群中不滿足約束的個體,由產生的滿足約束個體替換,生成子代種群,以2個目標值為適應度函數計算父、子代種群個體適應度。
5)父、子代種群合并,進行非支配排序,排名前N的作為新種群。
6)若t 快速非支配排序:設種群P中每個個體p都有2個參數np和Sp,np為種群中支配個體p的解個體的數量,Sp為被個體p所支配的解個體的集合。初始化設i=1,prank=i。 1)令集合Fi=φ,找出種群P中所有np=0的個體,將它們存入集合Fi。 2)令Q=φ,考察Fi中每個個體q所支配的個體集Sq,執行nq=nq-1,若nq=0,則將個體存入Q。 3)令i=i+1,prank=i,Fi=Q,若Fi≠φ,轉入2);否則算法結束。 最終,所有個體均被分層并賦予排序號。 擁擠距離是指在種群中給定個體周圍個體的密度,即種群中個體所處環境的擁擠程度,與目標函數值有關,用id表示,計算方法:確定集合I中解個體的個數l,對于每個Fi中的個體,在目標函數m下對個體進行非支配排序,即I=sort(Fi,m)。令邊界個體的擁擠距離為無限大,即I[1]d=I[l]d=∞,對于第2到l-1個體利用式(32)進行計算。 (32) 其中,I[i]m表示集合I中第i個個體對于第m個目標函數的值。經過排序和擁擠度計算,可確定任意2個個體支配和非支配關系,即當滿足prank 某地區發生地震災害后,救災部門根據災情將災區分為2個,對應2個配送中心均在該地震省份的省會城市,距供應方或災區距離均相同,每個災區對應3條道路,救災周期為4個,每個周期時長為24 h,應急物資為帳篷(R1)、棉被(R2)、食品(R3)、飲用水(R4),體積分別為0.2 m3/件、0.15 m3/件、1m3/t和3.22 m3/t,裝車體積均為10 m3/車。配送中心2在全周期內未接收這4種物資捐贈,2個配送中心的設計容量分別是5 000 m3和4 000 m3,它們到對應災區時間最大值均為8.5 h,2個災區各周期物資緊急度權重一致,當t=1,2,3時,為(0.6,0.2,0.1,0.1);當t=4時,為(0.3,0.5,0.1,0.1)。其他數據見表2~表6。 表2 災區需求量數據 表3 災區道路情況數據 表4 中央物資庫基本情況數據 表5 供應商能力數據和到配送中心距離數據 表6 配送中心收到的捐贈物資情況 分別采用NSGAⅡ算法在matlab求解上層模型,CPLEX求解器編程求解下層模型,在Intel core i5 @ 1.80 GHz CPU,4.00 G內存的電腦上運行。NSGAⅡ算法參數為:種群規模100,最大迭代次數200次,交叉概率0.8,變異概率0.2。CPLEX計算中,約束20 336個,變量3 425個,非零系數61 848個,迭代3 169次。 3.2.1上層模型求解結果 在本案例中,由于周期t=1時,2個災區的物資需求均大于道路總容量,通行量即為道路容量,故染色體為18個。在Matlab運行結果如圖2和圖3所示,總道路占用量最低為19條,對應累積距離和最少為8 430 km。這里列出累積行駛距離最小的1組Pareto最優解,按照優先大容量道路的原則對通行能力進行分配,作為下層模型的已知變量,如表7所示。 圖2 目標函數1運算變化Fig.2 Operation result of OBJ1 圖3 目標函數2運算變化Fig.3 Operation result of OBJ2 周期Z1L1L2L3Z2L4L5L6t=11179835734228t=211716235100710t=3200073100064t=4200069100620 3.2.2下層模型求解結果 下層目標函數值為2 019.6,因篇幅有限,僅將周期1和周期2的應急物資調配方案列出,見圖4和圖5。周期t=1時,配送中心均未爆倉,救災物資均運輸至配送中心再統一送往災區。各供應方向2個配送中心供應4種物資的總發貨量分別為[4 799,25 183,44,0]、[3 623,15 183,0,0],其中在途物資分別為[1 804,8 075,0,0],由于物資需求量大,災區道路通行能力差,應急物資無法全部送達目的地,物資R3和R4緊急度級別偏低,未安排發貨,災區1和災區2分別有[0,1 744,33,103]和[0,1 513,20,62]的缺貨量。周期t=2時,配送中心1由于接收捐贈物資過多爆倉,只接收t=1在途的物資,其他物資均由其他供應方直送,各供應方向災區1供應的總發貨量為[5 920,18 172,44,55],其中物資R1和R2分別有2 912件和4 714件在途,向配送中心2供應的總發貨量是[394,7 441,27,33],其中物資R1和R2均為在途物資,配送中心2按需求量供應至災區。由于道路通行能力提升,該周期內調配的物資滿足災區需求。 圖4 周期t=1物資供應方案Fig.4 Resource supplying plan in period 1 圖5 周期t=2物資供應方案Fig.5 Resource supplying plan in period 2 由物資供應方案可以看出,雖然中央儲備庫缺少R3和R4這2種物資,但通過及時調度協議供應商的物資資源,這2種物資并未因庫存不足而缺貨。當配送中心爆倉時,協議供應商在政府協調下直送物資至災區,既保證物資及時到達災區,又緩解配送中心庫存處理壓力,如圖5所示。當災區道路因損壞通行能力下降時,協議供應商在政府協調下暫緩供應優先級較低的物資,如圖4所示,使災區在供應影響最小情況下降低災區道路擁堵,為道路維修和物資順利到達創造條件。 (33) 即,當行駛車輛數超過安全車速下通行能力時,道路通行能力會隨車輛數增加而下降;當行駛車輛數超過最大行車能力時,交通完全癱瘓,無法通行;配送中心爆倉時發貨效率按照上述公式同理獲得。 以t=1時災區1為例,設道路影響系數為0.8,配送中心運作影響系數為0.7,通往災區1的3條路的最大行車能力分別是230,300,120,配送中心1最大庫存能力是5 500 m3,在政府采購的非儲備物資可在t=1周期內到達的理想狀態下,根據式(33)和CPLEX計算協議供應商參與的多主體在不確定條件下供應能力對比如表8和表9所示。 表8 多供應主體直送效果對比 表9 多供應主體控制供應效果對比 基于以上數據計算結果,協議供應商參與的多主體供應模式,相比單一儲備庫供應模式而言,優勢如下: 1)配送中心爆倉時,供應商自主配送起到積極作用,從表8可以看出,即使配送中心已完全無法接收物資,也可通過協議供應商直送滿足災區需求。若沒有協議供應商,政府采購的非儲備庫可供應物資,因一次采購數量大、到貨時間不確定且都需要在配送中心中轉等原因,將造成配送中心長時間爆倉,發貨能力下降。 2)災區道路損壞或擁堵時,各供應方可按物資需求優先級進行緩送,協議供應商因其在平時就與政府相關部門建立信息聯系,可快速響應緩送要求,及時調整向配送中心和災區供應物資的方案,配合政府統一安排物資調度,對緩解災區道路通行壓力起到積極作用。 1)提出由政府認證的協議供應商參與的多主體應急物資供應模式。 2)在分析配送中心爆倉和災區道路損壞等影響物資供應的不確定因素基礎上,建立基于多供應主體的應急物資供應雙層優化模型,以解決多主體下物資供應問題。 3)分別采用NAGSⅡ算法和CPLEX求解器對模型進行求解,通過算例分析和供應效果對比,驗證多主體供應模式通過物資直送和緩送的方式可有效緩解不確定因素帶來的供應能力降低的壓力,使需求得到最大限度滿足。 [1]Sheu J B. Challenges of emergency logistics management[J]. Transportation Research Part E Logistics & Transportation Review, 2007, 43(6):655-659. [2]Zuo X, Ran Q, Gu W. Research on Situations and Development Trends of Emergency Logistics at Home and Abroad[M]// Advances in Grey Systems Research. Springer Berlin Heidelberg, 2010:581-587. [3]高建國, 賈燕, 李保俊,等. 國家救災物資儲備體系的歷史和現狀[J]. 國際地震動態, 2005(4):5-12. GAO Jianguo,JIA Yan,LI Baojun,et al. The historical and present situation of the state reserve system of rescue goods and materials[J]. Recent Developments in World Seismology,2005(4):5-12. [4]沈星辰, 樊博. 信息共享、應急協同與多源物資儲備的關系研究[J]. 科技管理研究, 2015,35(15):216-221,239. SHEN Xingchen, FAN Bo. Information sharing, collaborative response and relief supplies in emergency preparation[J]. Science and Technology Management Research,2015,35(15):216-221,239. [5]張文峰. 應急物資儲備模式及其儲備量研究[D]. 北京:北京交通大學, 2010. [6]劉乃娟. 應急物資采購的供應商選擇研究[D]. 北京:北京交通大學, 2011. [7]田軍, 葛永玲, 侯叢叢. 政府主導的基于實物期權契約的應急物資采購模型[J]. 系統工程理論與實踐, 2014, 34(10):2582-2590. TIAN Jun, GE Yongling, HOU Congcong.Government-driving emergency supplies procurement model based on real option contract[J]. Systems Engineering-Theory&Practice, 2014, 34(10):2582-2590. [8]李明. 政企聯合情景下應急救援物資儲備研究[D]. 濟南:山東大學, 2016. [9]Balcik B, Ak D. Supplier selection for framework agreements in humanitarian relief[J]. Production & Operations Management, 2013, 23(6):1028-1041. [10]王茵, 胡大偉, 李博. 基于多供應主體的應急物資供應模型[J]. 長安大學學報:自然科學版, 2016,36(6):98-104. WANG Yin,HU Dawei,LI Bo.Emergency resource relief model under multi-supply subjects[J].Journal of chang’an university:natural science edition,2016,36(6):98-104. [11]Zhang J H, Li J, Liu Z P. Multiple-resource and multiple-depot emergency response problem considering secondary disasters[J]. Expert Systems with Applications, 2012, 39(12):11066-11071. [12]Sheu J B. Dynamic relief-demand management for emergency logistics operations under large-scale disasters[J]. Transportation Research Part E Logistics & Transportation Review, 2010, 46(1):1-17. [13]Chakravarty A K. Humanitarian relief chain: Rapid response under uncertainty[J]. International Journal of Production Economics, 2014, 151:146-157. [14]Chang F S, Wu J S, Lee C N, et al. Greedy-search-based multi-objective genetic algorithm for emergency logistics scheduling[J]. Expert Systems with Applications, 2014, 41(6):2947-2956. [15]Duque P A M, Dolinskaya I S, S?rensen K. Network repair crew scheduling and routing for emergency relief distribution problem[J]. European Journal of Operational Research, 2016, 248(1):272-285. [16]葉永, 劉南, 詹沙磊. 基于信息更新的應急資源配置序貫決策方法[J]. 浙江大學學報工學版, 2013, 47(12):2212-2220,2242. YE Yong,LIU Nan,ZHAN Shalei. Informationupdate based sequential approach for emergency resources allocation planning[J]. Journal of Zhejiang University (Engineering Science),2013,47(12):2212-2220,2242. [17]陶玉旻. 突發自然災害下的應急物資調度研究[D]. 武漢:武漢理工大學, 2014. [18]脫俗. 應急疏散條件下的逆向車道設置研究[D]. 蘭州:蘭州交通大學, 2015. [19]牛世峰. 災害條件下路網交通運行態勢快速分析與評估技術研究[D]. 長春:吉林大學, 2011. [20]陳靜鋒. 震后道路保障能力與應急物資配送的優化研究[D]. 大連:東北財經大學, 2014.2.2 算法操作說明
3 案例分析
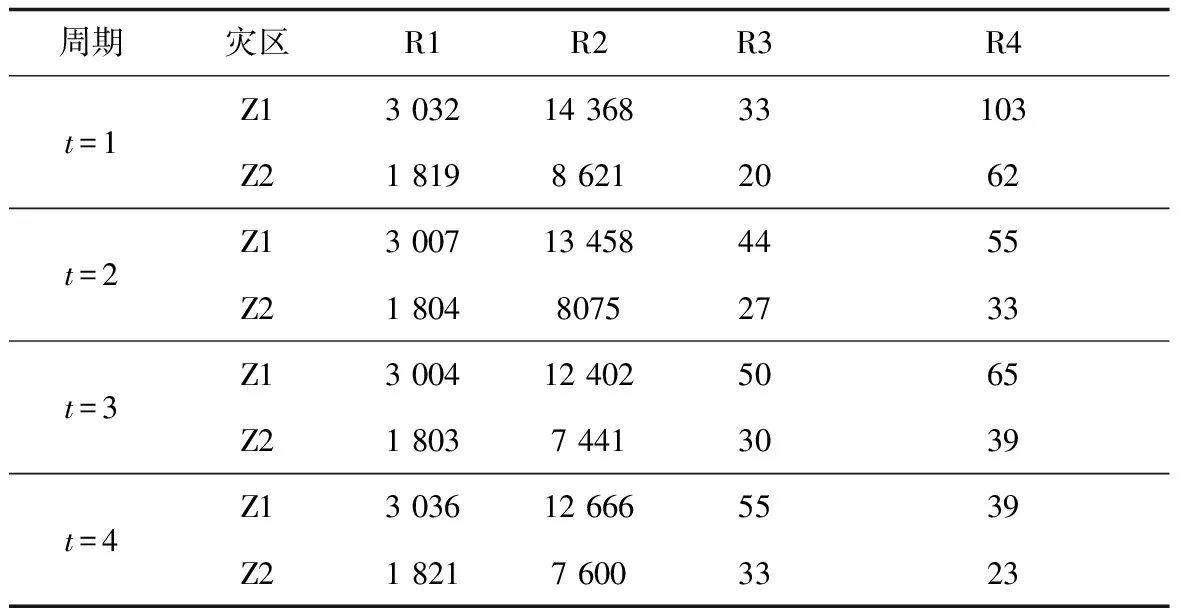
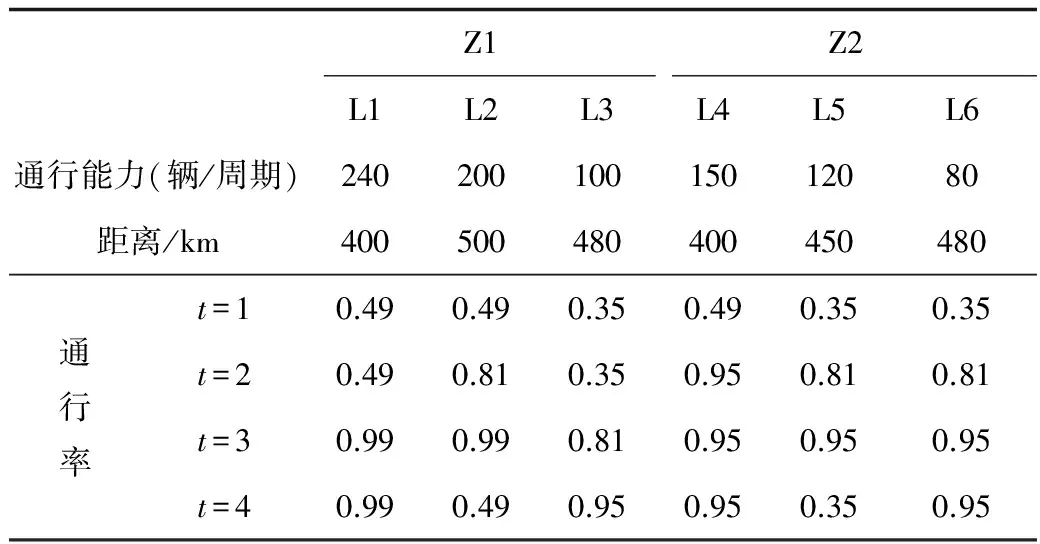
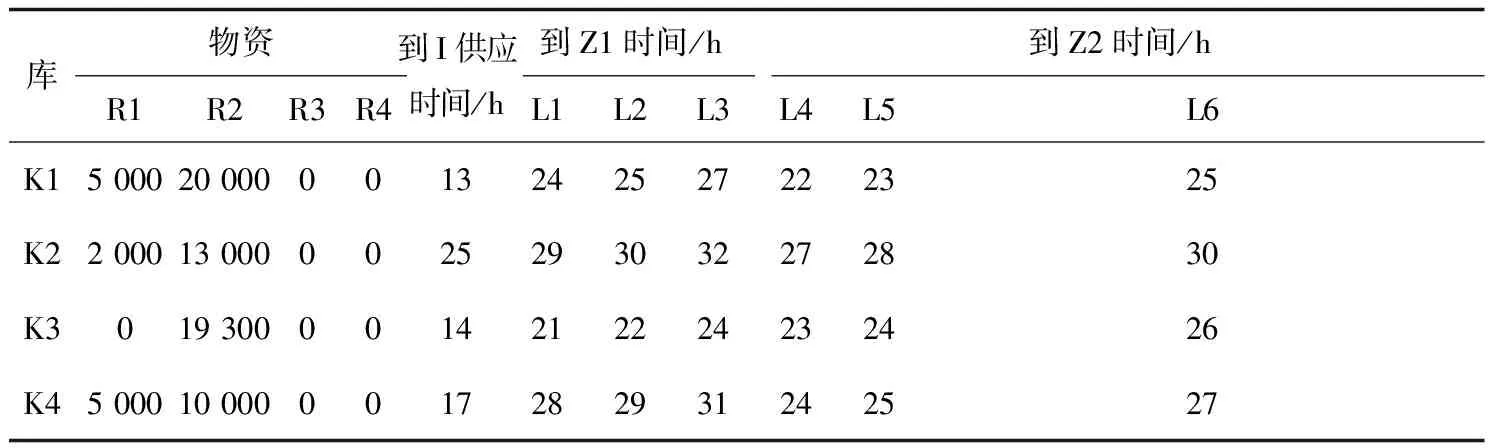
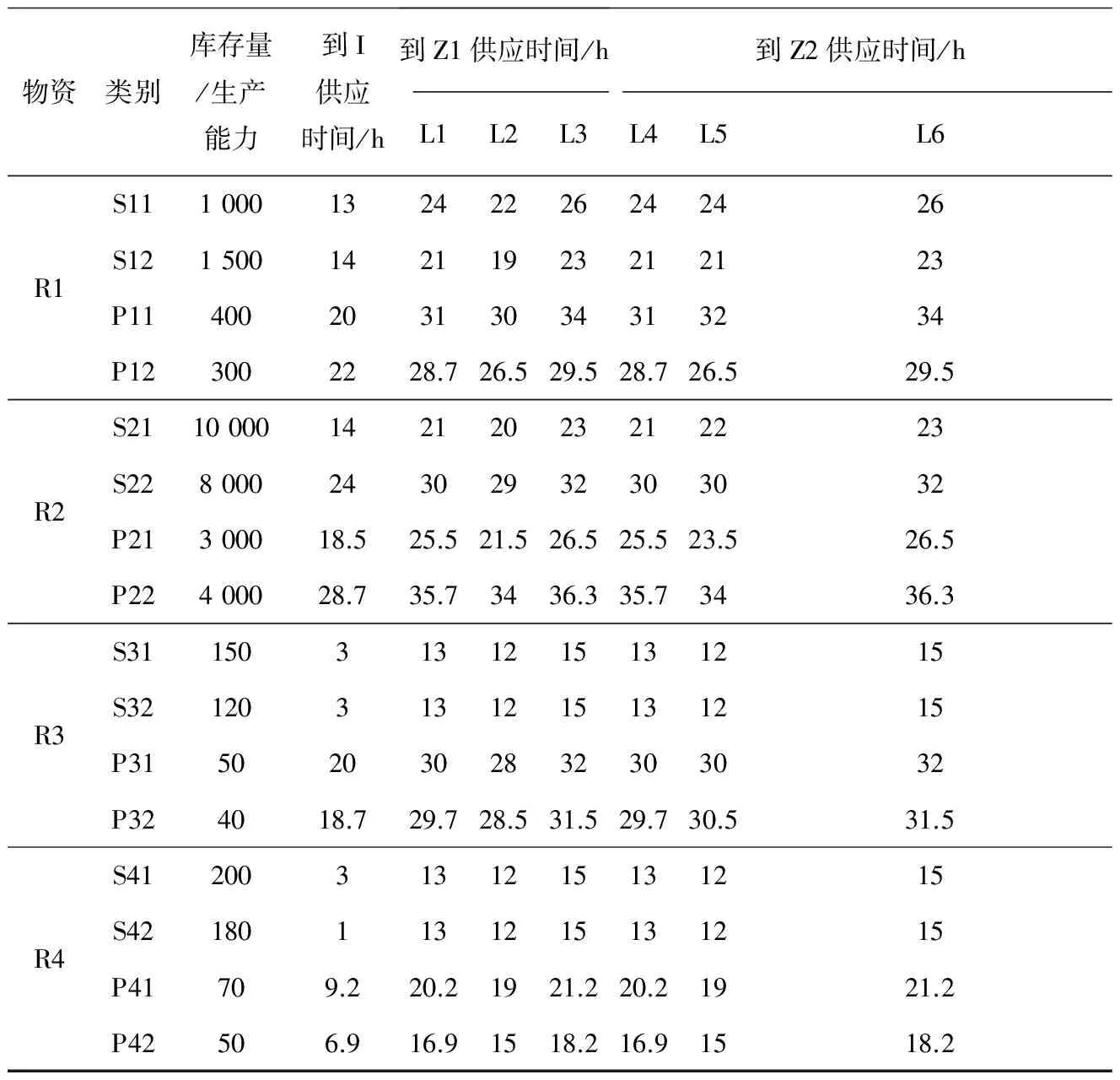
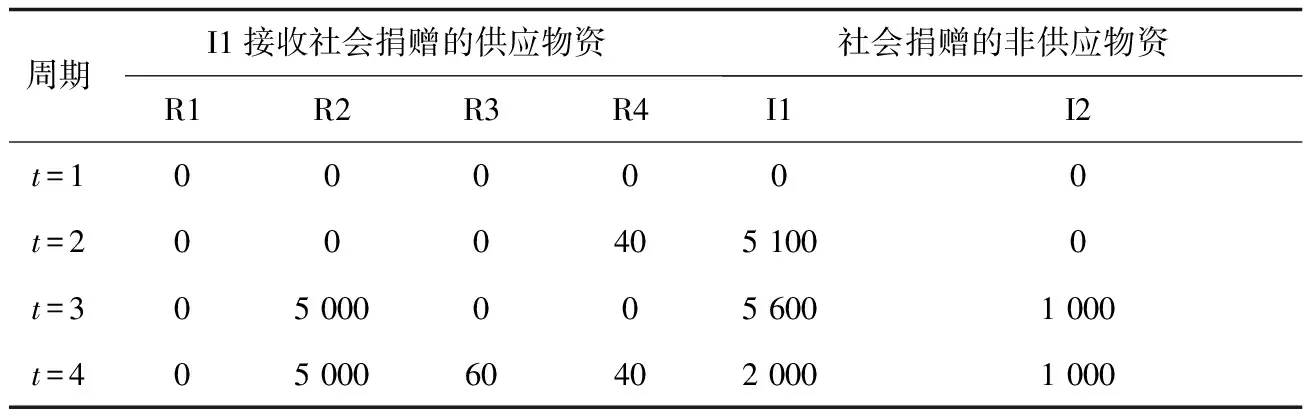
3.1 案例說明
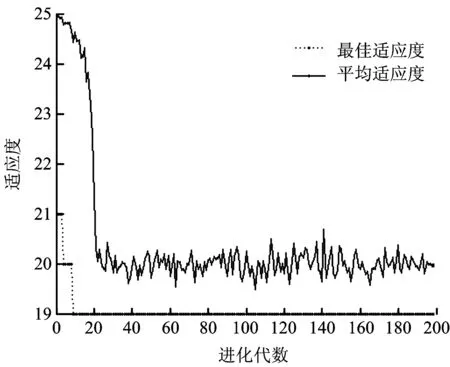
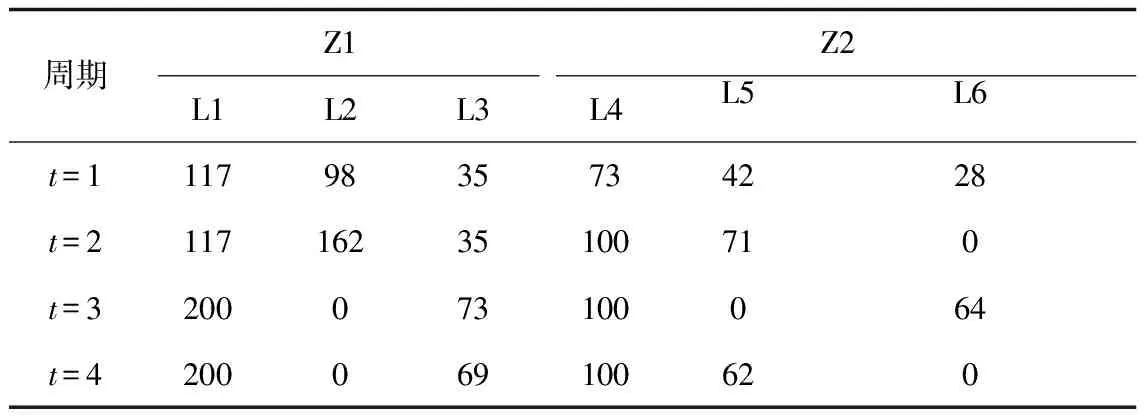
3.2 供應方案求解
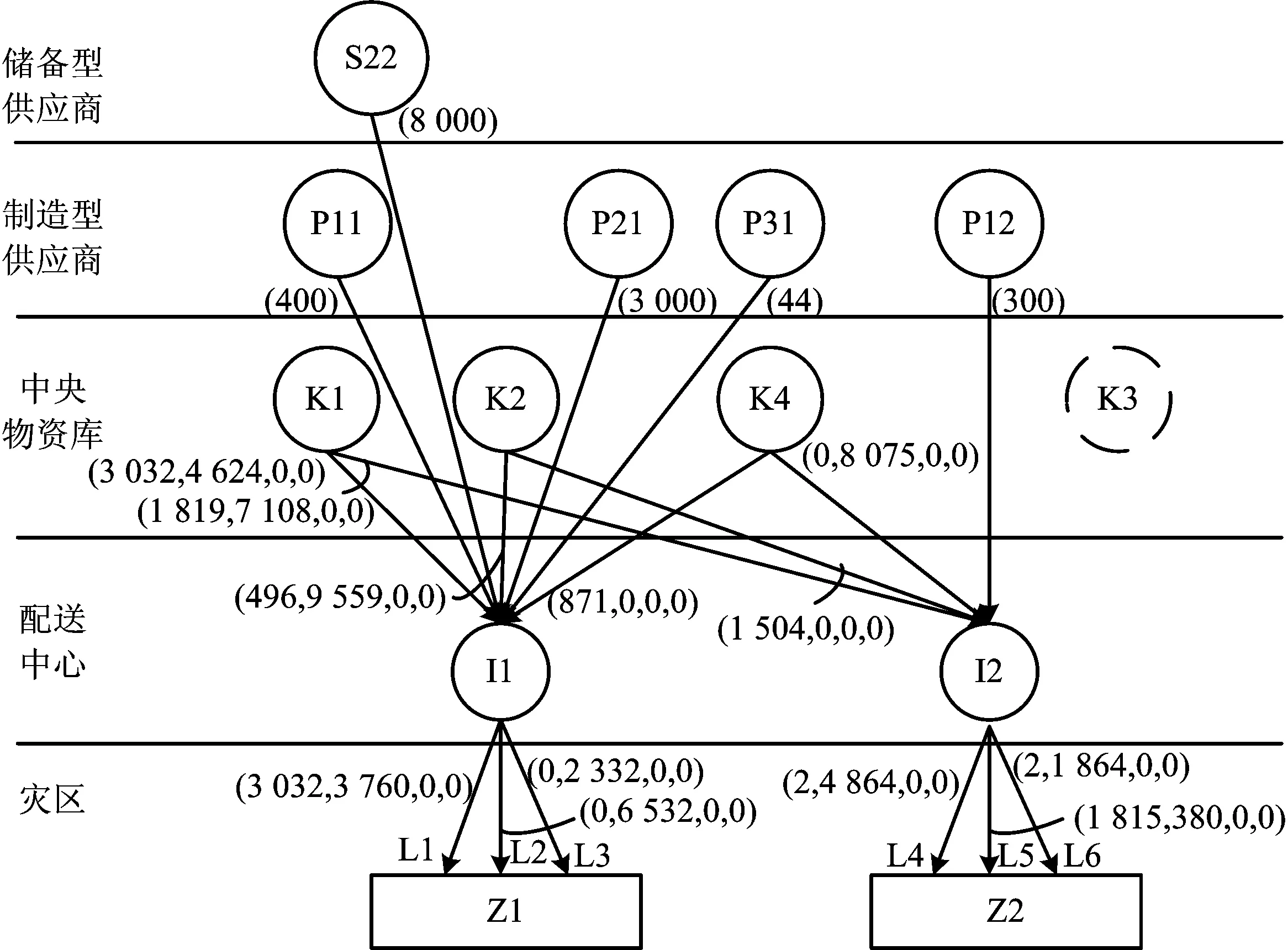
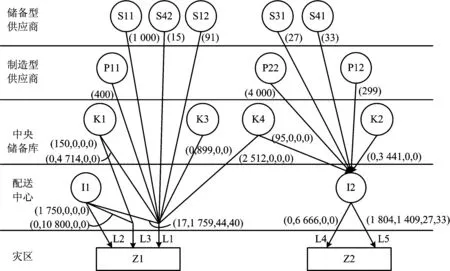
3.3 多供應主體模式優勢分析
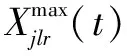


4 結論

