基于Hoek-Brown強度準則的隧道圍巖松動圈分析*

王　睿，袁崠洋，張進增，楊　俊

(1.西安理工大學 土木建筑學院，西安 710048; 2.西安工業大學 建筑工程學院，西安 710021; 3. 中鐵十八局集團第五工程有限公司，天津 300222)

0　引言

1907年俄國學者普羅托齊雅科諾夫[1-2]提出了自然平衡拱理論，將冒落拱內破碎巖體的重量當作支護外載，這成為了圍巖松動圈理論的雛形。之后的幾十年國內外學者通過現場觀測、模型試驗、理論分析、數值計算等手段對圍巖松動圈展開了深入研究，并于1985年由董方庭[3]總結了松動圈圍巖穩定性分類方法，并正式提出了松動圈支護理論。在隧道設計階段運用彈塑性理論分析松動圈分布范圍，是一種較為準確的方法。早期基于Mohr-Coulomb準則的芬納公式和卡斯特奈公式對理想的彈塑性體有較好的適用性[4]。之后，潘陽[5]、錢增幫[6-7]、翟所業[8]、胡小榮[9]、孟龍[10]等運用不同的巖石強度準則通過求解塑性區應力狀態和半徑，得出了在側壓力系數為1時圓形巷道圍巖松動圈的半徑。但由于圍巖巖性和地質構造的復雜多變，圍巖側壓力系數很難等于1，使得巖體塑性區應力狀態和松動圈半徑在不同方向具有一定差異，且物理力學參數難以準確測定，使得理論計算得到的結果不夠準確。故本文以彈塑性理論計算為基礎，利用H-B強度準則推導圍巖松動圈厚度的計算公式，并以某公路隧道為工程實例，結合理論計算和圍巖深部位移量測，分析了圍巖松動圈厚度，以期為初期支護錨桿的長度設計提供科學依據。

1　Hoek-Brown強度準則的提出與發展

1980年E. Hoek和E.T .Brown[11-13]在對大量巖石三軸試驗資料和巖體現場試驗成果的統計分析基礎上得出了巖石破壞時極限主應力間的非線性經驗關系，稱之為H-B強度準則，其表達式為：

(1)

式中：σ1，σ3分別為最大、最小壓應力，MPa；σci為巖石單軸抗壓強度， MPa；mi為巖石量綱反映巖石軟硬程度的經驗參數。

1992年E. Hoek等[14]對H-B準則進行了改進，使得該準則可同時適用于巖石和巖體，稱之為廣義H-B強度準則，其表達式為：

(2)

式中：mb，a為針對不同巖體的量綱經驗參數；s反映巖體的破碎程度。

之后，E. Hoek[15-18]等引入應力釋放的擾動參數D，并提出了基于地質強度指標(GSI)的巖體參數mb，s，a的取值方法：

(3)

2　基于H-B準則的圍巖松動圈厚度彈塑性分析

彈塑性分析的基本假設：隧道為圓形斷面，且在無限長的隧道長度內圍巖性質一致；圍巖為均質、各向同性的線彈性體，無蠕變性或黏性行為；初始地應力為自重應力，且為各向等壓狀態即假設側壓系數λ=1。

2.1　圍巖的塑性區應力

計算簡圖如圖1所示。

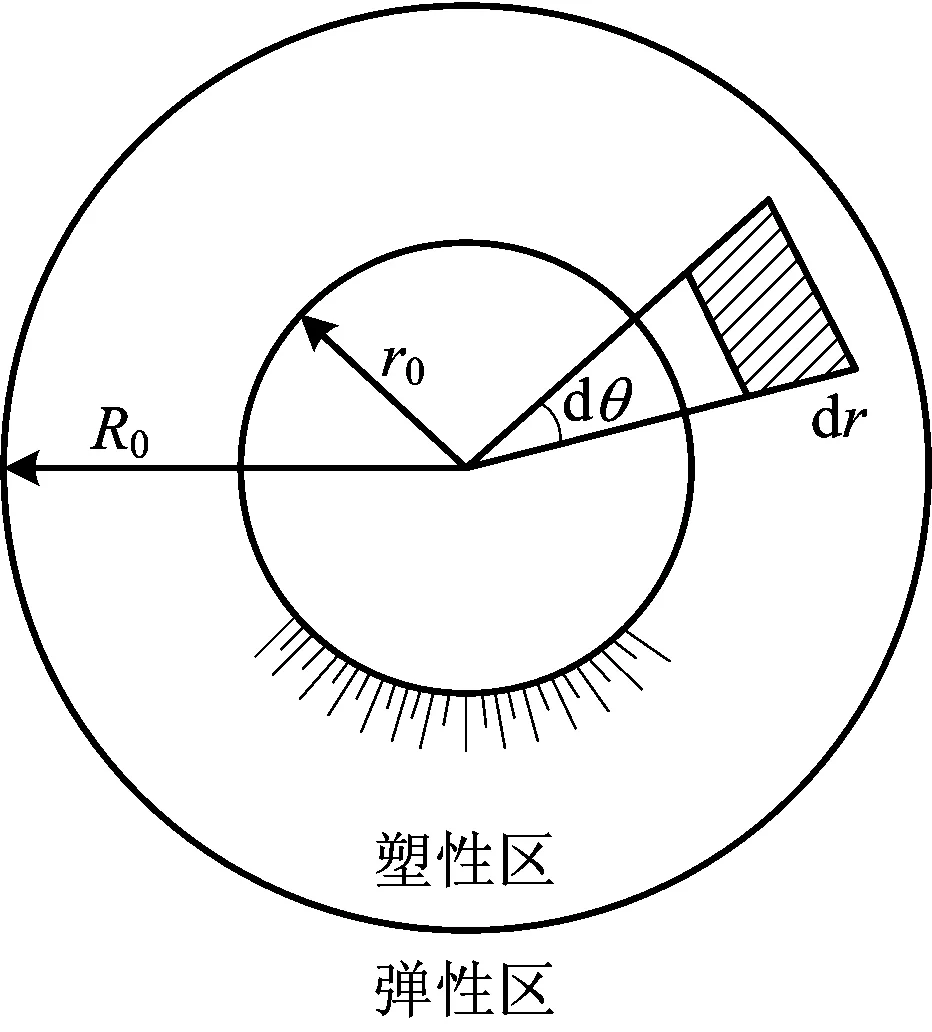
圖1　塑性區計算簡圖Fig.1　Calculation of the plastic zone diagram

此力學模型是軸對稱模型，在極坐標平面內應力分量僅為r的函數，不隨θ而變，切應力τθr=0。所以軸對稱平衡方程為：

(4)

式中：σr是徑向應力；σθ是切向應力。

而H-B強度準則為：

(5)

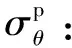
(6)

(7)

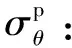
(8)

(9)

塑性區應力大小與mb，s，σci，pi，r，a，r0有關，其中mb，s，σci，a為巖體本身性質；pi為支護力；r為距巷道中心距離；r0為巷道半徑。

2.2　圍巖的彈性區應力

根據內外應力邊界條件以及位移單值條件可得圓筒受均布壓力的解答：

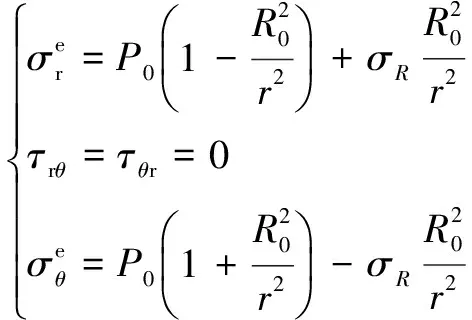
(10)

式中：p0為原巖應力；σR為彈塑性邊界處的徑向應力。

2.3　塑性區的半徑R0和松動圈半徑R

在彈塑性交界面上(r=R0時)，應有：

(11)

在彈性區內有：

(12)

當圍巖存在支護力Pi時，在r=R0時有：

(13)

(14)

(15)

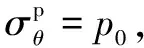
(16)

即可求出松動圈半徑R。

由于工程實踐中隧道斷面并不是標準圓形，且圍巖巖性和地質構造的復雜多變也無法確保側壓力系數λ=1，故簡單套用上述公式求得的松動圈分布范圍未能體現不同方向上的差異，特別是未能體現豎直方向和水平方向的差異。應在計算中將實測的豎直方向和水平方向初始地應力值分別代入上述公式，求出豎直方向和水平方向的松動圈范圍，同時還應通過現場實測，驗證計算結果的可靠性。

3　工程實例

銅旬高速某隧道位于銅川市照金鎮某村二組西約400 m，為雙洞單向雙車道分離式隧道。左線起訖樁號ZK203+220～ZK205+950，長度2730 m，最大埋深240 m；右線起訖樁號YK203+180～YK205+940，長度2 760 m，最大埋深239 m。

選取該隧道ZK204+930斷面為例，該斷面為IV類圍巖，圍巖為中風化的礫巖，雜色，礫狀結構，層狀構造，泥鈣質膠結，礫石成分以砂巖、石英砂巖為主，粒徑一般20～50 mm，最大約80 mm，節理裂隙較發育，巖芯呈柱狀，節長一般50～350 mm，RQD=80%。

隧道建筑限界：凈寬10.50 m，凈高5.0 m。設計內輪廓拱墻部分為內半徑R=5.57 m的單心圓，仰拱內半徑為15.0 m；最大開挖線12.88 m。凈空斷面設計如圖2所示。

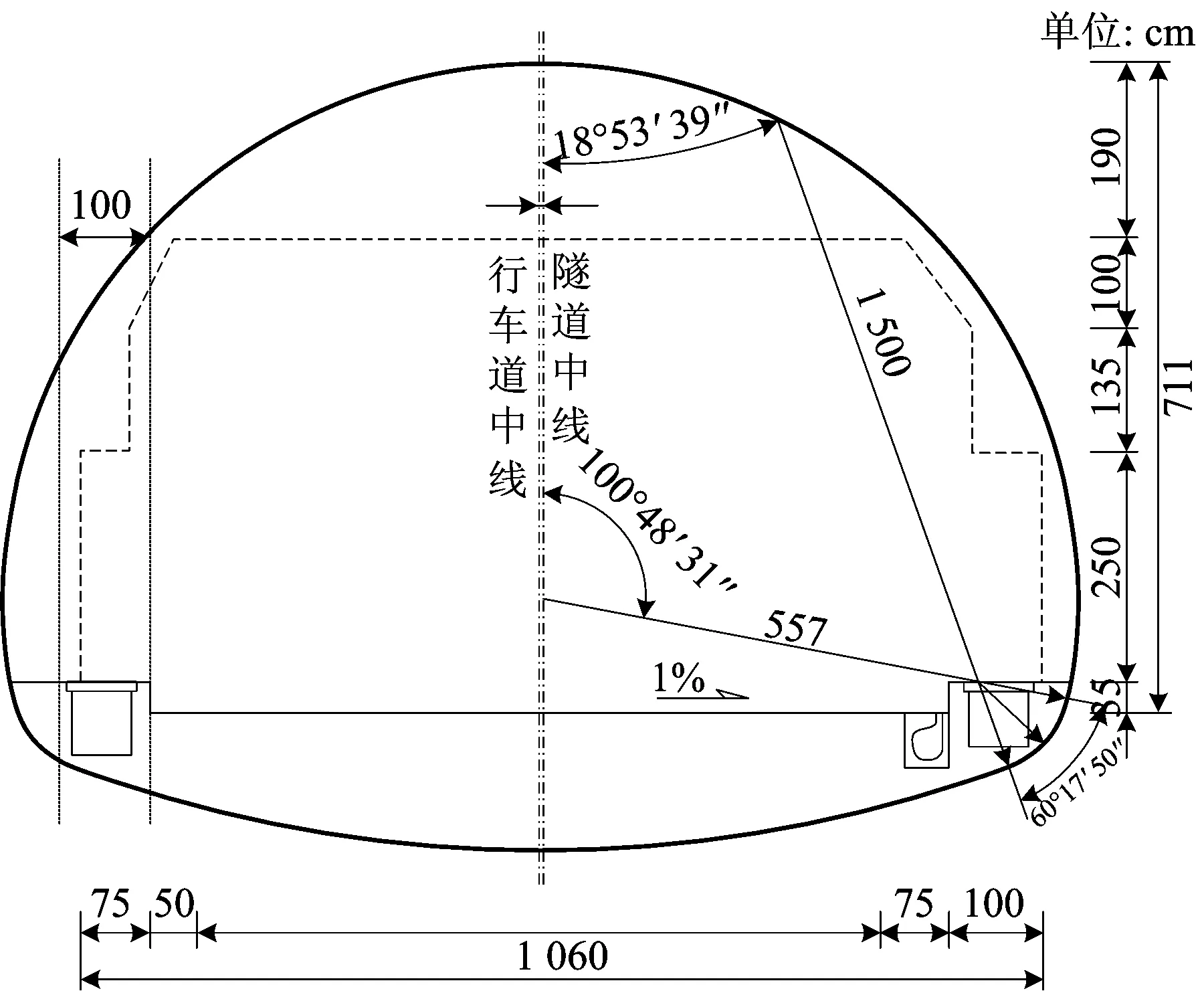
圖2　隧道凈空斷面Fig.2　The tunnel clearance section

經初步設計后，隧道支護參數見表1所列，圍巖的物理力學參數見表2。

表1　隧道支護設計參數

表2　隧道典型斷面參數選取

3.1　理論計算

初始地應力取自重應力，圍巖壓力按計算公式q=γh=24×0.45×2s-1[1+i(B-5)]，得q=0.147 MPa。根據《公路隧道設計規范(JTG D70-2004)》條文說明第9.2.5條，IV類圍巖中圍巖與初期支護承擔釋放荷載的比例為60%～80%，若取初期支護承擔圍巖壓力的80%時，則支護壓力約為0.1176 MPa，故假定支護壓力為Pi=0.1 MPa。

該隧道為單心圓設計，計算所選取的拱頂位置和邊墻水平位置均在此圓上，故適用于上述公式。同時公式是建立在側壓力系數λ=1的基礎上，而本工程中實測側壓力系數λ=0.4，為確保公式的適用性，在拱頂和邊墻水平位置分別取實際測算的地應力代入計算，既滿足公式要求，又真實反應出巖體的各向異性。

1)拱頂

初始地應力P0=γ·H=2.76 MPa，且已知r0=5.57 m，選用修正的GSI法進行參數求解，利用式(3)估算mb，s，a的值：

GSI=RMR-5=30

a=0.5

將以上參數代入式(14)式(15)，相加代入式(13)求得的塑性區半徑為：R0=7.83 m,塑性區的厚度為：

D0=R0-r0=7.83-5.57=2.26 (m)

再將以上參數代入式(16)求得松動圈半徑為：R=6.47 m,松動圈的厚度：

D=R-r0=6.74-5.57=1.17 (m)

2)邊墻水平位置

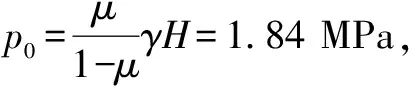
塑性區半徑：R0=7.12 m

塑性區的厚度：D0=7.12-5.57=1.55 (m)

松動圈半徑：R=6.12 (m)

松動圈的厚度：D=6.12-5.57=0.55 (m)

綜上，可得該斷面拱頂處圍巖松動圈位置約在1.17 m，而兩側邊墻處松動圈位置約在0.55 m處。

3.2　現場監測

在銅旬高速某隧道ZK204+930斷面拱頂中央及起拱線兩側(即A、B、C點處)，共布設3臺多點位移計監測圍巖深部位移。拱頂處A點，孔深5 m，共布置8個測點，分別為0.8 m，1.2 m，1.6 m，2.0 m，2.5 m，3 m，4 m，5 m；起拱線兩側B、C點，孔深3 m，各布置6個測點，分別為0.8 m，1.2 m，1.6 m，2.0 m，2.5 m，3 m。具體布置如圖3。

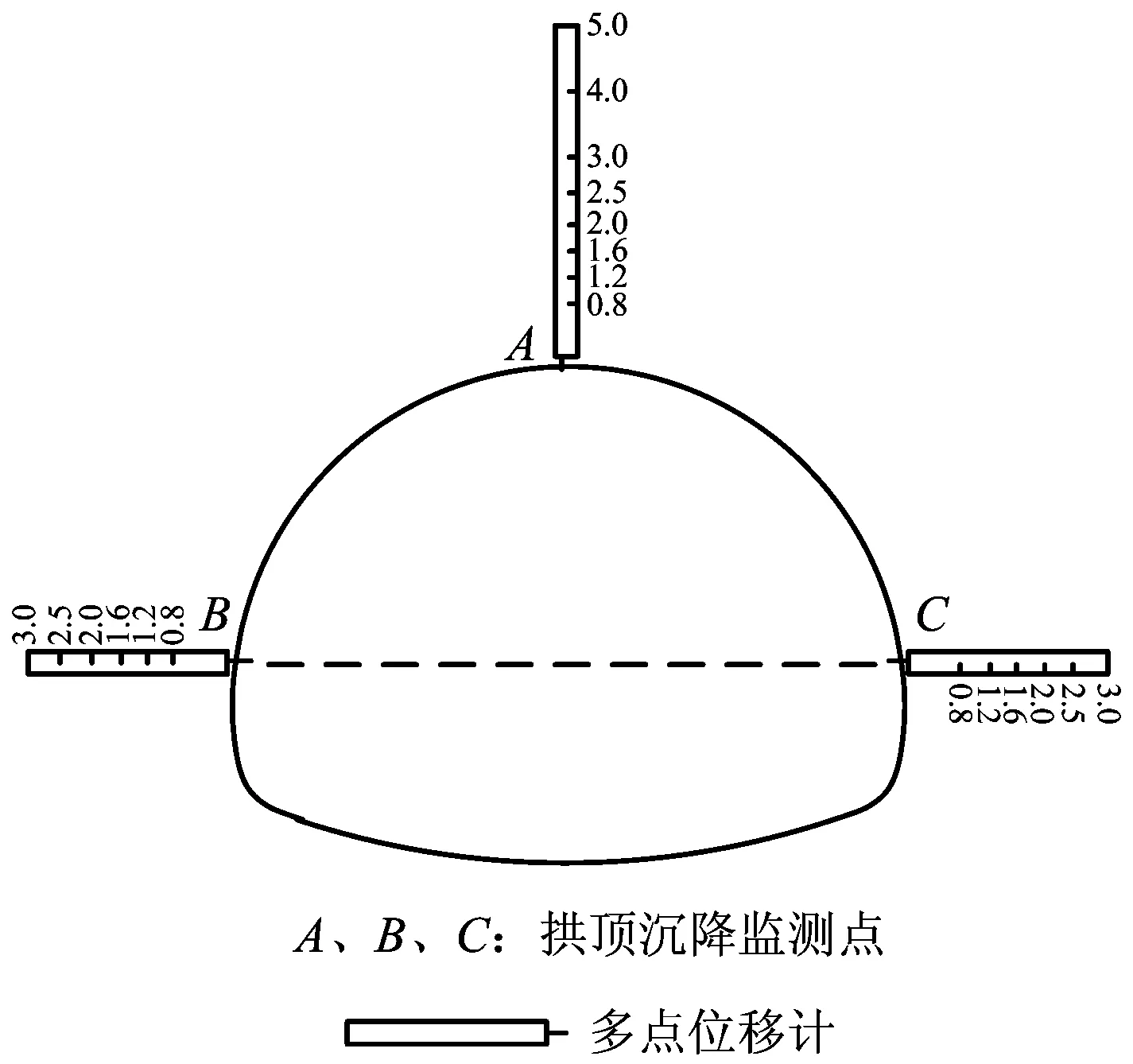
圖3　圍巖深部位移量測斷面布置Fig.3　Displacement measurement section plan

將斷面ZK204+930圍巖深部位移監測結果繪制成時態曲線，如圖4～圖7所示。

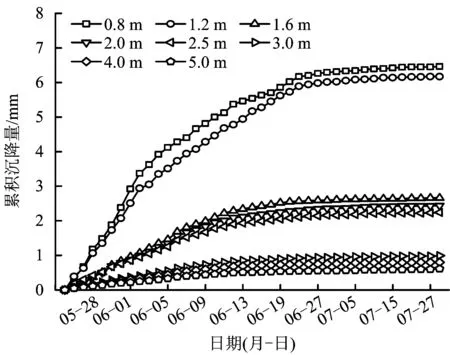
圖4　K204+930斷面A點圍巖深部位移時態曲線Fig.4　ZK204 +930 section point A displacement of deep surrounding rock temporal curves

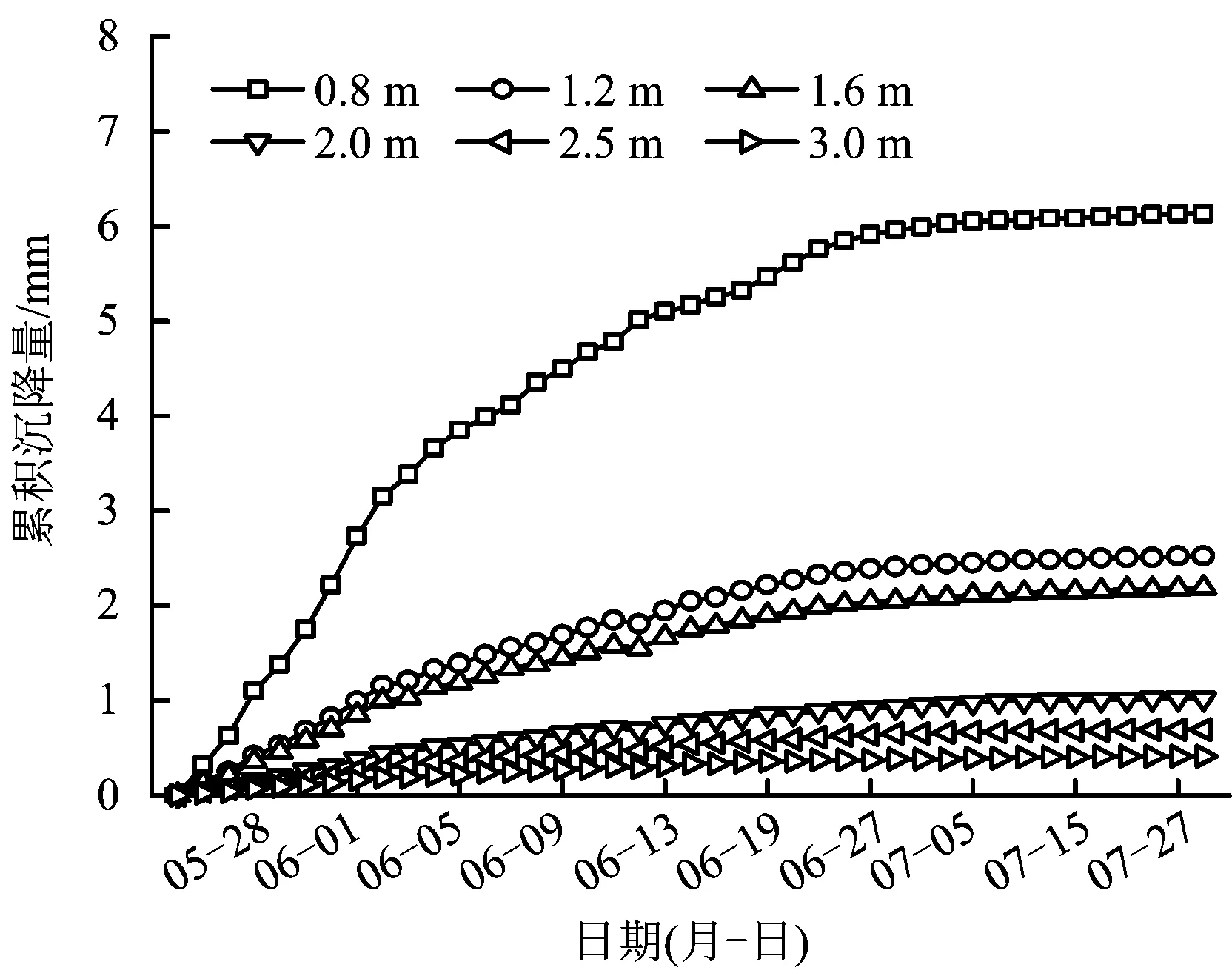
圖5　ZK204+930斷面B點圍巖深部位移時態曲線Fig.5　ZK204+930 section Point B displacement of deep surrounding rock temporal curves

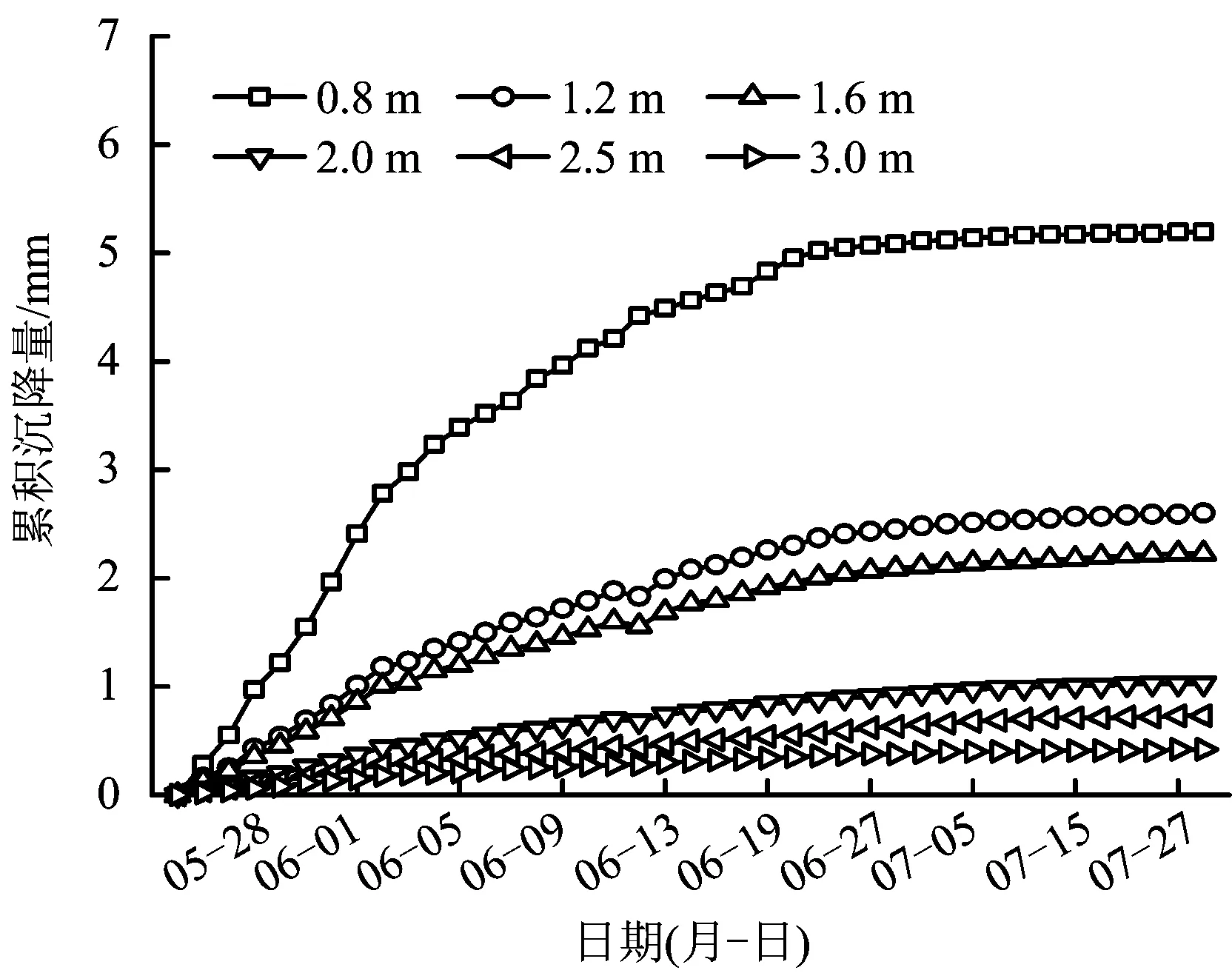
圖6　ZK204+930斷面C點圍巖深部位移時態曲線Fig.6　ZK204 + 930 section Point C displacement of deep surrounding rock temporal curves

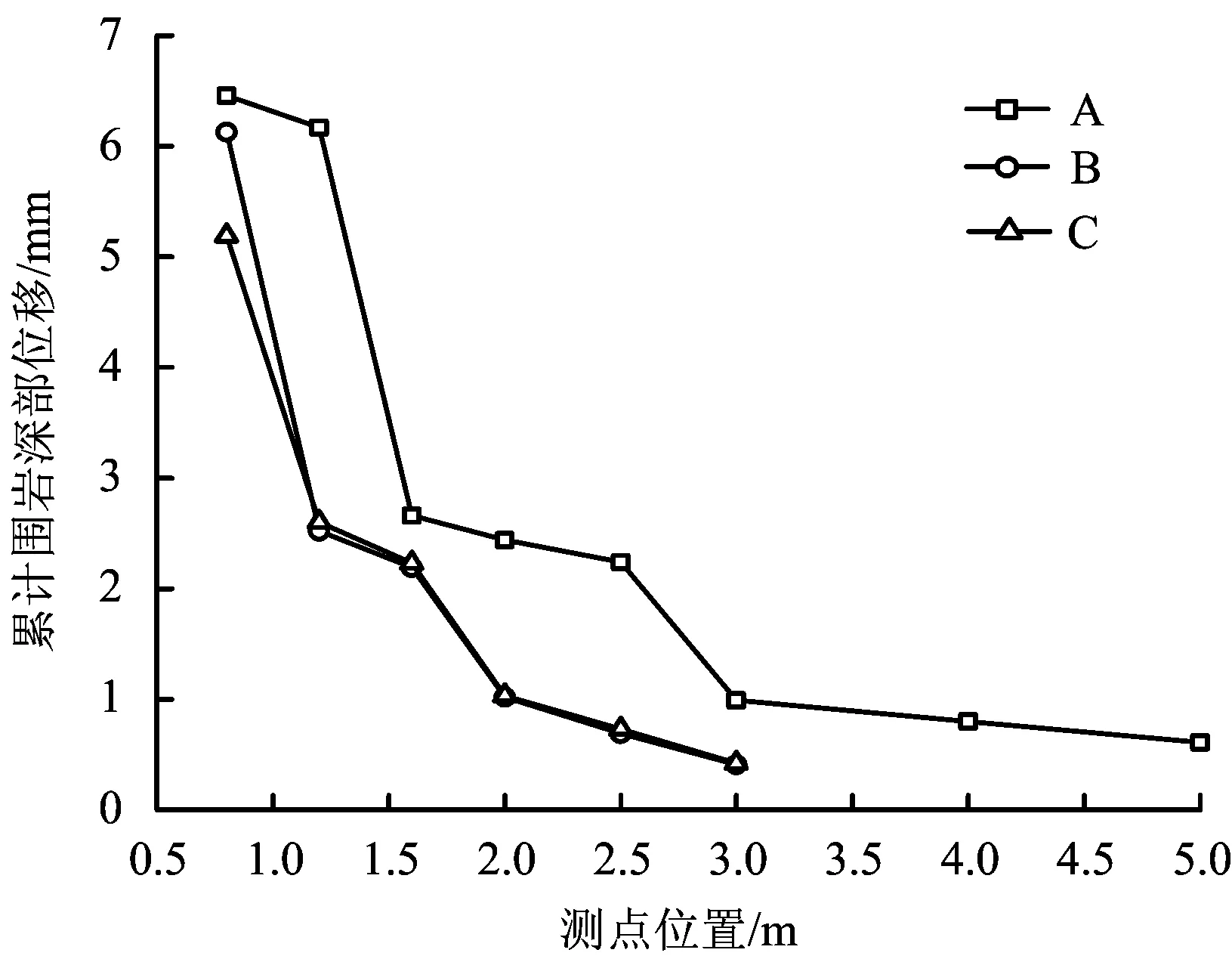
圖7　圍巖內部位移曲線Fig.7　Internal displacement curve of surrounding rock

由圖4可知，隨著時間的推移，圍巖深部各點位移有不同程度的增加，其中最接近洞頂的1號點累積位移量最大為6.46 mm；2號點累積位移量為6.17 mm；8號點距洞頂最遠，位移量最小僅0.61 mm。從總的趨勢來看，距洞頂越近，受開挖影響越大。從圖4可直觀地看出，圍巖深部位移累積量可分為3個層次，1號點和2號點為第一層次，厚度約1.60 m，該區受開挖影響最大，支護時錨桿長度應穿過該區；3號點至5號點為第二層次，該區厚度約為1.4 m，為開挖次影響帶；6號點至8號點是最外區，基本不受開挖掘進影響。故該斷面拱頂處松動圈在2號點和3號點之間，即1.2～1.6 m處；塑性區在5號點和6號點之間，即2.5～3.0 m處；6號點之外，即3.0 m之外為彈性區。同理，由圖5，圖6可得在該斷面邊墻位置松動圈在1號點和2號點之間，即0.8～1.2 m處；塑性區在3號點和4號點之間，即1.6～2.0 m處；4號點之外，即2.0 m之外為彈性區。

根據圍巖內部位移曲線判斷松動圈的依據是：如果位移曲線斜率可以分為3個區域，那么靠近圍巖壁面的位移量最大是松動區；位移量較大的區域為應力升高區；再往圍巖深部變形量最小為彈性區[19]。故由圖7可得，A，B，C3個測點的圍巖內部位移曲線按斜率大小均可分為3個區段，A點拱部松動圈位置在1.2～1.6 m處，塑性區位置在2.5～3.0 m之間，3.0 m之外為彈性區；B，C點邊墻處松動圈位置在0.8～1.2 m處，塑性區位置在1.6～2.0 m之間，2.0 m之外為彈性區。

3.3　小結

銅旬高速某隧道ZK204+930斷面處，圍巖級別為IV級，假定支護壓力為0.1 MPa時，以彈塑性理論為基礎，利用H-B強度準則推導圍巖松動圈厚度的計算公式求得松動圈厚度和運用多點位移計進行圍巖深部位移量判定的圍巖松動圈范圍結果見表3。

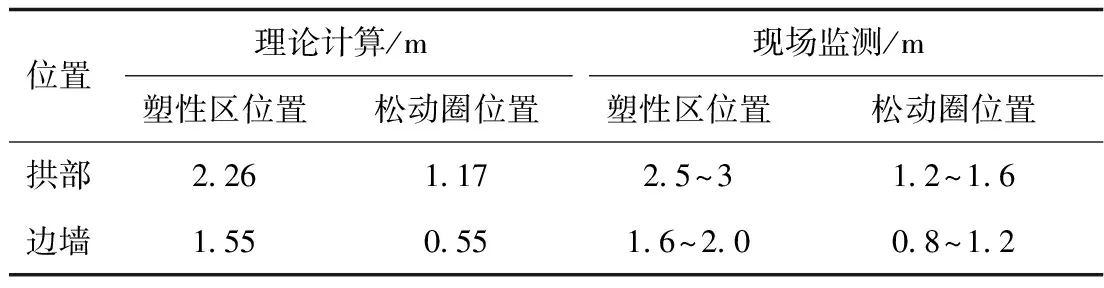
表3　分析結果對比

理論計算與現場量測結果進行比較可知，在進行圍巖松動圈厚度計算上2種方法的結果在拱頂位置基本保持一致，而在邊墻位置理論計算值略小。分析說明利用H-B強度理論推導的圍巖松動圈厚度計算公式，在實際公路隧道中計算圍巖的松動圈厚度具有一定的準確性和適用性。

4　結論

1)以彈塑性理論為基礎，應用H-B強度準則，推導的方程組能較為準確的計算公路隧道圍巖松動圈的厚度，特別是圓形硐室時準確性較高。但計算參數的選取，特別是圍巖的m，s，a數值的準確性亟待提高。

2)隧道圍巖松動圈的分布不僅與圍巖的級別有關，而且還與支護力的大小有著密切的關系。隨著支護力的增加，松動圈的范圍是逐漸減小的；隨著圍巖級別變差，松動圈的范圍是逐漸增大的。

3)由于隧道橫斷面形狀并非標準圓形，且圍巖初始應力具有明顯的方向性，故松動圈在橫斷面上的分布是不規則的，多呈現出拱頂松動圈厚度大于水平向的趨勢。根據實測側壓力系數值，分別求得不同方向的圍巖松動區范圍可較為真實的反映其分布規律。

[1]徐干成，白洪才，鄭穎人，等.地下工程支護結構[M].北京：中國水利水電出版社，2001.

[2]史興國.巷道圍巖松動圈理論的發展[J].河北煤炭，1995，4(1)：1-5.

SHI Xingguo. Development of theory based on broken rock zone[J]. Hebei Coal，1995，4(1)：1-5.

[3]董方庭，等.巷道圍巖松動圈支護理論及應用技術[M].北京：煤炭工業出版社，2001.

[4]蔡美峰，何滿朝，劉東燕. 巖石力學與工程[M].北京：科學出版社，2013.

[5]潘陽，趙光明，孟祥瑞，等.基于Hoek-Brown強度準則的巷道圍巖彈塑性研究[J].工程地質學報，2011，19(5)：637-641.

PAN Yang，ZHAO Guangming，MENG Xiangrui. et al. Elasto-plastic reseach of surrounding rock based on Hoek-Brown strength criterion[J]. Journal of Engineering Geology, 2011, 19(5): 637-641.

[6]曾錢幫，王恩志，王思敬. Hoek-Brown破壞準則求解圓形硐室塑形區半徑與修正的芬納公式比較[J].沈陽建筑大學學報(自然科學版)，2008，24(6)：933-938.

ZENG Qianbang , WANG Enzhi, WANG Sijing. Comparison between plastic radius around a circular opening derived from Hoek-Brown failure criterion and calculated through modified Fenner Formula[J]. Journal of Shenyang Jianzhu University (Natural Science), 2008, 24(6)：933-938.

[7]曾錢幫，王思敬. 運用Hoek-Brown經驗準則分析圓形硐室圍巖彈塑性應力和位移[J]. 工程地質學報，2007，15(6)：757-761.

ZENG Qianbang, WANG Sijing. Elastro-Plastic analysis of stresses and displacements around a circular opening using the HoekBrown empirical critetion[J]. Journal of Engineering Geology.2007，15(6)：757-761.

[8]翟所業，賀憲國.巷道圍巖塑性區的德魯克-普拉格準則解[J].地下空間與工程學報，2005，2(1)：223-226.

ZHAI Souye，HE Xianguo. Solution of D-P criterion of plastic district of surrounding rock of roadway[J]. Chinese Journal of Underground Space and Engineering, 2005，2(1)：223-226.

[9]胡小榮，周洪華，胡昌斌.雙剪統一強度準則改進及其在巖土工程中的應用[J].巖土力學，2004，25：97-102.

HU Xiaorong，ZHOU Honghua，HU Changbin. Improvement of double shear criterion and its applications to geotechnical engineering[J]. Rock and Soil Mechanics, 2004，25：97102.

[8]HOEK E，BROWN E T.Empirical strength criterion for rock masses[J]. Journal of Geotechnical and Geoenvironmental Engineering， ASCE， 1980，106(9)：1 013-1 035.

[10]孟龍，高召寧，孟祥瑞.考慮損傷的圓形巷道圍巖彈塑性分析[J].中國安全生產科學技術，2013，9 (11)：11-16.

MENG Long，GAO Zhaoning，MENG Xiangrui. Elasto-plastic analysis of circular roadway surrounding rocks under consider ation of rock damage[J]. Journal of Safety Science and Technology, 2013，9 (11)：11-16.

[11]HOEK E，BROWN E T. Underground excavations in rocks[M].London：Institution of Mining and Metallurgy，1980：527.

[12]HOEK E,BROWN E T. Practical estimates of rock mass strength [J].International Journal of Rock Mechanics and Mining Sciences，1997，34(8)：1165-1186.

[13]MARINOS P，HOEK E.Estimating the geotechnical properties of heterogeneous rock masses such as flysch[J]. Bulletin of Engineering Geology and Environment，2001，60(2)：85-92.

[14]HOEK E，WOOD D，SHAH S.A modified Hoek-Brown criterion for jointed rock masses[A]. HUDSON J A ed. Proceedings of the Rock Characterization，Symposium of ISRM[C]. London：British Geotechnical Society，1992：209-214.

[15]Hoek E，Brown E T.The Hoek -Brown failure criterion[A]. Curran JH.Proc.15th Canadian Rock Mech Symp[C]. Toronto：Civil Engineering Dep.t，University of Toronto，1988：31-38.

[16]HOEK E. Strength of rock and rock masses[J]. International Society for Rock Mechanics News Journal，1994，2(2)：4-16.

[17]HOEK E，KAISER P K，BAWDEN W F.Support of underground excavations in hard rock[M]. Rotterdam：A. A. Balkema，1995：99.

[18]HOEK E，CARRANZA-TORRES C，CORKUM B.Hoek-Brown failure criterion-2002 edition[A]. HAMMAH R,BAWDEN W F，CURRAN J，et al.ed. Proceedings of the North American Rock Mechanics Society NARMS-TAC 2002[C].Toronto ：University of Toronto Press，2002：267-273.

[19]李曉紅.隧道新奧法及其量測技術[M].北京：科學出版社，2002.