基于脆弱性的地鐵網絡事故蔓延模型構建研究*

許　葭，宋守信，翟懷遠，陳明利

(北京交通大學 經濟管理學院，北京 100044)

0　引言

通常意義上，只有當事故或災害不可避免時，我們才會相對應的采取一定的應急救援工作來防止事故蔓延并減輕危害后果，但是無論是從應急救援的管理思路[1-2]，還是具體實施上[3]，我們的著眼點仍然集中在事故發生點。然而，隨著現代社會的不斷發展，社會中各部分不再僅僅是以單一個體存在，更多的呈現出系統化、互聯化的特色，特別是新興的地鐵系統，牽一發而動全身，正因為如此，迫切需要能與之相切合的科學應急管理方案。為此，首要任務就是針對網絡化地鐵系統事故蔓延的機理開展研究。

事實上，風險的傳遞[4]、輿論的傳播[5]、事故的蔓延等多種網絡條件下的蔓延動力學已經成為研究熱點[6]，近些年來更是成果頗多，例如：文獻[7]結合主動網絡節點，雙穩態元素和鏈路延遲交互的特征，提出故障傳播動力學模型；文獻[8]針對供水系統、供電系統、交通系統的共同特征，建立1個普適性的災害蔓延動力學模型，主要涉及網絡結點的自修復功能、災害蔓延機制和內部隨機噪聲3個重要特征參數；文獻[9]基于另1個普適性的災害蔓延動力學模型，對3種網絡拓撲結構(隨機網、小世界網和無標度網)進行仿真，結果顯示3種網絡表現出不同的脆弱程度，并獲得實例驗證。

總結以上研究結果，更多關注的是整個系統的運行狀態，是相對宏觀的角度，但是在安全領域，特別是應急措施的制定，則更需要關注節點自身的層面。因此，針對地鐵節點數量少，且網絡平均度小的特點，有針對性提出在地鐵網絡上事故蔓延的機理，并據此完成模型構建。

1　原理闡述

1.1　脆弱性

脆弱性研究起源于環境科學[10]領域，隨后擴展到電網、交通等多個領域，對于脆弱性概念，不同研究領域的認識相對統一，即脆弱性是個概念的集合，既考慮系統內部條件對脆弱性的影響[11]，也包含系統與外界環境相互作用的特征[12]，具體而言，脆弱性有以下2個特點：

1)脆弱性是針對系統本身

脆弱性是系統本身的特質，它的著眼點不是系統中任何1個單一用戶，而是1個系統的整體。它不僅限于每個用戶個體的使用感受，不拘泥于系統中每個部件的完美運行，更多的是考慮作為1個整體的系統能否正常運行，所以從某種意義上來說，系統脆弱性可以看成是對系統可靠性的宏觀視角下的補充，而非對立存在。

2)脆弱性是復雜概念集合

隨著安全領域的不斷深入研究，僅僅針對單一事物的研究、評價已經遠遠不能滿足現在安全管理的需求，如何科學、準確表述復雜耦合系統下的安全現狀，是安全研究的難點和重點，脆弱性正是在此情況下被廣泛提及，并且被證明是有效的。脆弱性既需要考慮系統內部條件對系統脆弱性的影響，也包含系統與外界環境相互作用的特征，所以脆弱性是1個包含了系列相關概念的概念集合，各個概念間也不是簡單的疊加，彼此之間存在著復雜的耦合關系。

脆弱性的以上特性，使得使用脆弱性概念來全面刻畫地鐵的安全狀態，特別是用來考慮事故的蔓延，是可行的。

1.2　事故蔓延機理

在網絡化的情況下，各節點間不再是孤立存在的，而是存在著緊密的相互聯系。因此，事故一旦在網絡中發生，那將不可避免地沿著網絡拓撲結構進行蔓延，如圖1所示。

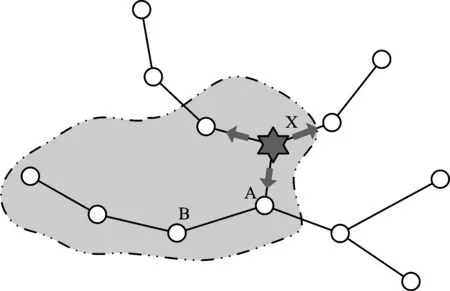
圖1　網絡事故蔓延示意Fig.1　Schematic of failure propagationin network

也就是說，事故點會對整個網絡系統中的所有站點產生影響，這是地鐵事故蔓延機理的1個特點—普遍性。

與此同時，網絡中事故蔓延的基本原則毫無疑問是拓撲距離的遠近[13]，離事故點最近的節點，譬如圖1中的節點A與節點B，節點A必定會先受到影響，之后影響節點B。換言之，事故點產生的影響并不是同時發生，而是根據路徑的長短，存在一定的先后順序，這是地鐵事故蔓延機理的另1個特點—順序性。但是否會在節點A處引發事故，就需要考慮節點A本身的性質，也就是節點A的脆弱性。

根據上述的思路，事故在節點X發生，首先影響離事故初發點X的拓撲距離為1的所有節點的集合，其次為拓撲距離為2的節點，并逐步擴散至整個網絡。如果被影響節點的脆弱性足夠低，那么這些擾動就會在節點里逐漸被吸收；反之，如果此時節點的脆弱性較高，那么擾動就會外在表現出來，影響站點的運營狀態，最終出現在圖1中顯示的深色事故區域。因此，在地鐵網絡上，事故蔓延呈現出第3個特點—指向性，也就是事故的發展不是均勻的，而是傾向于往脆弱性大的站點蔓延。

2　模型構建

2.1　引力模型

17世紀牛頓提出著名的萬有引力定律，由此牛頓物理學問世。萬有引力定律給物理學及許多自然科學學科的發展以劃時代的推動。根據該定律，任何2個物體之間的作用(引力)的大小與它的質量成正比，與它們之間的距離平方成反比。引力模型是以牛頓經典力學的萬有引力公式為基礎，應用廣泛的空間相互作用能力模型，即用來分析和預測空間相互作用能力的數學模型，目前已被廣泛應用到各種學科領域中，其中比較常見的是國際貿易學說。Tinbergen(1962)和Poyhonen(1963)對其在經濟學領域做了發展、延伸，模型在以后很多學者的實證分析方面也得到成功印證。同時，隨著經濟地理學家的關注，引力模型被廣泛應用于各類相關研究中。引力模型的1個重要特點，是它的基本形式保持不變，只要對參數和分量的定義作出適當的改變，就可將引力模型應用于不同的問題。

地鐵網絡事故的蔓延可以看成站點脆弱性間的引力效應，脆弱性大的站點對于事故初發點之間的吸引力大，引導事故向脆弱性大的地方發展，根據前文提出的3個特點，也符合引力模型的相關結論，所以基于引力模型，構建地鐵網絡事故蔓延模型。

2.2　地鐵網絡事故蔓延模型

在地鐵系統中，相對于火災等傳統意義上的事故而言，更頻繁出現的則是與客流壓力相關的事故，例如站點的封站、停運或者通過不停車等。在我國，很多地鐵線路長期處于超負荷運行狀態，此類事故看似影響不大，但是波及范圍廣、發生次數多，與此相對的則是安全管理上的忽視，極易產生重大的安全事故隱患。因此，基于引力模型計算地鐵網絡事故各站點兩兩間的引力值，此值可以反映出事故在2個站點間傳遞的難易程度，在此稱之為事故蔓延引力值。

將引力模型特別應用于地鐵網絡事故蔓延上，有針對性地對相應的參數進行修改。首先，上文已經闡述脆弱性在表征安全狀態，特別是地鐵安全狀態時的重要性，所以在地鐵網絡事故蔓延的引力模型中，使用脆弱性代替質量；其次，關于節點間的距離，在模型中采用地鐵實際運營的區間時間，因為在地鐵系統中，一方面由于固定的軌道和隧道限制，地鐵客流不存在路徑上的流失，必然是從節點到節點，另一方面，地鐵車輛的運營速度也是存在差異的，所以節點間的區間時間更能說明站點間的互聯狀態。因此，基于引力模型，構建地鐵網絡事故蔓延模型，如式(1)所示。

(1)

其中：Fxi為站點i和事故初發點X之間的事故蔓延引力值；VX,Vi分別為事故初發點X和站點i的脆弱性值；tXi為站點i到事故初發點X的最短時間；K為引力系數，在這里選取為1；a,b分別為事故初發點X和站點i對事故蔓延的潛力指數。

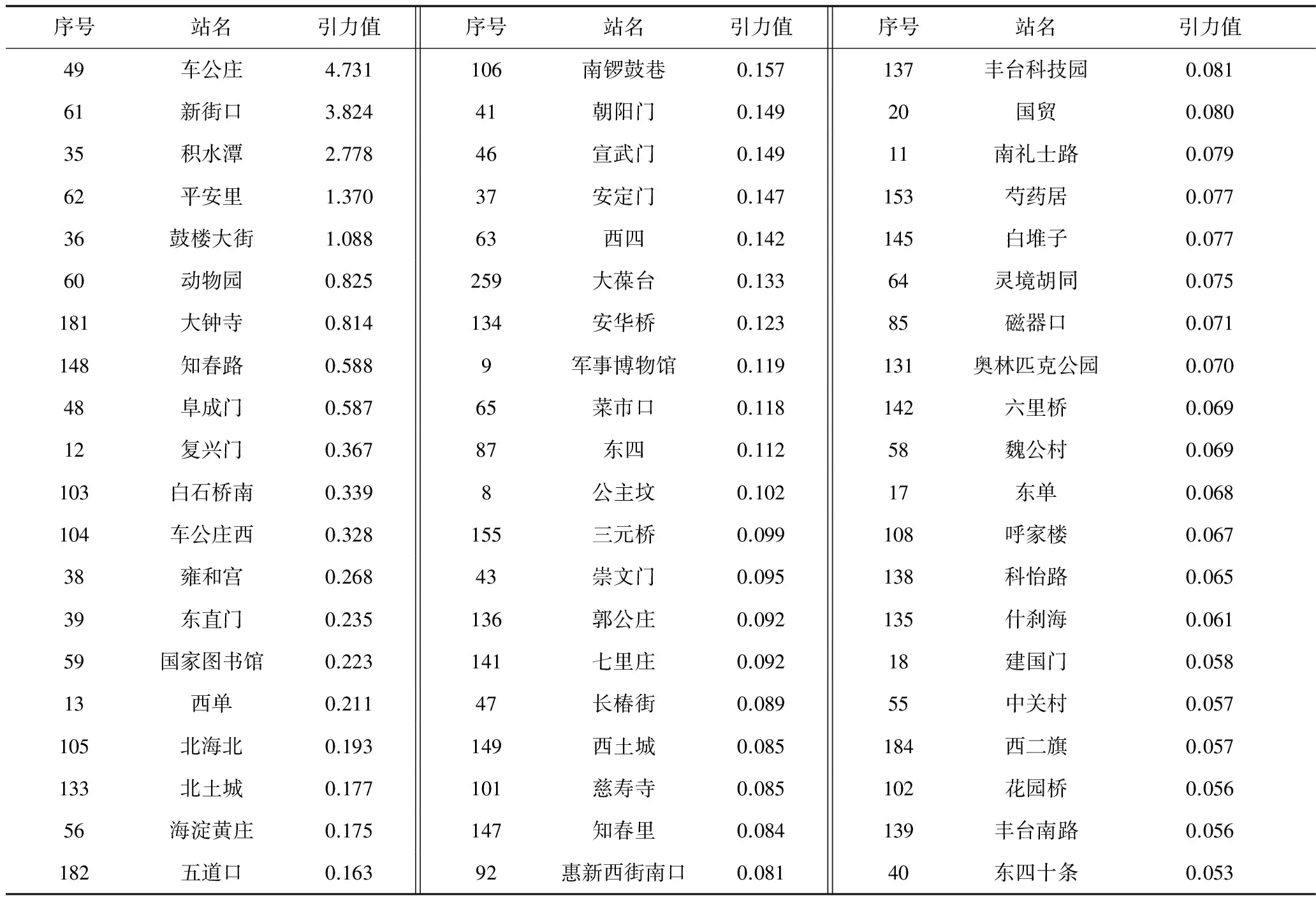
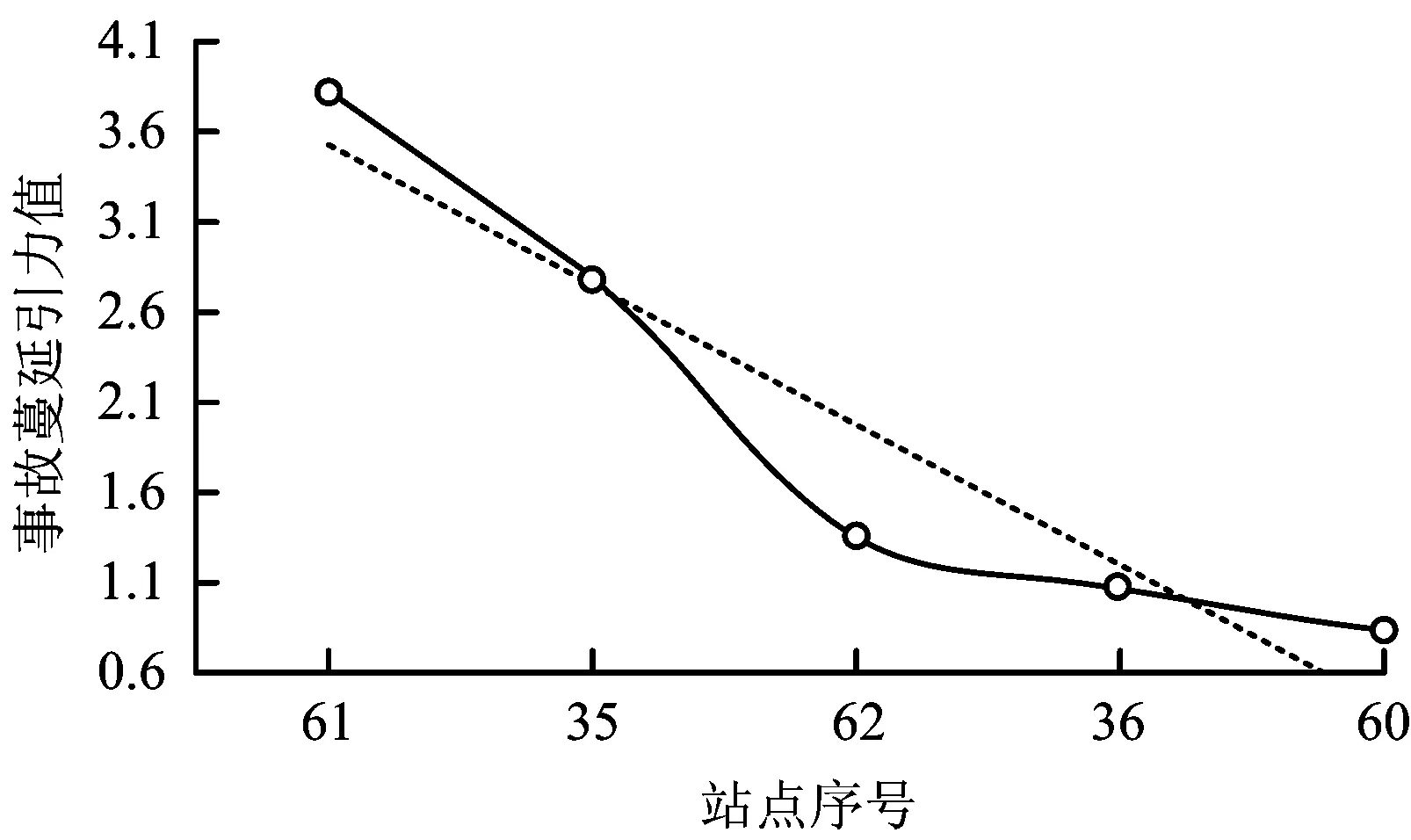
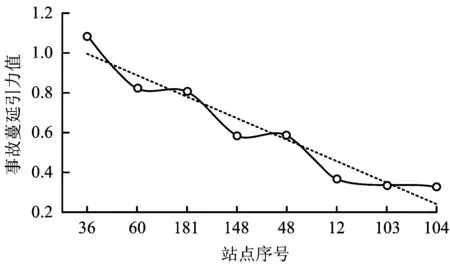
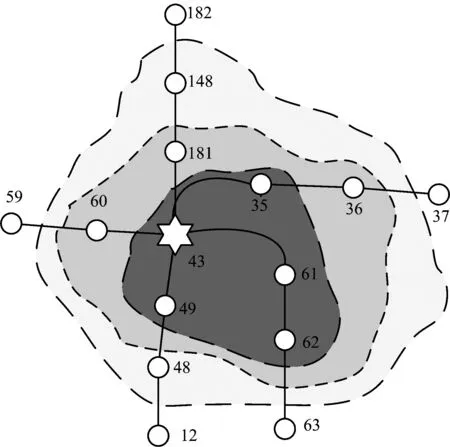
對于事故初發點X和站點i，在不同情況下，對事故蔓延的吸引力不同，也就是潛力指數是不同的。當a>b時，說明事故傾向于聚集在初發點X處，換言之，事故點處的應急救援工作相對出色，抑制事故的蔓延；反之，當a

所以根據式(1)，可以得出在事故點X和網絡中各個站點之間的引力值大小，按照降序排列的方法繪制曲線，該曲線存在數個斷裂點，即在該點附近，微小的變化也會引起引力值較大的改變，換言之，在該點曲線的凹凸性發生變化。由此，該曲線也被分為若干個層次，據此得出事故蔓延到各個站點的層級順序，可有針對性地采取事故措施。

3　實例應用

以北京地鐵為例，截止2015年初，北京地鐵共有18條地鐵線路，共268個運營車站，其拓撲結構如圖2所示。

圖2　北京地鐵車站拓撲Fig.2　Topology of Beijing subway network

根據文獻[14]構建的脆弱性評價模型，可以得到北京地鐵各站點的脆弱性數值，由于篇幅限制，選取部分站點，如表1所示。

表1　部分北京地鐵車站脆弱性數值

假設站點西直門發生事故，則網絡中其余站點到達西直門站的最短時間，采用Floyd算法計算可得，部分數據如表2所示。以磁器口站為例，其到達西直門的最短時間為19 min，所采用的路徑為85(磁器口)→43(崇文門)→44(前門)→45(和平門)→46(宣武門)→47(長椿街)→48(阜成門)→49(車公莊)→34(西直門)。

表2　部分北京地鐵車站到達西直門站的區間時間

西直門處的脆弱性為3.371 4，明顯高于整網的平均值1.428 2，那么取a=1,b=2，根據式(1)可以得出各站點的事故蔓延引力值，如表3所示。為了方便觀察各站點事故蔓延引力值的變化情況，對各站點的事故蔓延引力值進行降序排列，與此同時，由于第34位的郭公莊(136，0.092)開始，引力值小于第1位的車公莊(49，4.731)的1.9%，之后的趨勢變化相對較小，因此，選取前33位的站點如圖3所示。

圖3　北京地鐵西直門事故蔓延引力值(降序)Fig.3　Failure propagate gravitation of Beijing subway(DESC)

表3　北京地鐵車站事故蔓延引力值(西直門)

圖4　北京地鐵西直門事故蔓延引力值(61-60)Fig.4　Failure propagate gravitation of Beijing subway(61-60)

圖5　北京地鐵西直門事故蔓延引力值(36-104)Fig.5　Failure propagate gravitation of Beijing subway(36-104)

圖6　西直門事故蔓延趨勢Fig.6　spreading tendency of Xi Zhimen accident

通過圖4和圖5明顯可以看到在站點62(平安里)、181(大鐘寺)和48(阜成門)處出現平穩趨勢后，產生較為明顯斷裂，所以可以據此將事故蔓延分為4個等級，如表4和圖6所示。

從上面的結果可以看出，對于同樣距離西直門站點拓撲距離為1的35(積水潭)、49(車公莊)、60(動物園)、61(新街口)和181(大鐘寺)5個站點就存在明顯差距，而在拓撲距離為2的站點中，62(平安里)則相對較為脆弱，甚至超過了部分拓撲距離為1的站點。另一方面，從圖6可以較為明顯的看出西直門站點的事故是向東南方向蔓延，這與現實的情況較為相符；與此同時，按照模型測算可知，當西直門站點發生客流事故時，需要采取應急響應的站點共有9個，數量較少，有利于制定專項的應急方案。

表4　北京地鐵西直門事故蔓延等級

4　結論

1)通過分析脆弱性的內涵特征，確定脆弱性為刻畫事故蔓延的特征參數，分析在網絡化條件下，地鐵事故沿拓撲結構的蔓延機理。

2)與傳統地鐵網絡應急簡單依靠地理距離劃分不同，根據網絡事故蔓延機理，構建基于脆弱性的地鐵網絡事故蔓延的引力模型，綜合考慮脆弱性、拓撲距離、地理距離等多方面因素，為網絡條件下客流事故的應急響應等提供相對合理的理論依據。

3)以北京地鐵為例，實例驗算西直門為初發站點的事故蔓延情況，確定車公莊、新街口、積水潭和平安里4個一級應急響應的站點；鼓樓大街、動物園和大鐘寺3個二級應急響應的站點；知春路和阜成門2個三級應急響應的站點。

4)建立的地鐵網絡事故蔓延引力模型的先決條件為網絡中的線路暢通，因而無法應用在火災等直接破壞線路運營的大型事故上，這將是下一步的重點研究方向。

[1]劉有飛, 蔡斌, 吳素農. 電網冰災事故應急處理及反思[J]. 電力系統自動化, 2008, 32(8):10-13.

LIU Youfei, CAI Bin, WU Sunong. Emergency management for the ice disaster in power grids and some sugges-tions[J]. Automation of Electric Power Systems, 2008, 32(8):10-13.

[2]高太光, 黃敏, 陳培友. 物聯網環境下煤礦救援資源調度多Agent自動協商模型[J]. 管理工程學報, 2016, 30(3):134-140.

GAO Taiguang, HUANG Min, CHEN Peiyou. Multi-Agent automated negotiation model of rescue resource allocation for coal mine accidents based on internet of things[J]. Journal of Industrial Engineering and Engineering Management, 2016, 30(3):134-140.

[3]龔迪琛, 方方, 陳智,等. 核電事故應急隨機網絡的粒子群優化分析[J]. 原子能科學技術, 2014, 48(5):898-902.

GONG Dichen, FANG Fang, CHEN Zhi, et al. Analysis in nuclear power accident emergency based on random network and particle swarm optimization[J]. Atomic Energy Science and Technology, 2014, 48(5):898-902.

[4]李存斌, 黃旻. 基于學習型貝葉斯網絡的供電風險傳遞分析[J]. 中南大學學報(自然科學版), 2011, 42(8):2338-2344.

LI Cunbin, HUANG Min. Power supply risk transmission analysis based on learning Bayesian networks[J]. Journal of Central South University, 2011, 42(8):2338-2344.

[5]Tsimring L S, Huerta R. Modeling of contact tracing in social networks[J]. Physica A Statistical Mechanics & Its Applications, 2003, 325(1-2):33-39.

[6]Helbing D, Kühnert C. Assessing interaction networks with applications to catastrophe dynamics and dis-aster management[J]. Physica A Statistical Mechanics & Its Applications, 2003, 328(3):584-606.

[7]Peters K 1. Modelling of cascading effects and efficient response to disaster spreading in complex net-works.[J]. International Journal of Critical Infrastructures, 2008, 4(4):46-62.

[8]翁文國, 倪順江, 申世飛,等. 復雜網絡上災害蔓延動力學研究[J]. 物理學報, 2007, 56(4):1938-1943.

WENG Wenguo, NI Shunjiang, SHEN Shifei,et al. Dynamics of disaster spreading in complex networks[J]. Acta Physica Sinica, 2007, 56(4):1938-1943.

[9]李澤荃, 張瑞新, 楊曌,等. 復雜網絡中心性對災害蔓延的影響[J]. 物理學報, 2012, 61(23):557-563.

LI Zequan, ZHANG Ruixin, YANG Zhao, et al. Influence complex network centrality on disaster spreading[J]. Acta Physica Sinica, 2012, 61(23):557-563.

[10]Schuur E A G, Bockheim J, Canadell J G, et al. Vulnerability of Permafrost Carbon to Climate Change: Implications for the Global Carbon Cycle[J]. BioScience, 2008, 58(8):701-714.

[11]Geneiatakis D, Dagiuklas T, Kambourakis G, et al. Survey of security vulnerabilities in session initiation protocol[J]. IEEE Communications Surveys & Tutorials, 2006, 8(3):68-81.

[12]Gallopín G C. Linkages between vulnerability, resilience, and adaptive capacity[J]. Global Environmental Change, 2006, 16(3):293-303.

[13]汪送, 戰仁軍. 節點免疫力對事故網絡風險傳遞行為的影響分析[J]. 安全與環境工程, 2015, 22(1):126-130.

WANG Song, ZHAN Renjun. Impact analysis of node immunity on risk transfer behavior in accident network[J]. Safety and Environmental Engineering, 2015, 22(1):126-130.

[14]許葭, 宋守信, 袁朋偉,等. 基于ANP的地鐵站點網絡脆弱性評價[J]. 中國安全科學學報, 2015, 25(12):129-134.

XU Jia, SONG Shouxin, YUAN Pengwei, et al. Evaluation of network vulnerability of subway stations based on ANP[J]. China Safety Science Journal, 2015, 25(12):129-134.