模塊化多電平換流器2N＋1電平調制方式研究

譚風雷

（國網江蘇省電力公司檢修分公司，江蘇南京211102）

模塊化多電平換流器2N＋1電平調制方式研究

譚風雷

（國網江蘇省電力公司檢修分公司，江蘇南京211102）

文中研究了一種模塊化多電平換流器2N＋1電平調制方式。分析了N＋1電平調制方式，在充分理解模塊化多電平換流器工作原理的基礎上，推導了2N＋1電平調制方式的實現原理，并分奇、偶2種情況分別給出了具體的實現過程。仿真結果表明，相比于N＋1電平調制方式，2N＋1電平調制方式可以實現2N＋1電平輸出，波形電平數多，諧波含量低，但需要以增加橋臂環流和電感壓降為代價，最后驗證了該方法的可行性和有效性。

模塊化多電平換流器；N＋1電平；2N＋1電平；仿真

0 引言

隨著多電平技術的快速發展，模塊化多電平換流器憑借其拓撲結構帶來的優點［1－4］，深受專家學者們的青睞。其優點主要有高度模塊化設計，集成度高，擴展方便，易于冗余設計；三相橋臂與直流母線側電容器并聯，利于能量的雙向流動；輸出波形質量隨著子模塊數量的增加會不斷提高且易于控制。為了保證模塊化多電平換流器直流母線電壓均勻分配到各個子模塊上，傳統的控制技術［5－8］一般采用N＋1電平調制方式，該方式輸出電壓為N＋1電平，橋臂環流小，電感壓降小。文獻［9］基于H橋級聯多電平的調制原理，提出了2N＋1電平調制方式，并通過仿真實驗驗證了該方法的可行性。該調制方法可以實現2N＋1電平電壓輸出，提高了輸出波形的質量，但帶來了橋臂環流和電感壓降較大的問題。實際上，目前針對模塊化多電平換流器2N＋1電平調制方法的研究不多，很少給出算法的具體實現過程，不夠嚴謹，且不同文獻關于2N＋1電平的調制方法也不同。

基于上述分析，本文通過研究、對比大量相關參考文獻，得到一種模塊化多電平換流器2N＋1電平調制方式，分奇、偶2種情況分別進行討論，主要在于移相方式上不同。仿真實驗驗證了2N＋1電平調制方式的正確性，并與N＋1電平調制方式進行對比。該調制方式輸出波形質量好，但橋臂環流和電感壓降較大。

1 模塊化多電平換流器拓撲結構

模塊化多電平換流器拓撲結構如圖1所示。其由6個橋臂構成，每個橋臂有N個子模塊，假設直流側總壓為Udc，橋臂電感為Ls。介紹模塊化多電平換流器工作原理的文獻［10］較多，就不再贅述。

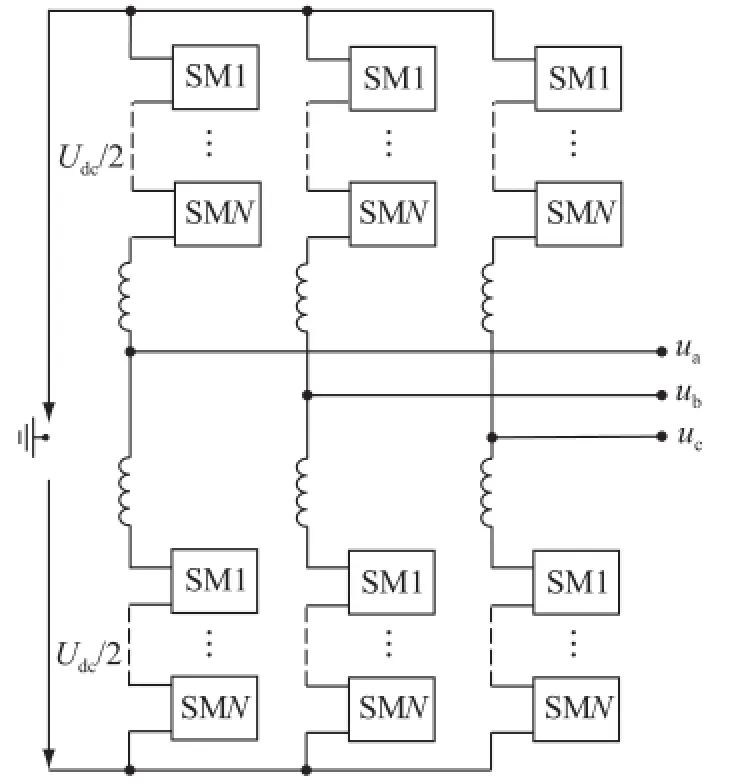
圖1 模塊化多電平換流器拓撲結構Fig.1 Circuit configuration of MMC

2 N＋1電平調制方式

根據參考文獻［11］可知：模塊化多電平換流器中為了保證能量的均壓分配，上、下橋臂電壓之和應為直流側電容電壓，極端情況下如果上橋臂電壓為零，則下橋臂電壓為直流母線側電容電壓Udc，該電壓Udc均壓分配到N個子模塊中，所以子模塊電容電壓為Udc／N。這樣只需要上、下橋臂投入的子模塊數量之和為N，即可保證上、下橋臂電壓之和為直流側電容電壓。這時通過改變上、下橋臂投入的子模塊數量，即可改變輸出電壓。上、下橋臂投入的子模塊數量之和為N存在N＋1種情況，從而可以輸出N＋1種電平。

為了保證上、下橋臂投入的子模塊數量之和為N，當上橋臂投入一個子模塊時，對應的下橋臂應該切除一個子模塊，即上、下橋臂對應的子模塊的驅動信號相反。為保證驅動信號相反，只需將參考電壓信號和三角載波信號同時取反即可。

總結模塊化多電平換流器開關通斷的特點，結合載波移相技術，文獻［10］給出了基于載波移相技術的N＋1電平調制方式。針對上橋臂，將參考電壓信號取反后作為調制信號，將幅值、頻率相同，相位相差360°／N，最大值為1，最小值為0的三角波作為載波；針對下橋臂，將參考電壓信號作為調制信號，將幅值、頻率相同，相位相差360°／N，最大值為1，最小值為0的三角波分別移相180°后作為載波。

為了更加直觀地體現N＋1電平調制方式，以N＝2和N＝3為例，分別給出了上、下橋臂調制信號和載波信號，如表1和表2所示，其中Uref為實際參考電壓信號。

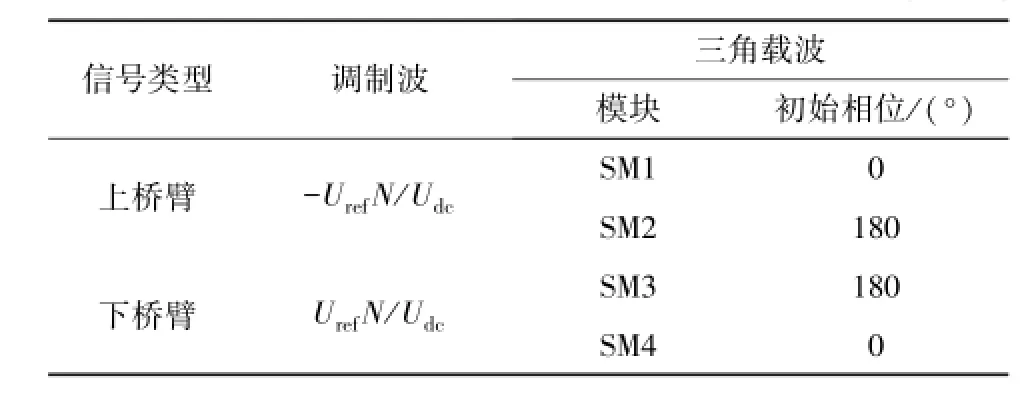
表1 模塊化多電平換流器N＋1電平調制方式（N＝2）Table 1 Modulation method for N＋1 levels of MMC（N＝2）

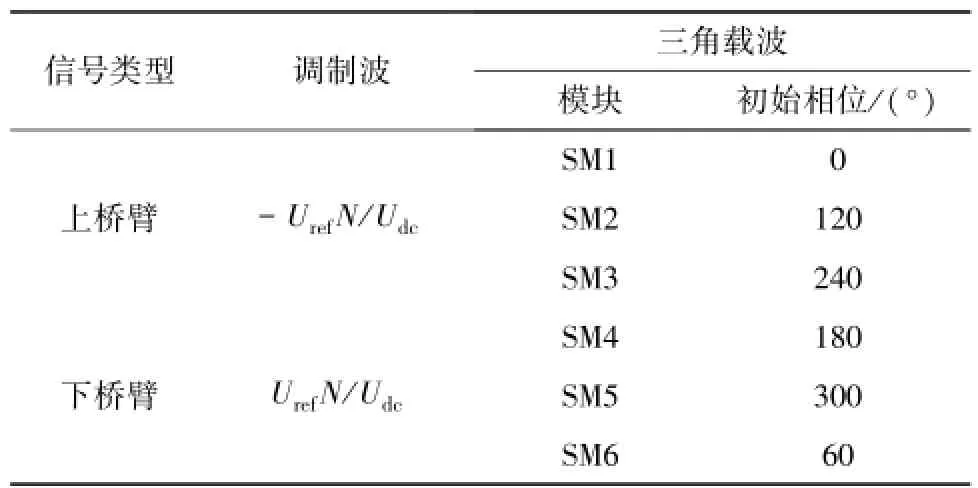
表2 模塊化多電平換流器N＋1電平調制方式（N＝3）Table 2 Modulation method for N＋1 levels of MMC（N＝3）

3 2N＋1電平調制方式

H橋級聯型多電平換流器中采用180°／N移相方式，N個子模塊可以輸出2N＋1電平，對比于2N個子模塊的模塊化多電平換流器理論上依然可以輸出2N＋1電平，這樣可以極大增加電平數，減少諧波含量，提高波形質量，同時在保證電平數相同時，可以有效減少子模塊數量，進一步降低成本。

基于以上分析，文獻［12］考慮將180°／N移相方式應用到模塊化多電平換流器中，并給出了詳細的分析。為了使模塊化多電平換流器輸出2N＋1電平，這時就無法保證上、下橋臂投入的子模塊數量之和為N，即：

式中：np為上橋臂需要投入的子模塊數量；nn為下橋臂需要投入的子模塊數量。

當上、下橋臂投入的子模塊數量之和不為N時，為了保證直流母線側電容電壓的穩定，這時橋臂電感上會承擔較大壓降，因此不能將其忽略［9］，則考慮電感壓降后輸出電壓ux（x＝a，b，c）可以表示為：

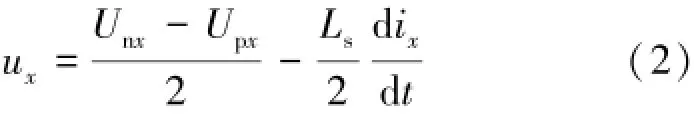
式中：Upx為x相上橋臂的電壓；Unx為x相下橋臂的電壓。將np和nn代入式（2）可得：

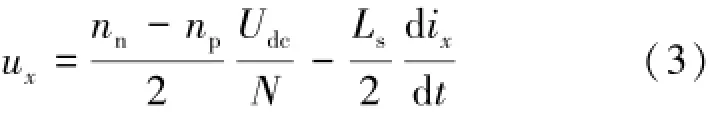
將np＋nn＝N代入式（3）可得：

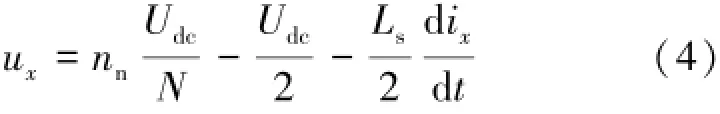
式中：nn∈［0，N］。由式（4）可知，輸出電壓ux為N＋1電平。為了使ux為2N＋1電平，假設np＋nn＝N＋1，則式（4）為：

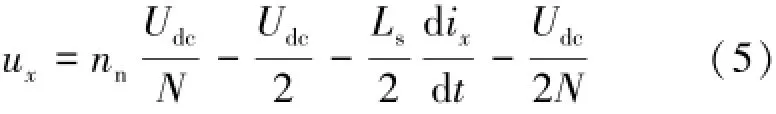
此時nn∈［1，N］。由式（5）可知，輸出電壓ux為N電平，與式（4）中的N＋1電平輸出電壓ux不同，進而現實了2N＋1電平輸出，同理可以假設np＋nn＝N－1，則式（4）為：

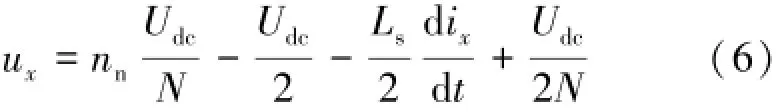
上述分析表明，輸出電壓ux同樣可以達到2N＋1電平。綜上所述，模塊化多電平換流器要想實現2N＋1電平輸出，上、下橋臂投入子模塊數量之和不為定值，必須滿足以下條件：

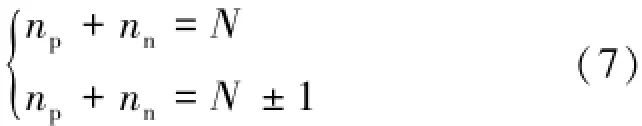
當輸出電壓ux為2N＋1電平時，由于輸出電流在上、下橋臂電感上的壓降之和為0，故只考慮環流作用在單個電感上的壓降uZLx，可表示為：

顯然，當上、下橋臂投入的子模塊數量之和為N時，uZLx為0，橋臂環流很小幾乎可以忽略；但當上、下橋臂投入的子模塊數量之和不為N時，uZLx為｜Udc／2N｜，即子模塊電容電壓的一半，這時環流較大不能忽略。

前面分析了模塊化多電平換流器實現2N＋1電平輸出的原理［13－16］，下面將詳細給出具體的調制方式。實際上，要實現2N＋1電平輸出，子模塊數量N的奇偶也是十分重要的，奇偶性不同，三角載波相位不同［9］。當子模塊數量N為奇數時，將參考電壓信號作為下橋臂的調制信號，該調制信號取反后作為上橋臂的調制信號，將幅值、頻率相同，相位相差360°／N，最大值為1，最小值為0的三角波作為上橋臂的載波，而下橋臂載波與上橋臂載波完全相同；當子模塊數量N為偶數時，上、下橋臂調制信號與N為奇數時相同，將幅值、頻率相同，相位相差360°／N，最大值為1，最小值為0的三角波作為上橋臂的載波，將上橋臂載波分別移相180°／N后作為下橋臂載波。以N＝2和N＝3為例進行具體說明，2N＋1電平調制方式如表3、表4所示。

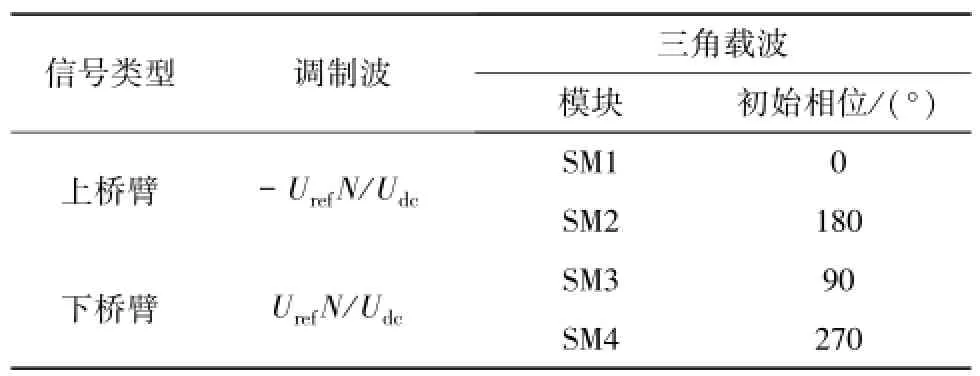
表3 模塊化多電平換流器2N＋1電平調制方式（N＝2）Table 3 Modulation method for 2N＋1 levels of MMC（N＝2）

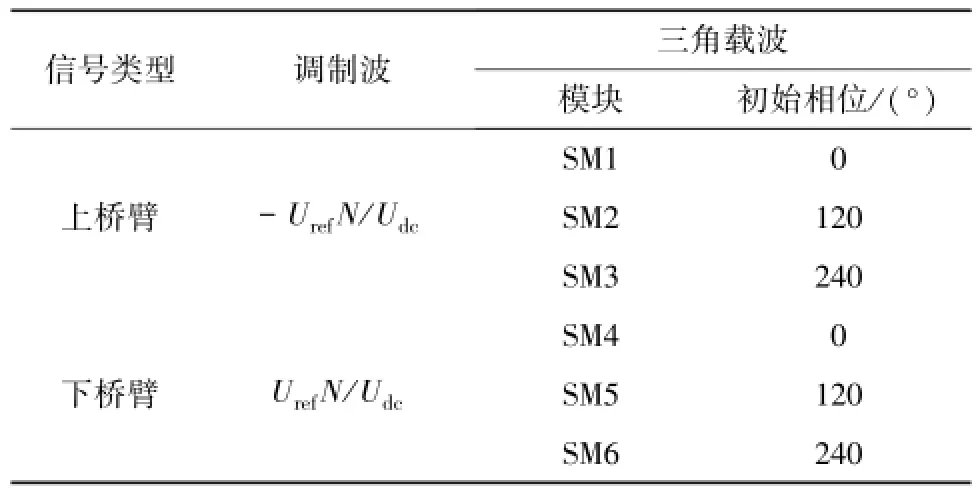
表4 模塊化多電平換流器2N＋1電平調制方式（N＝3）Table 4 Modulation method for 2N＋1 levels of MMC（N＝3）

4 仿真研究

為了驗證模塊化多電平換流器N＋1電平調制方式與2N＋1電平調制方式的可行性和有效性，在PSCAD軟件中搭建了仿真模型，該模型采用三相模塊化多電平逆變器，主要參數如表5所示。

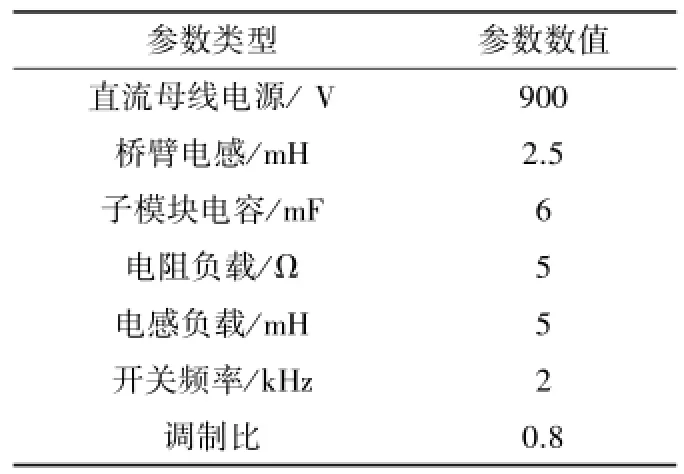
表5 仿真模型中主要參數Table 5 Circuit parameters

當N為奇數時，以N＝3為例進行分析說明，仿真結果如圖2、圖3所示。比較圖2（a）、圖2（b）與圖3（a）、圖3（b）可知，N＋1電平調制方式輸出波形為四電平，其基波含量為361.6 V，諧波含量（THD）為50.00%，高次諧波主要集中在6 kHz及其倍數次，而2N＋1電平調制方式輸出波形為五電平，其基波含量為359.7 V，THD為23.90%，高次諧波主要集中在12 kHz及其倍數次，顯然2N＋1電平調制方式電平多，輸出波形諧波含量低，質量高，但基波含量相對偏低，控制效果遠優于N＋1電平調制方式。

比較圖2（c）、圖2（d）與圖3（c）、圖3（d）可知，N＋1電平調制方式輸出環流的直流含量為12.61 A，二次諧波含量為3.10 A，幾乎沒有高次以及開關次諧波，而2N＋1電平調制方式輸出環流的直流含量為12.70 A，二次諧波含量為3.32 A，基本與N＋1電平調制方式相同，但其存在3倍的開關次諧波且含量為1.08 A，因此2N＋1電平調制方式盡管可以實現2N＋1電平輸出，但是需要以增加環流為代價。

比較圖2（e）、圖2（f）與圖3（e）、圖3（f）可知，N＋1電平調制方式的橋臂電感壓降（忽略基波電壓分量）中主要含有6 kHz諧波17.34 V以及12 kHz諧波5.40 V，與理論結果不同，但考慮到忽略了開關過程，仿真結果與理論結果存在一定差異也是正常的。而2N＋1電平調制方式的橋臂電感壓降中主要含6 kHz諧波84.35 V以及18 kHz諧波18.88 V，由式（8）可知，橋臂電感壓降幅值最大值應為150 V（Udc／2N），但由于采用2N＋1電平調制方式，橋臂電感壓降幅值應該在0與150 V之間以3倍開關頻率6 kHz變化，所以橋臂電感壓降等效幅值應該小于150 V，而84.35 V滿足要求，進而也驗證了式（8）的正確性。當N為偶數時，其分析過程與N為奇數時完全一樣。

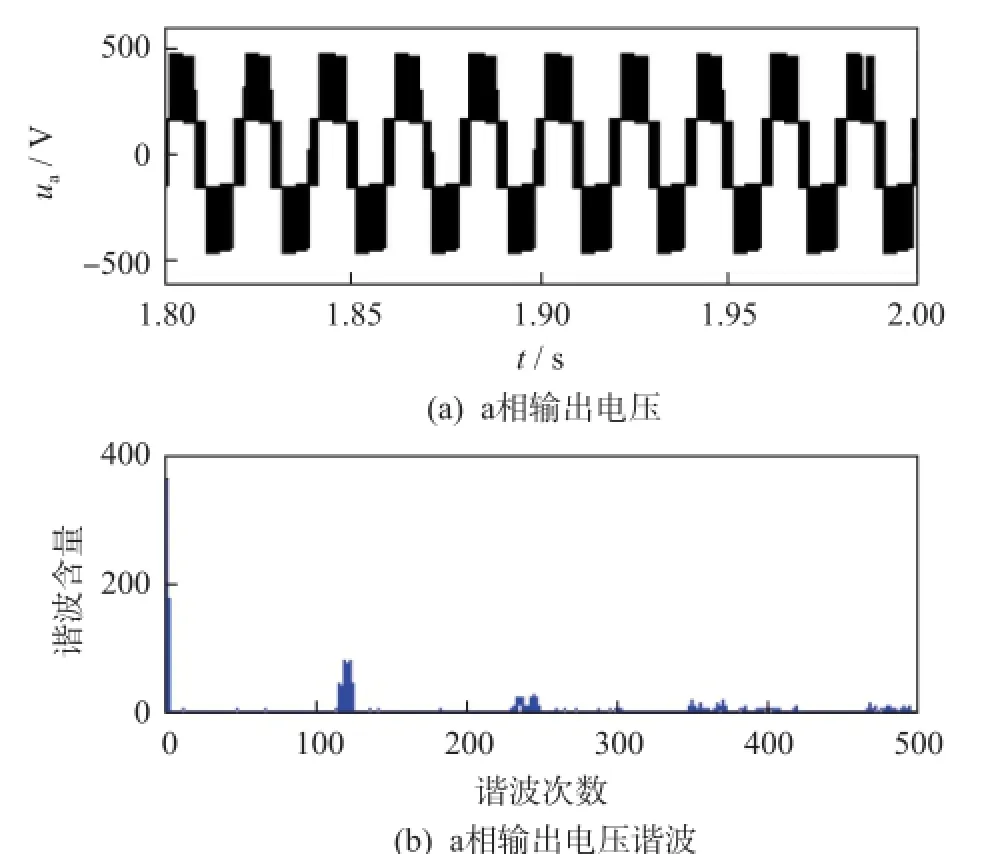
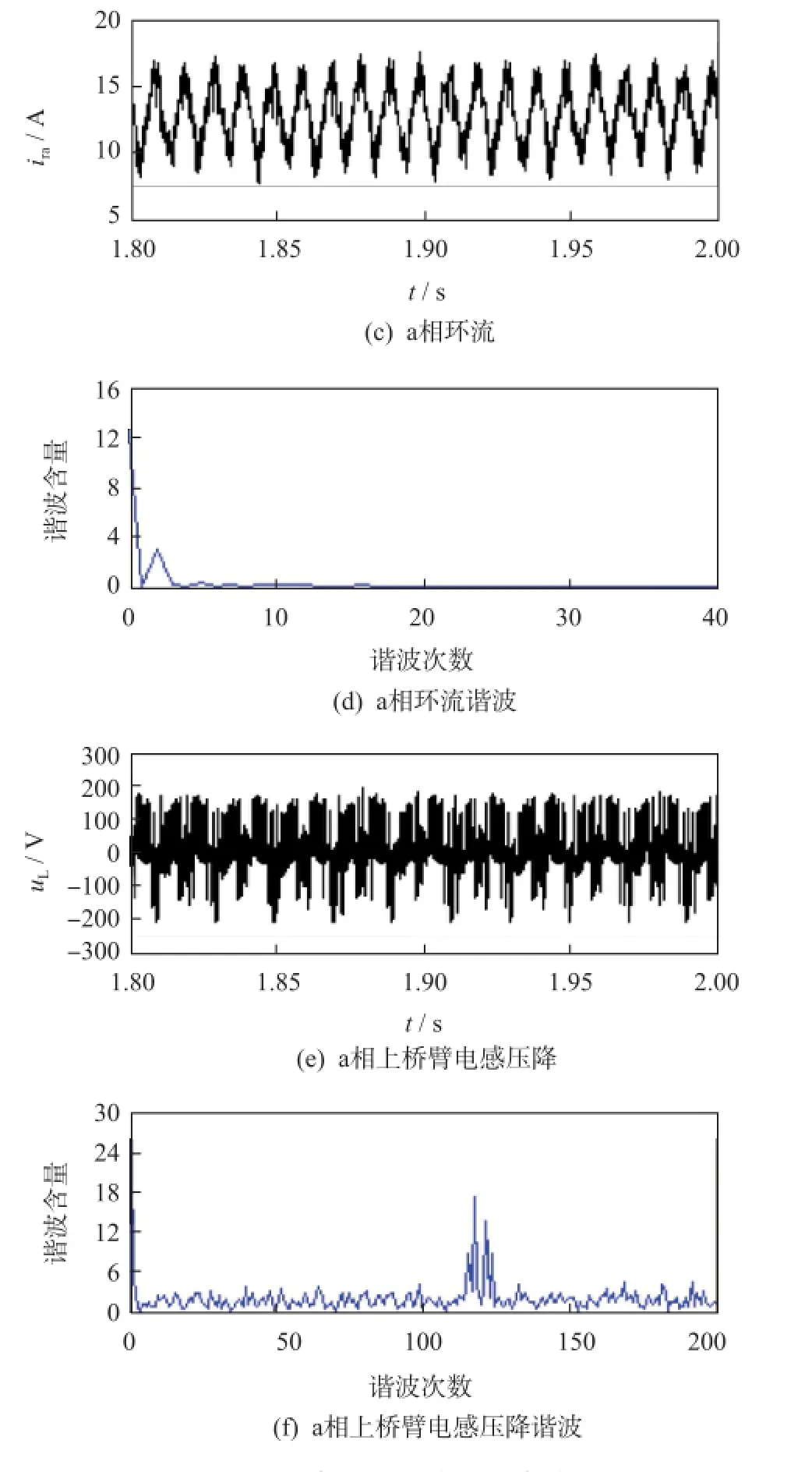
圖2 N＋1電平調制方式仿真波形Fig.2 Simulation waveforms of Modulation method for N＋1

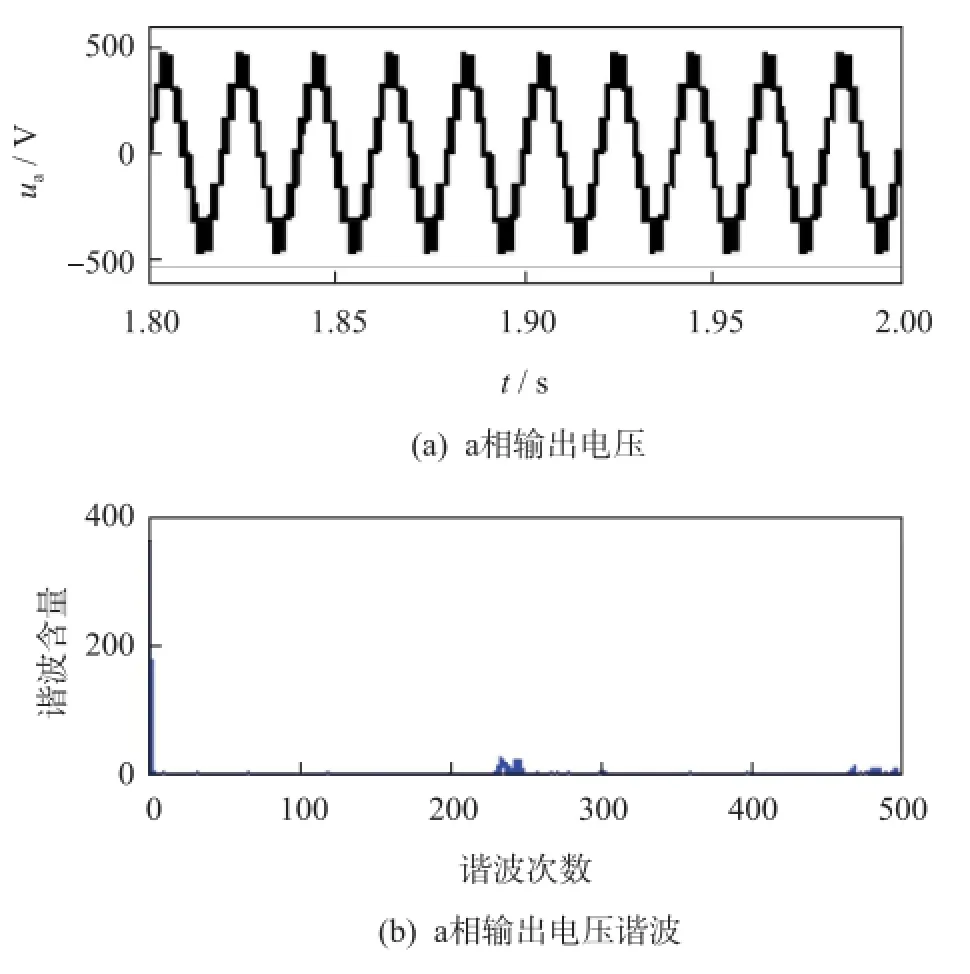
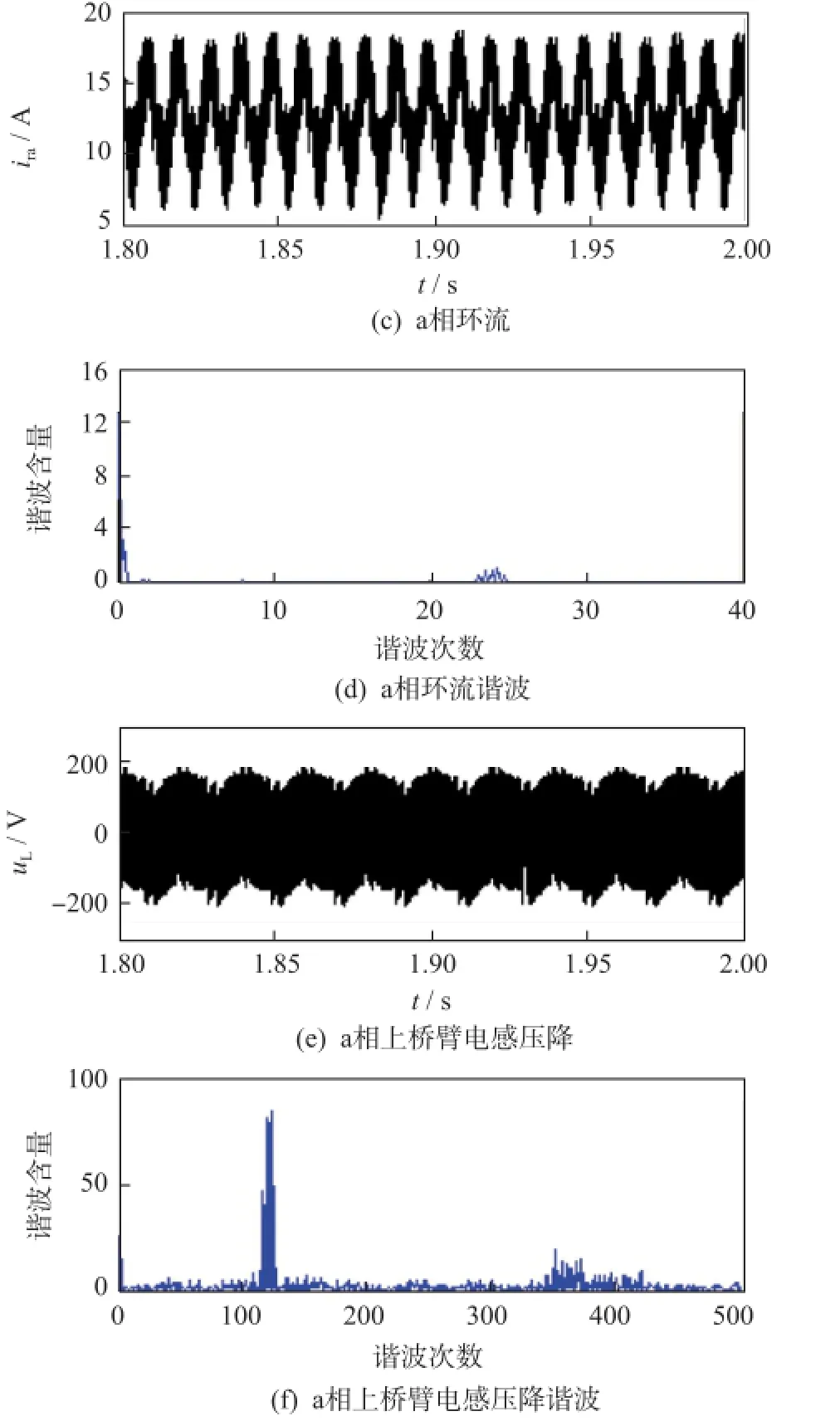
圖3 2N＋1電平調制方式仿真波形Fig.3 Simulation waveforms of Modulation method for 2N＋1

綜上所述，N＋1電平調制方式輸出電壓為N＋1電平，高次諧波主要集中在N fk及其倍數次，其環流主要含有直流分量和二次諧波分量，而橋臂電感壓降較小且主要集中在N fk及其倍數次。與其對應的2N＋1電平調制方式輸出電壓為2N＋1電平，高次諧波主要集中在2N fk及其倍數次，其環流不僅含有直流分量和二次諧波分量，且存在較大的N fk諧波分量，而橋臂電感壓降較大，一般略小于Udc／2N，且主要集中在N fk及其倍數次。相對于N＋1電平調制方式，2N＋1電平調制方式輸出波形質量高，但其需要以增加環流和橋臂電感壓降為代價。

5 結語

在充分理解模塊化多電平換流器拓撲結構的基礎上，詳細給出了N＋1電平調制方式的實現過程。推導了2N＋1電平調制方式的實現原理，并分奇、偶2種情況，分別給出了各自具體的實現過程。利用PSCAD仿真模型驗證了2種調制方式的正確性，得出以下結論：2N＋1電平調制方式相對N＋1電平調制方式而言，其輸出波形質量高，但需要以增加環流和橋臂電感壓降為代價。

［1］王寶安，譚風雷，商 姣.模塊化多電平換流器模塊冗余優化配置方法［J］.電力自動化設備，2015，35（1）：13－19.

WANG Baoan，TAN Fenglei，SHAO Jiao.Optimal configuration of modular redundancy for MMC［J］.Electric Power Automation Equipment，2015，35（1）：13－19.

［2］胡兆慶，董云龍，田 杰，等.基于模塊化多電平換流器結構的柔性直流控制策略［J］.江蘇電機工程，2013，32（1）：5－9.

HU Zhaoqing，DONG Yunlong，TIAN Jie，et al.Control strategy research of VSC－HVDC based on modular multilevel converter［J］.Jiangsu Electrical Engineering，2013，32（1）：5－9.

［3］季振東，趙劍鋒.模塊化多電平技術在電力系統中的應用前景分析［J］.江蘇電機工程，2015，34（6）：41－45.

JI Zhendong，ZHAO Jianfeng.Prospect analysis of modular multilevel technology in power system［J］.Jiangsu Electrical Engineering，2015，34（6）：41－45.

［4］林子杰，劉建坤，陳 靜，等.基于粒子群算法的MMCUPFC參數優化［J］.江蘇電機工程，2015，34（6）：23－27.

LIN Zijie，LIU Jiankun，CHEN Jing，et al.A PSO algorithm based approach for optimizing MMC－UPFC control system pa?rameters［J］.Jiangsu Electrical Engineering，2015，34（6）：23－27.

［5］王姍姍，周孝信，湯廣福，等.模塊化多電平電壓源換流器的數學模型［J］.中國電機工程學報，2011，31（24）：1－8.

WANG Shanshan，ZHOU Xiaoxin，TANG Guangfu，et al.Mod?eling of modular multi?level voltage source converter［J］.Pro?ceedings of the CSEE，2011，31（24）：1－8.

［6］周月賓，江道灼，郭 捷，等.模塊化多電平換流器子模塊電容電壓波動與內部環流分析［J］.中國電機工程學報，2012，32（24）：8－14.

ZHOU Yuebin，JIANG Daozhuo，GUO Jie，et al.Capacitive voltage fluctuation and internal circulation analysis of modular multilevel converter sub?module［J］.Proceedings of the CSEE，2012，32（24）：8－14.

［7］HAGIWARA M，AKAGI H.Control and experiment of pulse width?modulated modular multilevel converters［J］.IEEE Trans?actions on Power Electronics，2009，24（7）：1737－1746.

［8］SHE X，HUANG A，NI X，et al.AC circulating currents sup?pression in modular multilevel converter［C］.IECON 2012－38th Annual Conference on IEEE Industrial Electronics Society. Montreal，QC，IEEE，2012：191－196.

［9］王思藴.模塊化多電平變流器控制方法的研究［D］.杭州：浙江大學，2013.

WANG Siyun.Research on control method of modular multilevel converter［D］.Hangzhou：Zhejiang University，2013.

［10］商 姣.基于模塊化的的高壓變頻裝置研究［D］.南京：東南大學，2013.

SHANG Jiao.The study on high?voltage inverter based on modular multilevel converter［D］.Nanjing：Southeast Univer?sity，2013.

［11］王 靚，任洪強，陳國宇，等.基于MMC的三相四線制電能質量補償裝置［J］.江蘇電機工程，2016，35（1）：57－61.

WANG Liang，REN Hongqiang，CHEN Guoyu，et al.A com?pensation device of power quality in three?phase four?wire sys?tem based on modular multi?level inverter［J］.Jiangsu Electrical Engineering，2016，35（1）：57－61.

［12］譚風雷.基于MMC的電機拖動系統控制策略研究［D］.南京：東南大學，2015.

TAN Fenglei.Research on the control strategy of motor drive system based on modular multilevel converter［D］.Nanjing：Southeast University，2015.

［13］饒 宏，李建國，宋 強，等.模塊化多電平換流器直流輸電系統損耗的計算方法及其損耗特性分析［J］.電力自動化設備，2014，34（6）：101－106.

RAO Hong，LI Jianguo，SONG Qiang，et al.Losscalculation method and characteristics analysis for MMC－HVDC system［J］.Electric Power Automation Equipment，2014，34（6）：101－106.

［14］蔡新紅，趙成勇.模塊化多電平換流器型高壓直流輸電系統控制保護體系框架［J］.電力自動化設備，2013，33（9）：157－163.

CAI Xinhong，ZHAO Chengyong.Framework of control and protection system for MMC－HVDC transmission system［J］. Electric Power Automation Equipment，2013，33（9）：157－163.

［15］張振華，江道灼.基于模塊化多電平變流器的STATCOM研究［J］.電力自動化設備，2012，32（2）：62－66.

ZHANG Zhenhua，JIANG Daozhuo.STATCOM based on modularized multilevel converters［J］.Electric Power Automa?tion Equipment，2012，32（2）：62－66.

［16］李 強，賀之淵，湯廣福，等.新型模塊化多電平換流器空間矢量脈寬調制的通用算法［J］.電網技術，2011，35（5）：59－64.

LI Qiang，HE Zhiyuan，TANG Guangfu，et al.A generalized algorithm of space?vector PWM for a new type of modular mul?tilevel converter［J］.Power System Technology，2011，35（5）：59－64.

Research on 2N＋1 Level Modulation Method of Modular Multilevel Converter

TAN Fenglei
（State Grid Jiangsu Electric Power Maintenance Branch Company，Nanjing 211102，China）

A 2N＋1 level modulation method of modular multilevel converter（MMC）is studied in this paper.The N＋1 level modulation is analyzed.The realization principle of 2N＋1 level modulation method is deduced on the basis of fully understanding the working principle of MMC，and the specific implementation process is given according to the situation of odd and even.Simulation results show that comparing with the N＋1 level modulation mode，2N＋1 level modulation mode can achieve 2N＋1 level output with more waveform levels and low harmonic content，but the cost is the increase of bridge arm circulation and inductance drop.The feasibility and validity of the 2N＋1 level modulation method are verified.

modular multilevel converter；N＋1 level；2N＋1 level；simulation

TM531

：A

：2096－3203（2017）02－0099－05

譚風雷

譚風雷（1989—），男，重慶萬州人，碩士，從事特高壓電網變電運行維護的工作。

（編輯 劉曉燕）

2016－11－19；

2016－12－30