特殊工況下基于三角形計算的高精度輸電線路單端測距方法

馮 暢，李 峰，宋 爽，陸 帥，王 可

（1.南京磐能電力科技股份有限公司，江蘇南京210031；2.國網江蘇省電力公司電力科學研究院，江蘇南京211103）

特殊工況下基于三角形計算的高精度輸電線路單端測距方法

馮 暢1，李 峰1，宋 爽2，陸 帥1，王 可1

（1.南京磐能電力科技股份有限公司，江蘇南京210031；2.國網江蘇省電力公司電力科學研究院，江蘇南京211103）

準確的故障測距是輸電線路故障后快速恢復供電的重要前提。一般來說，線路上發生單相接地故障時，因過渡電阻的影響，導致計算阻抗無法正確反映保護安裝處至故障點的線路阻抗值，必須借助雙端測距才可獲得精確測距值。文中在分析附加阻抗來源的基礎上，提出在特殊的工況下，雙端測距失效，基于三角形計算的單端測距可精確測距，并且此方法可以推廣至架空線、地纜混合參數的輸電線路故障。經過仿真數據以及現場數據驗證，該方法具有較高的精度。

單端測距；雙端測距；阻抗計算；混合參數輸電線路；T接線

0 引言

輸電線路的故障測距是一個橫亙在繼電保護工程師面前的經典問題［1，2］，精確的故障測距對于縮減巡線時間，快速恢復供電具有極其重要的意義［3－5］。國內110 kV及其以上的輸電線路多安裝有含距離保護功能的保護裝置，依托于距離保護阻抗計算功能的單端故障測距功能可以在保護動作后迅速地給出測距結果，給現場工作人員以較直觀的故障位置提示，因此廣受現場的歡迎。但是這種基于單端阻抗計算的測距方法也具有較強的局限性，對于線路上發生的多相故障，因相間阻抗一般是弧光電阻，其值較小［6，7］，一般來說精度還算理想；但是對于線路上發生單相經過渡電阻接地的故障，因過渡電阻阻值不確定［8］，并且對于雙端供電線路，由于對側電源的助增作用，往往導致計算阻抗無法正確反映保護安裝處至故障點的線路阻抗值［9］，從而無法給出有參考價值的測距結果。

文章在分析基于單端阻抗法測距的原理基礎上，提出在某些特殊的工況下，單端阻抗法也可以精確地給出測距值。進而將這種方法推廣至架空線、地纜混合參數的輸電線路故障。經過仿真數據以及現場數據驗證，該方法具有較高的精度。

1 測距方法

1.1阻抗測距原理

保護裝置一般來說采集其固定安裝處的電流、電壓信息，輸電線路上的故障位置隨機不可預見，但保護安裝處電流、電壓值與線路故障發生處電流、電壓值滿足一定的約束條件。由序分量法可知，在輸電線路上發生不對稱故障時，電力系統可以分解為正序、負序、零序3個序網絡，因各序網絡的拓撲結構、元件參數各有不同，所以3個序網絡必須獨立分析，如圖1所示。

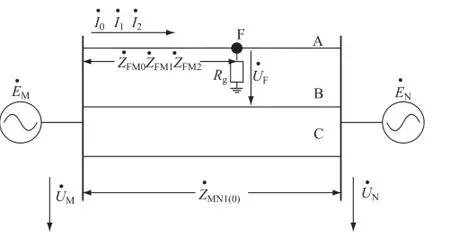
圖1 系統結構圖Fig.1 System topology

（1）適用于所有類型的不對稱故障。對于兩相短路（以BC兩相短路為例（接地、不接地）），其過渡電阻多為弧光電阻，數值較小，因此有，由式（1）得：

對于單相短路，以A相短路為例，由式（1）得：

1.2單相接地時附加阻抗ΔZ·分析

接地短路時，過渡電阻為純阻性［12］，記為Rg，流入故障點故障電流為根據單相短路時的序網圖可知如圖2所示。

圖2 單相短路的綜合序網圖Fig.2 Synthetical sequence network for single phase fault

M側保護感受到的故障分量正負零序電流是通過并聯電路分流后的電流。同理Δ考慮正序負阻抗相等有。如圖3所示。

圖3 正序故障電流分流圖Fig.3 Positive sequence fault current distribution diagram

根據線性電路的迭加原理，故障后M側保護感受到的電流為故障前負荷電流與故障電流的迭加，設負荷電流為因此：及CM1，CM0，K對于有影響。因故障點電流不可測，致

由式（4）可知未知；因故障點位置未知，致CM1，CM0數值未知。綜上述是一個幅值、相角皆未知的復數。其中對于的影響在送電端、受電端表現地不同。從定性的角度看，在受電端表現為抗性，在送電端表現為容性。如圖4所示。

圖4 單相接地短路的電氣相量圖Fig.4 Electrical vector diagram of single phase fault

假設故障發生于MN的中點處，M側測量到的負荷電流超前于故障點流過的故障電流，ΔZ·表現出容性；相反，在N側表現出抗性。若故障前線路一端開關分開，因值已知，Rg未知，則表現為一個幅值未知、相角已知的復數。

1.3特殊工況下的精確單端測距

由上可知一般情況下單相經過渡電阻短路時，因過渡電阻的存在，導致附加計算阻抗ΔZ·為幅值、相角未知的復數，所以計算阻抗無法準確表示從保護安裝處至故障點的線路阻抗。但在下述幾種情況下，ΔZ·近似表現為相角已知幅值未知的復數。

（1）線路一端送電，手合于故障；

（2）開關三跳后，先發重合令一端重合于故障；

（3）線路一端開關處于合位，另一端處于分位，故障發生。

考慮ΔZ·為相角已知、幅值未知的復數，則阻抗相量圖如圖5所示。

圖5 單相接地短路的阻抗相量圖Fig.5 Impedance vector diagram of single phase fault

隨著架空線、電纜混合參數線路在電網中的大量使用，對于混合參數線路測距的研究具有十分重要的現實意義［13］。上述方法亦可推廣使用于架空線、電纜混合鋪設的輸電線路的單端測距。如圖6所示。

圖6 混合線路參數系統結構圖Fig.6 System topology of a hybrid parameter transmission line

圖6 中，MN之間的輸電線路由不同參數的

首先假設故障發生于MK段，使用式（11）、式（12）進行測距計算，如測距結果0≤ρ≤1.0，則表明測距成功，故障發生于MK段；否則計算K端電壓，再次調用式（11）、式（12）進行測距計算。需要說明的是，電纜線路因其對地導納值不可忽略，因此此時非故障相電流亦非0，測距使用的是流經線路的電流，所以需要扣除對地電容電流的影響。以M側為例，使用公式，計算三序網絡中流經電容的電流合成為相電流側保護安裝處電流互感器感受到的三相電流分別減去即得到流經線路MK的三相電流同理可以獲得流經線路KN的電流。如圖7所示。

圖7 考慮電纜對地電容后的混合線路參數系統結構圖Fig.7 System topology of a hybrid parameter transmissionline with capacitor of cable line considered

2 算例

2.1普通線路算例

2015－03－04 T 14：10，220 kV甲乙線在甲站送電時發生B相接地短路故障，開關三相跳開后不重合，對側乙變斷路器在斷開位置。故障波形如圖8所示。

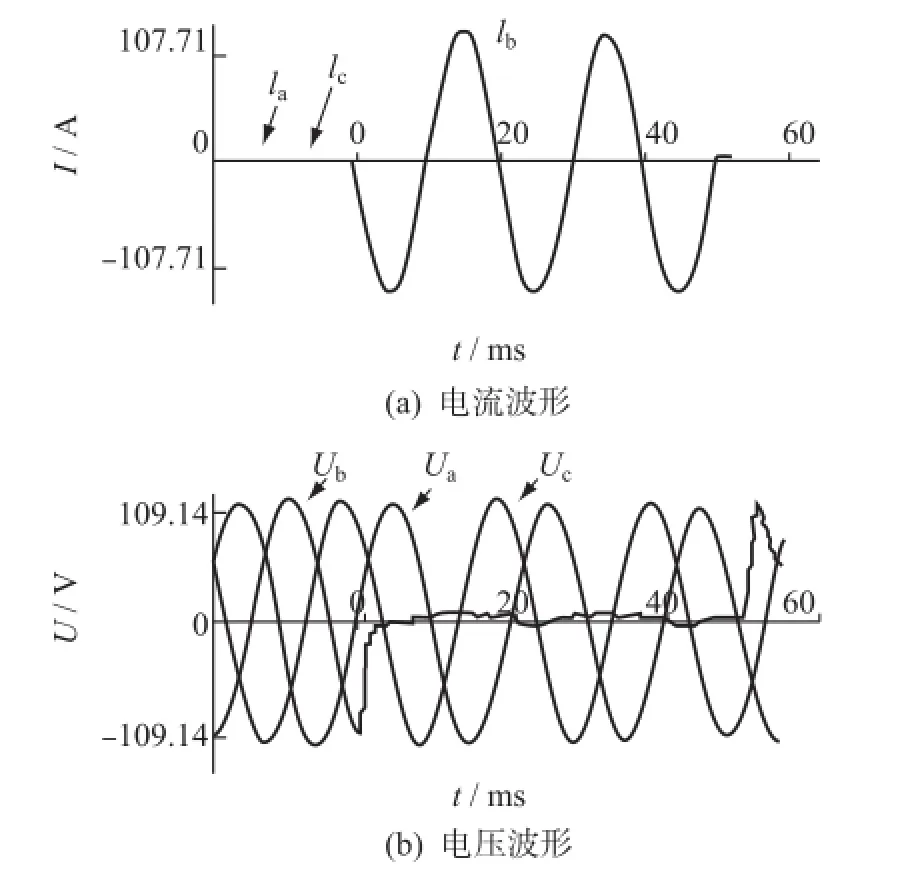
圖8 甲乙線甲側送電合于BG短路Fig.8 Waveform of current and voltage for the fault of AB line delivering power only from station A with a BG fault on the line

線路一次參數：R1＝0.013 Ω，X1＝0.158 Ω；R0＝0.051 Ω，X0＝0.42 Ω，線路全長L＝1.5 km；TV變比為220 kV／100 V，TA變比為2500 A／5 A。取故障后20～40 ms的數據進行全波傅里葉變換，獲取的相量數據為：

將獲取的相量數據代入式（11）、式（12）計算得ρ＝0.592，折算至有名值為0.898 km。巡線得知實際故障點距離甲站0.85 km。

2.2混合參數線路算例

使用PSCAD建立如圖7所示的500 kV電力系統模型，其中MK為電纜線路，其一次參數R1＝0.45 Ω，X1＝5.969 Ω，XC1＝33 500 Ω；R0＝3.9 Ω，X0＝18.35 Ω，XC0＝502 500 Ω；線路長L＝50 km。KN為架空線路，其一次參數R1＝1.170 5 Ω，X1＝13.345 Ω，XC1＝4 025 600 Ω；R0＝9.055 Ω，X0＝34.19 Ω，XC0＝7 095 600 Ω，線路長L＝50 km。KN線路上距K點25 km處發生經50 Ω的AG短路。故障波形如圖9所示。

取故障后20～40 ms的數據進行全波傅里葉變換，獲取的相量數據為：假設故障在MK段，計算得ρ＝2.02，假設故障在KN段，計算得ρ＝0.488。

圖9 混合參數線路M側送電合于AG短路Fig.9 Waveform of current and voltage for the fault of a hybrid parameter transmission line delivering power only from station M with a AG fault on the line

3 分析與討論

（1）在本文描述的工況下，線路開關開斷側因未感受到故障電流、電壓，所以此時雙端測距方法失效。

（2）對于故障前重載負荷并且經較大過渡電阻接地的單相短路，因負荷電流相比于故障電流不可忽略，因此轉換成電阻電抗型或者電阻電容型，且的幅值、相角皆未知，無法準確測距。如故障前線路空載或輕載，負荷電流相比于故障電流可以忽略不計，若線路的正序阻抗角與零序阻抗角相差

不大，可假設CM1，CM0，K皆為實數，為實數，即相角為0。啟用本文述方法，或有一定誤差，但可提供一個有一定參考價值的單端測距結果。

（3）精確使用本文所提方法的前提條件是，單相短路且線路一端開關處于分位。交互線路兩端的開關位置狀態信息是必要條件，光纖縱差保護可以交互線路兩端的模擬量、開關量［15］，為使用本方法提供了物質保證。對于普通距離保護，如手合于故障，可斷定對側開關處于分位，可精確使用本方法。

（4）對于故障前有載并經較大過渡電阻接地的單相短路，雖然線路保護第一次跳閘時本文所示方法不適用，但若保護裝置投有三相重合閘方式，并且合于永久故障，那么先合閘那側的保護裝置依然可使用本方法測距，并且得出較為精確的測距結果。

（5）單相經高阻接地短路時，距離保護有可能無法動作，由零序保護動作［16］。但從上文的分析可知，不影響本文所述方法的使用。

（7）對于T接線路的故障測距，需計算獲得故障支路和故障點位置2個信息［17］。T接點至電源之間的輸電線路的參數可不同，仿前文混合參數線路故障測距方法，特殊工況下利用單端數據可計算T接線路的故障測距信息。如圖10所示，若計算的故障支路為MT，則其為惟一測距結果；否則故障支路可能為NT或ST，本方法可給出2個可能的測距結果。雖不惟一，但亦可給巡線工作帶來一定參考意義。

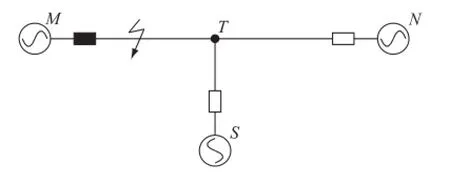
圖10 特殊工況下T接線路故障的系統接線Fig.10 Diagrammatic sketch of fault on a TEED line under special working conditions

4 結語

輸電線路上發生經過渡電阻的單相接地短路時，過渡電阻Rg轉換為未知相量ΔZ·，從而導致傳統基于計算阻抗的單端測距方法有較大誤差。本文論述了在特殊工況下，在由母線至故障點阻抗、計算阻抗過渡電阻附加阻抗3個相量構成的三角形中，三角形的3個角已知，一邊長度已知因此可利用三角形正弦定理求得進而獲取故障測距值。

基于三角形計算的單端測距方法物理概念明確，計算簡單，易于實現，具有較強的精度與實用性，并且已被仿真數據以及現場數據所驗證。

［1］黃建新，李國棟，吳薛紅，等.電力傳輸線路單端故障測距新算法［J］.江蘇電機工程，2003，22（1）：19－20.

HUANG Jianxin，LI Guodong，WU Xuehong，et al.A new al?gortihm of single?terminal fault distance measurement of trasmis?sion line［J］.Jiangsu Electrical Engineering，2003，22（1）：19－20.

［2］吳浩然，李 澄.采用不同步數據的故障測距新原理研究［J］.江蘇電機工程，2016，35（6）：73－76.

WU Haoran，LI Cheng.Research on novel fault location princi?ple with asynchronous data［J］.Jiangsu Electrical Engineering，2016，35（6）：73－76.

［3］葛耀中.新型繼電保護和故障測距的原理與技術［M］.2版.西安：西安交通大學出版社，2007：256－335.

GE Yaozhong.Principles and techniques of new type relay and fault location［M］.2nd ed.Xi an：Xi an Jiaotong University Press，2007：256－335.

［4］洪佩孫，李九虎.輸電線路距離保護［M］.北京：中國水利電力出版社，2008：216－236.

HONG Peisun，LI Jiuhu.Distance relay protection for transmis?sion lines［M］.Beijing：China Water＆Power Press，2008：216－236.

［5］SAHA M M，LZYKOWSKI J，ROSOLOWSKI E.Fault location on power networks［M］.London：Springer?Verlag，2010：1－25.

［6］ANDRICHAK J G.ALEXANDER G E.Distance relays funda?mentals［EB／OL］.GE Power Management，General Electric Co.Malvern，PA，GER?3966.http：∥store.gedigitalenergy. com／faq／documents／alps／ger?3966.pdf.

［7］WILKINSON S B，MATHEWS C A.Dynamic characteristics of mho distancerelays［EB／OL］，GEPowerManagement，General Electric Co.Malvern，PA，GER?3742.http：∥store. gedigitalenergy.com／faq／Documents／Alps／GER?3742.pdf.

［8］LEWIS J.BLACKBURN.Symmetrical components for power systems engineering［M］.first edition.Boca Raton：CRC Press，1993：1－5.

［9］LEWIS J.BLACKBURN，DOMIN T J.Protective relaying：principles and applications［M］.Boca Raton：CRC Press，2006：410－474.

［10］賀家李，李永麗，董新洲，等.電力系統繼電保護原理［M］. 4版.北京：中國電力出版社，2010：98－164.

HE Jali，LI Yongli，DONG Xinzhou，et al.Principles of pro?tective relays for power system［M］.4th ed.Beijing：China Electric Power Press，2010：98－164.

［11］張保會，尹相根.電力系統繼電保護［M］.北京：中國電力出版社，2005：67－125.

ZHANG Baohui，YIN Xianggen.Protective relays for power system［M］.Beijing：China Electric Power Press，2005：67－125.

［12］施世鴻，何奔騰.不受TA飽和影響的高壓輸電線路故障測距算法［J］.電力系統自動化，2008，32（2）：67－70.

SHI Shihong，HE Benteng.Fault location algorithm for HV transmission lines lmmune to saturation of current transformers［J］.Automation of Electric Power system，2008，32（2）：67－70.

［13］吳承恩，邰能靈，郁惟鏞，等.超高壓電纜—架空線混合線路故障測尋方法［J］.電力系統自動化，2005，29（10）：26－29.

WU Chengen，TAI Nengling，YU Weiyong.New method of fault detection and location for EHV cables with transmission lines［J］.Automation of Electric Power Systems，2005，29（10）：26－29.

［14］伍葉凱，鄒東霞.電容電流對差動保護的影響及補償方案［J］.繼電器，1997，25（4）：4－8.

WU Yekai，ZOU Dongxia.The effects and compensation method of capacitance current to differential protection［J］. Relay，1997，25（4）：4－8.

［15］南瑞繼保電氣有限公司.RCS－931A（B，D）型超高壓線路成套保護裝置［Z］.南京：南瑞繼保電氣有限公司，2003. NARI?RELAYS Electric Co.Ltd.RCS－931A（B，D）type ul?trahigh voltage line protective relay device［Z］.Nanjing：NARI?RELAYS Electric Co.Ltd.，2003.

［16］朱聲石.高壓電網繼電保護原理與技術［M］.3版.北京：中國電力出版社，2005：1－15.

ZHU Shengshi.Principles and techniques of protective relay for high voltage power system［M］.3rd ed.Beijing：China Electric Power Press，2005：1－15.

［17］高厚磊，安艷秋，江世芳.超高壓T接線路高精度故障測距算法研究［J］.電力系統自動化，2001，25（20）：35－39.

GAO Houlei.AN Yanqiu，JIANG Shifang.Study on accurate fault location algorithm for EHV TEED lines［J］.Automation of Electric Power Systems，2001，25（20）：35－39.

High Precision Single?ended Fault Location Method for Transmission Lines Based on Triangle Calculation in Special Wording Conditions

FENG Chang1，LI Feng1，SONG Shuang2，LU Shuai1，WANG Ke1
（1.Nanjing PANENG Technology Development Co.Ltd.，Nanjing 210031，China；（2.State Grid Jiangsu Electric Power Company Research Institute，Nanjing 211103，China）

Precise fault location is an important precondition of quick power supply restoration after transmission line fault occurs.In generally，concerning one?phase to ground fault，it is the transient resistance that causes that the impedance from where the relay is installed to where the fault occurs is caculated incorrectly.On such scenario，a double?ended fault location algorithm is preferred in order to acquire rather precise fault location result.Based on analyzing the source of additive impedance，this essay presents that under some special working conditions whereas double?ended fault location becomes invalid，single?ended fault calculation based on solving triangle calculation gives precise results.And this method can also be applied to hybrid parameter transmission lines which have both overhead lines and cables.The simulation and field data verified that the method has high precision.

single?ended fault location；double?ended fault location；impedance calculation；hybrid parameter transmission line；T type connection

TM772

：A

：2096－3203（2017）02－0110－06

馮 暢

馮 暢（1977—），男，江蘇南京人，工程師，從事繼電保護技術及其應用工作；

李 峰（1984—），男，山東濟南人，工程師，從事繼電保護技術及其應用工作；

宋 爽（1989—），男，安徽滁州人，工程師，從事繼電保護技術及其應用工作；

陸 帥（1987—），男，河南商丘人，工程師，從事繼電保護技術及其應用工作；

王 可（1987—），男，江蘇揚州人，工程師，從事繼電保護技術及其應用工作。

（編輯 徐林菊）

2016－12－04；

2017－02－19