數學思想在高中數學教學中的滲透管窺

江蘇省江陰祝塘中學(214415) 黃燕玉 ●

數學思想在高中數學教學中的滲透管窺

江蘇省江陰祝塘中學(214415) 黃燕玉 ●

數學思想是數學的靈魂．本文就三種數學思想的意義、作用和運用進行闡述，這對提高數學教學效果培養學生思維能力具有重要意義．

數學思想;轉化;數形結合;分類

隨著新課標改革進程的不斷推進，數學思想對于高中數學教學至關重要．在高中數學教學中滲透數學思想，有助于引導學生形成正確的數學思維，促進學生綜合素質的培養和發展．同時，高中數學新課標改革要求，高中數學需要以學生為主，教師在進行教學過程中注重激發學生的創新思維，引導學生養成自主思考和解決問題的習慣，以全面提升高中數學教學水平．數學思想具體可分為以下三種:轉化思想、數字與圖形結合思想和分類討論思想．

一、數學轉化思想

數學轉化思想，指的是實現數學知識的等價轉換．具體來講，教師在實際的數學教學過程中，在一定條件下將未知的數學知識轉化成為已知的數學基礎知識，進而解決未知的數學問題．教師在教學時做好引導者，引導學生利用已經掌握的知識點和數學技巧，簡化并解決復雜的數學問題．數學轉化思想簡便靈活，適用性強，在高中數學教學過程中得到了廣泛的應用．同時，數學轉化思想的應用需要以形形、數數和形數的聯系為基礎，結合教學目標進行合理化地轉化，在最大程度上培養學生的數學思維，提高學生靈活運用數學知識和技巧的能力．

比如，計算題:“設a、b屬于實數集，且滿足3a2+2b2=6a，求a的平方與b的平方之和的范圍．”教師在進行這道題的講解時，注重引導學生思考用等價轉換來減少或者消除未知變量．設一個參數k，使得k=a2+b2，那么保留一個主變量 a，則 b2=k－a2①，將①代入題中等式中，經過計算可得到關于主變量a的函數式，并根據題意a屬于實數集，可確定取值范圍，即得到答案:a的平方和b的平方之和屬于［0，4］．因此，從這個教學案例可以看出，數學轉化思想的靈活應用，可以引導學生運用數學轉化思想解決難度系數較高的數學計算題，以提升學生的數學思維能力，提高高中數學教學效率．

二、數字與圖形結合思想

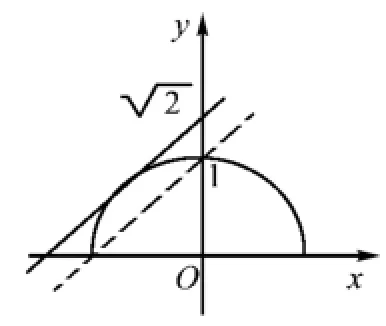
數字與圖形結合思想，就是在學習數學過程中實現數字與圖形的結合運用，使得幾何問題和代數問題可以相互轉化運用，以最簡單的方式解決數學問題．數字和圖形存在著一定的等量關系，可以通過數量和圖形的結合解決數學問題．數學題目大體上有兩種形式:一是通過圖形轉化將復雜的數字問題形象化、生動化;二是通過數字將圖形精確地描述，使得題意更加清楚明了．數字與圖形結合思想，體現了數學的靈活多變、嚴謹客觀．因此，在高中數學教學過程中，以數字和圖形結合的方式進行解題，明晰解題思路，大大提高學生的數學解題效率，實現學習和教學的事半功倍．

三、數學分類討論思想

分類討論，是在復雜的數學問題中找到規律，并對規律進行歸納和總結，接著進行針對性的分類分析和研究，從而全面地解決問題．分類討論的最終目的是找出問題中的規律，針對化地分析，歸納總結，探索出最佳解決問題的途徑和方式．分類討論思想具有條理性、歸納性和探索性等優勢，因此在現階段的高中數學教學中得到了廣泛的應用，這種思想有助于提高學生的綜合性自主思考和學習能力．

比如，計算題:“設函數f(x)=x2+|x－a|+1，x屬于實數集，判斷f(x)的奇偶性并求其最小值．”在分析此題時，需要考慮到絕對值符號和參數對f(x)的奇偶性影響．首先需要判斷參數a是否為零，分類如下:①當a等于零時，函數f(x)=(－x)2+|－x|+1=f(x)，此時函數為偶函數;②當a不等于零時，函數f(a)=a2+1，f(－a)=x2+2|a|+1．由于f(a)不等于f(－a)，此時函數既不是偶函數也不是奇函數．在求函數最小值時，需要分類討論去除絕對值符號，確保無遺漏無重復．先考慮x與a的關系，分類為x大于等于a和x小于a兩種情況，分別列出函數式，參數分別根據某一具體數值進行討論，最后在單調區間確定最小值．在這道例題的解題過程中，需要教師引導學生學會分類討論，并注意類別內部的細分．這樣的分類討論方式，有助于學生形成良好的歸納總結能力和數學邏輯思維，很大程度上避免了重復或遺漏，條理性極強，也極大程度上提高了解題效率，節省了時間．因此，分類討論思想在高中數學教學中需要引起教師的高度關注，著重服務于培養學生的數學能力．

綜上所述，在高中數學教學的過程中運用數學思想進行教書育人至關重要，有助于擴展學生的數學思維，形成良好的思維習慣，以提高高中數學的教學效果．因此，數學思想的應用滲透，需要各學校和教師高度重視，充分發揮其教學優勢，在潛移默化中培養學生的數學思維能力，使得數學思想和數學實踐相結合，實現綜合性應用．

G632

B

1008－0333(2017)03－0035－01