化工園區應急避難點選址評估模型應用研究*

陳國華，夏 浩，高子文

(1. 華南理工大學 安全科學與工程研究所，廣東 廣州 510640；2. 惠州大亞灣應急管理有限公司，廣東 惠州 516081)

0 引言

近年來，隨著我國化學工業和石油規模總量不斷擴大，現已建成了一批以天津、上海、惠州為代表的化工園區[1]。化工園區內危險源高度聚集，易發生火災、爆炸、毒氣泄漏等突發性災害事故，園區總體安全形勢不容樂觀，如：2015年4月6日，福建漳州古雷化工區發生嚴重的泄漏事故，該事故緊急疏散一萬多人[2]。當化工園區發生重大突發事件后，很難把所有居民都疏散到園區以外的安全地域，而科學合理地設置園區應急避難點，能夠有效地減少人員的傷亡和財產的損失[3]。應急避難點是化工園區發生重大突發事件后，避免人員傷亡和減少財產損失的一項重要舉措。目前，針對化工園區安全應急規劃的工作，主要集中在園區消防布局規劃、應急救援體系建設、應急能力評價和風險評估等方面[4]，針對化工園區應急避難點選址優化的研究并不多。祝愷[4]以化工園區內，各化工企業區域分布、避難人數需求、事故影響范圍和發生概率等因素，構建了后悔值模型；周曉猛等[5]綜合考慮距離、容量、配套設施、安全性和疏散道路5個方面的影響因素，提出了網絡優化模型；Anhorn等[6]以可達性分析為定量標準、適宜性和管理為定性標準，綜合考慮環境和基礎設施影響下，對地震后城市候選避難所進行了適宜性評價。綜合現有研究成果，現階段針對城市應急避難點的選址和優化研究較多，但對化工園區進行應急避難點選址評估的研究較少。因此，文本以廣東省某化工園區的調研工作為基礎，根據園區的工藝特點、空間布局、人口分布等因素，結合行業專家的意見，參考現有的標準和設計規范，構建化工園區應急避難點選址指標體系，給出定量化評估分級基準；為使化工園區應急避難點選址指標權重更加客觀、準確，運用博弈論的思想，對主、客觀權重進行組合賦權，計算出各指標貢獻率，從而建立有效的化工園區應急避難點選址評估模型。

1 化工園區應急避難點選址指標體系構建

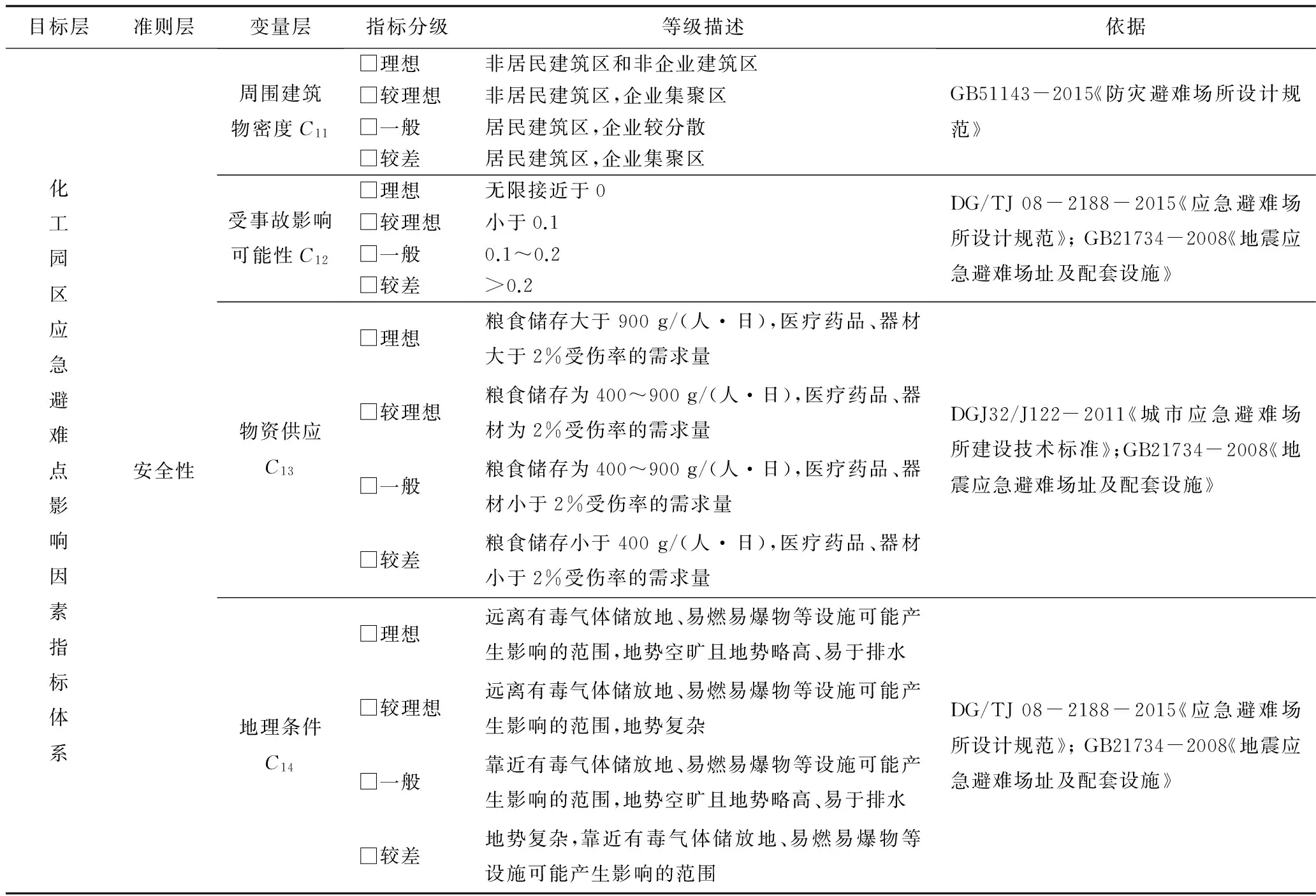
化工園區重特大事故發生后，為避免二次避難，受災人員需集中進行疏散和避難生活。科學合理地設置避難點選址，能夠極大限度地減少傷亡、降低災害帶來的社會影響。生活和醫療設施齊全、一定容量、疏散車輛易出入等特點是完善的應急避難點必備要求。參考GB 21734-2008《地震應急避難場所場址及配套設施》[7]、GB 51143-2015《防災避難場所設計規范》[8]、GB50016-2014《建筑設計防火規范》[9]等設計規范，綜合各項規范中的規定和要求，結合化工園區工藝特色、空間布局規劃等因素，從安全性、可達性、適宜性3個原則出發，建立化工園區應急避難點選址評估模型指標體系，如表1所示。

表1 化工園區應急避難點選址評估模型指標體系

2 化工園區應急避難點選址指標分級

根據對化工園區應急避難點選址指標體系的構建以及各指標不同安全等級，將各指標劃分為：理想、較理想、一般、較差4個不同安全等級，各等級的分值區間如表2所示。對照應急避難點選址的設計規劃及相關文獻，通過整理可以得到化工園區應急避難點“安全性”、“可達性”和“適宜性”各指標的分級，如表3、表4和表5所示。

表2 化工園區應急避難點影響指標分級準則

3 化工園區應急避難點選址貢獻率計算模型研究

3.1 指標權重獲取

根據實際情況，確定因素集的權重值大小，是化工園區應急避難點選址評估研究的核心。客觀賦權和主觀賦權是確定指標體系中各指標權重的常用方法[10]。客觀賦權過于依賴數據樣本，主觀賦權容易受專家個人偏好的影響[11]。為提高賦權的科學性，使權重既能夠反映專家意見又能夠兼顧客觀數據，采用AHP獲得主觀權重和信息熵方法來獲得客觀權重，借鑒博弈論的思想進行組合賦權優化指標權重。通過組合賦權的方式，比僅將主、客觀權重進行簡單加權平均的方法更加科學、合理[12]。

3.1.1 基于AHP的主觀賦權法

層次分析法(AHP)是綜合人們不同主觀判斷，并將其量化為定量分析結果的一種方法。以兩兩相互比較的方式，判斷目標層、準則層、方案層中各指標的相對重要程度，然后確定各指標在決策過程中所占的權重，從而為選擇最優方案提供依據[13-14]。

3.1.2 基于熵值法的客觀賦權法

熵值法是以信息熵理論為指導，通過指標的相對變化程度對系統整體的影響來確定指標權重，熵值法是客觀賦權中的一種重要方法和手段[15]。因此，化工園區應急避難場所選址指標體系的權重修正可采用熵值法獲得。根據信息熵的概念，將第j項指標的熵值定義為ej。

(1)

表4 化工園區應急避難場所“可達性”分級框架

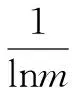
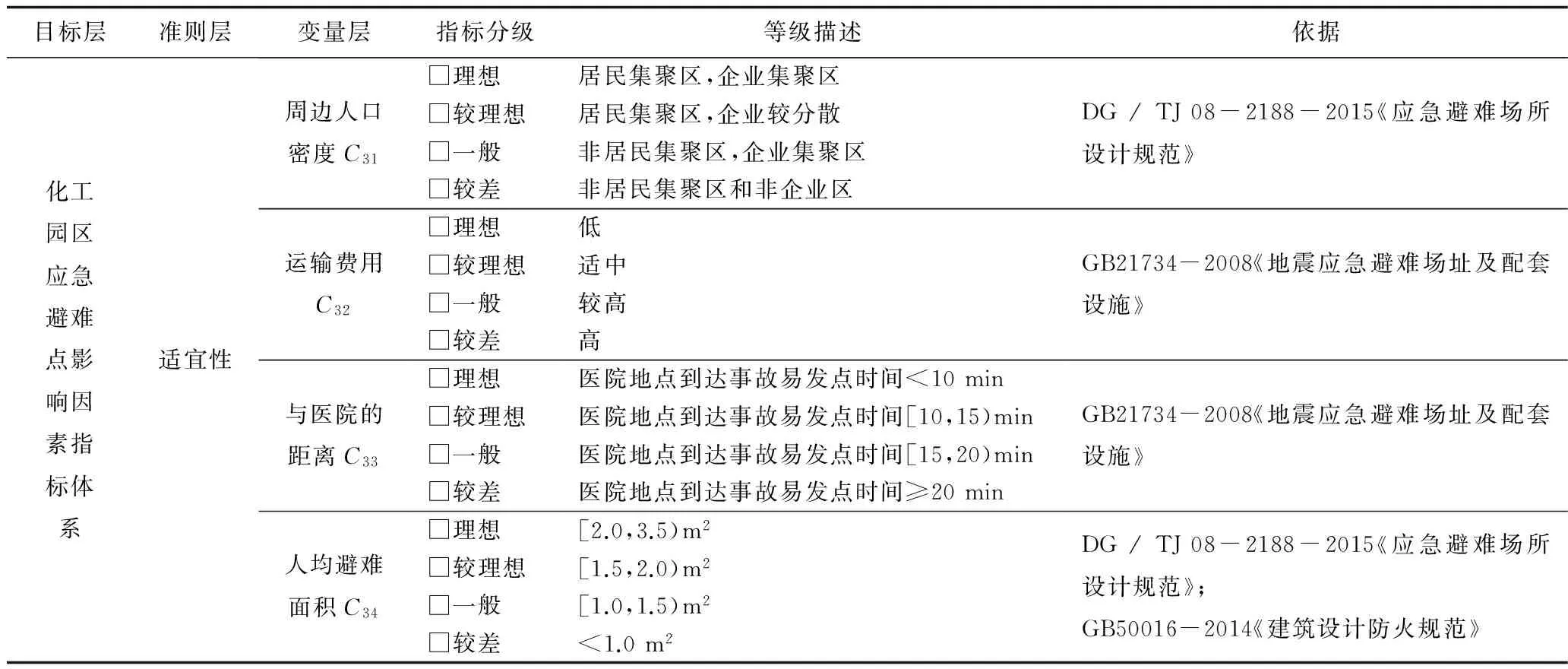
表5 化工園區應急避難場所“適宜性”分級框架

(2)

式中：gj為第j項指標的變異系數；n為指標的個數。

3.1.3 基于博弈論的組合賦權計算

為提高評估指標賦值權重的科學性和合理性，在AHP方法和熵值法的基礎上，采用博弈論結構模型，形成一種組合賦權新方法進行組合權重確定。

博弈論組合賦權的基本思想是使得綜合權重與各個基本權重之間離差最小化，尋找不同方法下得到的權重之間的均衡[16]。該方法能夠有效避免決策者的意愿偏好，反映出方案集中客觀數據對決策的貢獻度，有利于提高評估結論的可靠性。假設指標權重計算中，使用了L種方法，權重向量記為wk，線性組合系數記為αk，則權重向量的任意線性組合可以表示為：

(3)

通過優化對策模型中的線性組合系數αk，使w與每個wk的離差極小化。

(4)

根據矩陣的微分性質可知，為獲得w與每個wk的離差極小化，需采用式(4)的最優化一階導數條件如下：

(5)

通過式(5)，可求得(α1,α2,…αL)，然后由式(6)對其進行歸一化處理，即得到綜合權重向量w*：

(6)

(7)

3.2 貢獻率計算模型

化工園區應急避難點貢獻率是指“安全性”、“可達性”、“適宜性”等對園區應急避難點選址的影響程度。規定：當應急避難點影響因素對化工園區應急避難點選址的貢獻率為100/100=1時，則準則層所有因素均處于理想狀態，準則層及其對應的下級指標達到最高分100分。影響因素貢獻率要根據變量層因素的賦值確定，然后采取博弈論得到的權重，對各準則層對應變量層指標的分值。變量層最終分值依據式(8)確定。

(8)

式中：fki為變量層第k個因素第i個專家的賦值；fk為變量層第k個因素的分值；dki為變量層第k個因素對應賦分值的隸屬度。

準則層各因素加權分值見式(9)。

(9)

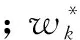
則園區應急避難點的安全性、可達性和適宜性的貢獻率為[17]：

(10)

4 實例應用

實例選取廣東省某化工園區，該園區總體面積約20 km2。園區北部以煉油、乙烯項目為中心，為工業用地區域，主要布置了石化產業生產裝置；南部為石化物流及港口發展區，往東為精細化工園區，往西為石化深加工區；園區地處亞熱帶，屬南亞熱帶季風性氣候，主導風向為東南風，園區及其園區周圍交通發達；地形總體上是呈“北-南”走向，地勢北高南低，園區居民主要集中在園區東側和西側，園區整體分布如圖1所示。

圖1 廣東省某化工園區分布Fig.1 Distribution map of a chemical industry park in Guangdong

應用上述評估模型，對該化工園區的應急避難點選址進行分級，根據相關專家對化工園區各變量層的指標賦分值，通過式(8)求出化工園區應急避難點選址各個變量的分值，如表6所示。以“可達性”相關下層指標的權重計算過程為例，通過基于AHP法的主觀賦權法得到的權重向量為：w1=(0.329，0.175，0.496)，以基于熵值法的客觀賦權得到權重向量為：w2=(0.381，0.304，0.315)；由基本權重集w={w1,w2}，并由式(3)～式(5)得到組合賦權方程組，如式(11)所示。

(11)

通過式(9)和式(10)計算得到基于博弈論的組合權重為w=(0.331，0.181，0.488)；以計算“平均通行時間”分值為例，調研時總共咨詢了5位專家，賦分值分別為：85,68,76,81,75，每位專家賦分值對應的隸屬度為0.2，那么“平均通行時間”分值為：85×0.2+68×0.2+76×0.2+81×0.2+75×0.2=77。

由表6中結果可知，指標貢獻率為：“可達性>適宜性>安全性”。因此，對于該園區的應急避難點選址，最關鍵因素是人員到達避難點的“可達性”，其次是“適宜性”和“安全性”。因此，該園區選擇避難點時，可以：

1)以“比鄰而居”為原則，應將避難點設置在該園區東側，靠近居民的位置，以方便居民的安全疏散，選址的位置應盡量毗鄰醫院，方便受傷人員的治療。

2)園區不應僅適用于特定的某類災種或某1類突發公共事件，應以多災種均可使用為原則，設置避難點；避難點位置應設置在沿東南方向的上風向處，減少對避難點造成的二次災害。

3)根據GB50489-2009《化工企業總圖運輸設計規范》、GB50187-2012《工業企業總平面設計規范》等設計規范和標準要求，化工園區應急避難點選址，應盡量靠近交通便利的位置，方便園區發生事故后，人員的安全疏散與應急救援。

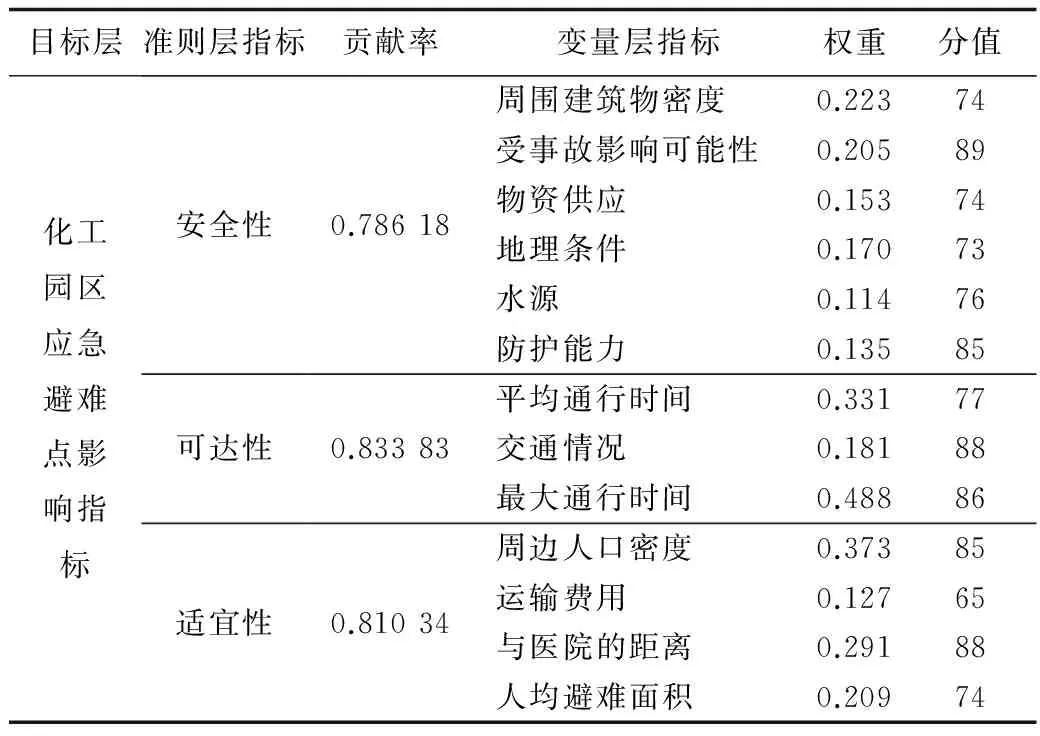
表6 廣東省某化工園區應急避難點影響指標及分值

5 結論

1)綜合考慮化工園區自身的工藝特點、空間分布等因素，構建化工園區應急避難點選址指標體系，運用博弈論對指標的主客觀權重加以組合，計算出指標貢獻率，使得選址評估結果更具合理性和適用性。

2)選取廣東省某化工園區作為選址評估對象，從評估結果可知，“可達性”對化工園區應急避難點的選址影響最大，應作為選址首要考慮因素。

3)從“安全性”、“可達性”、“適宜性”的角度進行研究還比較單一，并未考慮實際的避難點容量和服務范圍，這也是未來進一步深入研究的方向。

[1] 洪定一．2012年我國石油化工行業進展及展望[J]．化工進展，2013，32(3)：481-500．

HONG Dingyi. Development and Prospect of China's petrochemical industry in 2012[J]. Chemical Progress, 2013,32(3):481-500.

[2] 周俊飛.基于GIS的化工園區應急疏散輔助決策系統應用研究[D].廣州:華南理工大學，2015.

[3] 張培，張靖巖，王佳，等．城市社區應急避難場所區位配置模型研究[J]．中國安全科學學報，2015，25(6)：172-176．

ZHANG Pei, ZHANG Jingyan,WANG Jia,et al.Research on urban community emergency shelterlocationallocation model[J]. proceedings of the Chinese Journal of safety science, 2015, 25 (6): 172-176.

[4] 祝愷，熊濤，王青松，等．基于后悔值模型的化工園區應急避難場所選址分析[J]．火災科學，2015，24(3)：167-175．

ZHU Kai, XIONG Tao, WANG Qingsong,et al. Application of regret-model in site selectionfor evacuation shelters of chemical industry park[J]. Fire Science, 2015, 24 (3): 167-175.

[5] 周曉猛, 劉茂, 王陽. 緊急避難場所優化布局理論研究[J]. 安全與環境學報, 2006, 6(S1):118-121.

ZHOU Xiaomeng, LIU Mao, WANG Yang. Study on the optimal layout of emergency shelter[J]. Journal of safety and environment, 2006,6(S1): 118-121.

[6] Anhorn J, Khazai B. Open space suitability analysis for emergency shelter after an earthquake[J]. Natural Hazards & Earth System Sciences, 2015, 2(6):4263-4297.

[7] 中國地震局. 地震應急避難場所場址及配套設施: GB 21734-2008[S].北京：中國標準出版社，2008.

[8] 中華人民共和國住房和城鄉建設部.防災避難場所設計規范: GB 51143-2015[S].北京：中國建筑工業出版社，2016.

[9] 中華人民共和國公安部.建筑設計防火規范:GB50016-2014 [S].北京：中國計劃出版社，2015.

[10] 蔣艷，岳超源．方案排序對權重比例變化的敏感性分析[J]．華中科技大學學報(自然科學版)，2002，30(8)：24-26．

JIANG Yan, YUE Chaoyuan.Sensitivity analysis of scheme ranking to weight ratio[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2002,30 (8):24-26.

[11] YI W, ?zdamarb L. A dynamic logistics coordination model for evacuation and support in disaster response activities[J]. European Journal of Operational Research, 2007, 179(3):1177-1193.

[12] 鄭紹羽, 李素芹. 混合型指標基坑支護方案優選的改進TOPSIS法[J]. 中國安全科學學報, 2014, 24(5):98-103.

ZHENG Shaoyu,LI Suqin.An improved TOPSIS method for the optimization of mixed type index foundation pit payment scheme[J]. proceedings of the Chinese Journal of safety science, 2014, 24 (5): 98-103.

[13] 竇站, 張勇, 張明廣,等. 基于AHP-模糊方法的某化工園區應急能力評估[J]. 安全與環境學報, 2015, 15(2):29-34.

DOU Zhan,ZHANG Yong,ZHANG Mingguang, et al.Emergency response capacity assessment of achemical industrial park based on AHP-Fuzzymethod[J]. Journal of safety and environment, 2015 (2): 29-34.

[14] 陳國華，劉爽，王新華．基于組合賦權法的塔式起重機定量風險評估及應用[J]．起重運輸機械，2015(4)：62-68．

CHEN Guohua,LIU Shuang,WANG Xinhua. Quantitative risk assessment and application of tower crane based on combination weighting method[J]. Mathematicsin Practice and Theory, 2015(4):62-68.

[15] 鄧雪，李家銘，曾浩健，等．層次分析法權重計算方法分析及其應用研究[J]．數學的實踐與認識，2012，42(7)：93-100．

DENG Xue,LI Jiaming,ZENG Haojian,et al. Research on computation methods of AHP weight vectorand its applications[J]. Mathematicsin Practicesand Theory, 2012, 42 (7): 93-100.

[16] 路遙，徐林榮，陳舒陽，等．基于博弈論組合賦權的泥石流危險度評價[J]．災害學，2014，29(1)：194-200．

LU Yao, XU Linrong, CHEN Shuyang,et al. Combined weight method based on game theory fordebris flow hazard risk assessment[J]. Disaster science, 2014, 29 (1): 194-200.

[17] 李傳貴，巫殷文，劉建，等．化工園區安全容量計算模型研究[J]．中國安全生產科學技術，2009，5(3)：25-29．

LI Chuangui, WU Yinwen,LIU Jian,et al. Study on the calculation model of safety capacity of Chemical Industry Park[J].China safety science and technology. 2009, 5 (3): 25-29.