基于分組策略的補貨配送問題優化模型*

劉艷秋， 曹 歌， 張 穎， 李 佳

(沈陽工業大學 a.理學院， b.信息科學與工程學院， 沈陽 110870)

信息科學與工程

基于分組策略的補貨配送問題優化模型*

劉艷秋a， 曹 歌a， 張 穎a， 李 佳b

(沈陽工業大學 a.理學院， b.信息科學與工程學院， 沈陽 110870)

針對已存在的供應鏈環境下較少考慮補貨配送問題中的分組配送策略，結合大量零售商對單一產品需求量不同等特點，引入分組的決策變量.根據配送中心補貨周期與配送次數的函數關系，以最小化三級供應鏈系統的平均總成本為目標，構建了帶有配送中心能力約束的補貨配送優化模型.根據優化模型的特點，利用改進的遺傳算法求解模型，并進行了數據仿真試驗.結果表明，該優化模型能為配送中心提供一種有效的分組配送方案，選擇的優化算法更穩定快捷，能為企業提供有益的管理啟迪.

物流；供應鏈；配送中心；補貨配送優化模型；補貨周期；配送次數；分組策略；遺傳算法

供應鏈是產品由生產端傳送到客戶端過程中所歷經的各個環節，是由企業共同構建的鏈狀網絡.配送中心作為供應鏈中連接上游供應方和下游需求方的關鍵一環，對整個供應鏈的管理有著重要影響.其中，配送中心涉及的補貨與配送問題是影響其發展的兩個關鍵問題.由于在補貨與配送問題中考慮的庫存與運輸成本存在著一種此盈彼虧現象，因此在研究中常將二者聯合探討，益于供應鏈系統的集成決策，實現配送中心資源配置與客戶需求的高度結合，提高客戶服務水平.

目前，研究供應鏈中補貨配送問題的文獻有很多.在研究此問題時，大多數文獻采用整數比周期策略和二次冪周期策略等補貨策略進行補貨[1-2]，以補貨和配送相關總成本為目標函數[3-4]，并建立數學模型，利用差分進化算法和遺傳算法等優化算法來求解模型[5-7].閔杰等[8]將變質性商品的需求量伴隨庫存的變化而變化這一特點考慮到補貨配送問題中，從而使構建的模型更符合實際需要；林峰等[9]以易腐品為研究對象，將時間、載重成本等因素引入到模型中，構建了基于需求分割配送決策下的補貨配送優化模型；劉玉偉等[10]建立補貨配送模型時考慮了分組配送策略，從而優化了總成本.在現有補貨配送問題的研究中忽略了物流的具體配送過程，常默認為運輸車輛依次或一對一地為零售商進行送貨，在針對大量異質零售商環境下，采用這兩種方法送貨耗時長、成本高且會耽誤零售商的正常運營，因此需要在物流配送過程中引入分組配送策略.文獻[10]雖然考慮了分組配送，但其直接給定了分組數和組與組之間配送周期關系，文獻[10]的分組決策仍具有局限性.

本文研究了在確定需求下零售業配送中心單一產品補貨與配送聯合優化問題，在研究此問題中引入了分組的決策變量，通過采用分組策略有效改善物流配送過程，制定出配送中心最佳的補貨周期和每組配送次數，合理分配配送中心資源并選擇優化的路徑進行配送，從整體上協調供應鏈管理，增加企業的競爭力.模型涉及到三個決策變量，可能會造成求解復雜解空間的問題，本文在求解時先進行降維處理，再利用遺傳算法進行運算.

1 補貨配送優化模型

1.1 問題描述

考慮由一個供應商、一個配送中心、多個零售商組成的三級供應鏈系統(簡稱1-1-N系統).供應商負責提供單一產品，配送中心在一定周期內對自身進行補貨，并且配送中心根據匯總的各零售商提供的補貨產品信息為各零售商制定配送策略.該供應鏈中系統產生的成本主要有配送中心的訂貨成本、庫存成本和配送成本，以及零售商的庫存成本.目標是以最小化系統平均總成本來制定配送中心補貨策略和配送策略，使配送中心資源得到合理利用.供應鏈物流網絡結構如圖1所示.

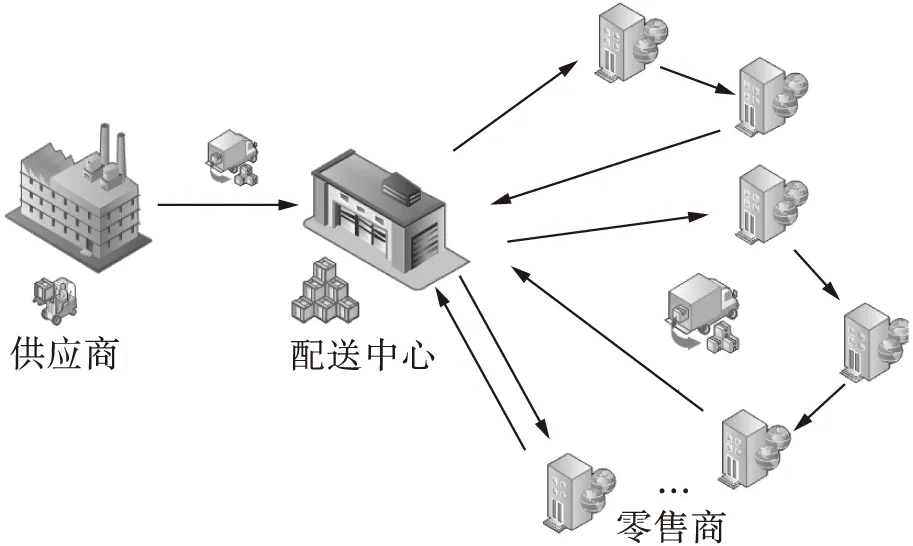
圖1 供應鏈物流網絡結構Fig.1 Structure of supply chain logistics network

1.2 變量描述及條件假設

在建模過程中涉及到的變量分別為：N為零售商的集合；I為零售商分組的集合；S為配送中心的固定訂貨成本；C0為配送中心單位貨物的存儲費；C1為零售商單位貨物的存儲費；C2為單位距離車輛運輸費；rij為第i組中第j個零售商每天的需求量；Q1為配送中心單位車輛的最大載重量；y為配送中心在此種產品上可供調配的最大車輛數；D為配送中心單位車輛的最大行駛距離；di(j-1)，ij為第i組中第j-1個零售商到第j個零售商的距離(其中，di0，ij為配送中心到第j個零售商的距離).決策變量分別為：T為配送中心的補貨周期；pi為配送中心在補貨周期內為第i組零售商進行配送的次數，同一組的零售商配送次數相同，不同組的零售商配送次數互不影響，其值取整數；xij為選擇為第i組中第j個零售商配送時其值為1，否則為0.

模型的建立基于以下假設：1)配送中心的補貨提前期很短，可以忽略不計；2)在此三級供應鏈中只考慮對單一產品進行補貨，且不出現送貨延遲或缺貨情況；3)每條線路上只需一輛車進行配送，每個零售商只允許出現在一條線路上；4)零售商每天的需求量是連續均勻的，且需求量確定.

1.3 模型建立

在由一個供應商、一個配送中心、多個零售商組成的三級供應鏈中，配送中心產生的物流費用主要包括訂貨成本、庫存成本和配送成本，其中，訂貨成本和庫存成本為

(1)

配送成本主要是車輛行駛費，即

(2)

零售商產生的物流費用主要是庫存成本，即

(3)

綜合配送中心訂貨成本、庫存成本和配送成本，以及零售商的庫存成本，三級供應鏈系統的單位時間總成本為

(4)

建立配送中心補貨配送聯合優化模型，其表達式為

(5)

s.t.

(6)

(7)

(8)

(9)

(10)

xij=0，1 ?i∈I，j∈N

(11)

其中，補貨配送優化模型的目標函數式(5)為三級供應鏈系統產生的單位時間物流總成本，包括配送中心的訂貨成本、庫存成本和配送成本，以及零售商的庫存成本；式(6)表示時間約束，即配送中心的配送周期要比配送中心的補貨周期小；式(7)表示第i組中的零售商配送時的行駛距離不能超過車輛的最大行駛距離；式(8)表示第i組中零售商配送時的配送量不能超過單位車輛的最大載重量；式(9)表示配送中心每次訂貨總量不能超過配送中心的最大服務能力；式(10)限制每個零售商只能出現在一個分組中；式(11)為變量約束，即0-1變量.

2 算法設計

2.1 最佳補貨周期

根據補貨配送模型中的目標函數可得

(12)

(13)

2.2 改進的遺傳算法

本文研究的補貨配送聯合優化問題是強NP問題，現有文獻對此類問題多采用智能優化算法進行求解.本文提出的補貨配送優化模型求解的難度是考慮零售商的不同分組和每組配送次數的選擇，在進行劃分時會受到零售商需求量、車輛的載重量和行駛距離等因素的影響，并且在優化模型中將會遇到復雜的求解空間問題.綜合以上考慮，本文選取遺傳算法并結合自身模型特點對其進行改進來求解模型.遺傳算法具體操作流程如下：

1) 初始化種群與染色體編碼.設置初始時刻t=0，種群規模NP=100，最大遺傳代數NG=200.染色體編碼使用二進制遺傳編碼[11]，采用以零售商為基因、零售商的組號xij和每組的配送次數值pi為基因值的編碼方式，xij取值為1或0，pi取值上限為10.

2) 適應度計算.模型中目標函數為求最小值問題，在運算時轉化為求目標函數的最大值.

3) 選擇操作.采用輪盤賭選擇法[12]，選擇適應性較高的個體作為優秀個體進行遺傳，適應性較高的個體得到的繁殖機率較大.

4) 交叉與變異.采用雙切點交叉操作，設置交叉概率Pc=0.9；變異則是選取種群中個體的某些基因位值，并將選取的位值進行變化，設變異概率Pm=0.08.

5) 判斷停止條件.若最大遺傳代數達到200，則停止計算，輸出最優解.

3 仿真試驗與對比分析

在由一個供應商、一個配送中心和8個零售商組成的三級供應鏈算例中，供應商提供單一產品，配送中心的固定訂貨成本為200元，車輛行駛單位距離的運輸費為0.5元/km，每輛車載重3t，配送中心有5輛車可供調配，車輛的最大行駛距離為1 000km，零售商、配送中心的數據以及節點間距如表1、2所示.

表3為不同分組下的配送中心最佳決策.由表3可知，當配送中心分2組進行配送時，配送中心最佳補貨周期為5.782 6d，零售商5為一組在補貨周期內配送一次，零售商1、2、3、4、6、7、8為一組在補貨周期內配送兩次，此時的系統平均總成本為190.40元；當配送中心分3組進行配送時，配送中心最佳補貨周期為5.821 6d，零售商1、2、4為一組在補貨周期內配送一次，零售商3、6、7為一組在補貨周期內配送兩次，零售商5、8為一組在補貨周期內配送一次，所得到的系統平均總成本為219.19元.通過對比可以發現，分2組時系統平均總成本最小，因此，配送中心在為零售商進行配送時分2組更好.

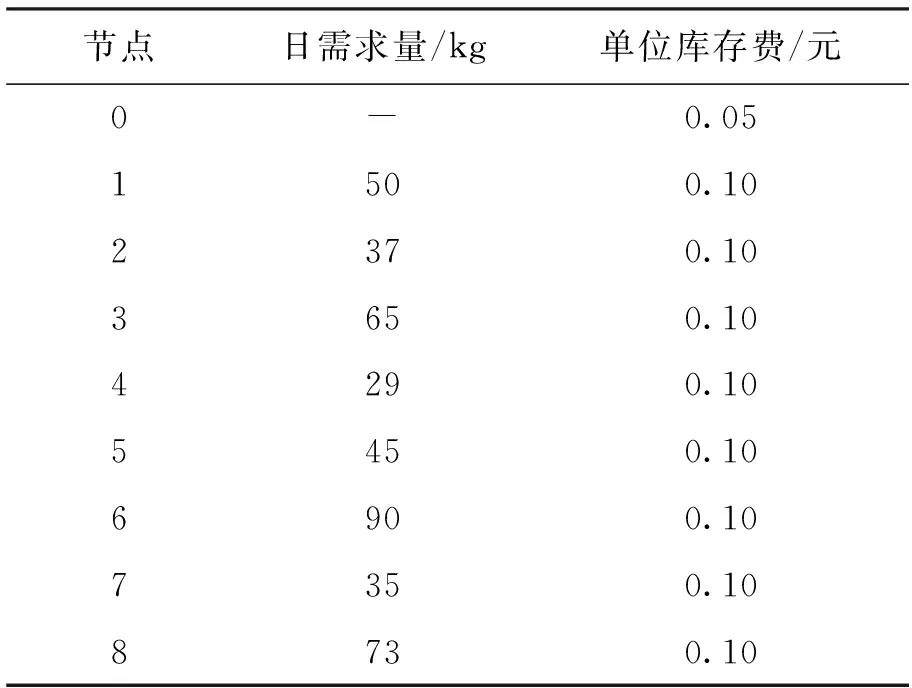
表1 零售商參數Tab.1 Parameters for retailers

表2 配送中心和零售商節點間距Tab.2 Node distances between distribution centers and retailers km

表3 不同分組下的配送中心最佳決策Tab.3 Optimal decisions of distribution center under different grouping conditions

表4給出了采用文獻[10]中的分組策略與本文中的分組策略進行對比的結果，可以發現本文中的分組策略較優，使得系統平均總成本更小.

4 結 論

配送中心科學地進行補貨與配送可以有效提高企業的效率，減少企業成本，因而補貨與配送問題也逐漸引起人們的重視，其研究也更具有學術價值.對于配送中心來說，采取何種補貨策略與配送策略是解決問題的重點.本文在設計模型時考慮到靈活分組因素，以優化配送中心的訂貨成本、庫存成本和配送成本，以及零售商的庫存成本為目標，建立更貼近實際需求的配送中心補貨配送優化模型，其結果證實了該模型的有效性，采用的分組配送策略能使企業達到節約成本的目的，并促進企業快速整合內部資源來響應客戶需求，提升企業的服務質量.

表4 分組策略比較Tab.4 Comparison in grouping strategies

注：*表示采用文獻[10]中的分組策略.

(FU Cheng-hong，FU Zhuo.A combined strategy of fixed-partition and integer-ratio for inventory routing problem [J].Journal of Railway Science and Engineering，2013，10(6)：103-108.)

[2]李莉英，王勇，楊金.一類多對多物流系統的運送頻率選擇優化問題研究 [J].運籌與管理，2012，21(2)：92-99.

(LI Li-ying，WANG Yong，YANG Jin.Shipping frequencies selection in a many-to-many logistics system [J].Operations Research and Management Science，2012，21(2)：92-99.)

(ZHAO Da，LI Jun，MA Dan-xiang，et al.Optimal strategy of stochastic demand inventory routing problem and algorithms [J].Journal of Management Sciences in China，2014，17(5)：14-24.)

[4]Abdul-Jalbar B，Segerstedt A，Sicilia J，et al.A new heuristic to solve the one-warehouse N-retailer problem [J].Computers and Operations Research，2010，37(2)：265-272.

(WANG Lin，DUN Cai-xia，ZHANG Jin-long.Integrated joint replenishment and distribution model using hybrid differential evolution algorithm [J].Chinese Journal of Management Science，2012，20(3)：86-93.)

[6]Cha B C，Moon I K，Park J H.The joint replenishment and delivery scheduling of the one-warehouse，n-retailer system [J].Transportation Research Part E，2008，44(5)：720-730.

[7]Li J X，Chu F，Chen H X.A solution approach to the inventory routing problem in a three-level distribution system [J].European Journal of Operational Research，2011，210(3)：736-744.

(MIN Jie，FU Juan，OU Jian，et al.An optimal inventory-distribution model with deteriorating items and inventory-level-dependent demand [J].Industrial Engineering Journal，2014，17(6)：54-61.)

[9]林峰，賈濤，高艷，等.考慮分割配送的易腐品一體化庫存路徑問題 [J].工業工程與管理，2015，20(5)：45-53.

(LIN Feng，JIA Tao，GAO Yan，et al.Integrated inventory routing problem with split-delivery for deteriorating items [J].Industrial Engineering and Management，2015，20(5)：45-53.)

(LIU Yu-wei，JIA Tao，GAO Yan.The integrated production-distribution inventory model considering grouping strategy in the supply chain [J].Industrial Engineering and Management，2015，20(2)：7-15.)

[11]劉艷秋，焦妮，張義華.基于低碳理念的多級物流網絡優化設計 [J].沈陽工業大學學報，2015，37(4)：404-409.

(LIU Yan-qiu，JIAO Ni，ZHANG Yi-hua.Optimization design for multi-level logistics network based on low carbon concept [J].Journal of Shenyang University of Technology，2015，37(4)：404-409.)

[12]李志，周愉峰.考慮中斷風險與庫存成本的分銷網絡設計模型 [J].運籌與管理，2014，23(6)：136-143.

(LI Zhi，ZHOU Yu-feng.Distribution network design problem considering inventory cost under the risk of disruptions [J].Operations Research and Management Science，2014，23(6)：136-143.)

(責任編輯：鐘 媛 英文審校：尹淑英)

Optimization model for replenishment and distribution problems based on grouping strategy

LIU Yan-qiua,CAO Gea,ZHANG Yinga,LI Jiab

(a.School of Science,b.School of Information Science and Engineering,Shenyang University of Technology,Shenyang 110870,China)

Aiming at the fact that the grouping distribution strategy in the replenishment and distribution problems is not fully considered in the existing supply chain,a decision variable for grouping was introduced in combination with such features that a large number of retailers have different demands on a single product.According to the function relationship between the replenishment cycle and delivery times,the average total cost of a minimized three-level supply chain system was taken as the objective,and the optimization model for the replenishment and distribution with the capacity constraints of distribution center was established.According to the characteristics of this optimization model,the improved genetic algorithm was used to solve the model,and the numerical simulation test was carried out.The results show that the proposed optimization model can provide an effective grouping strategy for the distribution center,and the selected optimization algorithm is more stable and rapid,which can provide the beneficial management enlightenment for companies.

logistics;supply chain;distribution center;replenishment and distribution optimization model;replenishment cycle;delivery time;grouping strategy;genetic algorithm

2016-08-31.

國家自然科學基金資助項目(70431003)；沈陽市科學技術計劃項目(F14-231-1-24).

劉艷秋(1963-)，男，吉林四平人，教授，博士生導師，主要從事復雜系統可靠性建模與優化等方面的研究.

19 18∶00在中國知網優先數字出版.

http：∥www.cnki.net/kcms/detail/21.1189.T.20170119.1800.022.html

10.7688/j.issn.1000-1646.2017.02.09

TP 301

A

1000-1646(2017)02-0165-05