六自由度串聯機器人動態誤差分析

侯小雨, 朱華炳, 王魯平

(合肥工業大學 機械工程學院,安徽 合肥 230009)

六自由度串聯機器人動態誤差分析

侯小雨, 朱華炳, 王魯平

(合肥工業大學 機械工程學院,安徽 合肥 230009)

由于機器人在工作過程中受負載、連桿自重等因素影響,其連桿產生變形會引起末端執行器的位置誤差。針對該問題,文章以FANUC M-10iAe機器人為研究對象,采用仿真與實驗相結合的方法,以提高機器人定位精度為目標展開研究。在ADAMS環境中進行動力學仿真,對機器人工作過程中變載荷引起的動態誤差進行分析;通過自主設計的測量裝置及變載荷方盒進行試驗,結果證實了動力學仿真的準確性;在誤差分析結果的支撐下,設計開發了基于人機交互的誤差補償界面并通過了實例驗證。

串聯機器人;柔性;動態誤差;ADAMS仿真;負載;誤差補償界面

隨著工業技術的不斷發展,串聯機器人作為一種典型的柔性自動化設備已被廣泛應用于焊接、碼垛、噴涂等領域,引領產業升級和轉型。目前工業機器人的重復定位精度較高,而絕對定位精度一般都比較低[1],這樣的絕對定位精度水平已不能滿足一些高精度操作作業場合的需要。國內外從20世紀80年代就開始了這方面的研究工作,形成了多種誤差分析方法,通過標定的方法提高機器人絕對定位精度[2-4],研究機械臂自重和負載變化引起機器人末端執行器的位置誤差[5-7]。

本文針對工業機器人在不同碼垛任務中負載的不同,考慮機器人的連桿一般都具有一定的柔性,通過分析末端負載這一動態因素對機器人精度造成的影響,達到對誤差進行預測的目的;設計開發的誤差補償界面可以為機器人誤差補償提供參考,進而提高機器人的絕對定位精度。

1 動態誤差分析

1.1 FANUC M-10iAe機器人誤差傳遞模型

根據D-H參數法,確定了FANUC M-10iAe機器人各關節坐標系,將連桿坐標系按坐標系編號依次變換,建立四階變換矩陣表征其與前一桿件坐標系的變換關系,得到機器人連桿參數的D-H參數表,見表1所列。

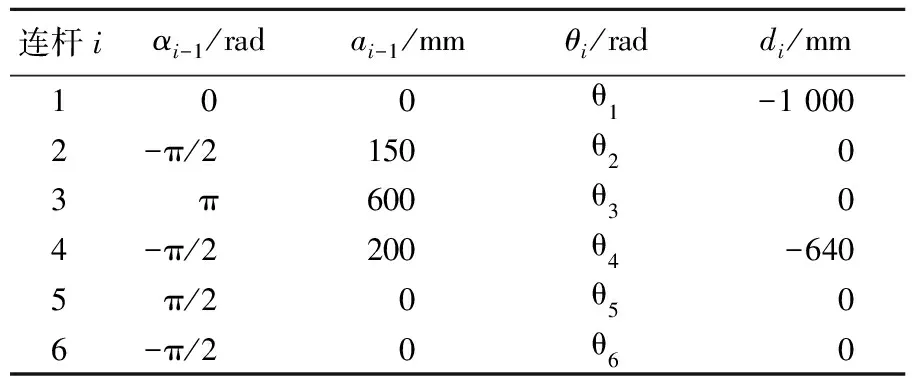
表1 FANUC M-10iAe機器人D-H參數表

由D-H參數和齊次變換公式可依次求得兩桿之間的位姿矩陣Ti,進而得出機器人從基座到末端執行器的總齊次變換公式為:

(1)

其中,nx、ny、nz為末端執行器法向矢量;ox、oy、oz為方向矢量;ax、ay、az為接近矢量;px、py、pz為位置坐標。

由(1)式可得出末端執行器位置坐標與各關節轉角的關系為:

200cosθ1cosθ2+600cosθ1，

200sinθ1cosθ2+600sinθ1，

1.2 FANUC M-10iAe機器人動力學模型

FANUC M-10iAe機器人是一種六自由度串聯機器人,具有6個轉動關節。其本體由基座、立柱、大臂、小臂、手腕、手部組成,各轉動關節與減速器相連并由伺服電機驅動,可以滿足驅動力矩較大和運動定位準確的要求。利用SolidWorks軟件對該機器人進行三維實體建模,得到機器人虛擬裝配體,然后導入ADAMS中。

機器人的2、4連桿因其桿長的原因產生的變形量比其他連桿大,對末端精度造成的影響也就更大,同時為了適當簡化模型,本文僅對三維實體模型中的2、4連桿進行柔性化處理。首先利用ADAMS/Flex柔性體模塊生成2、4連桿的柔性體[8],提取六階模態,生成模態中性文件MNF,然后將MNF文件導入到ADAMS軟件中替代原來的剛性構件,得到剛柔耦合動力學模型,如圖1所示。

圖1 FANUC M-10iAe機器人剛柔耦合動力學模型

1.3 驅動函數

在本文研究的機器人碼垛任務中,為了依據預先規劃的軌跡對動力學模型進行驅動,可近似認為機器人在固定時間內的運動是逐步和階躍的。

在Matlab中模擬實際碼垛完成軌跡規劃,然后利用規劃軌跡中各關節轉角的變化值生成樣條曲線,即各關節的驅動函數[9]。具體步驟如下:利用Matlab在碼垛任務過程中每隔0.056 s計算1次各關節轉角,得到各關節轉角變化數值,在ADAMS中通過Test Data 外部輸入數據依次導入各關節角位移數值,并創建相應的Spline樣條函數曲線。其中關節1的樣條函數曲線SplneE-1如圖2所示。其余5個關節的樣條函數曲線創建方法同上,此處不再贅述。最后將6個關節樣條函數依次施加到對應關節轉動副上,完成對動力學模型的驅動[10]。

圖2 關節1樣條函數曲線Spline-1

1.4 基于實際工況的機器人末端載荷的施加

研究對象FANUC M-10iAe機器人可搬運質量的最大值為10 kg,結合實際驗證試驗方案中末端載荷的變化情況,設定末端載荷變量的10個取值。在ADAMS中分別針對10組末端載荷變量進行模擬仿真,得到仿真曲線,下面僅列出末端載荷為8.889 kg時末端執行器對稱中心處位移曲線,如圖3所示。

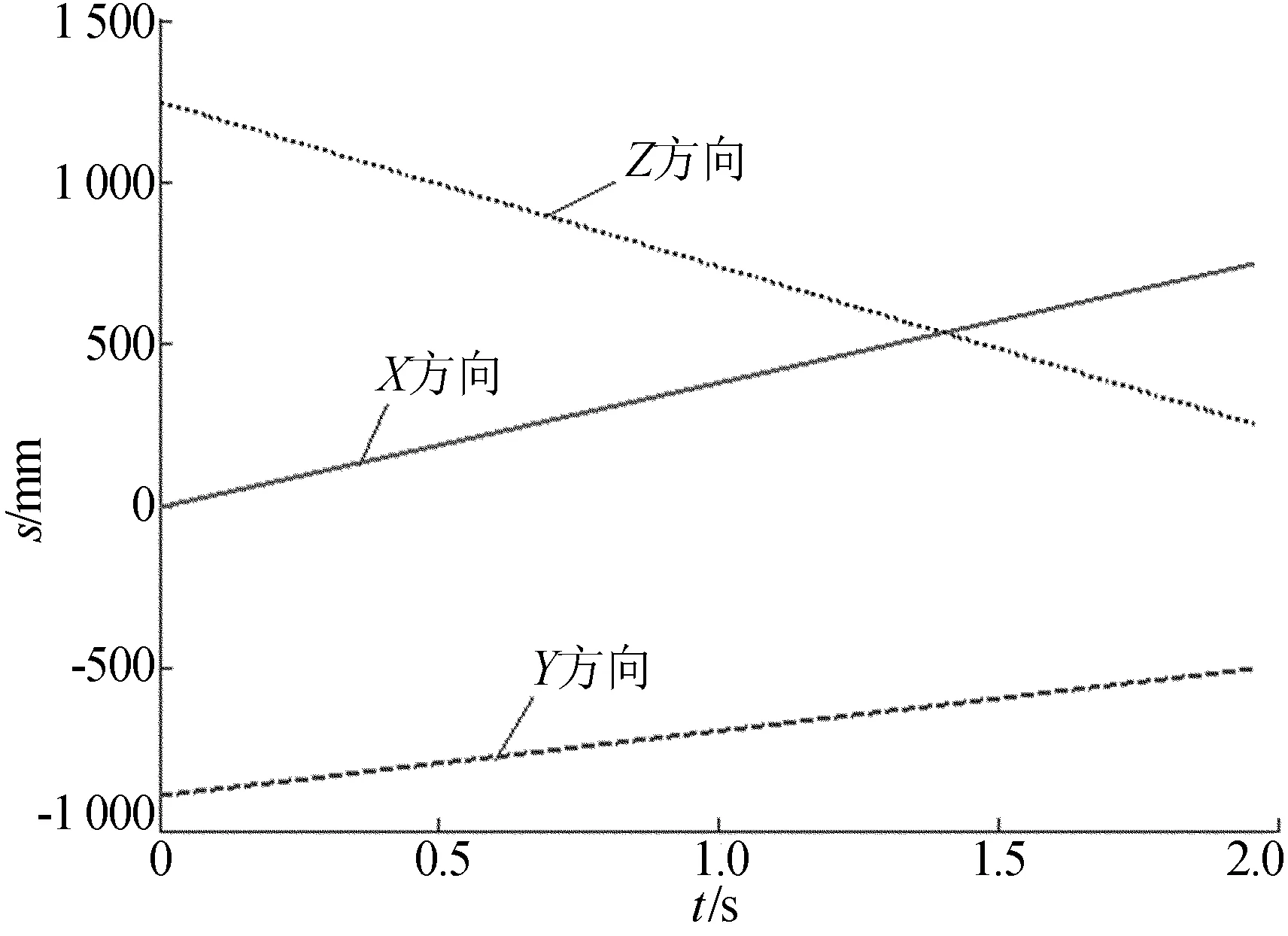
圖3 末端載荷為8.889 kg時末端位移仿真曲線

通過對比末端執行器對稱中心處Marker點的坐標和末端執行器的理論目標點位置坐標(750.000,-500.000,250.000),可以得到不同末端載荷下動態誤差量的大小,見表2所列。

表2 動力學仿真得到的動態誤差值 mm

2 誤差驗證試驗

2.1 試驗方案設計與數據采集

本試驗通過自主設計的測量裝置及變載荷方盒,借助FANUC M-10iAe機器人進行試驗研究。其中測量裝置由3個SGC-W10微位移光柵傳感器和1個測量臺架組成。3個傳感器分別測量X、Y和Z方向的位移偏差;方盒內部可按需要裝入0～9枚砝碼,以此來調節末端載荷的質量[11]。通過該試驗可以得到機器人動態誤差與末端載荷的關系。

在試驗過程中需要通過示教的方法運行并控制末端執行器姿態不發生改變,以保證3個傳感器測量頭始終與方盒3個表面分別垂直,避免末端執行器中心點產生旋轉量而對試驗結果產生影響。本試驗采用的傳感器分辨率為1 μm,FANUC M-10iAe機器人重復定位精度為±0.08 mm,因此選擇該位移傳感器測量機器人定位精度是滿足要求的。傳感器輸出的TTL方波通過數顯表和RS235串口與計算機通訊,傳感器輸出信號用Data Acquisition數據采集工具箱進行采集和處理。試驗過程中,機器人末端執行器重復運行至試驗數據測量點,傳感器測得X、Y和Z方向的位置偏移量由計算機記錄并保存。具體試驗流程如圖4所示。

圖4 試驗流程

2.2 試驗數據處理與分析

試驗過程中機器人自定義空間坐標原點位于基座的內部,其具體位置無法測量,故此處采用距離誤差原理對試驗數據進行處理。對測量組的試驗數據分別求解其在空間坐標系中算術平均誤差值,將這些相對測量臺架的誤差偏移項作為對仿真數據驗證的評價指標[12]。由于試驗結果與動力學仿真得到的結果需要進行對比,故此處對X、Y和Z方向上的算術平均誤差值分別進行求解,公式如下:

(2)

其中,xi、yi、zi為試驗測得3個傳感器的位置偏移量;x、y、z為方盒3個測量面理論上引起3個傳感器的位置偏移量;k為試驗測量次數。

下面展開對x、y、z的計算工作,本文僅對X、Z方向的計算提供圖解,如圖5所示。

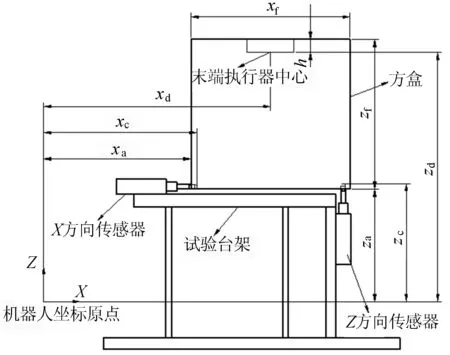
圖5 X、Z方向計算圖解

首先利用機器人示教盒上讀出試驗點機器人的位置數據(xd,yd,zd),測量變載荷方盒的外形尺寸值xf、yf、zf和方盒安裝板上的機器人末端執行器安裝孔深度h,求出在試驗點處方盒的3個測量面與機器人坐標原點的理論距離(xa,ya,za),計算公式如下:

(3)

測出3個傳感器測量頭在世界坐標系下的坐標(xc,yc,zc)，即可求得方盒3個測量面理論上引起3個傳感器的位置偏移量,分別為:

(4)

由(4)式計算得出x=1.26 mm,y=0.51 mm,z=6.04 mm。

將上述數據和試驗測得的數據代入(1)式，即可得出每個測量組在X、Y、Z方向上的算術平均誤差值,見表3所列。

表3 X、Y、Z方向上的平均誤差值 mm

在X、Y、Z方向上對仿真與試驗數據的誤差均值進行對比,由于篇幅有限，本文僅列出X方向對比結果,如圖6所示。

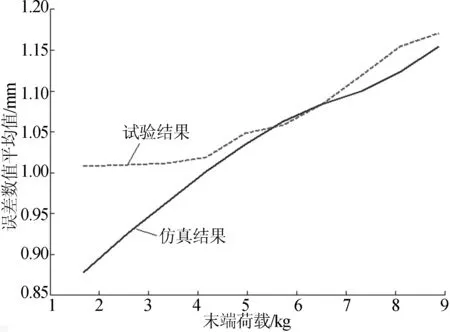
圖6 X軸方向仿真結果與試驗結果對比

由分析對比結果可知,動力學仿真對誤差變化的預測趨勢是正確的,即總體誤差隨著末端載荷的增大而增大。在X、Y、Z方向上試驗誤差均值相對于試驗數據均值的偏差分別為3.44%、7.34%、15.16%。其中,Z方向上首組試驗點仿真結果與試驗結果相差較大,屬于異常點,為了得到比較符合實際的擬合結果,需要除去Z方向上的首組數據,則Z方向上誤差偏差降低至6.85%,該結果是比較符合實際情況的。

3 誤差補償界面

3.1 誤差補償界面的設計

針對機器人實際應用場合柔性較強的現狀,本文設計的誤差補償界面具備的用戶定義輸入變量主要有4項,分別為目標機器人型號、末端載荷質量、誤差量擬合方式、碼垛作業區間。基于仿真與試驗得到的綜合誤差情況,在用戶自定義輸入變量后完成補償量的計算輸出。誤差補償界面的布局如圖7所示。

圖7 誤差補償界面布局

實現補償界面的基本機制是對控件的屬性編程,通過回調函數(callback)來完成事件驅動。用戶輸入參數后通過句柄傳遞至運算模塊,點擊相應按鈕控件,觸發相應的計算和繪圖功能,結果將在文本框與圖形窗口進行顯示。

為了通過有限次的變載荷模擬試驗來預測機器人在負載允許范圍內的誤差變化情況,在Matlab中使用最小二乘法擬合各末端載荷與相應誤差值的關系,然后利用擬合函數對不同負載影響下的誤差量進行插值計算,得到對應負載的誤差補償量[7]。

3.2 誤差補償界面驗證實例

為了直觀地驗證誤差補償界面功能的有效性,本次實驗以1個質量為9.677 kg的工件為負載,具體步驟如下:

(1) 利用本文設計的試驗方案,在變載荷方盒內加入1塊質量為0.788 kg的砝碼,使負載總質量達到9.677 kg,試驗后對所得數據進行處理并記錄。

(2) 啟動誤差補償界面,在參數輸入界面選擇機器人型號FANUC M-10iAe、輸入末端載荷質量9.677 kg、選擇工作區間1及曲線擬合方式為三次多項式插值法,輸入完成后開始計算,記錄補償量數值。

綜上所述,得到試驗數據處理結果與誤差補償量的計算結果，見表4所列。

表4 試驗誤差量與誤差補償量對比

由表4可知,在X、Y、Z方向上試驗誤差量與誤差補償量之間的偏差分別為0.002 6、0.031 3、0.164 6mm,兩者的差異很小,可見該誤差補償界面計算的結果具有一定的可靠性。另外該誤差補償界面符合輸入簡單、顯示直觀的實際需求。用戶可以選擇在Matlab環境下保存所創建的圖形用戶界面,也可以通過mcc編譯生成可獨立運行的應用程序,這都將會拓展該誤差補償界面的應用場合。

4 結 論

本文基于特定的碼垛工作軌跡,將六自由度機器人動態誤差的研究轉化為對末端執行器定位精度的研究,重點分析了末端載荷的變化對機器人末端執行器絕對定位精度的影響。通過對比試驗結果和動力學仿真結果,說明根據剛柔耦合的動力學模型仿真得出的誤差結果是比較準確的,從而也驗證了動力學仿真對誤差變化的預測趨勢的正確性;應用驗證實例證明了本文設計的誤差補償界面可以對不同負載影響下的誤差進行插值計算,且結果具有一定的可靠性,可以為后續誤差補償提供參考,同時也為柔性生產條件下提高機器人精度提供了一種解決方案。

[1] 李定坤,葉聲華,任永杰,等.機器人定位精度標定技術的研究[J].計量學報,2007,28(3):224-227.

[2] 龔星如,沈建新,田威,等.工業機器人的絕對定位誤差模型及其補償算法[J].南京航空航天大學學報,2012,44(增刊1):60-64.

[3]PARKIW,LEEBJ,CHOSH,etal.Laser-basedkinematiccalibrationofrobotmanipulatorusingdifferentialkinematics[J].IEEE/ASMETransactionsonMechatronics,2012,17(6):1059-1067.

[4] 張利，潘承毅，劉征宇，等.差動驅動機器人的一種航跡推算定位方法[J].合肥工業大學學報(自然科學版), 2010, 33(11):1605-1608，1622.

[5]VERDONCKW.Experimentalrobotandpayloadidentificationwithapplicationtodynamictrajectorycompensation[D].Leuven:KatholiekeUniversityLeuven,2004.

[6] 王一,劉常杰,任永杰,等.工業坐標測量機器人定位誤差補償技術[J]. 機械工程學報,2011,47(15):31-36.

[7]ZHOUJ,NGUYENHN,KANGHJ.Simultaneousidentificationofjointcomplianceandkinematicparametersofindustrialrobots[J].ProceedingofIEEEInternationalJournalofPrecisionEngineeringandManufacturing,2014,15(11):2257-2264.

[8] 戴洪光.基于ADAMS平臺的柔性體仿真理論的若干研究[D].合肥:合肥工業大學,2008.

[9] 王魯平.串聯機器人多誤差因素影響下定位精度分析及其誤差補償[D].合肥:合肥工業大學,2015.

[10] 朱龍英,陸寶發,成磊,等.剛柔耦合機器人仿真及振動分析[J].中國工程機械學報,2015,13(2):120-123.

[11] 秦磊.工業機器人定位精度與腕部載荷關系研究[D].合肥:合肥工業大學,2014.

[12] 南小海.6R型工業機器人標定算法與實驗研究[D].武漢:華中科技大學,2008.

(責任編輯 胡亞敏)

Dynamic error analysis of 6-DOF serial robot

HOU Xiaoyu, ZHU Huabing, WANG Luping

(School of Mechanical Engineering, Hefei University of Technology, Hefei 230009, China)

Robot is affected by the factors such as load, link weight in the working process, of which links deformation makes the end actuator position error. In this paper, taking FANUC M-10iAe robot as the research object, the improvement of robot positioning accuracy is studied by using the method of simulation and experiment. The dynamic simulation in ADAMS environment is conducted, and the robot dynamic error caused by the variable load is analyzed. The tests using the self-designed measuring device and variable load box are done, and the result shows the accuracy of dynamic simulation. On the basis of the acquired error data, the error compensation interface based on human-computer interaction is designed and developed, and its effectiveness is validated by an example.

serial robot; flexibility; dynamic error; ADAMS simulation; load; error compensation interface

2015-08-27；

2015-12-31

合肥工業大學產學研校企合作資助項目(W2015JSKF0377)

侯小雨(1992-),男,安徽六安人,合肥工業大學碩士生; 朱華炳(1963-),男,安徽懷寧人,博士,合肥工業大學教授,博士生導師.

10.3969/j.issn.1003-5060.2017.03.003

TP242.2

A

1003-5060(2017)03-0299-05