一道綜合題中面積問題的四種解法
廣東省深圳市龍崗區(qū)龍崗中學(xué)(518116) 熊 猛 ●
一道綜合題中面積問題的四種解法
廣東省深圳市龍崗區(qū)龍崗中學(xué)(518116) 熊 猛 ●
采用點的整體設(shè)元,利用面積割補進行計算,或利用鉛錘高面積公式進行轉(zhuǎn)化,或利用平行線間的距離處處相等,進行三角形面積轉(zhuǎn)移,或利用點到直線的距離公式求高,再直接用三角形面積公式解決問題.
綜合題;面積問題;解法
∴A(-1,0),B(3,0),C(0,-3).設(shè)拋物線的解析式為y=a(x+1)(x-3),
∴ a(0-3)(0+1)=-3,∴a=-1,即y=x2-2x-3=(x-1)2-4.
(2)方法1:過點D作EF∥x軸,作PE⊥EF于點E,
BF⊥EF于點F.設(shè)P(m,m2-2m-3).
由(1)知,D(1,-4),B(3,0).
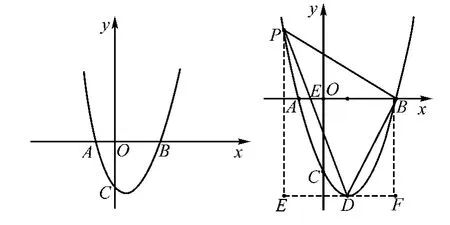
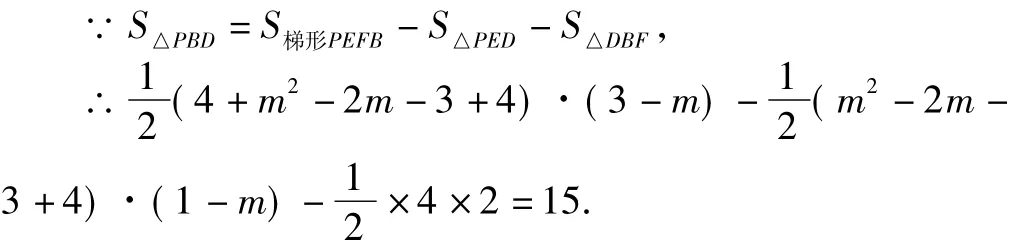
整理,得m2-4m-12=0,解得,m1=-2,m2=6(舍去).∴P(-2,5).
說明:本方法采用點的整體設(shè)元P(m,m2-2m-3),再利用面積割補進行計算,即 S△PBD=S梯形PEFB-S△PEDS△DBF,這是進行面積轉(zhuǎn)換最常用方法.
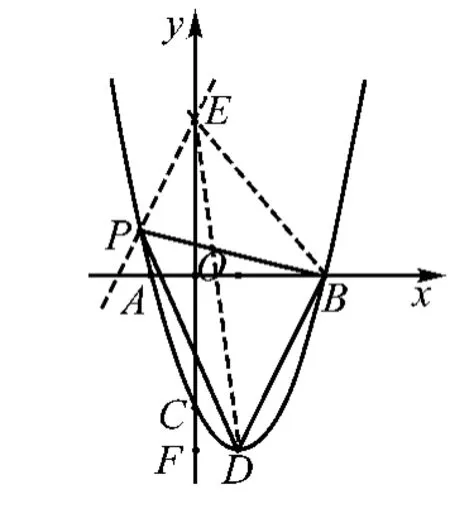
方法2:設(shè)P(m,m2-2m-3),由(1)知,D(1,-4),B(3,0).設(shè)直線PD: y = kx + b, 則解得
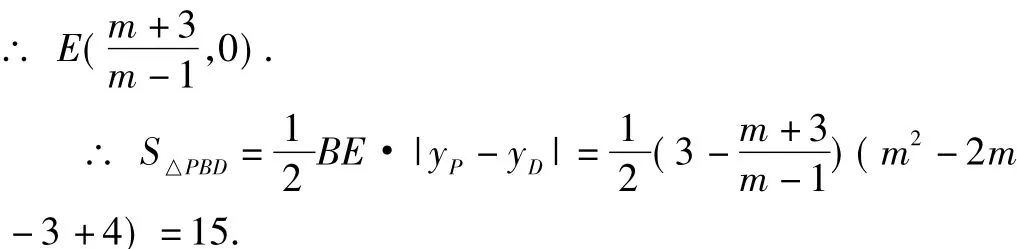
整理,得m2-4m-12=0.以下略.
說明:本方法運用求出直線PD與x軸交點坐標(biāo),再利用鉛錘高面積公式進行轉(zhuǎn)化.
方法3:設(shè)P(m,m2-2m-3),由(1)知,D(1,-4),B (3,0).∴直線BD:y=2x-6.
過點P作PE∥BD,交y軸于E,則S△PBD=S△BED.
設(shè)直線PE:y=2x+h,則有:2m+h=m2-2m-3,h= m2-4m-3,即直線PE:y=2x+m2-4m-3,則E(0,m2-4m-3).過點D作DF⊥y軸于F,則有:DF=1,OF=4,EF=a2-2a-3+4=a2-2a+1.
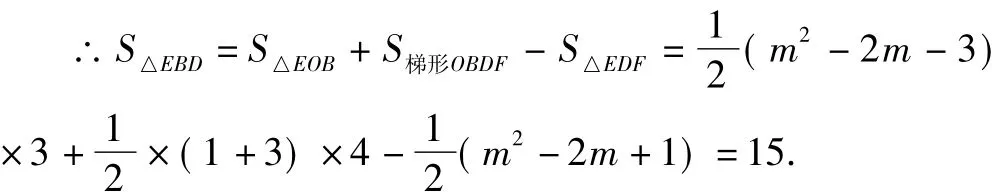
整理,得m2-4m-12=0.以下略.
說明:本方法利用平行線間的距離處處相等,將△PBD的面積轉(zhuǎn)化為△EBD的面積,再通過割補法進行轉(zhuǎn)換求解.
方法4:設(shè)P(m,m2-2m-3),由(1)知,D(1,-4),B (3,0).
∴直線BD:y=2x-6.
∴ 點P(m,m2-2m-3)到直線2x-y-6=0的距離為:
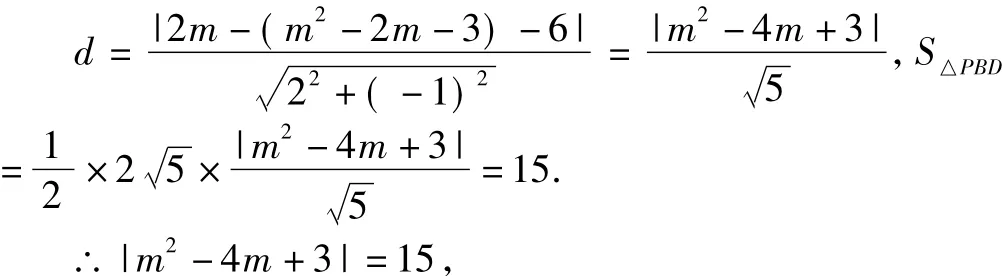
即m2-4m+3=15或m2-4m+3=-15(無解).
解得,m1=-2,m2=6(舍去).
∴P(-2,5).
說明:本題利用了高中數(shù)學(xué)知識——點到直線的距離公式,再直接用三角形面積公式解決問題.
以上幾種解法具有一定的通法指導(dǎo)意義,在解決有關(guān)面積問題的題目時,均可借鑒這些方法求解.
G632
B
1008-0333(2017)02-0021-01

