基于港口航運網拓撲結構的港口層次劃分
——以中國城市港口航運網為例

李電生 張騰飛 鐘丹陽

(中國海洋大學 經濟學院，山東 青島 266100)

基于港口航運網拓撲結構的港口層次劃分
——以中國城市港口航運網為例

李電生 張騰飛 鐘丹陽

(中國海洋大學 經濟學院，山東 青島 266100)

近年來，隨著中國經濟結構的調整，中國港口也進入了轉型調整階段，正從以往的外延式擴張向內涵式發展轉變，由原來的混沌式競爭向層次化布局過渡，港口的層次化發展是港口經濟發展的必然要求和發展趨勢，目前，國內外學者對于港口層次劃分的研究相當匱乏，尤其是缺少宏觀的港口航運網分析。為此，在傳統復雜網絡基礎上，構造了加權復雜網絡揭示港口航運網的拓撲結構特點，選取復雜網絡指標，通過聚類分析對網絡中的港口節點進行層次劃分，并以中國港口航運網為例進行實證分析，首先得出中國港口航運網具有“小世界”、無序性等特點，然后依據拓撲結構特點及各指標之間的相關性，選取指標將中國的港口劃分為四個層次，最后通過對結果進行分析，得出中國港口目前的發展狀況及未來的布局規劃。

港口層次劃分；中國港口航運網；加權復雜網絡；聚類分析

港口作為國際貿易得以實現的重要設施，受到沿海各城市的高度重視，改革開放以來，中國港口得到了快速發展，港口吞吐量由1978年的2.8億噸，增長到2015年接近百億噸，港口規模和數量都急劇增長，同時極大促進港口城市發展。然而，伴隨著中國經濟結構的調整，港口的獨立發展空間將受限，吞吐量的增速正逐年放緩，甚至出現負增長，港口到了從單個港口的獨立發展向港口間有層次的協同發展階段，因此，如何對港口層次進行合理劃分就成為目前港口轉型期的重要問題。

目前，國內外學者研究港口的文獻主要集中在港口群內競合研究、港口效率測度研究、單個港口吞吐量預測和港口分類等方面。例如，GI-tae、Peter等、[1-2]劉波和王憲明等多位國內外學者對港口群內部競爭和協調發展問題進行了研究；[3-4]Cullinane等、鐘銘等和龐瑞芝、李電生等對港口效率進行了研究。[5-8]Mak、Veerachai、Yi Xiao、蘇凌、許長新、陳秀瑛和蔣學煉等對單個港口的吞吐量進行了短期預測；[9-15]高鴻麗和鐘玉文等選取了多個港口指標及腹地城市指標通過聚類分析對長三角港口群及集裝箱港口的層次結構進行了研究。[16-17]上述文獻解決了單個港口規劃發展問題以及港口群的協同發展問題，但是這些研究都忽視了航線對港口的影響和作用。

港口航運網實質上是一個由港口節點和航線組成的復雜網絡。20世紀60年代，著名數學家Erdos和Renyi提出的ER隨機圖模型標志著復雜網絡理論的誕生，為更好描述現實網絡的拓撲結構特點，1998年Watts和Strogtz提出了小世界網絡模型，1999年Barabasi等構建的無標度網絡模型完善了復雜網絡理論。此后，胡一竑與蔡澤祥等將復雜網絡理論應用到了社會、信息、技術，以及生物等領域。[18-19]與此同時，廣大交通學者也對復雜網絡進行了大量的實證研究，田煒等用復雜網絡理論研究馬士基的海運網絡，發現網絡的小世界及無標度特性；[20]廖虹等用復雜網絡理論得出東北亞港口群具有小世界特性和無序性的結論；[21]Guimer等對美國航空線路網絡進行的分析發現美國航空網具有小世界特性、層級結構和“富人俱樂部”現象；[22]Sen等對印度鐵路網絡研究得出的鐵路網絡的“小世界網絡”性質。[23]

以上研究都是基于無權復雜網絡的視角分析航運網，在一定程度上揭示了航運網的拓撲結構特點，然而，港口之間并不是簡單的“有”和“無”的關系，就中遠集團而言，其在上海港與廣州港之間有9條航線，一個月有30多條船往來于兩個港口之間，而上海港與連云港港只有一條航線，一個月只有4條船往來兩個港口之間，這兩對港口之間的關系明顯不能用相同的1表示，因此，傳統的無權復雜網絡無法全面深刻地描述港口之間的緊密關系，本文用加權的復雜網絡研究中國的港口網絡。在中國港口國內航線沒有放開的條件下，中遠集團作為中國最大的航運公司，用其航線反映中國港口之間的聯系情況具有一定的代表性。因此，本文將港口作為節點，以中遠集團在兩個港口之間的航線數作為兩個港口之間聯系的權重構造加權復雜網絡。

一、加權復雜網絡模型

為描述加權網絡的結構特點，本文在無權復雜網絡各統計指標的基礎上引入度、點強度，平均最短路徑長度，聚集系數，匹配系數，網絡結構熵等加權復雜網絡的統計指標。

(一)度、點強度

節點度是節點非常重要的屬性，是對節點相互連接統計特性的最重要描述，節點i的度，定義為與該節點i直接相連的其他節點的數目，也就是0-1鄰接矩陣中第i列的數據和，即：

(1)

節點度在無權網絡中反映的是節點在網絡中的重要性，并且度作為節點的基本屬性，節點的其他統計指標都與其存在相關性。對于加權復雜網絡來說，節點點強度定義為與節點i相連的所有邊權之和也就是加權鄰接矩陣中第i列的數據和，即：

(2)

(二)權重分布的差異性

(三)平均最短路徑長度

在無權網絡中兩個節點i和節點j之間的距離dij定義為連接兩個節點的最短路徑上的邊數。對于本文所要研究的相似權加權網絡(權重越大，節點之間的聯系越大)的距離給出如下定義：把相似權加權網絡的最短路徑看作是時間成本，假設節點之間的距離為單位1，權重wij可以認為是從節點i到節點j的速度，這樣定義最短路徑長度為：

(3)

dij是從i到j所有路徑中權重倒數和最小。

整個網絡的平均最短路徑長度為：

(4)

(四)聚集系數

聚集系數也稱簇系數，是節點i的所有鄰居節點之間相互連接的平均權重，用以衡量網絡小集團結構程度，表示“朋友的朋友”之間的親密程度，是衡量網絡集聚特性和節點之間聯系密切程度的一個重要參數。

加權網絡的節點i聚集系數定義：

(5)

可以看出，以上公式在加權網絡退化為無權網絡時，公式(5)依然適用。整個網絡的聚集系數為：

(6)

Cw值越大表示整個網絡中節點之間的聯系越緊密，直接聯系的程度越大。

(五)匹配系數

匹配系數衡量的是網絡中點強度大的節點(影響力大的節點)之間更加傾向于聯系，還是點強度大的節點更傾向于聯系點強度小的節點，加權網絡的匹配系數為：

(7)

其中M為網絡中的總邊數，Si和Sj為一條連邊上的兩個端點的點強度。

(六)網絡結構熵

熵的概念最早提出是為了解決熱力學問題，后來融入了多個領域和學科，用于研究系統的穩定性和有序性。網絡結構熵是描述網絡異質性的一種統計指標。若加權網絡中每個節點的重要度mi定義為：

(8)

則網絡結構熵的定義為：

(9)

將網絡結構熵歸一化處理得到：

(10)

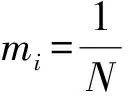
二、中國港口航運網絡的拓撲結構

港口航運網是以港口為節點，港口之間的航線為邊，不考慮港口節點的具體位置和邊的具體形態而形成的拓撲網絡，本文選取中國東部沿海30個港口組成的航運網絡為研究對象，以港口為節點，以中遠集團在兩港口之間的航線數為連邊權重構造加權復雜網絡模型。

(一)港口度及點強度

在港口航運網絡中，港口點強度是港口與其他港口之間的航線數目，是港口在整個網絡中集散能力的直接體現。通過構造的加權復雜網絡得到了中國港口航運網絡的港口度及點強度，見表1。

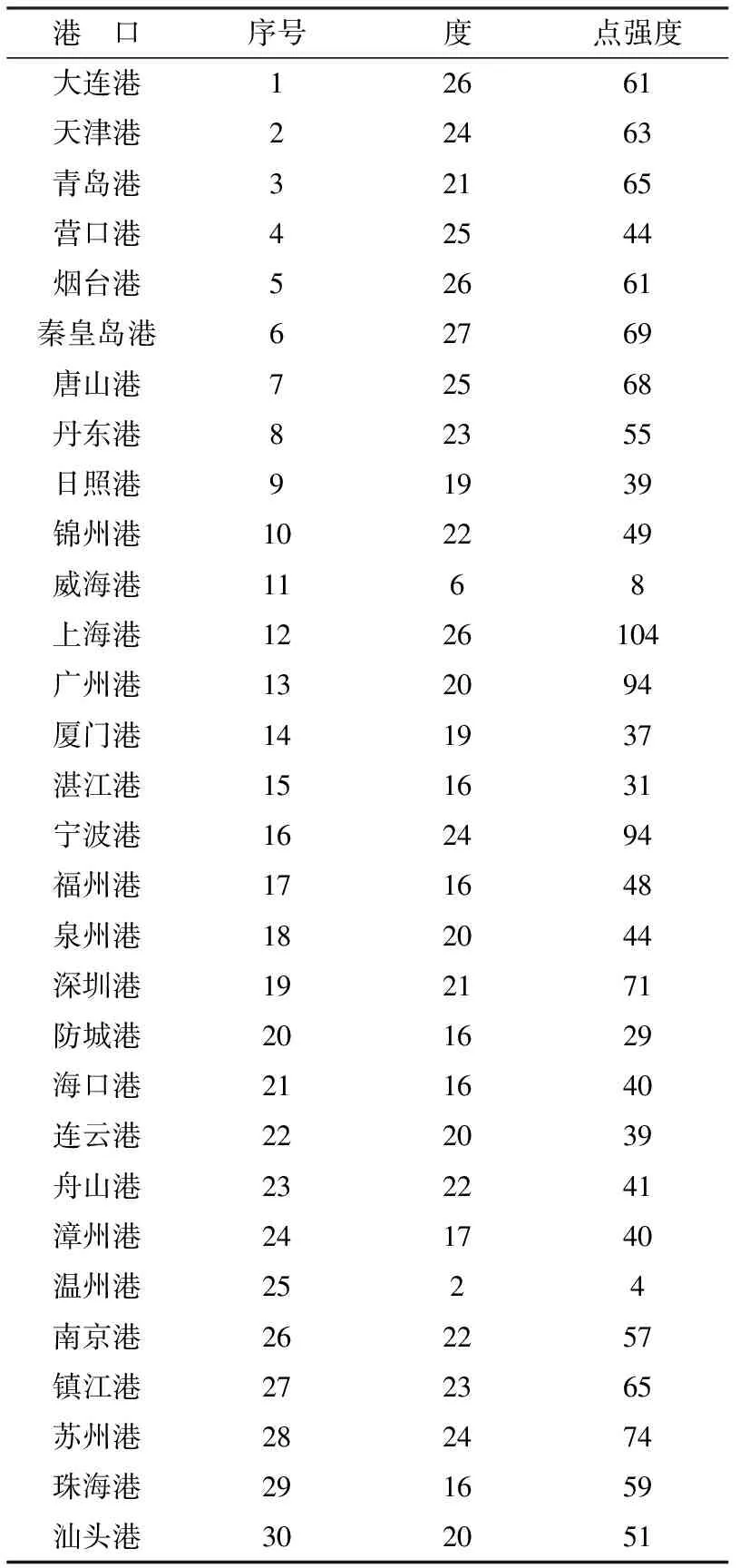
表1 度及點強度

表1中點強度較大的幾個港口上海港、廣州港、寧波港、深圳港、天津港、青島港及唐山港在2013年的世界港口吞吐量排名中全部位列前十，其他的點強度較大的港口(如秦皇島港、鎮江港、蘇州港)都曾在世界港口吞吐量排名中位列前十，這也從側面說明了在港口網絡中點強度大的港口其集散能力及影響力也相對較大。

從圖1中可以看出，港口的度分布及點強度分布都比較均勻，并不存在“絕對中心”的港口，只有威海港和溫州港的度值及點強度小于10，其他各港口均大于10，且港口的平均度為20.13，這說明港口網絡中的每個港口平均與其他20個港口都有聯系。

圖1 度與點強度散點圖

從圖2中可以看出，中國港口網絡與其他現實網絡一樣點強度與度之間也存在正相關關系：S(k)=1.42×k1.2，網絡中某一港口聯系的其他港口越多，即度值越大，該港口的點強度就越大，港口在網絡中的作用越大集散能力越好。

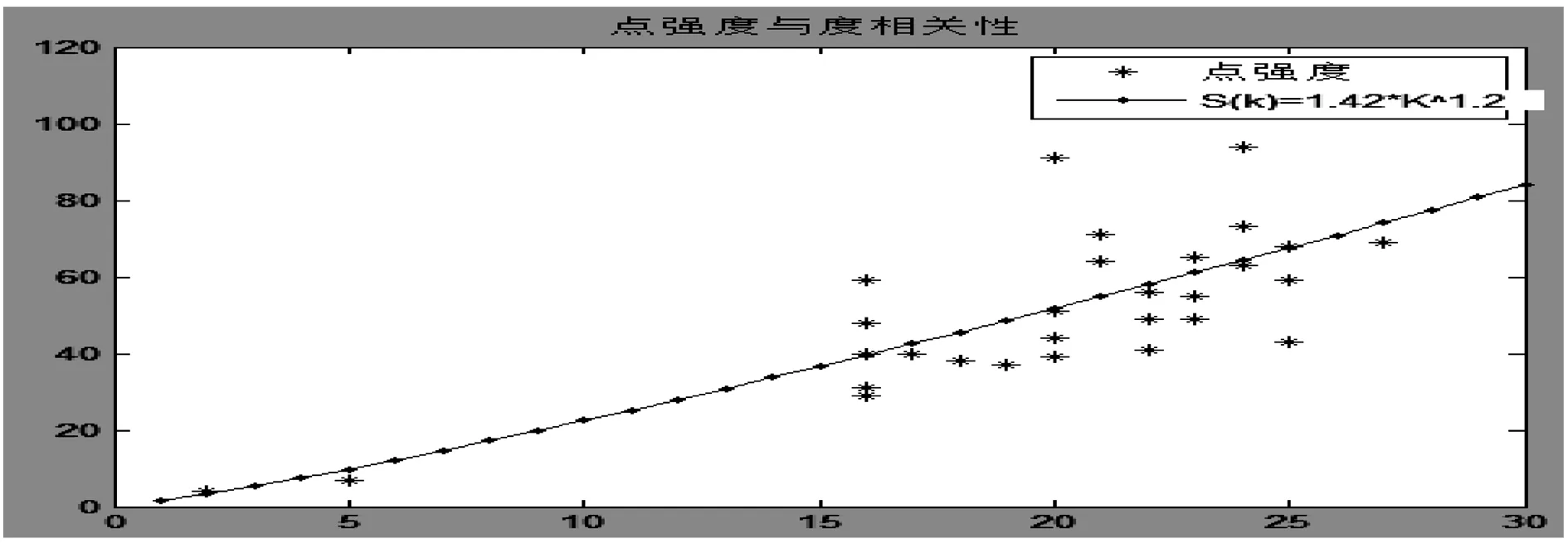
圖2 點強度與度相關性

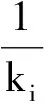
圖3 邊權離散分布

(二)港口航運網的平均路徑長度

在港口航運網絡中，兩個港口(i，j)之間的距離反映的是貨物由港口i到港口j的難易程度。港口i到其他港口距離的平均值則表示港口的中轉能力，整個網絡的平均路徑長度則表示港口網絡的通達程度。中國港口航運網絡的平均最短路徑長度為0.45，其中節點之間最短路徑長度最小值(廣州—上海和廣州—蘇州)為0.1，最大值(威海與溫州之間的路徑)為1.3，任意兩個港口之間進行信息交換的平均時間成本不到單位1，平均最短路徑長度較小，網絡效率比較高，網絡結構緊湊。

(三)港口航運網的聚集系數

港口節點的聚集系數是港口在局部范圍內的中心性的集中體現，而港口航運網的聚集系數則能反映出港口之間合作的緊密程度。中國港口航運網絡的聚集系數為2.03，網絡中港口i的任意兩個近鄰港口j、k之間平均以wjk=2.03的邊權聯系，港口j、k之間平均有兩條航線。而整個網絡的平均邊權約為1.7，由此可見，中國的港口航運網絡聚集系數較大，港口之間的相互聯系比較緊密。

(四)匹配系數

匹配系數能夠反映出中國港口相互合作的傾向性，通過公式(7)計算得到中國港口航運網的匹配系數r=0.59>0，航運網的同配性非常明顯，即網絡中點強度大的港口更傾向于連接點強度大的港口，而點強度大的港口與點強度小的港口之間的缺乏協同合作，港口之間的層次化合作程度較低。

(五)網絡結構熵

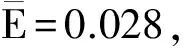
三、基于港口航運網拓撲結構的港口層次劃分

區分和確定港口層次是港口有序發展的重要因素，隨著港口的高速發展，傳統的港口分類方法已經不能準確地劃分出港口的層次結構。通過以上對港口網絡拓撲結構特點的研究發現中國港口的度值及點強度分布比較均勻，與港口直接相連的邊之間差異較小，港口之間的相互聯系也比較平衡且存在同質化聯系，因此依靠單一的指標無法對港口進行區分，本文在分析了各統計指標之間的相關性的基礎上，選取能夠全面反映港口特性的指標對中國港口進行層次劃分。

(一)指標選擇

點強度揭示了港口在航運網絡中的重要性及集散能力，是港口的基本屬性，港口節點的聚類系數是港口在局部范圍內的中心性的集中體現，港口節點的平均距離大小則反映了港口的中轉能力，港口吞吐量是港口規模大小的直接表現，是港口最重要的指標屬性，本文在對港口進行聚類時選用了2013年中國各港口的吞吐量。因此，以上四個指標可以較全面地反映港口的屬性。

(二)層次劃分結果

通過以上四個指標對中國東部沿海30個港口進行聚類得到圖4的結果。

圖4 港口聚類分析結果

由圖4可將中國的港口分為四個層次： {2 3 12 13 16 28}，{1 5 26 6 7 8 27 29 19 30}，{4 9 14 21 22 15 20 10 18 23 17 24}， {11 25}。第一層次港口包括青島港、天津港、上海港、廣州港、寧波港、蘇州港，第二層次港口包括大連港、煙臺港、南京港、秦皇島港、唐山港、丹東港、珠海港、深圳港、鎮江港、汕頭港，第三層次港口包括錦州港、泉州港、舟山港、福州港、漳州港、湛江港、防城港、營口港、日照港、廈門港、海口港、連云港。第四層次港口包括溫州港和威海港。以各個指標的平均值表示每個層次港口的基本情況，見表2。

表2 各個層次港口的平均值

表2可知，各層次之間的差距比較明顯，第一、第二層次的港口明顯優于第三、第四層次的，一般來說，吞吐量較大的港口其集散能力、中轉能力及中心性也相對較好。同屬于較高的層次，但是，日照港、營口港及連云港等港口依靠經濟發達的腹地，其吞吐量也較大，但是它們的集散能力、中轉能力和中心性較差，因此被歸入第三層次，而丹東港作為中國海岸線最北端的門戶，雖然吞吐量較少，但是其集散能力、中轉能力及中心性都相對較好，因此，被歸入第二層次。四個層次的港口相互之間聯系的平均邊權如表3。

表3 各層次港口聯系的平均邊權表

由表3可以看出，第一、第二層次的港口之間聯系較緊密，而高層次港口與低層次港口之間聯系較少，港口航運網絡還沒有形成樞紐港、支線港及喂給港格局，這是由于中國地方政府為了保護本地區利益，阻礙了其他港口與本地區港口之間的要素流動，港口更多的是關注自己的規模擴張，忽視了不同層次港口間的協同發展，但隨著中國經濟結構的深入調整，港口的獨立發展空間將受限，應積極發展市場經濟體制，形成以第一層次港口為樞紐港，第二層次港口為支線港，第三層次港口為喂給港的港口布局。其中，第二層次的大連港，由于其特殊的區位優勢，應作為樞紐港，第三層次的營口港因其巨大的吞吐量應作為支線港。具體地，中國應形成以大連港為樞紐，丹東港和營口港為支線港，錦州港為喂給港的遼寧沿海港口群；以天津港為樞紐，秦皇島為支線港，唐山港為喂給港的津冀沿海港口群；以青島港為樞紐，煙臺港為支線港，日照港為喂給港的山東沿海港口群；以上海港、寧波港及蘇州港為樞紐，南京港和鎮江港為支線港，連云港為喂給港的長三角港口群；以廣州港為樞紐港，珠海港和深圳港為支線港，汕頭港為喂給港的珠三角港口群。而東南沿海港口群及西南沿海港口群中的港口相對落后都屬于第三層次，需要進一步的發展。

四、結論

本文從宏觀的港口航運網的視角研究港口的層次布局問題，對港口的轉型發展具有重要的現實意義。通過對中國的港口航運網的實證分析可知，中國港口航運網跟許多現實網絡一樣具有較大的集聚系數，較小的平均最短路徑等小世界特性，沒有“絕對中心”的港口節點，信息傳輸效率較高，大港口之間的聯系較緊密，但是處于比較嚴重的無序惡性競爭狀態，港口之間同質化聯系較嚴重。通過選取復雜網絡指標將中國的港口分為四個層次，但不同層次的港口之間缺乏聯系與合作，港口的層次地位不夠明顯，處于混沌式發展狀態。地方政府應該放棄港口的部分產權，使港口發展更加市場化，不同層次的港口應該根據自身的實際情況進行合理的戰略定位，相互之間應加強合作和要素流動，從而形成以第一層次港口為樞紐港，第二層次為支線港，第三層次為喂給港的港口層次布局。

[1]GI-taeYeo,MichaelRoe,JohnDunwoody.EvaluatingthecompetitivenessofcontainerportsinKoreaandChina[J].TransportationResPartA:Policy&Practice, 2008.

[2]PeterW.deLangen,Evert-JanVisser.Collectiveactionregimesinseaportclusters:ThecaseofthelowerMississippiportcluster[J].JournalofTransportGeography, 2005, (13): 173-186.

[3] 劉波.省際邊界區港口競爭力比較及競合路徑研究——以連云港港與日照港為例[J].資源開發與市場,2010,(11):989-991.

[4] 王憲明.日本東京灣港口群的發展研究及啟示[J].國家行政學院學報,2008,(1):99-102.

[5]CullinaneK,WangT.A.comparisonofmathematicalprogrammingapproachestoestimatingcontainerportproduntionefficiency[J].Journalofproductivityanalysis, 2006(24):73-92.

[6] 鐘銘,呂媛媛.基于灰靶模型的港口效率評價[J].大連海事大學學報,2007,(6):130-132.

[7] 龐瑞芝.我國主要沿海港口的動態效率評價[J].經濟研究,2006,(6):92-100.

[8] 李電生,員麗芬.港口群物流系統效率測度——基于多子系統模糊DEA模型分析[J].北京交通大學學報(社會科學版),2010,9(2):42-47.

[9]K.L.Mak,D.H.Yang.ForecastingHongKong'scontainerthroughputwithapproximateleastsquaressupportvectormachines[J].ProceedingsoftheWorldCongressonEngineering, 2007,1.

[10]VeerachaiGosasang,WatcharaveeChandraprakaikul,SupapornKiattisin.AnapplicationofNeuralNetworksforforecastingcontainerthroughputatbangkokport[J].ProceedingsoftheWorldCongressonEngineering, 2010,1.

[11]YiXiao,JinXiao,ShouyangWang.Ahybridforecastingmodelfornon-stationarytimeseries:Anapplicationtocontainerthroughputprediction[J].InternationalJournalofKnowledgeandSystemsScience, 2012, 3(2): 67-82.

[12] 蘇凌.基于徑向基函數神經網絡的港口吞吐量預測研究[D].上海海事大學,2006.

[13] 許長新,嚴以新,張萍.基于系統動力學的港口吞吐量預測模型[J].水云工程,2006,(5):26-28.

[14] 陳秀瑛,古浩.灰色線性回歸模型在港口吞吐量預測中的應用[J].水運工程,2010,(5):89-92.

[15] 蔣學煉,吳永強,史艷嬌.港口吞吐量預測的混合算法實證研究[J].中國港口建設,2009,(2):7-11.

[16] 高鴻麗,顧亞竹.聚類分析在長江三角洲地區港口分類中的應用[J].中國航海,2003,(4):26-30.

[17] 鐘玉文.集裝箱港口分類探討[J].中國水運(理論版),2006,(6):41-42.

[18] 胡一竑,朱冰心.復雜網絡理論在供應鏈管理中的應用[J].物流科技,2007,(9):100-103.

[19] 蔡澤祥,王星華,任曉娜.復雜網絡理論及其在電力系統中的應用研究綜述[J].電網技術,2012,36(11):114-121.

[20] 田煒,鄧貴仕,武佩劍,等.世界航運網絡復雜性分析[J].大連理工大學學報,2007,47(4):605-609.

[21] 廖虹,王杰.復雜網絡下的東北亞港口群空間網絡演化研究[D].大連海事大學,2012.

[22]Guimer.Modelingtheworld-wideairportnetwork[J].EurPhysJ:B, 2004,38: 381-385.

[23]SenP,DasguptaP,ChatterjeeA,etal.Small-worldpropertiesoftheIndianrailwaynetwork[J].PhysRev:E, 2003,67: 036106.

責任編輯：王明舜

Port Hierarchy Partition Based on the Topological Structure of Port Shipping Network——An Empirical Study on Ports of Chinese Cities and Shipping Network

Li Diansheng Zhang Tengfei Zhong Danyang

(College of Economics, Ocean University of China, Qingdao 266100, China)

In recent years, the competition among Chinese ports has changed from extensive expansion to intensive development, from original chaotic competitive state to hierarchical layout, with the adjustment of Chinese economic structure. Hierarchical port development is the inevitable requirement of port economy and development trend. At present, domestic and foreign research on the port hierarchy is rare, especially macro analysis of port shipping network. Therefore, bases on traditional complex network, a weighted complex network to reveal characteristics of port shipping network's topology structure has been constructed; gradation of ports by selecting complex network indicators has been classified. The paper takes Chinese ports and shipping networks as an example for empirical analysis, and firstly, finds the characteristics of Chinese port shipping network's topology structure; and then, based on the characteristics of the topology structure and the correlation between the various indicators, the paper selects indicators to divide Chinese ports into four levels. Finally, through the analysis of the results, the paper concludes the current development of China's ports and future layout planning.

port hierarchy partition; Chinese ports and shipping network; weighted complex network; cluster analysis

2016-11-18

國家社會科學基金資助項目“基于市場配置資源的我國沿海港口群轉型升級研究”(15BJL103)

李電生(1966- )，男，河北石家莊人，中國海洋大學經濟學院副教授，主要從事港口規劃與管理研究。

F127

A

1672-335X(2017)02-0085-06