馬爾科夫切換型時滯系統(tǒng)的穩(wěn)定性

葉志勇，潘素英，張 華，2

(1.重慶理工大學(xué) 理學(xué)院， 重慶 400054; 2.銅仁學(xué)院 大數(shù)據(jù)學(xué)院， 貴州 銅仁 554300)

?

馬爾科夫切換型時滯系統(tǒng)的穩(wěn)定性

葉志勇1，潘素英1，張 華1，2

(1.重慶理工大學(xué) 理學(xué)院， 重慶 400054; 2.銅仁學(xué)院 大數(shù)據(jù)學(xué)院， 貴州 銅仁 554300)

馬爾科夫切換型時滯系統(tǒng)是能很好地描述具有隨機(jī)性同時又具有時滯的一類系統(tǒng)，而穩(wěn)定性是其研究的基礎(chǔ)。通過選取合適的Lyapunov-Krasovskii泛函，利用線性矩陣不等式和Schur補(bǔ)引理得到了依賴于時滯的穩(wěn)定性判據(jù)，理論上說明了所考慮系統(tǒng)在足夠小的時滯條件下可以達(dá)到漸近穩(wěn)定。最后通過Matlab LMIs Toolbox可以找到可行的矩陣解，并且借助Matlab LMIs Toolbox進(jìn)行了數(shù)值仿真，說明了所得結(jié)論的有效性。

時滯；隨機(jī)系統(tǒng)；Brownian運(yùn)動；馬爾科夫切換

時滯現(xiàn)象是造成系統(tǒng)不穩(wěn)定、降低系統(tǒng)性能的主要因素之一，它廣泛存在于各種工程系統(tǒng)中，進(jìn)而使時滯系統(tǒng)受到大量關(guān)注，并且取得了豐碩的研究成果[1-3]。對于時滯系統(tǒng)的研究已深入各分支，比如時滯系統(tǒng)的時滯相關(guān)與否、時滯相關(guān)的穩(wěn)定性分析與設(shè)計、參數(shù)識別等。

在實(shí)際的物理系統(tǒng)中，存在著許多的噪聲和不確定性，而噪聲和不確定性的干擾使得原有系統(tǒng)的性質(zhì)被破壞。為了更好地刻畫系統(tǒng)的內(nèi)在性質(zhì)，同時更準(zhǔn)確、深入地對實(shí)際物理系統(tǒng)進(jìn)行描述，研究中引入隨機(jī)系統(tǒng)。高斯噪聲是由Brown運(yùn)動引起的干擾，而在實(shí)際生活中，系統(tǒng)除了受高斯噪聲的干擾外，還受諸多其他噪聲的干擾，如Possion噪聲等。

在實(shí)際工程系統(tǒng)中，由于隨機(jī)錯誤、不可預(yù)測的事件、互聯(lián)子系統(tǒng)的變化等會引起系統(tǒng)參數(shù)的改變，而馬爾科夫切換型隨機(jī)系統(tǒng)就能很好地描述這種現(xiàn)象。馬爾科夫切換型隨機(jī)系統(tǒng)同時包含離散和連續(xù)狀態(tài)，它可以對本身具有多模態(tài)性質(zhì)的動態(tài)系統(tǒng)和為了提高系統(tǒng)的性能而采取多控制器切換的智能控制系統(tǒng)進(jìn)行很好的描述，因而馬爾科夫切換型隨機(jī)系統(tǒng)理論和相應(yīng)的控制方法在飛行器控制、電力系統(tǒng)、網(wǎng)絡(luò)通信、無線伺服控制等諸多領(lǐng)域都有研究。毛學(xué)榮和袁成桂合著了第1本關(guān)于具有Markov切換的隨機(jī)系統(tǒng)專著[1]。基于該文獻(xiàn)的研究成果，Markov切換的隨機(jī)系統(tǒng)的能控性、魯棒性、穩(wěn)定性等相關(guān)理論取得了相應(yīng)的進(jìn)展[4-9]。對于馬爾科夫切換型隨機(jī)系統(tǒng)的穩(wěn)定性的研究有許多的相關(guān)文獻(xiàn)，包含各種不同的穩(wěn)定性(比如指數(shù)穩(wěn)定、隨機(jī)穩(wěn)定、幾乎必然指數(shù)穩(wěn)定等)研究。本文主要考慮：對于馬爾科夫切換型隨機(jī)時滯系統(tǒng)，在給定的初始擾動下，當(dāng)所含時滯足夠小時，系統(tǒng)仍然能夠達(dá)到穩(wěn)定狀態(tài)。為了實(shí)現(xiàn)系統(tǒng)的穩(wěn)定，選取一個Lyapunov-Krasovskii泛函，再根據(jù)其判據(jù)得到想要的結(jié)果。

1 基礎(chǔ)知識和模型建立

已知對于一個含單時滯τ的時滯系統(tǒng)，如果所考慮的系統(tǒng)對所有τ≥0都滿足該系統(tǒng)的穩(wěn)定性判據(jù)，則稱該系統(tǒng)是時滯無關(guān)的。如果穩(wěn)定性準(zhǔn)則與時滯τ是無關(guān)的，也就是所得的穩(wěn)定性準(zhǔn)則中不出現(xiàn)τ，則稱該穩(wěn)定性準(zhǔn)則是時滯無關(guān)穩(wěn)定性條件。如一個穩(wěn)定性準(zhǔn)則與時滯τ相關(guān)，即穩(wěn)定性準(zhǔn)則中出現(xiàn)τ，則稱該穩(wěn)定條件是時滯相關(guān)穩(wěn)定條件。

令(Ω,F,{Ft},P)是一個完備的概率空間，濾子{Ft}t>0滿足通常條件(即{Ft}t>0右連續(xù)，且F0包含所有概率為零的集合)。

所考慮的模型描述如下：

(1)

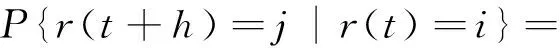
引理1(Schur補(bǔ))[10]對于給定在Rm的矩陣Q(x)=QT(x)，R(x)=RT(x)，以及S(x)，線性矩陣不等式(LMI)

等價于R(x)>0,Q(x)-S(x)R-1(x)ST(x)>0或者Q(x)>0,R(x)-S(x)Q-1(x)ST(x)>0。

2 主要定理

本文將對系統(tǒng)(1)的穩(wěn)定性進(jìn)行分析，其詳細(xì)結(jié)果由定理1給出。

(2)

(3)

其中：

則系統(tǒng)(1)是漸近穩(wěn)定的。

證明 為了得到系統(tǒng)(1)的穩(wěn)定性，選取如下的Lyapunov-Krasovskii泛函：

其中：

V1(x(t),r(t),t)=xT(t)P(r(t))x(t)

且PT(r(t))=P(r(t))>0,QT(r(t))=Q(r(t))>0,RT=R>0。

為了敘述方便，不妨記r(t)=i,i∈S。當(dāng)外部擾動B(t)=0時，可以求得V(x(t),r(t),t)的如下無窮小算子：

LV2(x(t),r(t),t)+LV3(x(t)

LV2(x(t),r(t),t)=xT(t)Qix(t)-xT(t-τ)Qix(t-τ)+

因此，根據(jù)不等式(3)，LV(x(t),r(t),t)能夠被放大為：

LV(x(t),r(t),t)≤2xT(t)PiAix(t)+

2xT(t)PiBix(t-τ)+

xT(t-τ)Qix(t-τ)+τxT(t)Rx(t)=

xT(t)Ξ1ix(t)+2xT(t)PiBix(t-τ)-

xT(t-τ)Qix(t-τ)

這里

不過這場“抵制塑料吸管”的社會運(yùn)動，并沒有得到所有人的響應(yīng)，甚至遭到了某些群體的反對和質(zhì)疑。比如，有殘疾人權(quán)益群體表示，塑料吸管，特別是可彎曲的那種，是某些殘障人士不可或缺的生活輔助用品。

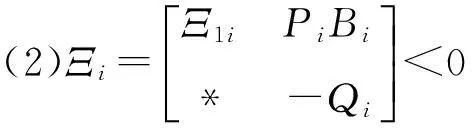
3 實(shí)驗(yàn)仿真

對于系統(tǒng)(1)

Cr(t)x(t)dB(t)

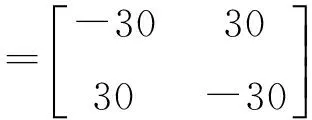
根據(jù)定理1,借助Matlab求得可行的解為：

根據(jù)實(shí)驗(yàn)的仿真結(jié)果，利用Matlab繪制隨機(jī)切換和狀態(tài)響應(yīng)圖，見圖1～2。

圖1 隨機(jī)切換

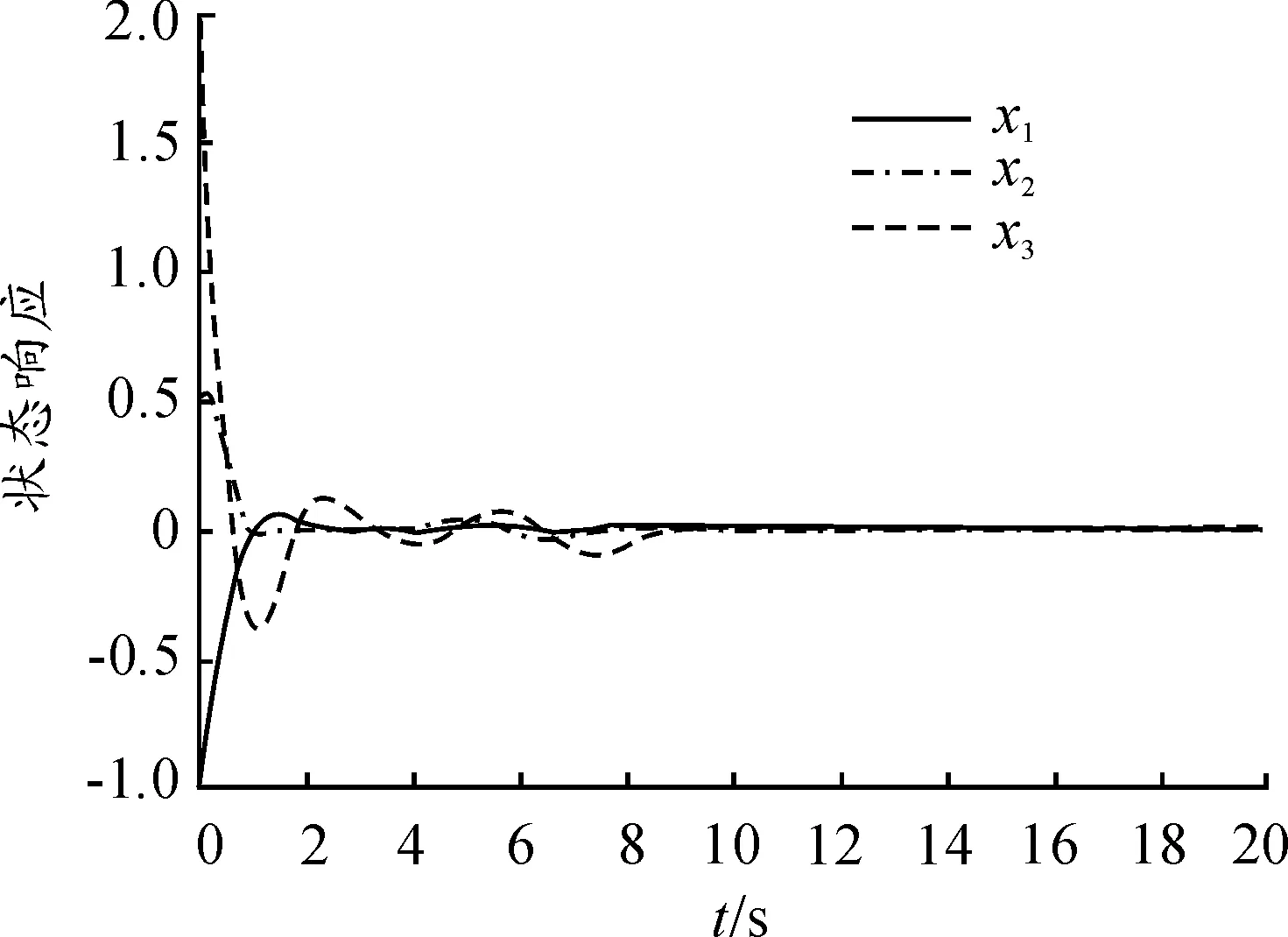
圖2 狀態(tài)響應(yīng)

圖1表示在r0=2的初始條件下的馬爾科夫鏈切換的一種可能狀態(tài)。圖2顯示的是系統(tǒng)在給定初值x0=(-1;0.5;2)和時滯τ=0.5條件下的狀態(tài)響應(yīng)。可以看到：所考慮系統(tǒng)在相應(yīng)的條件下最終可以實(shí)現(xiàn)漸近穩(wěn)定。

4 結(jié)束語

本文基于馬爾科夫切換的時滯系統(tǒng)，借助依賴于參數(shù)時滯的Lyapunov-Krasovskii泛函的方法，得到了所考慮系統(tǒng)漸近穩(wěn)定地依賴于時滯的充分條件。此方法借助于Schur補(bǔ)引理，進(jìn)而將系統(tǒng)的穩(wěn)定性問題轉(zhuǎn)化為線性矩陣不等式的可行性問題，最后借助軟件Matlab的LMIstoolbox找到不等式可行的解，且驗(yàn)證了結(jié)果的有效性。

[1]MAOX,YUANC.StochasticdifferentialequationswithMarkovianswitching[M].London:ImperialCollegePress,2006.

[2]XUS,LAMJ.Onequivalenceandefficiencyofcertainstabilitycriteriafortime-delaysystems[J].IEEETransactionsonAutomaticControl,2007,52(1):95-101.

[3] 劉蕾,羅賓,韓存武,等.線性時滯系統(tǒng)的穩(wěn)定性分析與控制[J].計算機(jī)仿真,2015,32(8):327-331.

[4]SHIP,ZHANGY,CHADLIM,etal.MixedH-infinityandpassivefilteringfordiscretefuzzyneuralnetworkswithstochasticjumpsandtimedelays[J].IEEEtransactionsonneuralnetworksandlearningsystems,2016,27(4):903-909.

[5]YANGJ,ZHOUW,PENGS,etal.SynchronizationofdelayedneuralnetworkswithLévynoiseandMarkovianswitchingviasampleddata[J].NonlinearDynamics,2015,81(3):1-11.

[6]ZHOUWN,TONGDB,GAOY,etal.Modeanddelay-dependentadaptiveexponentialsynchronizationinpthmomentforstochasticdelayedneuralnetworkswithMarkovianswitching[J].IEEETransactionsonNeuralNetworks&LearningSystems,2012,23(4):662-668.

[7]WANGZD,LIUYR,LIUXH.ExponentialStabilizationofaClassofStochasticSystemWithMarkovianJumpParametersandMode-DependentMixedTime-Delays[J].AutomaticControlIEEETransactionson,2010,55(7):1656-1662.

[8]CHENWH,ZHONGJC,ZHENGWX.Delay-independentstabilizationofaclassoftime-delaysystemsviaperiodicallyintermittentcontrol[J].Automatica,2016,71:89-97.

[9]CHENWH,ZHENGWX.Delay-IndependentMinimumDwellTimeforExponentialStabilityofUncertainSwitchedDelaySystems[J].AutomaticControlIEEETransactionson,2010,55(10):2406-2413.

[10]BOYDS,GHAOUILE,FERONE.LinearMatrixIneq-ualityinsystemandcontroltheory[M].Philadelphia:AIAM,1994.

(責(zé)任編輯 陳 艷)

Stability of Markov Switching Delay Systems

YE Zhi-yong1, PAN Su-ying1, ZHANG Hua1,2

(1.College of Science, Chongqing University of Technology, Chongqing 400054, China;2.Big Data Institute, Tongren University, Tongren 554300, China)

Markov switching delay system is a kind of systems which can be well described as the system with random and time delay. The stability is the foundation of its research. By choosing a appropriate Lyapunov-Krasovskii functional, using linear matrix inequality and Schur lemma, the stability criteria dependent on the sufficient small delay for the considered system can achieve asymptotic stability. Finally, the feasible matrix solution can be found by LMIs Toolbox Matlab, and the numerical simulation was designed by means of LMIs Toolbox Matlab, which shows the effectiveness of the conclusion.

time-delay; stochastic system; Brownian motion; Markov switching

2016-11-16

國家自然科學(xué)基金資助項目(61364006)；重慶市教委科學(xué)技術(shù)項目(KJ1500915)；重慶理工大學(xué)科研項目(2013ZD22)

葉志勇(1966一 )，男，四川富順人，博士，教授，主要從事微分方程與動力系統(tǒng)研究，E-mail:yezy@cqut.edu.cn。

葉志勇，潘素英，張華.馬爾科夫切換型時滯系統(tǒng)的穩(wěn)定性[J].重慶理工大學(xué)學(xué)報(自然科學(xué))，2017(4):141-144.

format：YE Zhi-yong, PAN Su-ying, ZHANG Hua.Stability of Markov Switching Delay Systems[J].Journal of Chongqing University of Technology(Natural Science)，2017(4):141-144.

10.3969/j.issn.1674-8425(z).2017.04.023

O231.1

A

1674-8425(2017)04-0141-04