基于交易費用的信息控制投資組合模型
李阿娜,孫華東,景永強
(中北大學 理學院, 太原 030051)
?
基于交易費用的信息控制投資組合模型
李阿娜,孫華東,景永強
(中北大學 理學院, 太原 030051)
通過將信息風險函數引入投資組合模型,構建更加符合實際的帶交易費用的信息控制模型,與傳統的帶交易費用的投資組合模型進行了比較,并且通過數學規劃中的罰函數算法對模型進行求解,完成了模型的實證分析,驗證了該模型和罰函數算法的有效性。
交易費用;數學模型;罰函數;信息控制;組合投資
從1952年馬克維茨針對組合投資問題提出了均值-方差模型以來[1],最優化在組合投資問題中的應用已受到越來越多的研究人員及投資者的關注[2-8]。投資組合的組合優化模型可以降低投資中的非系統風險,達到分散風險的目的,然而針對具體的非系統風險構建的投資組合模型還較少[8-10]。因此,本文將非系統風險中的信息風險函數引入投資組合優化模型中,構建了帶交易費用的信息控制投資組合優化模型,提出了改進的罰函數算法,并對模型進行求解,與傳統的帶交易費用的投資組合模型進行比較,驗證了模型和算法的有效性。
1 帶交易費用的投資組合模型
假設投資組合模型中的收益函數用線性函數來表示,加入交易費用函數后投資組合的收益比原來的投資組合的收益有所降低,由于資產交易過程中需要使用一部分收益用于支付交易傭金,則投資組合的收益函數表示為
g(x,r)=xTr-c(x)
其中:x表示資產的投資權重的向量;r表示資產收益率向量。
由于交易費用是從投資者的資本總額中扣除的,因此總的資本額的約束條件也發生了相應的變化,新的投資總額的約束條件可表示為
基于交易費用函數的投資組合問題可通過如下模型表示:
其中:向量x表示引入交易費用函數模型的資產配置權重;向量r表示每種資產的收益率;E(R)表示引入交易費用函數模型投資組合的期望收益,wi為第i種風險資產的單位交易費用; c(x)表示投資組合的交易費用函數; ck(xk)表示資產k所需交納的費用。帶交易費用的投資組合模型是含有絕對值函數的數學規劃模型,由于絕對值函數是非光滑的,因此該模型為非光滑的二次數學規劃模型。
2 帶交易費用的信息控制投資組合模型
由于信息控制函數的變化量可導致投資者對投資組合進行相應的調整,進而影響整個組合投資的收益率,因此信息控制函數對資產收益率的影響可表示為
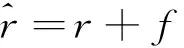
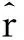
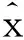
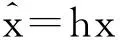
則總的資本額的約束條件也發生了相應的變化,引入信息函數后的投資總額的約束條件可表示為
帶交易費用的信息控制投資組合模型可表示為:
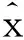
3 模型的求解
由于交易費用函數中含有非交易的絕對值函數,則帶交易費用的信息控制投資組合模型為非光滑的二次數學規劃模型,為模型的求解帶來困難。針對非光滑的交易費用函數,可通過變換進行求解。
針對絕對值函數作以下變換,令
那么uk滿足:
因此,帶有交易費用函數的信息控制投資組合模型可轉換為
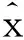
該模型為二次規劃模型,本文通過罰函數算法進行求解。首先通過罰函數將帶約束的模型轉化為無約束的非線性規劃模型,然后通過無約束規劃問題的相應求解方法進行該模型的求解。
定義1 稱
為帶交易費用的信息控制投資組合模型的罰函數模型,
為上述的帶紅利的信息控制投資組合優化模型的罰函數,σ>0為罰因子,其中
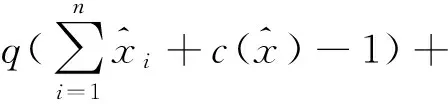
罰函數算法步驟如下:
步驟1 選定變量的初始點為x0;選取罰函數的初始罰因子σ1>0(可取σ1=1),罰因子的放大系數c>1(可取c=10);置k=1。
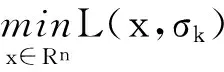
步驟3 若σkQ(x)<ε,則xk就是所要求的最優解,停止;否則轉下一步。
步驟4 置σk+1=cσk;k=k+1,轉步驟2。
因為懲罰項的特點,當k趨向于無窮大時,隨著σk的不斷增大,對每個不可行點的懲罰σkQ(x) 也將不斷的增大并且趨向于無窮。所以,在對應于σk的約束極小化問題的最優解xk處,σkQ(x)的值應該是不斷地減小,從而保證xk逐步趨向于可行并最終得到上述問題的最優解。
4 實證分析
對本文提出的帶有交易費用函數的信息控制投資組合模型及其相應的罰函數算法進行數值實驗和實證分析。依據行業背景和公司的成長性分析,選取大秦鐵路(601006)、申能股份(600642)、青島海爾(600690)、豐樂種業(000713)、華東醫藥(000963)、成霖股份(002047)、華神集團(000790)、如意集團(000626)8只股票進行實證研究。 收集這8只股票從2010年1月—2015年12月的月平均收益率(數據來源于www.ytarsc.com),通過每種資產的歷史資產收益的數據計算每只股票收益率的均值和方差。如表1所示,采用蒙特卡羅法進行每種資產收益率的數據模擬[11-12]。本文選取的模擬數據的樣本數為30 000,模型中參數的初始化數據如表2所示。

表1 資產的期望與方差

表2 模型參數的初始化數據
1) 通過設定不同的投資者預期收益率,應用Matlab軟件對帶有交易費用的投資組合模型進行求解,計算結果如表3、表4和圖1所示。將帶交易費用的投資組合模型簡記為CP模型。 表3為在投資者的預期收益率為10%時,通過計算得出的帶交易費的模型的計算結果。表3表明在預期收益率一定時,通過配置風險較小、收益率較高的資產可達到投資組合的風險最小化。表4為帶交易費用的模型在不同預期收益率下得到的投資組合的目標值,即風險值。 由表4和圖1可知:隨著預期收益率的增大,其相應的目標函數值也增大,符合收益越大風險越大的投資規律。表3、表4表明了本文提出的模型和算法的有效性,為投資者提供了一定的決策性參考。
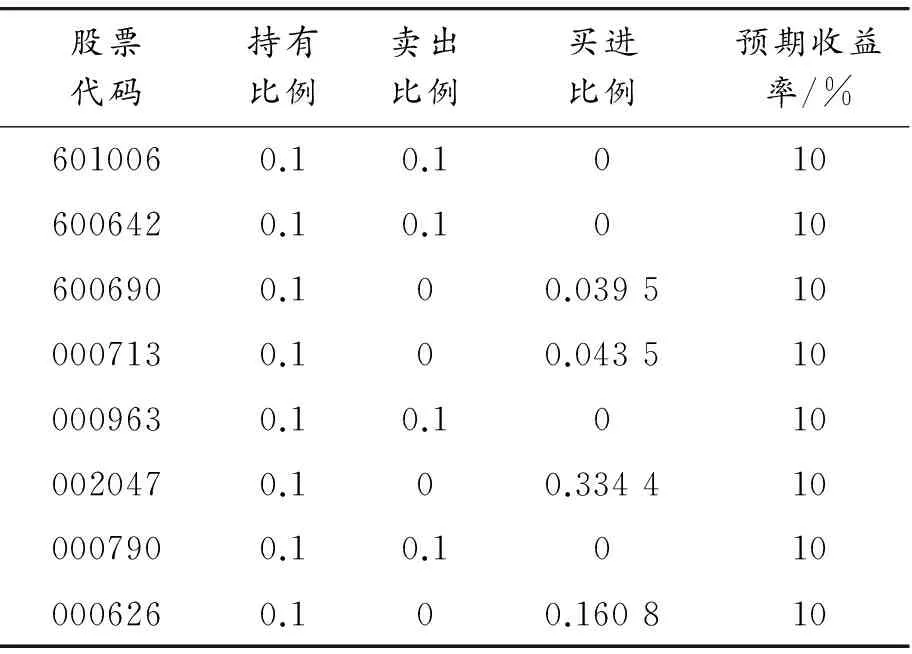
表3 帶交易費的投資組合模型的計算結果
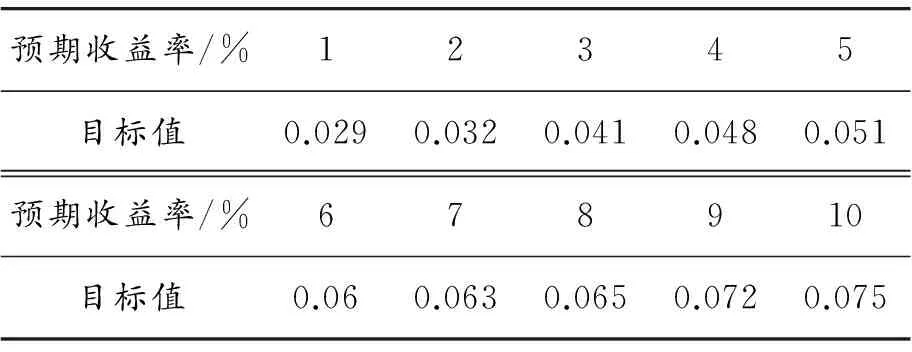
表4 不同預期收益率下CP模型的計算結果
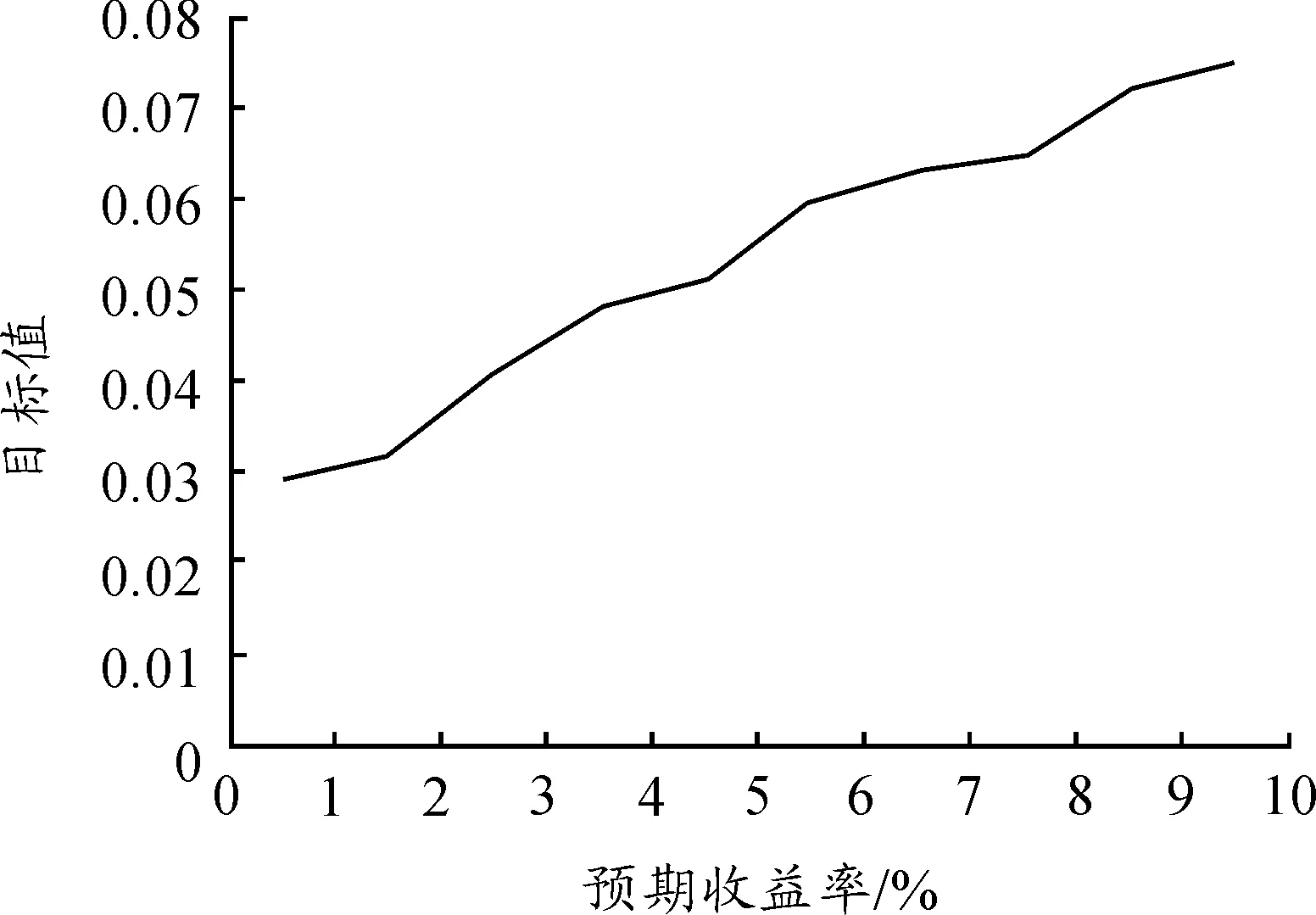
圖1 不同預期收益率下CP模型的計算結果
2) 設定不同的投資者的預期收益率,通過Matlab軟件對帶交易費用的信息控制投資組合優化模型進行計算,結果如表5、表6和圖2所示。將帶紅利的信息控制投資組合模型簡記為CIP模型。
表5表示在投資者的預期收益率為10%時,通過Matlab計算的帶交易費用的信息控制投資組合優化模型的結果,驗證了該模型及其相應的罰函數算法的有效性。通過對比表3發現:帶交易費用的信息控制模型具有較低的投資組合風險。投資者將帶有不利信息的資產賣出,增持帶有利信息的資產,從而獲得風險更低的投資組合。通過設定不同的預期收益率,利用帶交易費用的信息控制模型得到其相應的風險值,如表6和圖2所示。表6表明:預期收益率越高,資產組合的風險越大,符合高風險高收益,低風險低收益的投資規律。通過對比表4和表6,發現帶交易費用的信息控制模型更符合實際,能更好地為投資者提供投資決策。
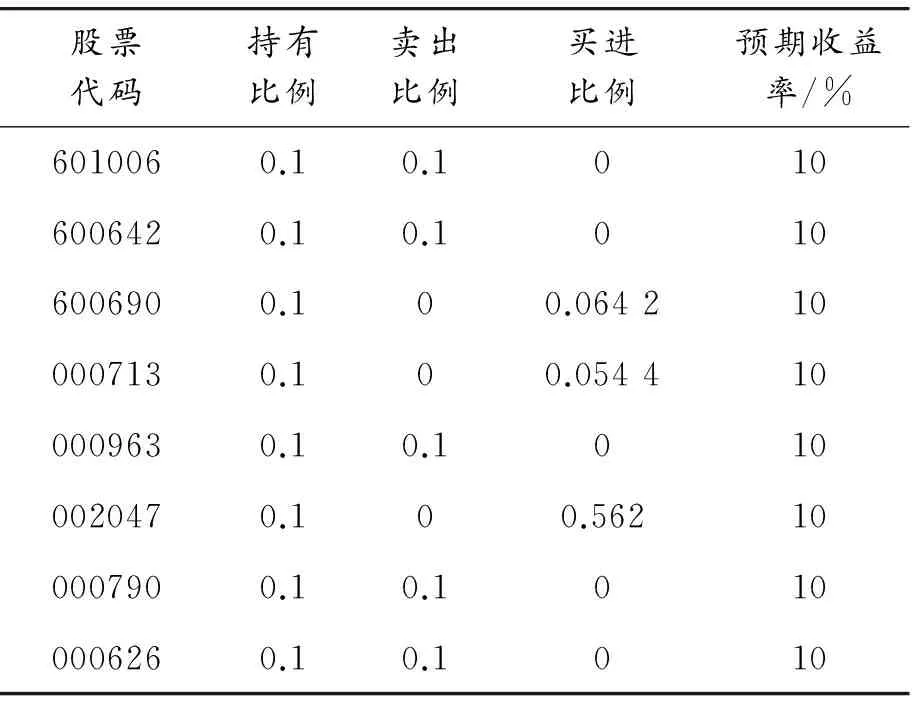
表5 帶交易費用的信息控制投資組合
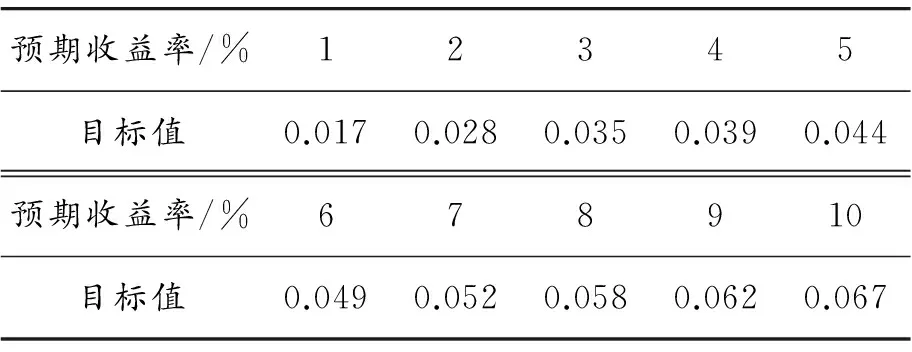
表6 不同的預期收益率下CIP模型的計算結果
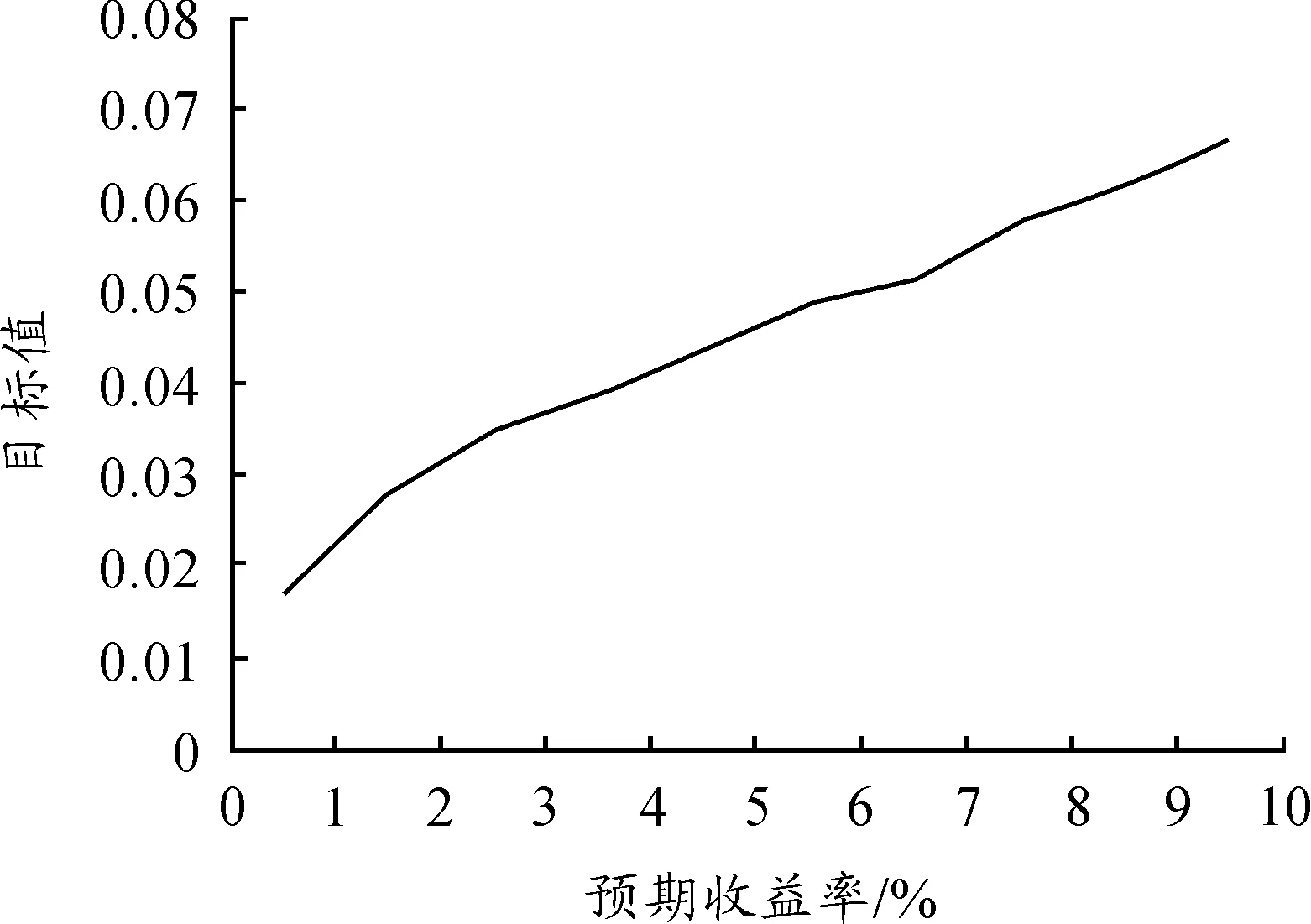
圖2 不同的預期收益率下CIP模型的計算結果
3) 通過設定不同的交易費用比例,應用matlab軟件對帶交易費用的信息控制投資組合模型進行求解,所得結果如表7和圖3所示。結果表明:隨著交易費用比例的增大,目標函數值在逐漸變小,資產配置的分散程度逐漸變小,由于交易費用的增大,資產收益降低,從而導致投資組合的風險值降低,且基于信息控制的投資組合模型比一般的投資組合模型具有更低的風險。

表7 不同的交易費用比例下CIP模型的計算結果
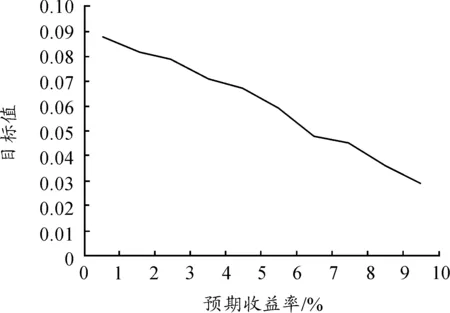
圖3 不同的交易費用比例下CIP模型的計算結果
5 結束語
本文通過將信息風險函數引入投資組合模型,構建更加符合實際的帶交易費用的信息控制模型,與傳統的帶交易費用的投資組合模型進行了比較,并且通過數學規劃中的罰函數算法對模型進行求解。進行了模型的實證分析,驗證了該模型和罰函數算法的有效性。實證分析結果表明:同傳統的帶交易費用的模型相比,帶交易費用的信息控制模型具有較低的投資組合風險,且隨著投資者預期收益率的不斷提高,模型的目標值也逐漸增大,即投資組合的風險在逐步增加。
[1] HARRY M.Portfolio selection[J].Journal of Finance,1952,7(1):113-124.
[2] SHARPE W F.A Simplified Model for Portfolio Analysis[J].Management Science,1963,(3):13-26.
[3] EASTHAM J E,HASTING K J.Optimal impulse control of portfolios[J].Mathematical Programming,2008(4):11-24.
[4] 趙春峰.基于條件風險價值(CVaR)投資組合模型的分析及應用[D].成都:西南財經大學,2010.
[5] 梁素紅.組合投資數學模型發展的研究[D].長春:吉林大學,2011.
[6] 王貞.幾類投資組合優化模型及其算法[D].西安:西安電子科技大學,2012.
[7] 申飛飛,楊柳.基于CVaR的債券投資組合模型[J].經濟數學,2014(2):56-59.
[8] 楊梅.凸規劃和模糊線性規劃模型在組合投資中的應用[J].統計與決策,2013(10):59-63.
[9] 張波,陳睿君,路璐.粒子群算法在投資組合中的應用[J].系統工程,2007,25(8):108-110.
[10]文鳳華,馬超群,陳牡妙,等.一致性風險價值及其算法與實證研究[J].系統工程理論與實踐.2004,24(10):15-21.
[11]BOUDOUKH J,WHITELAW R.The benchmark effect in the Japanese government bood market[J].Applied Mathematics and Computation,2009,(2):23-38.
[12]KONNO H,YAMAKAZI H.Mean-absolute deviation portfolio optimization model and its applications to Tokyo stock market[J].SIAM Journal on Optimization,2007(4):112-131.
(責任編輯 陳 艷)
Model of Portfolio Optimization Based on Information Control and Transaction Cost
LI A-na, SUN Hua-dong, JING Yong-qiang
(School of Science, North University of China, Taiyuan 030051, China)
This paper constructed a more realistic portfolio information control model with transaction costs and the information risk function, and the information control portfolio model with transaction costs was compared to the traditional portfolio model with transaction costs. The model was solved by the penalty function algorithm in mathematical programming. The validity of the model and penalty function algorithm was verified through the empirical analysis of the model.
transaction cost; mathematical model; penalty function; information control; portfolio
2016-01-12
電子測試技術國家重點實驗室基金資助項目(9140C120401080C12);中北大學科學基金資助項目(201406)
李阿娜(1989—),女,山西運城人,碩士研究生,主要從事最優化模型及其數值方法研究,E-mail:454252140@qq.com; 孫華東(1965—),男,教授,碩士生導師,主要從事彈塑性動力學、計算力學研究。
李阿娜,孫華東,景永強.基于交易費用的信息控制投資組合模型[J].重慶理工大學學報(自然科學),2017(4):163-168.
format:LI A-na, SUN Hua-dong, JING Yong-qiang.Model of Portfolio Optimization Based on Information Control and Transaction Cost[J].Journal of Chongqing University of Technology(Natural Science),2017(4):163-168.
10.3969/j.issn.1674-8425(z).2017.04.027
F830.59
A
1674-8425(2017)04-0163-06

