軟式非線性同步振動(dòng)沉樁系統(tǒng)的動(dòng)力學(xué)分析*
張 楠, 邱燕超, 張學(xué)良, 聞邦椿
(1.北京建筑大學(xué)城市軌道交通車輛服役性能保障北京市重點(diǎn)實(shí)驗(yàn)室 北京,102616) (2.東北大學(xué)機(jī)械工程與自動(dòng)化學(xué)院 沈陽(yáng),110819)
?
軟式非線性同步振動(dòng)沉樁系統(tǒng)的動(dòng)力學(xué)分析*
張 楠1, 邱燕超1, 張學(xué)良2, 聞邦椿2
(1.北京建筑大學(xué)城市軌道交通車輛服役性能保障北京市重點(diǎn)實(shí)驗(yàn)室 北京,102616) (2.東北大學(xué)機(jī)械工程與自動(dòng)化學(xué)院 沈陽(yáng),110819)
對(duì)軟式非線性同步振動(dòng)沉樁系統(tǒng)進(jìn)行動(dòng)力學(xué)特性研究。首先,建立同步振動(dòng)沉樁系統(tǒng)的軟式非線性振動(dòng)模型,采用一次近似解的幅頻特性方程判定系統(tǒng)周期解穩(wěn)定性問題;然后,利用選取的參數(shù)分析系統(tǒng)幅頻特性關(guān)系,并且根據(jù)幅頻特性曲線確定系統(tǒng)多解處的穩(wěn)定解問題,以及討論沉樁系統(tǒng)參數(shù)(激振頻率、土的剛度和阻尼、激振器的偏心距等)對(duì)系統(tǒng)動(dòng)力學(xué)特性的影響;最后,基于Matlab/Simulink采用四階龍格-庫(kù)塔法運(yùn)算程序進(jìn)行數(shù)值仿真確定系統(tǒng)周期解穩(wěn)定性。通過理論和仿真系統(tǒng)地分析了系統(tǒng)周期解的穩(wěn)定性特性,以及系統(tǒng)各參數(shù)對(duì)系統(tǒng)周期解的影響。
非線性振動(dòng); 幅頻特性; 穩(wěn)定性; 同步振動(dòng)沉樁系統(tǒng)
引 言
同步振動(dòng)沉樁系統(tǒng)是通過兩激振電機(jī)回轉(zhuǎn),進(jìn)行振動(dòng)沉樁的。在振動(dòng)沉樁系統(tǒng)沉樁過程中,激振電機(jī)上的偏心轉(zhuǎn)子反向回轉(zhuǎn),只產(chǎn)生豎直方向的激振力來達(dá)到沉樁的目的。由雙激振電機(jī)偏心轉(zhuǎn)子反向回轉(zhuǎn)所組成的振動(dòng)沉樁系統(tǒng)稱為自同步振動(dòng)沉樁系統(tǒng)。當(dāng)非線性自同步振動(dòng)沉樁系統(tǒng)的激振電機(jī)的激振頻率與系統(tǒng)的一階固有頻率接近一致時(shí),其激振電機(jī)的激振頻率被系統(tǒng)的一階固有頻率所俘獲,此時(shí)稱為系統(tǒng)發(fā)生頻率俘獲現(xiàn)象[1-2]。系統(tǒng)在頻率俘獲情況下,系統(tǒng)的沉樁振幅最大、沉樁速度快、沉樁效率高。
自同步振動(dòng)系統(tǒng)中存在各種形式的非線性因素,而自同步振動(dòng)系統(tǒng)中非線性因素將對(duì)系統(tǒng)的動(dòng)力學(xué)行為產(chǎn)生重要的影響[3-5]。關(guān)于自同步振動(dòng)系統(tǒng),國(guó)內(nèi)外許多學(xué)者從線性或擬線性化角度把系統(tǒng)簡(jiǎn)化為理想系統(tǒng)進(jìn)行動(dòng)力學(xué)特性分析[6-9],有少數(shù)學(xué)者也考慮到系統(tǒng)模型的非線性特性[10]。另外許多同步振動(dòng)系統(tǒng)是在遠(yuǎn)超共振狀態(tài)下進(jìn)行相關(guān)研究[11-15],這些研究并沒系統(tǒng)研究系統(tǒng)周期解的穩(wěn)定性。系統(tǒng)解的穩(wěn)定性是同步振動(dòng)系統(tǒng)重要的特性,因此,需深入研究同步振動(dòng)系統(tǒng)的非線性動(dòng)力學(xué)行為及其周期解穩(wěn)定性。
1 建立模型
在同步振動(dòng)沉樁系統(tǒng)工作過程中,樁土相互作用非常復(fù)雜,根據(jù)土壤應(yīng)力-應(yīng)變關(guān)系,把樁土之間相互作用采用軟式非線性彈性力來表示土壤的非線性特性,軟式非線性彈性力可表示為k(y)=ky-εk′y3,式中k為土壤線性彈性剛度,y為樁的位移,ky為線性彈性力,ε為非線性系數(shù)(為小的整數(shù)),εk′y3為非線性彈性力,通常要比ky小。當(dāng)同步振動(dòng)沉樁系統(tǒng)的激振力由電動(dòng)機(jī)驅(qū)動(dòng)時(shí),雙激振電機(jī)反向回轉(zhuǎn),振動(dòng)沉樁系統(tǒng)在豎直方向工作,其振動(dòng)沉樁系統(tǒng)非線性動(dòng)力學(xué)模型如圖1所示。圖中,Oxy為非線性振動(dòng)系統(tǒng)坐標(biāo)系,O為振動(dòng)沉樁中心(同時(shí)為兩激振電機(jī)回轉(zhuǎn)軸心連線的中點(diǎn)),O1,O2為兩激振器回轉(zhuǎn)軸心。
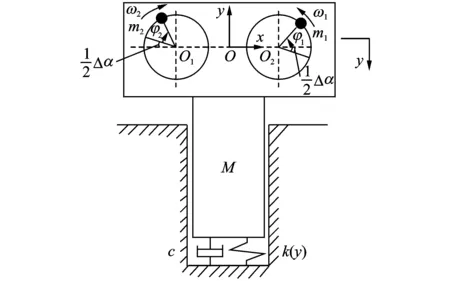
圖1 非線性動(dòng)力學(xué)模型Fig.1 Nonlinear dynamic model
采用拉格朗日方程得到樁-土耦合動(dòng)力學(xué)模型如下
(1)
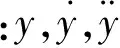
2 模型解析
其中所有的ε系數(shù)相等,得
(5)
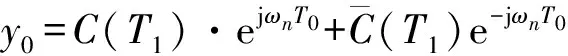
將通解代入式(5)第二個(gè)式子中得到
(6)
需要去掉長(zhǎng)期項(xiàng)的條件是
(7)
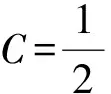
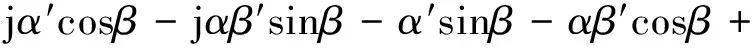
(8)
式(8)中所有實(shí)部和虛部相等,可以得
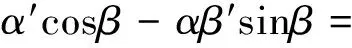
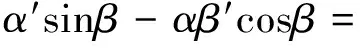
(9)
式(9)中第1個(gè)式子乘以sinβ與第2個(gè)式子乘以cosβ然后相加,或者式(9)中第1個(gè)式子乘以cosβ與第2個(gè)式子乘以sinβ然后相減,最終整理得到下面兩個(gè)式子,即
(10)
將式(10)變換為一個(gè)自治系統(tǒng)(即不顯含T1的系統(tǒng)),設(shè),γ′=σ-β′,β′=σ-γ′,則式(10)變?yōu)?/p>
(11)
由于系統(tǒng)在穩(wěn)定狀態(tài)時(shí),其α′=β′=0,因此式(11)變?yōu)?/p>
(12)
式(12)中的兩個(gè)式子平方后相加得
(13)
式(13)整理得
(14)
因此,振動(dòng)沉樁系統(tǒng)頻率俘獲情況下的一次近似解為
(15)

(16)
其中參數(shù)由式(14)確定。
3 系統(tǒng)解的穩(wěn)定性
如果確定式(13)中的α和γ,就可以確定原系統(tǒng)的一個(gè)周期解即式(16)。因此分析α和γ的穩(wěn)定性問題,就能確定系統(tǒng)解的穩(wěn)定性問題。于是,可以把式(11)進(jìn)行變換求解,設(shè)

(17)
式(11)整理得到
(18)
式(18)第1式乘以cosγ與第2式乘以sinγ相減得
(19)
同理,式(18)第1式乘以sinγ與第2式乘以cosγ相加得
(20)
式(19)和(20)整理得到新的方程為
(21)
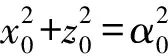
4 幅頻特性分析
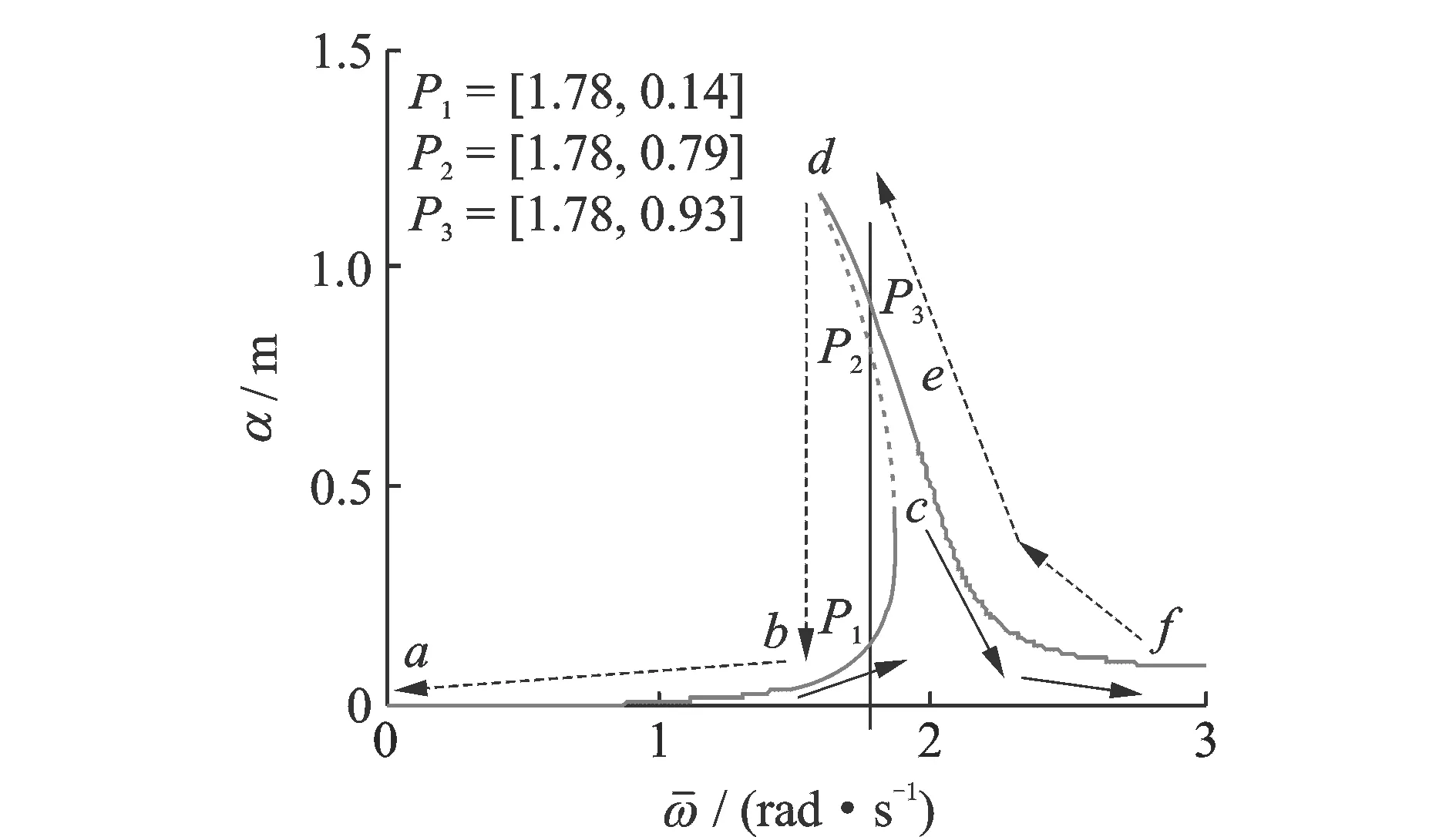
圖2 幅頻特性Fig.2 Amplitude-frequency characteristic
系統(tǒng)參數(shù)變化導(dǎo)致幅頻特性變化如圖3所示。由圖顯示,整個(gè)系統(tǒng)的其他參數(shù)不變,僅改變土壤的非線性系數(shù)ε,隨著ε變小,振幅顯著增加,且軟式非線性系統(tǒng)就越接近線性振動(dòng)系統(tǒng),如果系統(tǒng)不考慮非線性因素時(shí),即ε=0,則曲線變?yōu)榫€性系統(tǒng)幅頻特性曲線。當(dāng)增大土壤線性彈性系數(shù)k,幅頻特性曲線向右移動(dòng),由于激振頻率產(chǎn)生激振力,激振頻率不斷變化,激振力也是變化的,因此幅頻特性曲線彎曲程度有些變大。當(dāng)減小土壤阻尼系數(shù)c或者增加激振力上的偏心距(偏向轉(zhuǎn)子的半徑r0與質(zhì)量m0的乘積),比如增加偏心塊半徑時(shí),同步振動(dòng)沉樁系統(tǒng)的振幅峰值增大,曲線彎曲程度變大。
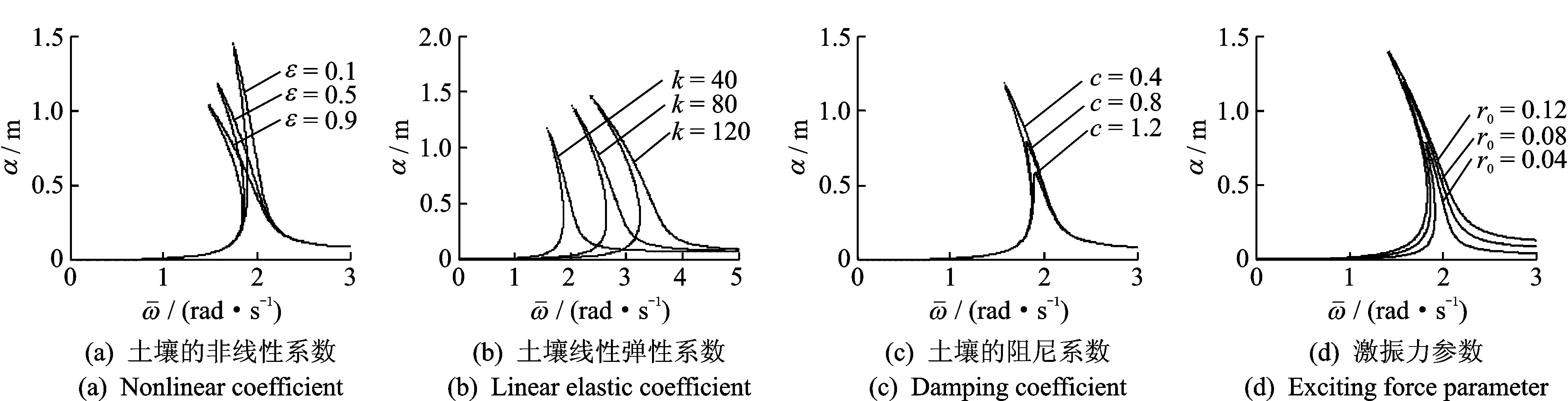
圖3 參數(shù)變化對(duì)振幅的影響Fig.3 Influence of parameter variation on amplitude
5 系統(tǒng)解的穩(wěn)定性計(jì)算與仿真
式(21)的雅可比矩陣的特征方程為
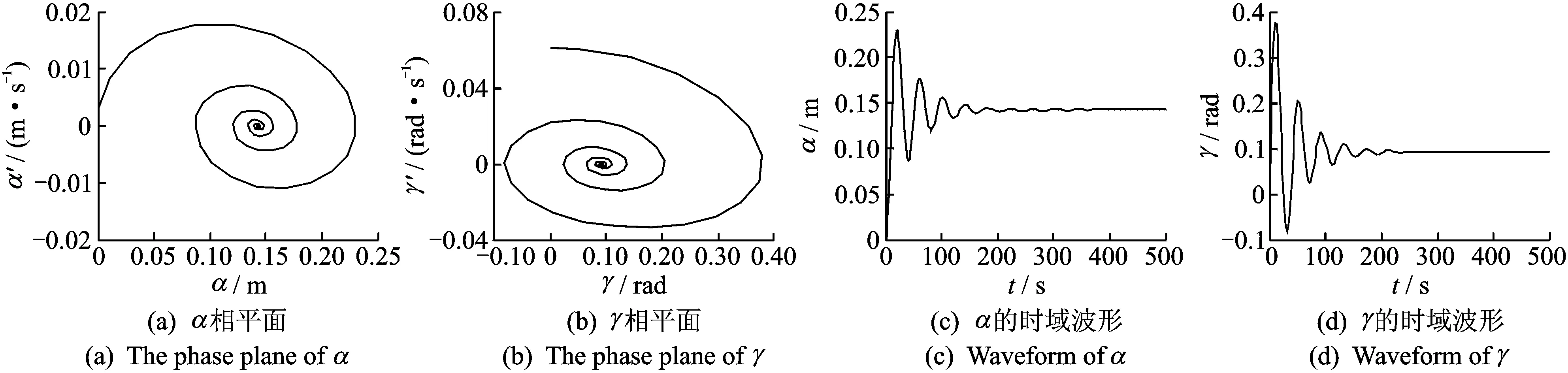
圖4 αt=0=0 m,γt=0=0 rad時(shí)相平面圖和軌跡圖Fig.4 Phase plane and waveform in αt=0=0 m and γt=0=0 rad
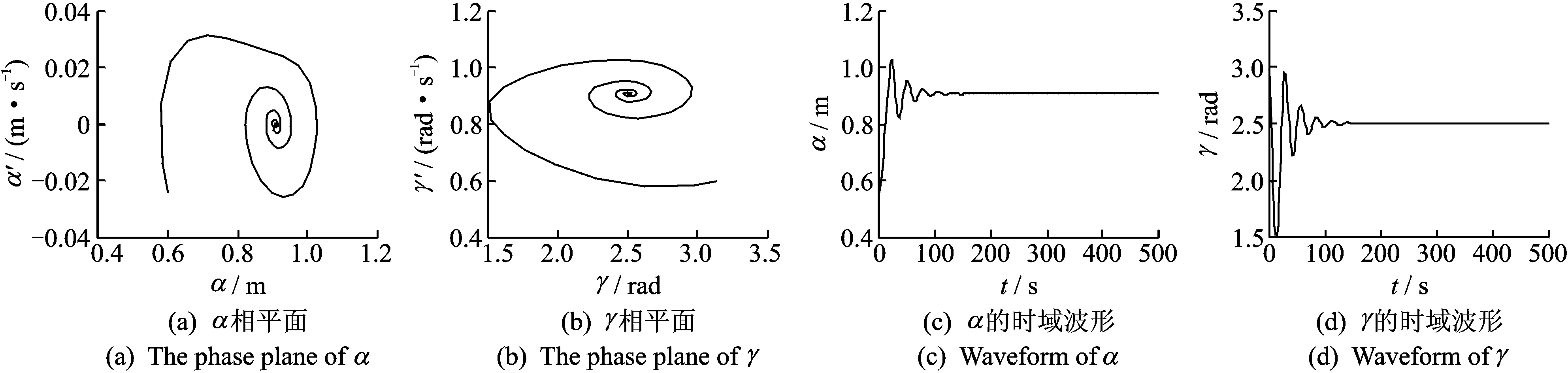
圖5 αt=0=0.6 m,γt=0=3.14 rad時(shí)相平面圖和軌跡圖Fig.5 Phase plane and waveform in αt=0=0.6 m,γt=0=3.14 rad
6 結(jié) 論
1) 理論推導(dǎo)系統(tǒng)在頻率俘獲情況下一次近似解,以及理論上討論周期解的穩(wěn)定性判據(jù)問題,也利用幅頻特性方程和穩(wěn)定解相平面圖來實(shí)際分析系統(tǒng)解的穩(wěn)定性問題,且理論和計(jì)算仿真分析相一致。
2) 同步振動(dòng)沉樁系統(tǒng)的激振頻率在一定范圍時(shí),系統(tǒng)將出現(xiàn)多個(gè)定常解,兩個(gè)是穩(wěn)定的,而另一個(gè)是不穩(wěn)定的。系統(tǒng)最終穩(wěn)定在那個(gè)穩(wěn)定點(diǎn)取決于系統(tǒng)的初始條件,而出現(xiàn)跳躍現(xiàn)象的地方,都是自發(fā)跳躍到穩(wěn)定點(diǎn)位置而與初始條件無(wú)關(guān)。選擇合適的初始位移,以便獲得大的沉樁振幅。
3) 在保證系統(tǒng)發(fā)生頻率俘獲的前提下,適當(dāng)改變系統(tǒng)參數(shù),可以提高系統(tǒng)的最大振幅的平穩(wěn)性。表明土壤阻尼小、土壤的剛度大或者增加激振力,可增大振幅并提高系統(tǒng)的沉樁速度。
[1] Blekhman I I. The Setting up of the self-synchronization problem of the dynamic objects with internal degrees of freedom and methods of its solution[J]. Journal of Biological Chemistry, 2014, 260(24):13321-13327.
[2] Zhao Chunyu, Zhao Qinghua, Zhang Yimin, et al. Synchronization of two non-identical coupled exciters in a non-resonant vibrating system of plane motion[J]. Journal of Mechanical Science & Technology, 2011, 25(1):49-60.
[3] Panovko G Y, Shokhin A E, Eremeikin S A. Experimental analysis of the oscillations of a mechanical system with self-synchronized inertial vibration exciters[J]. Journal of Machinery Manufacture & Reliability, 2015, 44(6):492-496.
[4] Pound B, Macala J, Mokhothu N. Theoretical and experimental study on synchronization of the two homodromy exciters in a non-resonant vibrating system[J]. Shock & Vibration, 2013, 20(2):327-340.
[5] 來鑫, 烏建中, 阮博. 樁錘同步振動(dòng)系統(tǒng)的機(jī)電耦合數(shù)值仿真分析與試驗(yàn)[J].振動(dòng)工程學(xué)報(bào),2012, 25(2): 167-173.
Lai Xin, Wu Jianzhong, Yuan Bo. Numerical simulation and experiments on electromechanical coupling characteristics of pile hammer synchronous vibration system[J].Journal of Vibration Engineering, 2012, 25(2): 167-173.(in Chinese)
[6] Zhang Xueliang, Wen Bangchun, Zhao Chunyu. Experimental investigation on synchronization of three co-rotating non-identical coupled exciters driven by three motors[J]. Journal of Sound and Vibration, 2014, 333(13): 2898-2908.
[7] 李鶴,劉丹, 趙春雨,等. 雙機(jī)驅(qū)動(dòng)無(wú)擺動(dòng)振動(dòng)機(jī)的自同步理論研究[J]. 振動(dòng)、測(cè)試與診斷, 2015, 35(3):541-546.
Li He, Liu Dan, Zhao Chunyu, et al. Self-synchronous theory of no-swing vibrating machine driven by dual-motor[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(3):541-546. (in Chinese)
[8] Zhao Chunyu, Wen Bangchun, Zhang Xueliang. Synchronization of the four identical unbalanced rotors in a vibrating system of plane motion[J]. Science China Technological Sciences, 2010, 53(2):405-422.
[9] 李葉, 李鶴, 耿志遠(yuǎn), 等. 手持式振動(dòng)機(jī)械的同步問題[J]. 振動(dòng)、測(cè)試與診斷, 2013, 33(S1):9-14.
Li Ye, Li He, Geng Zhiyuan, et al. Self-synchronization of hand-held vibrating machinery[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(S1): 9-14. (in Chinese)
[10]李小號(hào), 陳述平, 劉杰. 非線性振動(dòng)系統(tǒng)基于頻率俘獲現(xiàn)象的諧振同步分析[J]. 機(jī)械工程學(xué)報(bào),2014,50(3):100-107.
Li Xiaohao, Chen Shuping, Liu Jie. Harmonic vibration synchronization analysis of nonlinear vibration system based on frequency catching phenomenon[J]. Journal of Mechanical Engineering. 2014, 50(3): 100-107. (in Chinese)
[11]Fang Pan, Yang Qiming, Hou Yongjun, et al. Theoretical study on self-synchronization of two homodromy rotors coupled with a pendulum rod in a far-resonant vibrating system[J]. Journal of Vibroengineering, 2014, 16(5):2188-2204.
[12]Zhang Xueliang, Wen Bangchun, Zhao Chunyu. Vibratory synchronization and coupling dynamic characteristics of multiple unbalanced rotors on a mass-spring rigid base[J]. International Journal of Non-Linear Mechanics, 2013, 60(2):1-8.
[13]Alqahtani A, Khenous H B, Aly S. Self-synchronization in a system of nonlinear van der pol oscillators[J]. Applied Mathematics, 2015, 6(6): 922-932.
[14]Potapenko M A. Influence of an additional degree of freedom of the oscillating part of a system on the self-synchronization of mechanical vibration exciter[J]. Journal of Machinery Manufacture & Reliability, 2015, 44(6):497-501.
[15]Zhang Xueliang, Zhao Chunyu, Wen Bangchun. Synchronization of three non-identical coupled exciters with the same rotating directions in a far-resonant vibrating system[J]. Journal of Sound and Vibration, 2013, 332(9): 2300-2317.

*國(guó)家自然科學(xué)基金資助項(xiàng)目(51605022);北京建筑大學(xué)科學(xué)研究基金資助項(xiàng)目(00331616043)
2015-12-01;
2016-04-08
10.16450/j.cnki.issn.1004-6801.2017.02.018
TH113.1; O322
張楠,女,1979年10月生,博士、講師。主要研究方向?yàn)闄C(jī)械動(dòng)力學(xué)、振動(dòng)同步。曾發(fā)表《脈動(dòng)流誘發(fā)振動(dòng)轉(zhuǎn)子密封系統(tǒng)特性分析》(《清華大學(xué)學(xué)報(bào)》2014年第54卷第7期)等論文。 E-mail: zhangnan@bucea.edu.cn

