考慮大變形的大展弦比機翼氣動彈性優化設計

王斐， 李秋彥， 謝長川， 孟楊

(1.成都飛機設計研究所， 成都610091；2.北京航空航天大學航空科學與工程學院， 北京100191)

考慮大變形的大展弦比機翼氣動彈性優化設計

王斐1， 李秋彥1， 謝長川2， 孟楊2

(1.成都飛機設計研究所， 成都610091；2.北京航空航天大學航空科學與工程學院， 北京100191)

針對大展弦比機翼飛機自身特點，在結構大變形情況下，將彈性力學幾何非線性理論引入到大柔性飛行器的氣動彈性力學分析中，建立完整的幾何非線性氣動彈性分析方法框架。該方法主要包含兩方面：結構非線性剛度和曲面氣動力的計算。結合優化設計，為了提高優化設計效率，針對迭代過程進行有效簡化。基于ISIGHT優化平臺，發展一種適用于初步設計階段大展弦比機翼在大變形情況下的氣動彈性優化設計方法，有效地避免了結構大變形情況下線性氣動彈性分析造成的設計偏差。為了擺脫對初始設計點的依賴，結合局部算法，采用組合優化策略，開展了大展弦比機翼的幾何非線性氣動彈性優化設計，首先應用蟻群算法定位目標極值在設計空間中所處的區域，再應用直接搜索算法對該區域精確尋優，獲得更加準確的設計結果。

氣動彈性;大展弦比;幾何非線性;氣動彈性優化設計;直接搜索法;蟻群算法

引言

現代飛機由于不斷追求減輕結構重量和提高飛行性能，使得氣動彈性問題變得愈加突出。大柔性飛行器的氣動彈性研究是近年高空長航時無人機和大型運輸機的設計需求。該類飛機在飛行過程中具有大變形的特征，尤其在陣風和機動過程中，靜/動力學變形問題更為突出，通常在線性小變形假設情況下進行研究的氣動載荷分布、動力學響應、靜彈性和顫振等問題的邊界條件受到較大改變，因此結構大變形對氣動彈性的影響必須予以考慮。國內外的初步研究均表明，一方面，結構大變形造成機翼有效升力的變化，從而進一步改變了結構設計的載荷條件；另一方面，結構幾何非線性因素在一定的結構變形程度下會顯著降低飛行器的氣動彈性穩定性(可以達到10%以上)，這就有可能降低飛行器顫振余量，影響其飛行安全。因此，大變形對這類飛機帶來的影響，給傳統飛機設計理念和方法帶來了挑戰。這是由于進行幾何非線性氣動彈性分析時，結構相應變形沒有轉化成約束條件參與分析，所以使得設計偏離真實算例，造成設計上的偏差[1]。

針對大展弦比機翼飛機自身特點，利用氣動彈性優化設計技術，考慮大變形時結構幾何非線性的影響，將幾何非線性氣動彈性分析與氣動彈性優化技術結合起來，建立一種適用于考慮大變形的幾何非線性氣動彈性優化設計方法。在上述基礎上繼續探索優化效率的提高，完善初步設計階段的氣動彈性優化方法體系，使得飛機初步階段設計更具有合理性和高效性。

1理論基礎

在外載荷作用下，大展弦比柔性機翼會發生顯著的彎曲變形和扭轉變形，傳統基于小變形假設的線性求解方法不再適用，但結構應變并不大，本構關系仍為線性，即形成幾何非線性問題。從結構力學和空氣動力學兩方面都考慮了幾何非線性因素的氣動彈性問題可稱為幾何非線性氣動彈性[2]。主要涉及三方面的基礎理論，分別為結構幾何非線性理論，結構變形后曲面氣動力分析方法以及相應的結構/氣動界面耦合方法。

考慮到結構模型的工程適用性，機翼結構采用較為通用的非線性有限元模型[2-3]，大變形機翼的氣動力計算采用考慮曲面效應的偶極子格網法[4-5]。隨著結構變形的增大，氣動力方向也隨著改變，因此還需要考慮定常氣動力的隨動加載。氣動網格劃分示意如圖1所示，總體氣動坐標系定義X軸正向沿來流方向，Y軸正向為沿翼展向外，Z軸正向由右手定則確定。對于考慮大變形情況需要定義局部氣動坐標系，其原點位于網格分塊1/4弦線的中點處，x軸指向來流方向，s軸正方向沿1/4弦線向右，n軸為曲面網格的局部法向。

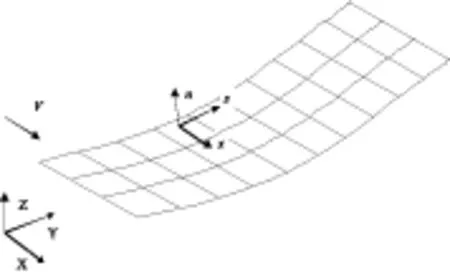
圖1曲面氣動面網格示意圖

結構/氣動界面的位移和力傳遞通過曲面樣條插值函數實現[6]，該方法是基于彈性薄板解析解的無限平板樣條(IPS)及其三維推廣的薄板樣條(TPS)方法，廣泛應用于氣動彈性界面耦合求解之中，并成為商用軟件如NASTRAN與ZAERO的標準插值方法。其主要思路為：已知某一坐標平面上n個任意分布的獨立節點及其對應的位移，以此確定曲面樣條函數的待定系數，樣條函數確定后，位移的插值形式為：

UA=GUS

(1)

其中，G為由結構到氣動結點的位移插值矩陣。由虛功等效可以得到載荷的插值形式：

FS=GTFA

(2)

2分析流程

大展弦比柔性機翼氣動彈性分析是靜、動力學相互耦合的。幾何非線性靜氣動彈性分析包括非線性結構靜力分析、大變形定常氣動力計算和結構/氣動界面的耦合迭代。在變形后的結構上計算定常氣動力，并插值到結構上，采用非線性結構求解器計算新的變形，如此迭代直到達到一定的精度要求，認為結構滿足平衡條件，從而得到非線性靜平衡態，如圖2所示，此時可以給出結構變形和定常氣動力特性。

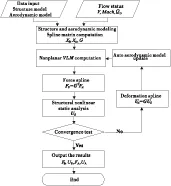
圖2幾何非線性靜氣動彈性分析流程圖

基于非線性靜氣動彈性平衡狀態，得到系統動力學線化方程的各系數矩陣，采用“準模態法”[2]進行幾何非線性顫振分析，即假設結構在較大靜變形平衡位置附近作微幅振動，繼續沿用線性系統振動理論中的固有頻率和模態的概念，顫振分析方法采用p-k法[7]。然而這樣僅能計算出該平衡態的預測顫振速度，無法得到確切的顫振臨界速度，這是因為來流速度不同，系統的平衡態會發生變化，所以需要迭代求解，直到預測顫振速度收斂到來流速度為止，如圖3所示。

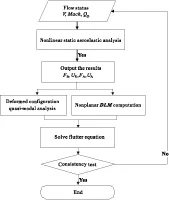
圖3幾何非線性顫振分析流程圖

3算例仿真

3.1模型基本參數

機翼動力有限元模型如圖4所示，主梁提供機翼整體剛度，離散質量點模擬質量特性。弦向的梁單元主要用于表現扭轉變形并進行氣動力插值。模型基本參數見表1。

圖4有限元模型

表1機翼模型參數

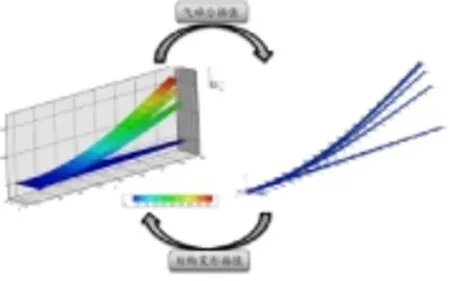
圖5展示了風速為37m/s算例下的計算過程，左邊表示氣動面的迭代變形過程，右邊為結構的迭代變形過程。從圖5可以明顯看到相對變形越來越小，最后收斂。

圖5迭代過程示意圖

3.2優化策略

結合優化設計，為了提高優化設計效率，針對迭代過程進行有效簡化。非線性靜氣動彈性分析計算效率低，主要是因為需要迭代。但是在靜氣動彈性優化分析時，如果設計參數變化不大，那么同等算例下，收斂狀態的變形位置和氣動力分布也不會發生太大變化，對于這種情況可以考慮直接引入前一次尋優的平衡態載荷，而不進行迭代分析，采用近似的方法獲得非線性靜氣動彈性響應結果。通過這種方法可以有效地減小工作量，提高分析效率。具體計算步驟為：

(1) 將前一次尋優迭代后的穩態載荷，作用到新的結構上，獲得靜變形Ui。

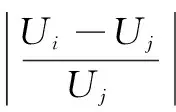
(3) 若滿足，直接采用前一次尋優的穩態載荷，得到靜氣動彈性響應，然后進行顫振分析。

(4) 若不滿足，進行靜氣動彈性迭代分析，獲得靜平衡態載荷和變形，然后進行顫振分析。

(5) 無需得到具體的顫振速度，只判定顫振速度是否滿足邊界條件。

為了研究相對變形對非線性氣動彈性分析結果的影響，對判定參考值ε取不同值進行優化分析，并與不采用簡化方法對比，即ε=0%。計算時間結果如圖6所示，采用簡化方法優化后計算時間明顯減少，其中參考值取為1%時計算時間最長，主要是因為其判定條件最嚴格，大部分優化過程仍然采用迭代計算。結果顯示判定參考值取為3%時，計算時間最短，當判定參考值取得更大時，由于分析結果的不準確，對優化算法的尋優過程會產生較大影響，計算時間反而增加。以不采用簡化方法的優化結果為標準，計算各判定參考值的相對誤差，如圖7～圖10所示。結構總重、顫振速度以及最大位移誤差都在3%以內，但是判定參考值取為5%和9%時根部應力結果偏差較大。總的來說判定參考值為3%時，優化結果最準確。綜合考慮計算效率和優化結果的準確性，本文中靜氣動彈性迭代過程的判定參考值取為3%。

圖6計算時間對比

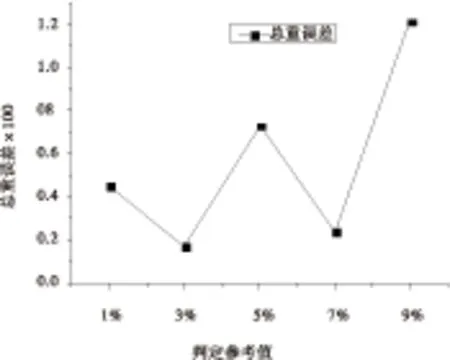
圖7總重相對誤差

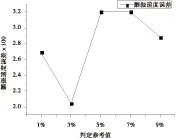
圖8顫振速度相對誤差

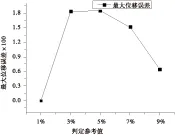
圖9最大位移相對誤差

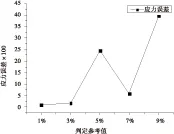
圖10應力相對誤差

3.3算例1優化結果

3.3.1約束條件

以機翼2g機動飛行狀態為設計背景，針對主梁的截面尺寸進行優化設計，以主梁的重量最小為優化目標，要求變形在10%以內，剛度和強度在安全范圍內，在一定的速度下不發生顫振，約束條件為：

(1) 海平面高度，飛行速度20m/s，2g過載配平狀態，翼尖位移約束utop≤154(10%)mm。

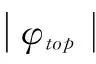
(3) 海平面高度，機翼顫振速度VF≥50m/s。

(4) 主梁各段靠近翼根處端面，最大應力約束為σmax≤350MPa，安全系數取為1.5。

3.3.2線性優化

大展弦比機翼線性優化不考慮由于機翼大變形帶來的剛度非線性和氣動力曲面效應的影響。優化算法采用局部優化算法HJ法。設定一組合適的主梁截面尺寸初始值，最大優化迭代1000次，相對步長取為0.05，減縮因子取為0.5。迭代過程如圖11所示，迭代過程反應了HJ法的兩類移動方式，局部變動表示的是算法探測性移動，相對幅度較大的跳躍是算法沿一個有前途方向加速移動的模式性移動。

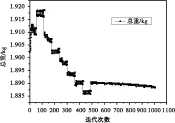
圖11線性優化迭代過程

線性優化結果見表2，顫振速度剛好達到約束條件下限，而位移約束還有一定的空間，總重降低0.7%。顫振耦合形式沒有發生改變，穿越模態都是一階扭轉。

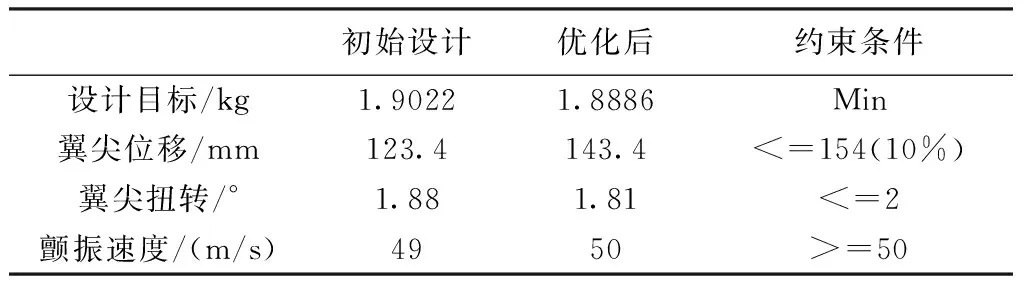
表2線性優化結果對比

3.3.3幾何非線性分析

將線性優化結果進行幾何非線性分析，結果見表 3。考慮機翼受載變形后，結果發生了明顯變化，其中翼尖位移和顫振速度都沒有滿足約束條件。這表明當機翼發生較大變形時，傳統的基于小變形假設的氣動彈性優化不再適用，得到的最優解在真實工況下時有可能不滿足約束條件，所以發展適用于大變形的氣動彈性優化方法是十分必要的。

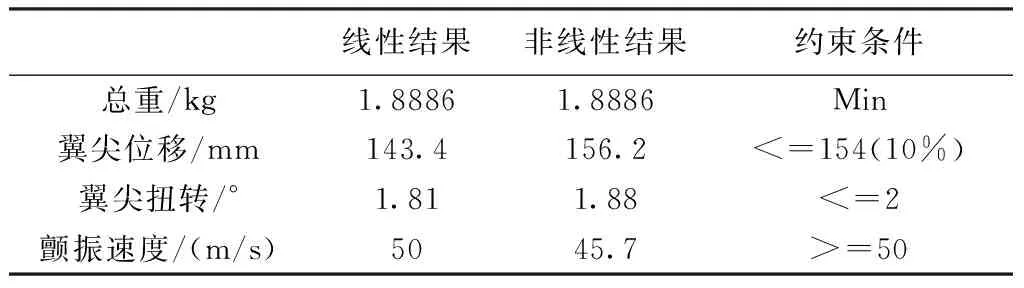
表3線性與非線性分析結果對比

線性和非線性模態結果見表 4，當風速達到45.7m/s時，翼尖變形已經達到17%，不僅使前四階非線性模態頻率(考慮結構變形后的模態頻率)降低，顫振速度降低，而且顫振耦合形式也發生了改變，水平模態參與了顫振。

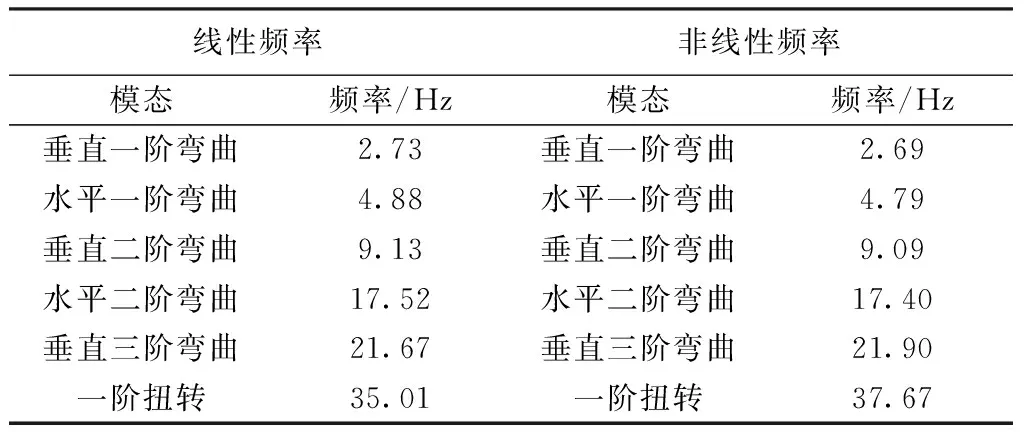
表4線性與非線性模態對比

3.3.4幾何非線性優化

約束條件不變，初始值采用線性優化結果，設計目標、設計變量和優化算法參數與線性優化相同。通過幾何非線性優化，最終得到滿足真實約束條件的設計結果，見表5，顫振速度提高9%，重量上付出了1.5%的代價。

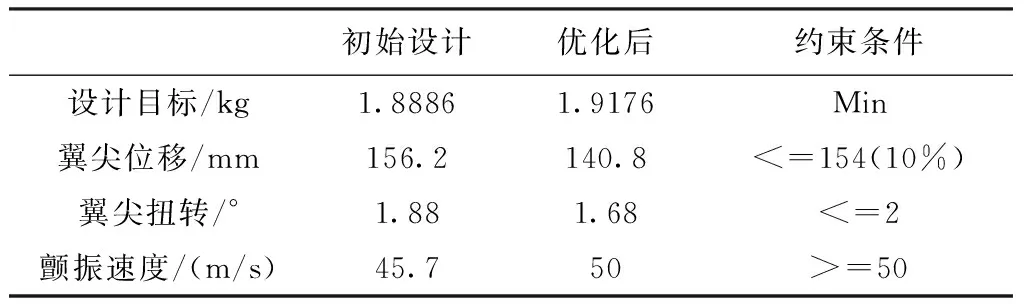
表5算例1優化結果對比

3.4算例2優化結果

3.4.1約束條件

以大變形低速風洞模型設計為背景，同樣針對主梁的截面尺寸進行優化設計，以主梁的重量最小為優化目標，要求變形達到25%以上，顫振速度在一定的范圍內，約束條件變為：

(1) 機翼顫振速度(m/s)約束36≤Vf≤40。

(2) 顫振速度下，翼尖位移(mm)約束為：380(25%)≤utop≤550(36%)

(4) 主梁各段靠近翼根處端面，最大應力約束為σmax≤350MPa，安全系數取為1.5。

3.4.2局部算法幾何非線性優化

重新給定一組合適的主梁截面尺寸初始值，計算來流速度設置為顫振速度約束下邊界36m/s，優化算法參數不變，直接開展幾何非線性氣動彈性優化設計。迭代過程如圖12所示，目標函數經過531次計算，獲得收斂。

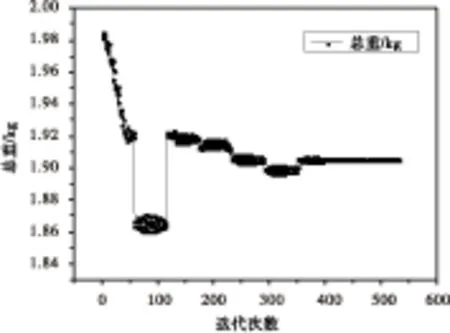
圖12算例2優化迭代過程

優化結果見表6，優化前機翼模型的翼尖扭轉角和非線性顫振速度都偏大，對風洞流場穩定性和模型安全性都是不利的，通過優化后，顫振速度降低到設計要求范圍內，同時滿足約束條件，總重達到最小，顫振速度下降12%，總重下降了4%，表明初始設計狀態是過剛度。優化前后頻率對比見表 7，主要的顫振耦合模態垂直一階彎曲頻率下降23.6%，水平一階彎曲頻率下降22.6%，一階扭轉下降9.6%，進而使得顫振速度降低。

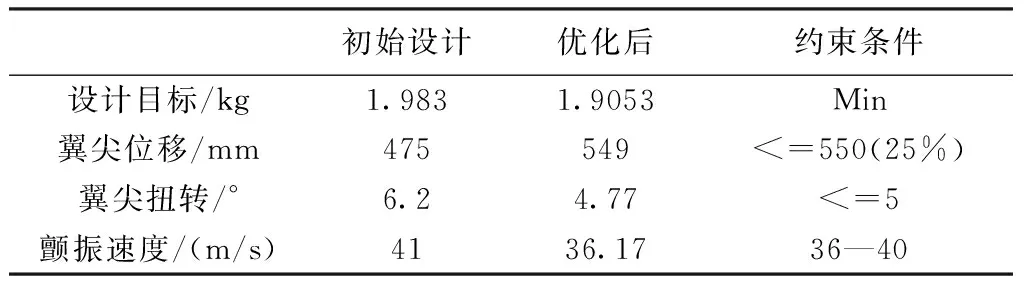
表6算例2優化結果對比

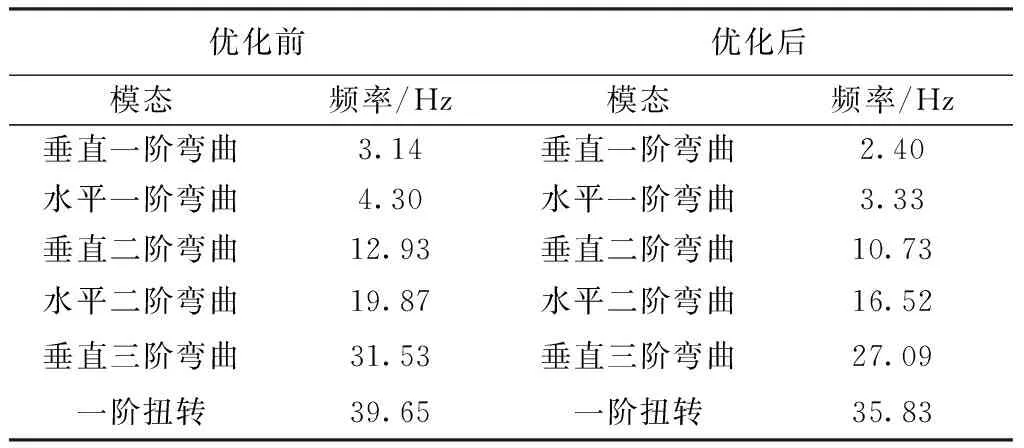
表7算例2模態頻率對比

3.4.3組合優化

為了擺脫對初始設計點的依賴，本文采用組合優化策略，通過集成蟻群算法和直接搜索算法[11-13]進行優化設計。首先發揮蟻群算法的優勢，進行有效的全局尋優，在整個設計空間中定位目標極值，然后發揮直接搜索算法精度高而且速度快的優勢，對該區域精確尋優。

直接搜索法、蟻群算法和組合優化三種方法的優化結果對比見表 8。從表8可知，采用組合優化策略的方式，在滿足氣動彈性性能指標的同時，結構總重最小，獲得相對更加優秀的設計方案。單獨采用直接搜索法得到的最優結果總重最大，可見初值的選取對局部算法的結果影響很大。但是在實際工程設計中，依靠工程經驗給出的初始設計方案，相對而言比較可靠，因此局部算法憑借優化效率高的特點，在工程上依然具有一定的使用價值。

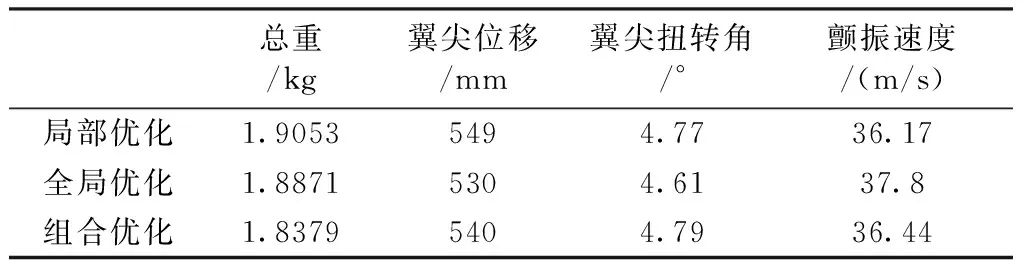
表8不同優化方法結果對比

組合優化結果與初始設計方案在相同工況下機翼Z方向的變形對比，如圖 13所示，可以得到優化后結構總體剛度顯著減小。顫振v-g圖如圖 14所示，可以得到機翼優化前顫振速度不滿足約束條件，通過優化設計使得顫振速度處于約束范圍內，顫振形式并未發生改變，屬于彎扭顫振，參與模態同樣是垂直一階彎曲、水平一階彎曲和一階扭轉的耦合。

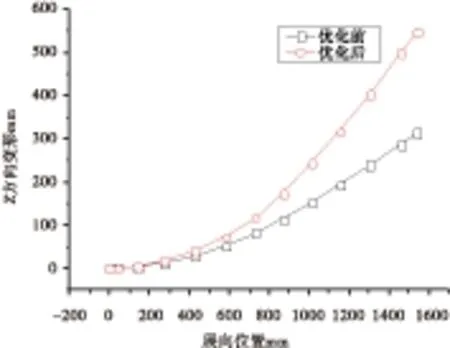
圖13組合優化變形結果對比

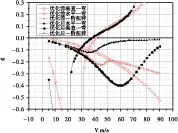
圖14組合優化顫振結果對比

4結束語

大變形產生的幾何非線性效應給傳統飛機設計理念和方法帶來了很大的挑戰。基于有限元和曲面氣動力建模方法，通過曲面樣條函數插值法實現位移和載荷信息的相互傳遞，將彈性力學幾何非線性理論引入到大柔性飛行器的氣動彈性力學分析當中，建立了完整的能夠考慮大變形的氣動彈性優化設計分析框架。結合優化算法和氣動彈性分析方法的特點，為了提高計算效率，有效簡化了迭代求解過程。從計算時間和優化結果來看，不僅提高了計算效率，而且保證了優化結果具有較高精度，滿足優化設計要求。基于ISIGHT優化平臺，采用直接搜索法HJ法，分別針對兩種變形算例，對機翼主梁剖面尺寸進行了優化設計。研究表明大展弦比機翼在氣動載荷作用下發生較大變形時，會對結構剛度產生影響，一般表現為結構頻率的降低，從而使得大展弦比機翼的臨界顫振速度降低，如果采用線性分析方法進行優化設計，會導致結果無法滿足真實工況下的性能指標，因此進行幾何非線性氣動彈性優化設計是十分必要的。為了同時發揮直接搜索法和蟻群算法的優勢，實現了兩種算法的有效組合，同時保證了全局性和精確性，相比于采用單一算法的優化策略，獲得了精度更高的設計結果，但是計算時間相對更長。

[1] 陳桂彬,鄒叢青,楊超.氣動彈性設計基礎[M].北京:北京航空航天大學出版社,2004.

[2] XIE C C,YANG C.Linearization method of nonlinear aeroelastic stability for complete aircraft with high-aspect-ratio wings[J].Science China Technological Sciences,2011,54(2):403-411.

[3] 王勖成,邵敏.有限單元法基本原理和數值方法[M].北京:清華大學出版社,1997.

[4] XIE C C,WANG L B,YANG C,et al.Static aeroelastic analysis of very flexible wings based on non-planar vortex lattice method[J].Chinese Journal of Aeronautics,2013,26(3):514-521.

[5] 管德.非定常氣動力計算[M].北京:北京航空航天大學出版社,1991.

[6] XIE C C,YANG C.Surface splines generaliza-tion and large deflection interpolation[J]. Journal of Aircraft,2007,44(3):1024-1026.

[7] 楊超.飛行器氣動彈性原理[M].北京:北京航空航天大學出版社,2011.

[8] LIU Y Q,LIU S Y,GU M T.Hooke and Jeeves algorithm for linear support vector machine[J].Journal of Systems Engineering and Electronics,2010,21(1):138-141.

[9] LEWIS R M,TORCZON V,TROSSET M W.Direct search methods:then and now[J].Journal of Computation and Applied Mathematics,2000,124(1-2):191-207.

[10] DORIGO M,STTZLE T.Ant Colony Optimization[M].Bradford:The MIT Press,2004.

[11] DORIGO M,MANIEZZO V,COLORNI A.Ant system:optimization by a colony of cooperating agents[J].IEEE Transactions on Systems,Man,and Cybernetics,1996,26(1):29-41.

[12] BULLNHEIMER B,HARTL R F,STRAU C.A new rank based version of the ant system;a computational study[J].Central European Journal for Operations Research and Economocs,1997,7(1):25-38.

Aeroelastic Optimization Design for High-aspect Ratio Wing Under Large Deformation

WANGFei1,LIQiuyan1,XIEChangchuan2,MENGYang2

(1.Chengdu Aircraft Design and Research Institute, Chengdu 610091, China; 2.College of Aeronautics Science and Engineering, Beihang University, Beijing 100191, China)

Aeroelastic problems are becoming increasingly prominent, which will have an important impact on the flight performance and safety indicators of aircrafts. It is the design needs of large transport aircrafts and high-altitude long-endurance unmanned aerial vehicle to study the aeroelasticity of large flexible aircraft during recent years. In the view of the problems, it proceeds as follows. Considering the structural large deformation, the geometric nonlinear elasticity theory is introduced into aeroelasticity analysis of flexible aircraft. Then the complete geometric nonlinear aeroelastic analysis framework is established. This method consists of two main areas. One is structural deformation stiffness and the other is the surface aerodynamic calculation. Combined with optimization, the iterative process of static and dynamic aeroelastic are simplified respectively in order to improve efficiency. Based on the ISIGHT optimization platform, a design method of high aspect ratio wing under large deformation is developed, which is suitable for the aeroelastic preliminary design phase. On the basis of geometric nonlinear aeroelastic analysis methods, direct search method is used for optimization. Combining the geometric nonlinear aeroelastic analysis methods and ISIGHT platform, the deviation caused by linear aeroelastic analysis under large deformation is effectively avoided. In order to get rid of dependence on the initial design point, the combination optimization strategy is used to carry on the nonlinear aeroelastic optimization design. Firstly the ant colony algorithm is used to locate the area of the target extreme value. Then the direct search algorithm is used to exactly optimize. At last better results are obtained.

aeroelasticity; large aspect ratio; geometrical nonlinearity; aeroelastic optimization design; direct search algorithm; ant colony algorithm

2016-04-06

王 斐(1988-),男,四川成都人,碩士,主要從事氣動彈性方面的研究,(E-mail)362049298@qq.com

1673-1549(2017)02-0042-07

10.11863/j.suse.2017.02.09

V211.47

A