類比思想在立體幾何中的應(yīng)用
■鄭州市第十一中學(xué)1805班 趙晨思
類比思想在數(shù)學(xué)中有著重要的應(yīng)用,下面舉例分析它在立體幾何中的應(yīng)用。
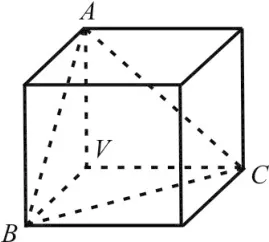
圖1
截正方形ABCD的一個角得△ABC,由勾股定理知c2=a2+b2。如圖1,把正方形換成正方體,截線AC換成截面ABC,得三棱錐V-ABC,設(shè) △VAB,△VBC,△VAC,△ABC面積分別為S1,S2,S3,S,則在棱錐V-ABC中有結(jié)論:S2=。

引用例1中的三棱錐V-ABC,VA、VB、VC與平面ABC所成的角分別為α、β、γ,三者有何關(guān)系?平面ABC與平面VAB、平面VAC、平面VAB的夾角分別為α1、β1、γ1,三者有何關(guān)系?
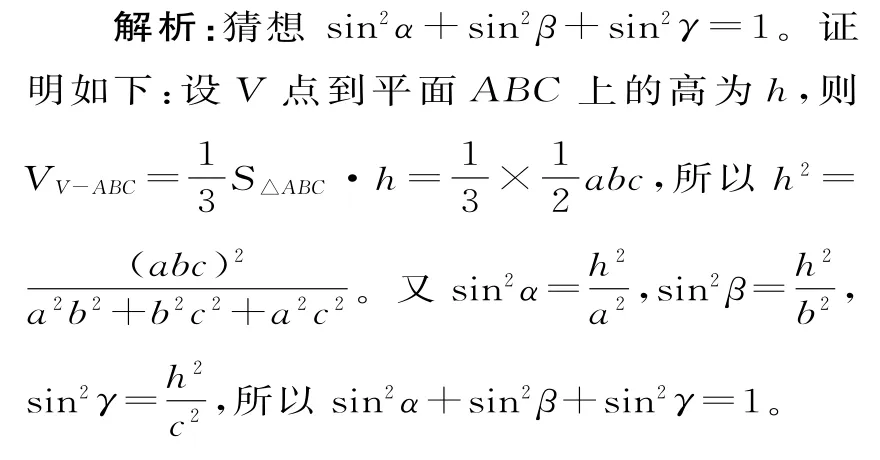
所以cos2α+cos2β+cos2γ=2。
那么,猜想sin2α1+sin2β1+sin2γ1=2。
證明如下:設(shè)△VAB邊AB上的高為VD,△VBC邊BC上的高為VE,△VAC邊AC上的高為VF。所以·AB=得VD2
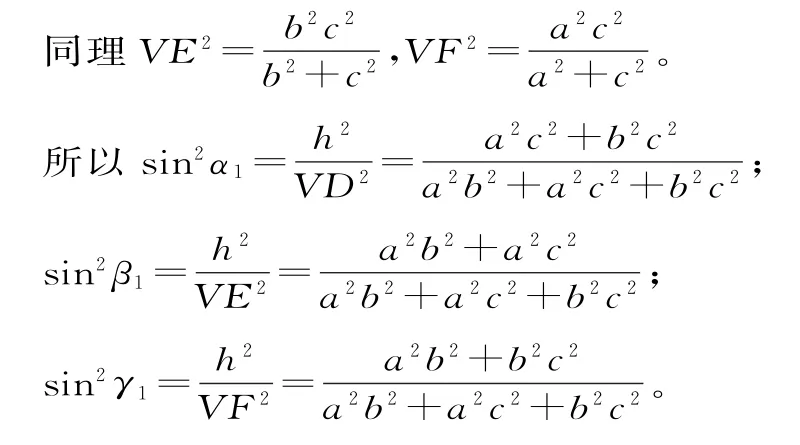
所 以 sin2α1+sin2β1+sin2γ1=2。
在長方體A1B1C1D1-ABCD中,A1B1=a,B1B=h,B1C1=b,體對角線B1D與從B1點發(fā)出的三條棱B1A1,B1B,B1C1的夾角分別為α、β、γ,三者之間有何關(guān)系?B1D與平面A1B1C1D1的夾角為α1,B1D與平面B1C1CB的夾角為β1,B1D與平面A1B1BA夾角為γ1,探究α1、β1、γ1的關(guān)系。
解析:猜 想 cos2α+cos2β+cos2γ=1,cos2α1+cos2β1+cos2γ1=2。
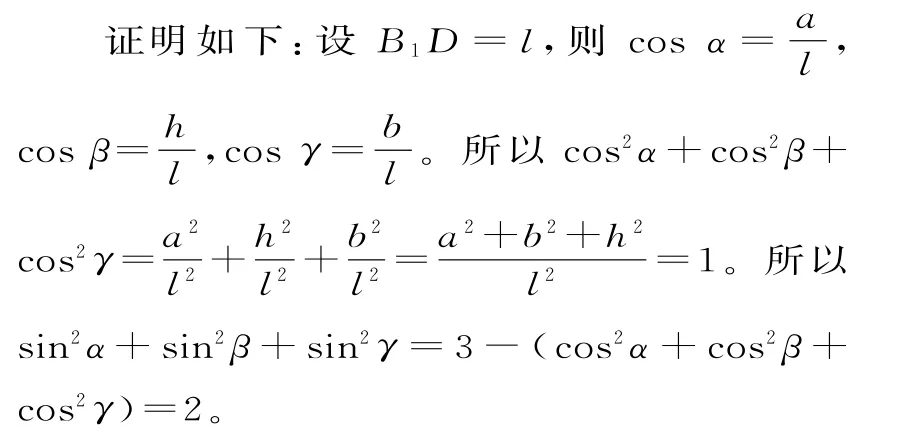
同理,猜想sin2α1+sin2β1+sin2γ1=1,cos2α1+cos2β1+cos2γ1=2。
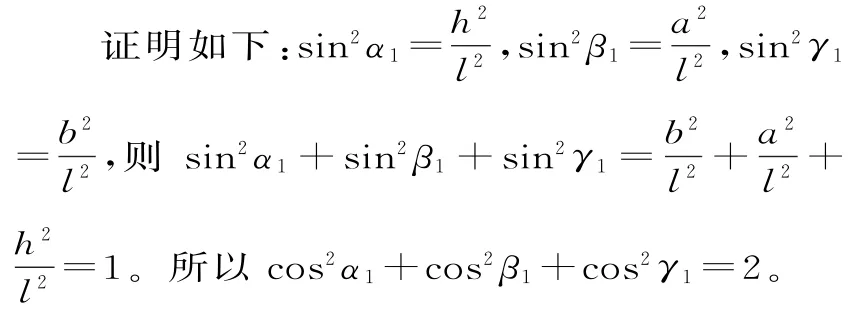
通過這三道例題,我們能夠深刻體會到類比思想在立體幾何中的應(yīng)用。
 中學(xué)生數(shù)理化(高中版.高二數(shù)學(xué))2017年12期
中學(xué)生數(shù)理化(高中版.高二數(shù)學(xué))2017年12期
- 中學(xué)生數(shù)理化(高中版.高二數(shù)學(xué))的其它文章
- 常用邏輯用語單元檢測題(B卷)參考答案
- 橢圓測試卷(A卷)參考答案
- 由一道最值問題談分式型柯西不等式的應(yīng)用
- 一道直線與橢圓有公共點問題的多種解法
- 聚焦高考中簡易邏輯的經(jīng)典問題
- 無處不在的充分必要條件
