星載激光測高系統誤差分析

王 昱，艾 宇，呂 源

1.西安測繪研究所，陜西 西安，710054;

2.地理信息工程國家重點實驗室，陜西 西安，710054;

3.西安航天天繪數據技術有限公司，陜西 西安，710054

1 引 言

自從1974年“阿波羅”登月飛船上首次使用激光測高技術以來，包括美國、日本、中國等國家先后開展了星載激光測高技術的研究工作，國內外已經發射的典型激光測高衛星及其基本技術參數見表1[1-3]。

表1 國內外已經發射的典型激光測高衛星基本技術參數

美國于2003年發射的ICESAT衛星搭載了GLAS傳感器，可測定沿軌道的陸地和水面的地形。由于GLAS獲取的各級激光測高數據可以公開下載，已成為國內外學者從事星載激光測高技術研究的首選數據源。

ICESAT官方公布了其對GLAS傳感器的高程確定精度分析結果，但沒有給出完整的描述星載激光測高系統定位誤差的數學模型。范春波[4]、朱劍鋒[5]等提出了激光腳點定位模型，并給出了主要的誤差源，但沒有對腳點定位模型和誤差源之間的關系進行理論分析。黃朝圍[6]等利用簡化模型分析了不同地形條件下星載激光測高精度的變化。馬躍[7]利用簡化模型分析了姿態對星載激光測高系統的影響，并利用南極地區的Li-DAR數據進行了高程精度檢驗試驗。唐新明等[8]推導了激光測高衛星嚴密幾何定位模型，并對光行差、硬件安裝誤差作了分析，但并未逐項分析激光測高的誤差影響。文獻[9-11]利用SRTM、機載LiDAR數據開展了針對GLAS數據的定位精度檢驗。

本文從星載激光雷達的精密幾何定位模型出發，推導了各主要誤差項對于激光雷達腳點幾何定位的誤差傳播方程，利用仿真數據模擬了不同設計參數和誤差條件下的定位誤差。試驗結果表明，姿態測量誤差、指向角測量誤差和距離測量誤差對定位精度的影響較為劇烈。從獲取滿足無控定位精度要求的激光控制點的角度分析，在600km軌道高度，激光測高儀姿態測量和指向角測量精度應至少優于1.5″，測距精度應優于0.25m。

2 星載激光嚴密定位模型

本文涉及的主要坐標系定義如下：地心慣性坐標系OICRF-XICRFYICRFZICRF采用國際大地測量協會和天文學聯合會于1984年啟用的協議天球坐標系J2000;地固系OITRF-XITRFYITRFZITRF是以地球質心為原點，Z軸指向地球的北極，X軸指向格林尼治子午線與地球赤道交點，Y軸則按照右手法則確定;衛星本體坐標系OBody-XBodyYBodyZBody是以衛星的質心為原點，Y軸沿著衛星橫軸，X軸沿著縱軸指向衛星飛行方向，Z軸按照右手法則確定;激光測高儀坐標系原點在測高儀質心，坐標軸與衛星本體坐標系平行。

星載激光測距的空間幾何關系如圖1所示。其中，圖1(a)表示衛星本體坐標系 OBody-XBodyYBodyZBody、激光光線以及激光地面足印點在地心慣性系OICRF-XICRFYICRFZICRF中的位置關系;圖1(b)則表示在激光測高儀坐標系中激光指向角θ、α的定義及其與激光腳點坐標的關系。在圖1(a)中，Olaser為激光發射的參考點;PGNSS為GNSS天線相位中心;OBody為衛星質心;Pground為激光地面足印點。星載GNSS測定的是GNSS相位中心的位置;姿態敏感器測定的是星敏在J2000坐標系下的指向。為了得到激光脈沖發射時的位置和姿態，需要將GNSS和星敏測定的數據轉化為激光測高儀的位置和指向，因此，需通過地面測定GNSS相位中心在衛星本體坐標系中3個偏移[Dx Dy Dz]T以及星敏感器本體系和衛星本體系之間的坐標旋轉關系。同時，激光測高儀相對衛星本體之間也需測定位置偏移[dx dy dz]T及脈沖發射指向與衛星本體坐標軸的角度旋轉之間的關系。

圖1 星載激光測高原理

如圖1(b)所示，假設激光指向與測高儀坐標系Z軸的夾角為θ，在XLaserOLaserYLaser平面上的投影OLaserC與 X軸正向夾角為α，ρ為激光的測距值，則激光腳點在衛星本體坐標系下的坐標為：

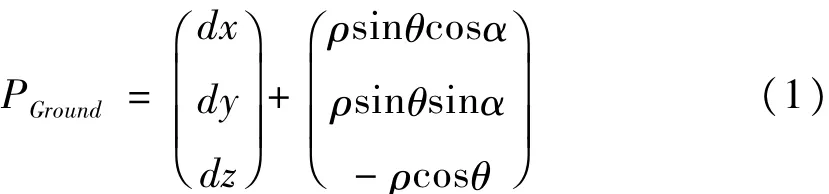
因此，在不考慮大氣折射影響的條件下，在地固系中的星載激光測高嚴密幾何定位模型為：

3 激光足印點定位誤差源分析

對(2)式進行分析可以看出，激光足印點的定位精度主要受以下幾項誤差因素的影響：

一是衛星的質心定位誤差，由星載GNSS接收機本身的定位誤差以及內插計算引起。該項誤差與其引起的定位精度變化是線性關系，影響有限。

三是激光測高儀的安置誤差，包括GNSS偏心誤差、激光參考點偏心誤差、激光指向角誤差三部分內容。其中兩項偏心誤差在實驗室環境下的測定精度較高，盡管衛星在軌后會產生一定的變化，但其影響仍然相對較小。相比較而言，激光指向與衛星本體系的角度測量誤差由于受測距值放大效應的影響會帶來較大的誤差，因此，是分析的重點。

四是激光測高儀的測距誤差，主要為激光測高儀硬件測距誤差和激光穿越大氣層引起的傳輸誤差，其中硬件測距誤差可以通過標定和測量消除，傳輸誤差可以通過后期處理修正。

因此，本文對于激光腳點誤差的分析主要圍繞位置定位誤差 mXs、mYs、mZs，姿態測量誤差 mφ、mω、mκ，指向角測量誤差 mθ、mα和測距誤差 mρ9個變量展開。假設上述9個變量取值相互獨立，則對(2)式進行泰勒展開，取一次項得到(3)式。(3)式可以作為激光測距儀定位的誤差傳播方程，用于分析各誤差項以及衛星設計值對于激光測高精度的影響。由于定位誤差的影響有限，因此，下面重點分析姿態測量誤差、指向角測量誤差以及測距誤差對激光腳點定位精度的影響。

3.1 姿態測量誤差

姿態測量誤差主要是衛星在軌運行時星敏、陀螺等儀器測量衛星姿態時產生的誤差，可以分為俯仰φ、側滾ω以及偏航κ三個正交方向的角誤差分量。

對(2)式求偏導，可得

3.2 指向角測量誤差

正如前文所述，在安置誤差中，由于GNSS和激光測高儀的偏心誤差影響較小，而指向角誤差受測距值影響對腳點定位精度產生的影響較大，因此，本節重點分析指向角誤差。

分析(2)式可以看出，旋轉矩陣A中的變量只和姿態角以及坐標系轉換參數有關，和θ以及α角度即指向角無關。對(2)式求偏導可得，激光指向與激光測高儀本體坐標系Z軸夾角θ引起的誤差可表示為：

激光在XOY平面上的投影與X軸正向夾角α引起的誤差可表示為：

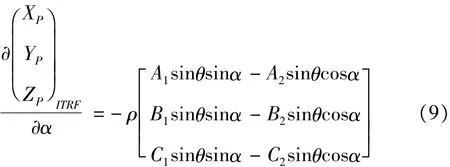
3.3 距離測量誤差

星載激光測高儀的測距系統誤差雖然在地面進行了嚴格的實驗測定，但是入軌后其性能可能會受到影響。總的來講，距離測量誤差主要包括時間同步誤差、地形起伏引起的定位誤差及大氣傳輸誤差等，距離測量誤差對激光腳點定位誤差的影響可表示為：

4 試驗分析

為了系統分析衛星設計參數和定標誤差對腳點定位精度的影響，參考ICESat及國內外同類衛星的設計使用情況，簡化了公式(3)的分析條件，假設衛星質心及天線相位中心偏移量均為0，且在衛星飛行過程中，衛星姿態較為穩定，均為接近于0的微小角度，故將姿態角均設為0°。在同等測量誤差情況下，飛行高度對定位精度的影響，近似認為，在此條件下，整理(3)～(10)式，得到三軸的誤差傳播方程如(11)式所示

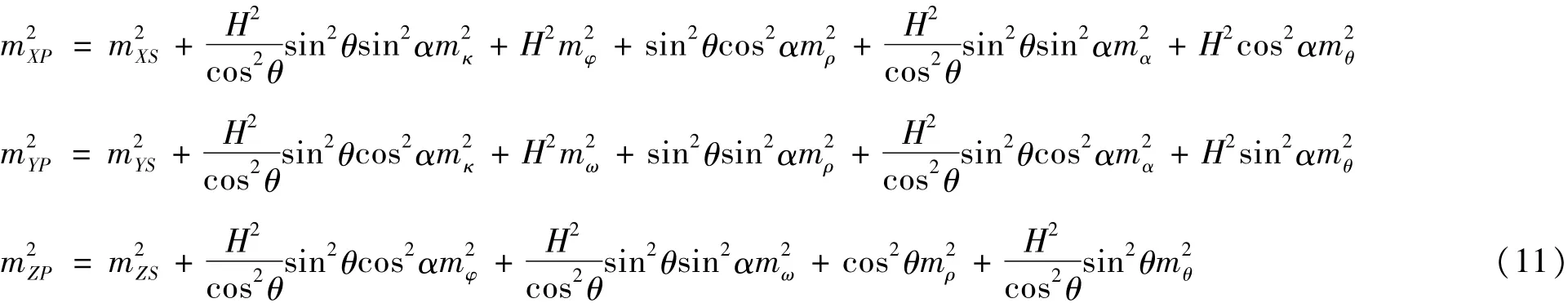
針對(11)式，重點分析衛星設計指標包括飛行高度H和指向角θ，以及測量誤差包括平臺定位誤差、姿態測量誤差、指向角測量誤差以及測距誤差對腳點定位精度的影響。

從衛星應用的角度分析，受星上能源條件限制，目前激光測高衛星獲取的控制點密度還無法滿足地形測量中DEM獲取的密度要求，激光測高衛星獲取的控制點或測距數據的用途主要是滿足大比例尺測圖中的精度提升需要，通過深入分析文獻[12]提出的1：1萬無控測圖過程中的激光控制數據應用需求，在本文的仿真試驗中，將激光控制點的精度要求設定為平面10m、高程1m。另外參考ICESat設計指標，除特別說明外，衛星飛行高度均為600km，指向角θ為0.3°，指向角α為90°，相關測量誤差的取值考慮了國內外測距儀制造標定的平均水平，具體見表2。

表2 測量誤差的取值

4.1 衛星設計指標對腳點定位精度的影響

在各項測量誤差不變的情況下，試驗中分別改變軌道高度和指向角的設計參數，考察腳點定位誤差變化對X、Y、Z三軸方向的誤差 MX、MY、MZ以及總的定位誤差MXYZ的影響情況。具體試驗結果見表3和表4，其變化分析如圖2和圖3所示。

表3 飛行高度對定位精度的影響(m)

表4 指向角θ對定位精度的影響(m)

圖2 飛行高度的影響

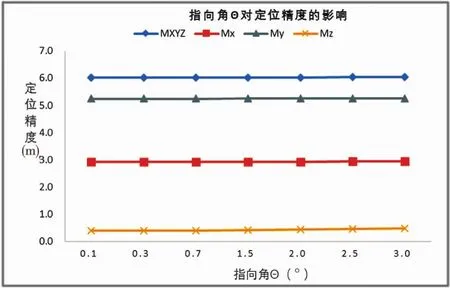
圖3 指向角θ的影響

從表3和圖2可以看出，在相同誤差條件下，降低飛行高度，定位誤差隨之線性減小，這說明適當降低飛行高度有助于降低各項誤差的影響。三軸方向的誤差相互比較，平面X、Y方向變化較為劇烈，而Z方向則較為平緩，衛星高度從800km降至200km，Z方向誤差僅減小了不到2cm。

分析表4和圖3可以看出，相比飛行高度，指向角θ對定位誤差的影響則相對較小，θ由0.1°提高到3°，總的定位誤差值提高了約4cm。分析原因主要是指向角θ通過三角函數對定位誤差產生影響，影響幅度有限。

指向角α對定位精度的影響見表5。仿真分析表明，該項設計值雖然對X、Y、Z方向的定位精度產生影響，但總的定位誤差則沒有發生明顯變化。

表5 指向角α對定位精度的影響(m)

4.2 測量誤差對于腳點定位精度的影響

各項測量誤差中，平臺位置測量誤差的影響最簡單，從(11)式可以看出，其對腳點定位精度的影響不僅是線性的，而且處在一個數量級上，圖4的仿真結果也印證了上述結論。下面重點分析一下姿態測量誤差、測距誤差以及指向角測量誤差的影響。

(1)姿態測量誤差的影響

在其他條件不變的情況下，將姿態測量誤差的取值由3″降到0.2″，腳點定位誤差的變化情況見表6和圖5?？梢钥闯?，隨著姿態測量誤差的減小，腳點定位精度迅速提升，特別是在X、Y方向變化非常顯著，這種現象出現的原因主要是姿態測量精度影響了激光發射方向的確定精度，從而對腳點的平面定位精度產生了影響。從目前激光腳點10m的平面定位精度要求，并考慮一定富裕量，姿態測定精度應優于1.5″。

表6 姿態測量誤差的影響(m)

圖4 平臺定位誤差的影響

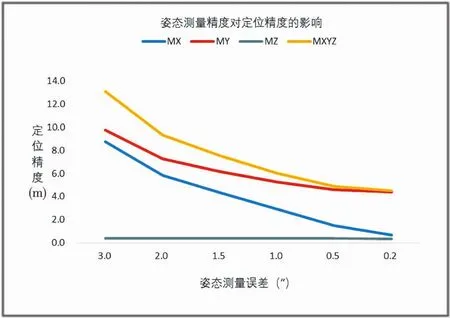
圖5 姿態測量誤差的影響

(2)測距誤差的影響

在其他條件不變的情況下，將測距誤差由1m縮小到0.05m，定位誤差的變化見表7和圖6?？梢钥闯觯瑴y距誤差主要對Z方向的定位誤差構成影響，且非常顯著。應該指出在本次試驗中，測距誤差對于Y方向定位精度也有影響，因為發生在小數點6位以后，因此，在表6中沒有顯示出來，隨著姿態確定誤差的減小Y方向定位精度也不斷提升。從目前對于激光控制點1m的高程定位精度要求并考慮激光測高儀的技術發展水平，測距誤差應小于0.25m。

圖6 測距誤差的影響

圖7 指向角測量誤差的影響

(3)指向角測量誤差的影響

改變指向角θ的取值，由5″變化至0.5″，腳點誤差的變化見表8和圖7。可以看出，指向角對定位誤差的影響類似于姿態測量誤差的影響，主要影響平面定位精度，對Z方向的精度也有影響，但影響有限。至于影響X方向還是Y方向或者均影響，取決于α的取值。從滿足目前激光控制點10m平面定位精度的要求并考慮指向角地面標定技術的發展，指向角測量精度應優于1.5″。

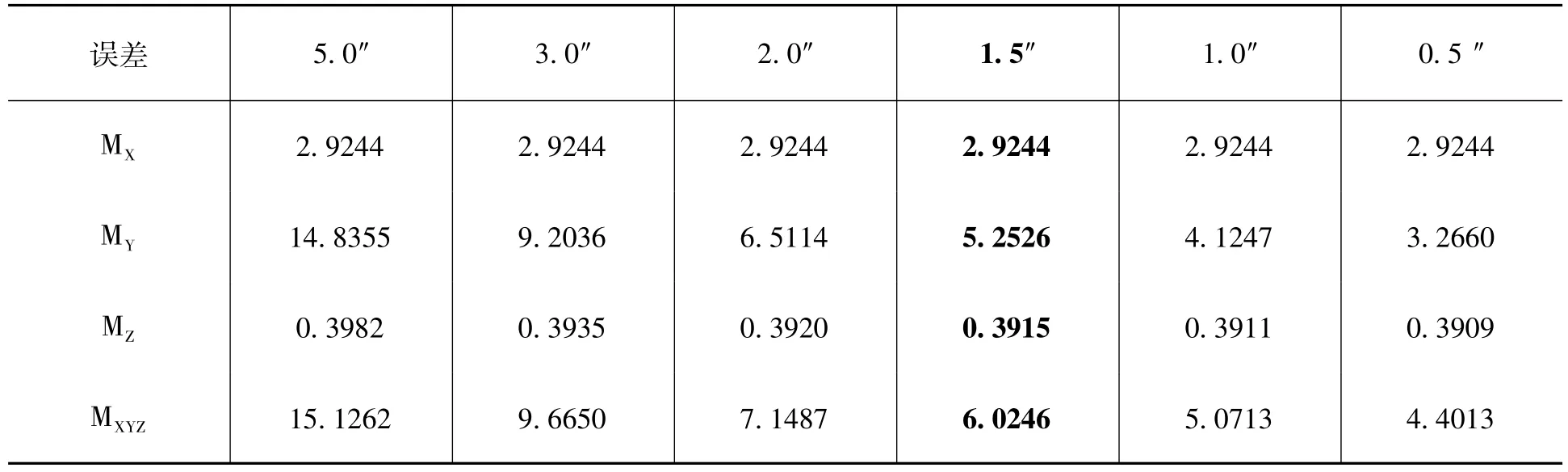
表8 指向角誤差的影響(m)

應該指出姿態測量誤差小于1.5″，測距誤差小于0.25m，指向角測量誤差小于1.5″的結論都不是單項誤差獨立影響的結果，而是在如表2所示的缺省誤差條件(此時姿態測量精度1.0″)下得出的。事實上綜合表6～8可以看出，當使用缺省誤差條件時(字體加粗)，三軸總的測量精度優于6.03m，平面定位精度優于6.02m，高程定位精度優于0.40m。在表6中還仿真了姿態測量精度1.5″，其他誤差處于缺省條件的總的誤差(表6中第四列字體加粗)，其中三軸測量精度優于7.58m，平面定位精度優于7.57m，高程定位精度優于0.40m。

4.3 不同方向精度影響差異性的討論

總結4.1、4.2節的試驗不難看出，同樣的誤差，對于X、Y、Z三個方向精度影響有較大差異，除測距誤差外，姿態測量誤差、指向角測量誤差對于X、Y方向定位精度影響較大，對于Z方向精度影響不大。為了分析造成這種影響的原因，選定一組典型參數 H=600km，θ =0.3°，α=90°，代入公式(11)得到：

從(12)式可以看出飛行高度與測距值成正比，而飛行高度對于姿態和指向角測量誤差的放大作用主要體現在X、Y方向(例如對于mω，影響因子是600000)，對于 Z方向的影響相對較小(mω的影響因子3141.62)，這就是Z方向精度變化小于X、Y方向的原因。同樣測距誤差的影響因子X、Y方向要遠小于Z方向，這也解釋了測距誤差對于Z方向影響大于X、Y方向的原因。

同時仔細觀察一下公式(11)會發現，除平臺定位誤差外，姿態誤差、指向角誤差以及測距誤差在X和Y方向均關于角α成正余弦對稱關系，如果在X方向誤差因子中有sinα，則在Y方向誤差因子中必然有cosα。其實回顧一下圖1(b)中α的定義就會發現，這種規律的產生有其必然性，因為α本來就是用來定義激光光線在X、Y軸上的投影的。由于α取值一般是0°或90°，因此，各誤差項對于X、Y的影響也成對稱關系。例如當α=90°時，對X方向定位精度產生影響的誤差項是mφ、mκ、mα，對 Y方向定位精度產生影響的誤差項是 mω、mρ、mθ，這種對稱現象在表5中得到了充分體現。隨著α的變化X方向和Y方向的精度變化呈現此消彼長的特點，同時總的誤差則幾乎不變，這也解釋了為什么在表7中指向角θ的誤差只對Y方向精度產生影響。

5 結 論

本文從星載激光測高儀的嚴密定位模型出發，推導了各主要誤差源的誤差傳播方程，利用仿真試驗分析了各種誤差源對于定位精度的影響。從試驗結果看，姿態測量誤差、指向角測量誤差和測距誤差對定位精度的影響較大。其中，姿態測量誤差和指向角測量誤差主要影響激光腳點的平面定位精度;測距誤差則對高程定位精度的影響較為明顯。

從滿足衛星設計研制的角度分析，在激光測高儀技術狀態確定的情況下，適當降低飛行高度有利于提高定位精度。在600km軌道高度激光測高儀如果需要滿足平面10m、高程1m的定位精度，激光測高儀的姿態測量精度和指向角測量精度應至少優于1.5″，測距精度應優于0.25m。本次研究中，還未考慮地形坡度對于定位精度的影響，后續將開展深入研究。

[1]文漢江，程鵬飛.ICESAT/GLAS激光測高原理及其應用[J].測繪科學，2005，30(5)：33-35.

[2]王建宇，舒嶸，陳衛標等.嫦娥一號衛星載激光高度計[J].中國科學，2010，40(8)：1063-1070.

[3]韓玲，田世強，謝俊峰.星載激光測高儀檢校技術發展現狀淺析[J].航天返回與遙感，2016，37(6)：11-19.

[4]范春波等.ICESAT/GLAS激光腳點定位及誤差分析[J].大地測量與地球動力學，2007，27(1)：104-106.

[5]朱劍鋒，王昱，胡煜等.星載激光測高的系統誤差分析與檢校[J].測繪通報，2014(S1)：137-140.

[6]黃朝圍，李國元，李姍姍等.不同地形條件下的星載激光測高系統誤差分析[J].測繪科學，2016，41(1)：44-49.

[7]馬躍，陽凡林，盧秀山等.對地觀測星載激光測高系統高程誤差分析[J].紅外與激光工程，2015，44(3)：1042-1047.

[8]唐新明，李國元，高小明等.衛星激光測高嚴密幾何模型構建及精度初步驗證[J].測繪學報，2016，45(10)：1182-1191.

[9]艾建華.利用 ICESAT/GLAS激光測高數據評估SRTM數據精度[J].測繪技術裝備，2015，17(2)：63-66.

[10]Hieu Duong.Icesat Full-waveform Altimetry Compared to Airborne Laser Scanning Altimetry Over The Netherlands[J].IEEE Transactions on Geoscience and Remote Sensing，2009，47(10)：3365-3378.

[11]Lori A，etc.ICESATAltimetry Data Product Verification atWhite Sands Space Harbor[J].IEEE Transactionson Geoscience and Remote Sensing，2007，45(1)： 149-155.

[12]王任享.中國無地面控制點攝影測量衛星追述(二)1：1萬傳輸型攝影測量衛星技術思考[J].航天返回與遙感，2014，35(2)：1-5.