基于SPSO的PID參數自整定速度控制

孫 波,魏 勇,楊觀賜

(1.河南工學院,新鄉453003;2.貴州大學,貴陽550003)

0 引 言

感應電機具備自由變速控制、耐用性高、低成本、可靠性強等優點,在工業領域被廣泛應用[1]。為了滿足高端工業領域的控制需求,感應電機驅動系統需要具備較寬的轉速和扭矩控制范圍、高效率且快速的轉矩響應等性能特征[2]。

感應電機的控制方式主要為轉子磁場定向控制(以下簡稱 FOC)[3]和直接轉矩控制(以下簡稱DTC)[4]。這些控制架構中的速度閉環控制模塊是整個系統的核心部分,其決定著后續磁通和轉矩的控制性能。速度閉環控制通常采用比例積分微分(以下簡稱PID)控制器[5]。然而,傳統PID控制器在不同操作條件下的參數值設定不變,不能實現轉速的高穩定性[6]。為此,出現了一些融合先進技術的改進型PID,例如模糊PID參數自整定控制器[7],基于遺傳(以下簡稱GA)算法、粒子群優化(以下簡稱PSO)[8]等復雜進化算法的PID參數自整定控制器。但這些控制器都具有較大的計算量和計算時間,不能很好地滿足電機控制系統的實時性。

為此,本文提出了一種基于簡化粒子群優化(以下簡稱SPSO)算法自整定PID參數的速度控制器(以下簡稱SPSO-PID)。利用SPSO算法自適應調優PID參數,同時融入動態慣性權重來提高SPSO的搜索能力。實驗結果表明,提出SPSO算法能夠快速收斂到最優,從而使SPSO-PID控制器能夠快速且準確地控制電機速度,且對負載轉矩變化具有較好的魯棒性。

1 感應電機的數學模型

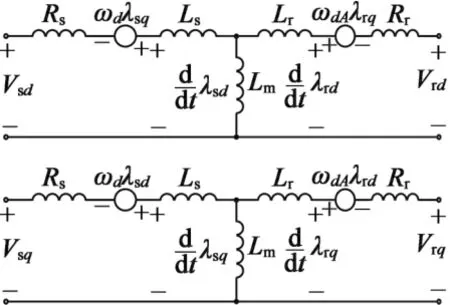
圖1 d-q坐標系下的感應電機等效模型

感應電機可以等效成同步旋轉d-q坐標系下的等效電路模型[9],如圖1所示。感應電機模型可用于預測驅動磁鏈、轉矩和速度到期望值的電壓,然后基于空間矢量調制來合成該電壓,以此實現電機的控制。d-q坐標系中,定子電壓和轉子電壓的表達式:

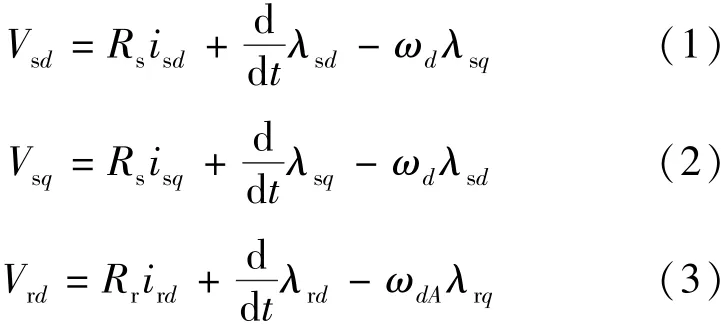
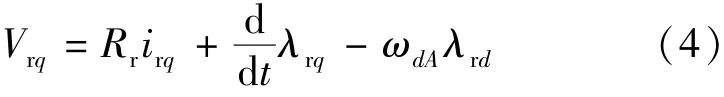
式中:Vsd和Vrd為d軸定子和轉子電壓;Vsq和Vrq為q軸定子和轉子電壓;Rs,Rr為定子,轉子電阻;isd,isq,ird,irq為定子或轉子的 d,q 軸電流;λsd,λsq,λrd,λrq為定子或轉子的d,q軸磁鏈。

本文中,研究對象為鼠籠式感應電機,其磁鏈與電流的關系表示:

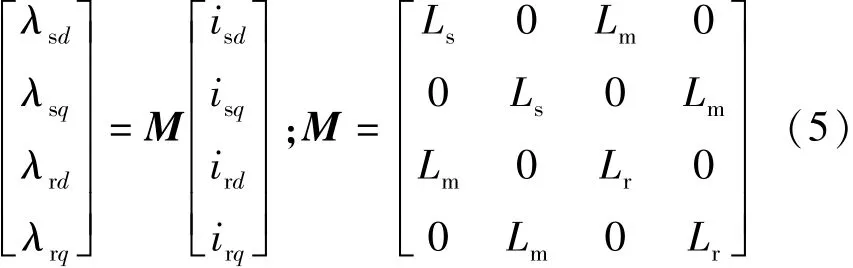
根據式(1)～式(5),則感應電機的電氣部分可由一個四階狀態空間模型來描述,表示如下:

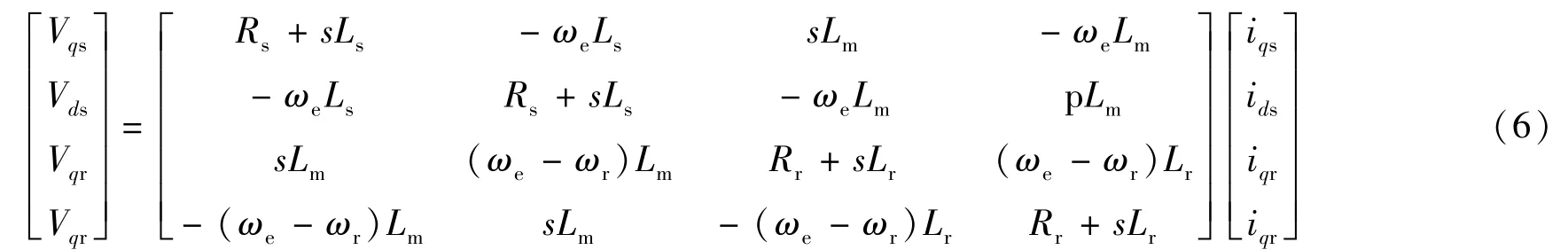
式中:s為拉普拉斯算子;p為微分算子。增加轉矩到轉子繞組的軸和q軸上時,所產生的瞬時轉矩表示:

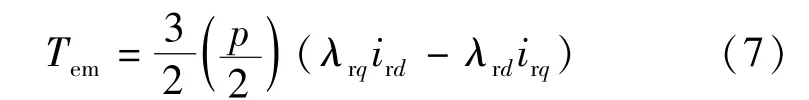
將瞬時轉矩轉換成以電感表示:

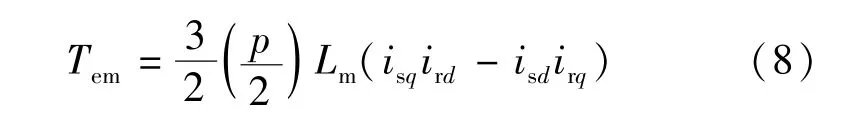
那么,電機的機械部分可建模:

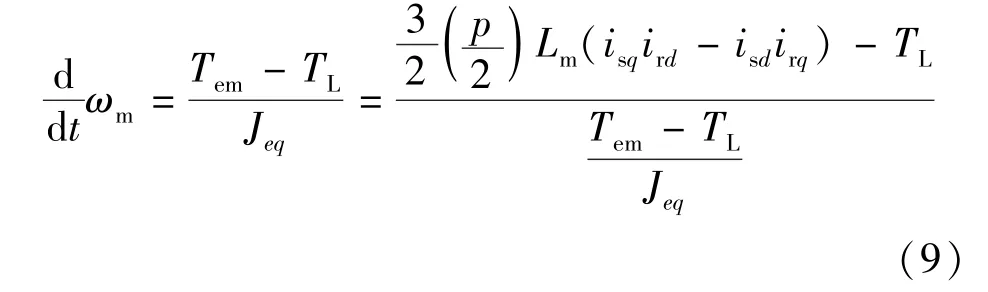
式中:ωm為角速度;Tem為電磁轉矩;TL為負載轉矩;Jeq為等效轉動慣量;Lm為互感;Lr為轉子電感;Ls為定子電感。

2 SPSO-PID速度控制器

2.1 SPSO-PID控制器架構

在感應電機控制中,通常采用基于同步旋轉(dq)參考坐標系的FOC框架,如圖2所示。對于轉矩控制,首先比較電機的設定參考速度(命令)與電機實際速度,獲得速度差信號,并輸入到速度控制器。然后,速度控制器產生驅動器q軸上的參考電流。將實際反饋的q軸電流與參考電流進行比較,生成相應的電流差信號。根據這個電流差信號,轉矩PI調節器生成轉矩電壓命令。同樣,勵磁控制和轉矩控制過程類似,生成勵磁電壓命令v。最后,將這些電壓信號轉化為靜止坐標系的電壓v和v,并以此產生脈寬調制來控制電機[10]。

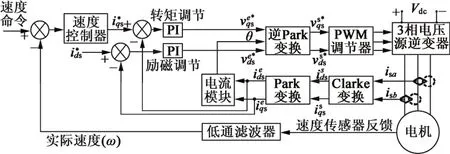
圖2 感應電機的FOC系統框架

可以看出,速度控制器是整個系統的核心部分,其決定著后續轉矩和勵磁的控制性能。通常速度控制器采用傳統PID控制,但其參數不能自適應調整。為此,提出了基于SPSO算法自整定PID參數的速度控制器。

在提出的SPSO-PID速度控制器中,將PID控制器的3個參數KP,KI和KD編碼為SPSO中的粒子。根據設定速度和反饋速度計算速度的平方誤差積分(ISE),并以此作為粒子的適應度函數。然后執行尋優過程獲得最優PID參數,實現速度的最優控制。SPSO-PI速度控制器框架如圖3所示。

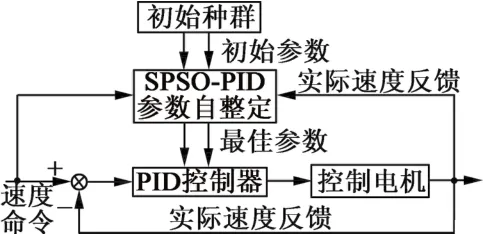
圖3 SPSO-PID速度控制器架構

2.2 SPSO算法

PSO算法是一種源于對動物群體覓食行為進行模擬的全局優化算法。其基于從全局最優解和當前最優解的信息來更新每個粒子的位置,使其在每次迭代中都會向吸引子所引導的方向移動,最終獲得最優解。粒子的速度和位置更新公式[11]:

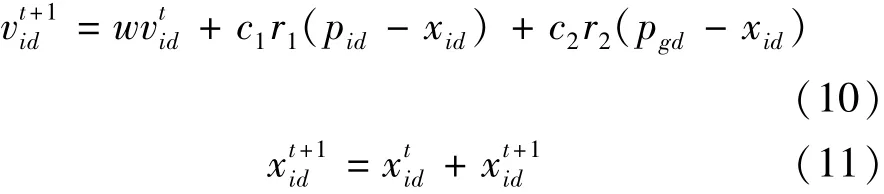
式中:i=1,2,…,N,N為j維粒子數;xid表示第i個粒子在第d維的當前位置;vid表示速度向量;pid和gid分別表示全局最優解和當前最優解;c1為認知參數,c2為社會參數;通常設置c1=c2=2;r1()和r2()是0和1范圍內的隨機數;w為慣性權重,決定對當前粒子速度的繼承程度,通常設置為0.8。

與其他全局尋優算法(遺傳算法、蟻群算法等)相比,PSO具有較優的全局尋優能力。然而,這些算法的計算時間相對較長,不能很好地應用在電機PID速度控制器參數的實時調整中。

文獻[12]通過分析生物模型和進化迭代過程,發現PSO的進化過程與粒子速度無關。另外,粒子速度的大小并不代表粒子能夠有效趨近最優解位置,反而可能造成粒子偏離正確方向,延緩后期收斂速度。為此,其將PSO進行改進,去掉了速度項,形成一種簡化粒子群優化(SPSO)算法。簡化后的粒子位置方程:

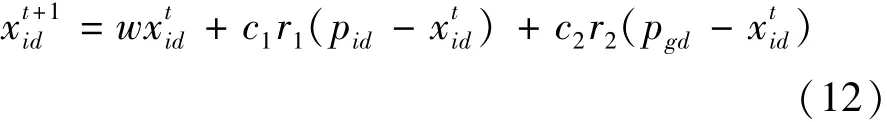
可以看出,簡化后的PSO位置方程由二階降到了一階,大大簡化了粒子進化過程和時間復雜度,使其能夠應用于電機PID速度控制器中。

另外,w設置為固定值不能適應動態的收斂過程。為此,本文引入了動態慣性權重,使其在一定范圍內,隨著迭代次數的增加而線性遞減,表達式如下:

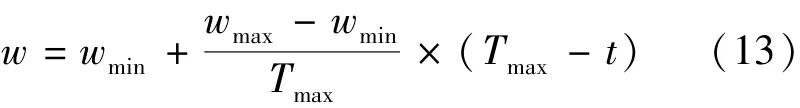
式中:wmax和wmin為w的最大值和最小值,取值為0.9和0.4;Tmax為最大迭代次數,t為當前迭代次數。

2.3 適應度函數

為了獲得最優PID控制器參數,需要設定優化算法的優化目標。常見的性能標準有[13]:絕對誤差積分(IAE)、平方誤差積分(ISE)、時間乘平方誤差積分(ITSE)和時間乘絕對誤差積分(ITAE)。為了選擇合適的適應度函數,在速度控制過沖、上升時間、穩定時間和穩態誤差方面進行比較實驗。結果表明,將ISE作為適應度函數時,控制系統綜合性能較好。為此本文采用ISE為目標函數,其表達式:

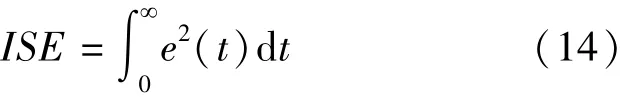
式中:e(t)為設定速度與實際速度的誤差。

3 仿真及分析

3.1 仿真設置

利用MATLAB/Simulink工具構建仿真實驗環境,仿真中構建了一個額定功率為3 kW、額定電壓為380V、額定轉速為1 200 r/min、極對數為2、定子電阻為2.3 Ω、轉子電阻為1.55 Ω、定子和轉子電感為0.261 H、互感為0.249 H、轉動慣量為0.02 kg·m2的三相感應電機。另外,在SPSO-PID控制器中,設置PID控制器的3個參數KP,KI和KD的搜索空間分別為[0,20],[0,1]和[0,1];SPSO算法的種群數量N=30,最大迭代數量Tmax=50。

3.2 SPSO收斂性分析

在相同參數設置下進行尋優實驗,執行100次迭代,比較帶動態慣性權重的 SPSO算法和傳統PSO算法的收斂性,結果如圖4所示。

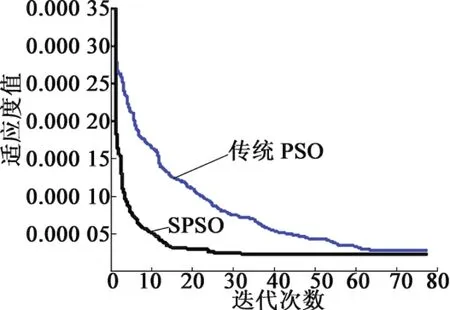
圖4 兩種PSO算法的收斂曲線

可以看出,與傳統PSO算法相比,帶動態慣性權重的SPSO算法的收斂速度很快,大約在25次迭代后就收斂到最優值,而傳統PSO大概需要70次迭代才能收斂。另外,SPSO所獲得最優解略優于傳統PSO算法。這是因為融入了動態慣性權重,在迭代開始時,賦予較大的w值,使其在全局范圍內快速搜索;而在迭代后期,賦予較小的w值,使其能夠在最優點附近精細搜索,不僅能夠加快收斂速度,還能夠提高收斂精度。所以,在提出的SPSO-PID速度控制器中,為了在保證最優收斂下提高時效性,設置最大迭代次數為50。

此外,由于SPSO算法去掉了速度項,每次迭代的時間也得到有效降低。

3.3 電機起動實驗

設置感應電機在t=0時從靜止狀態起動,速度設置為1 000 r/min,負載轉矩為空載,執行速度控制實驗。

此時,電機磁通、定子電流和電磁轉矩的響應曲線分別如圖5～圖7所示。可以看出,電機磁通、定子電流和電磁轉矩曲線基本在0.25 s后達到穩定狀態,且穩態時波動很小。

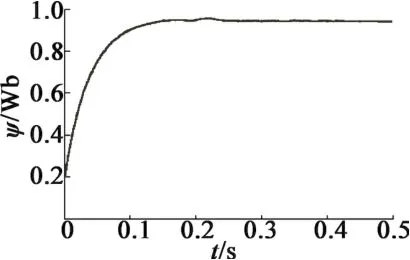
圖5 磁通響應曲線

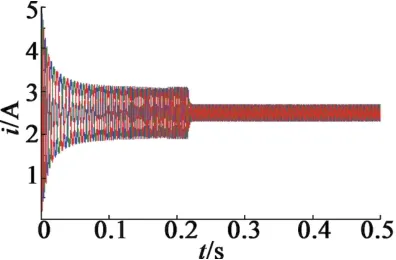
圖6 定子電流響應曲線

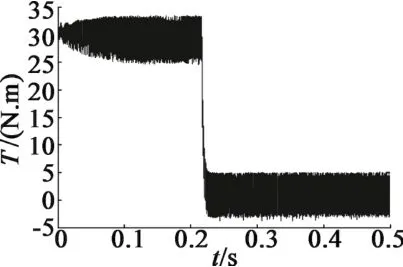
圖7 轉矩響應曲線

另外,電機起動時的轉子速度響應曲線如圖10(a)所示,和上述結果一致,在0.25 s內基本穩定到設定速度,且沒有超調現象。為了進行比較,在同樣場景下,利用傳統PID和文獻[7]提出的模糊PID速度控制器進行控制速度,其結果如圖10(b)、圖10(c)所示。可以看出,傳統PID控制器大約需要2 s才能穩定轉速,且存在很大的超調現象。模糊PID速度控制器大約需要1 s才能穩定速度,也存在一定的過沖超調現象。

3.4 電機負載變化實驗

設置感應電機在t=0時從靜止狀態起動,速度設置為1 000 r/min,負載轉矩為空載。然后,在t=3 s時施加負載TL=20 N·m。

圖8～圖9分別給出了電機定子電流和電磁轉矩響應曲線。可以看出,當負載變化時,控制器能夠快速調節定子電流和轉矩來穩定電機速度。

圖8 定子電流響應曲線

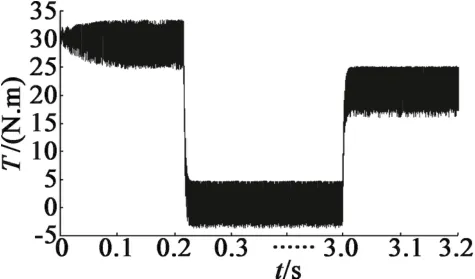
圖9 轉矩響應曲線

同樣,將提出的SPSO-PID控制器與傳統PID控制器、模糊PID控制器進行比較,結果如圖10所示。可以看出,在負載變化時(t=3 s),SPSO-PID控制器的速度變化很小,且能夠很快恢復到設定值。而傳統PID控制器的速度變化很大,且調整速度較慢。模糊PID控制器的速度控制性能優于傳統PID,但也存在速度波動情況。

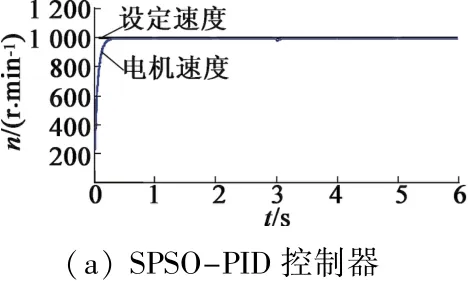
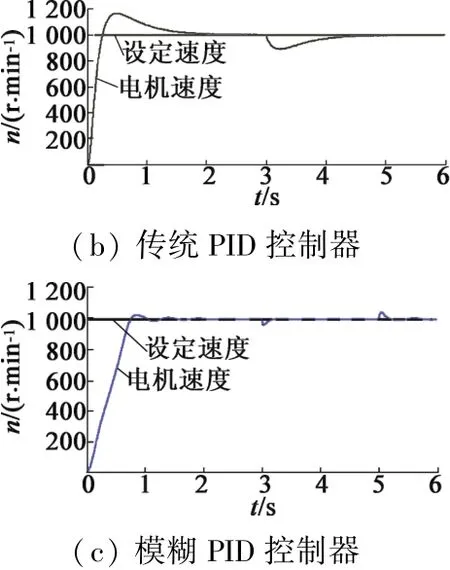
圖10 3種不同PID控制器的速度響應曲線

綜上分析表明,SPSO-PID控制器能夠快速地控制速度到設定值,且能夠對負載變化具有較強的魯棒性。

4 結 語

為了提高感應電機FOC系統中的PID速度控制器的性能,提出了一種SPSO-PID控制器。利用帶動態慣性權重的SPSO算法來優化PID參數,使其能夠快速且穩定地控制電機速度。由于SPSO去掉了粒子速度項,大大縮短了計算時間,所以能夠較好地滿足電機實時控制要求。在負載變化場景下的仿真結果證明了SPSO-PID控制器的可行性。

今后的工作中,將在實際感應電機中對SPSOPID控制器進行測試,以驗證其實用性。

[1] 李洪亮,姜建國.非正交坐標系下雙三相感應電機SVPWM控制策略[J].電機與控制學報,2014,18(12):17-23.

[2] 耿乙文,周勤奮,鮑宇,等.基于疊加復調節器的雙三相感應電機控制系統[J].中國電機工程學報,2015,35(13):3426-3435.

[3] 張岳,沈建新.雙三相感應電動機矢量控制調速系統建模與仿真[J].微特電機,2014,42(7):61-65.

[4] ALNASIR Z A,ALMARHOON A H.Design of direct torque controller of induction motor(DTC)[J].International Journal of Engineering&Technology,2012,4(2):23-29.

[5] 何基都,鄭永軍,譚彧,等.異步電機模糊免疫PID矢量控制系統[J].電機與控制應用,2013,40(5):13-15.

[6] SEKHAR O C,SEKHAR K C.Space vector modulation&fuzzy PID speed controller for direct torque control induction motor drive[J].2012,23(3):126-134.

[7] VENGATESAN V,CHINDAMANI M.Speed Control of three phase induction motor using fuzzy logic controller by space vector modulation technique[J].International Journal of Advanced Research in Electrical,Electronics and Instrumentation Engineering,2014,3(12):13650-13656.

[8] 張朝龍,江巨浪,江善和,等.一種基于改進PSO算法的PID控制器參數整定方法[J].化工自動化及儀表,2010,37(12):15-18.

[9] 李志鑫.基于空間矢量控制的雙PWM型感應電機變頻調速系統的研究[D].廣州:華南理工大學,2011:31-32.

[10] 楊云森,唐娟,任曉剛,等.基于DSP的異步電動機轉子磁鏈定向控制系統[J].微特電機,2015,43(1):65-66.

[11] BANERJEE T,CHOUDHURI S,BERA J,et al.Off-line optimization of PI and PID controller for a vector controlled induction motor drive using PSO[C]//International Conference on Electrical and Computer Engineering.IEEE,2011:74-77.

[12] PEDERSEN M E H,CHIPPERFIELD A J.Simplifying particle swarm optimization[J].Applied Soft Computing,2010,10(2):618-628.

[13] 于明莉.PID控制器確定性性能評價研究[D].大連:大連理工大學,2015.