關于開放小區對道路通行影響的研究

劉瑞+孫芳繽+陳家琦

摘 要：封閉式住宅小區的開放已成潮流，在這樣的背景下，有必要分析開放后的小區能否實現優化路網結構，提高道路通行能力的目標。該文主要研究了開放小區對道路通行的影響的定量分析方法，研究了小區的開放視為交通均衡模型類的新建道路問題，并且增加對道路結構和小區結構的考慮，以針對開放小區對道路通行影響進行研究。

關鍵詞：交通流均衡模型 差方和公式 優化模型

中圖分類號：F540 文獻標識碼：A 文章編號：1672-3791（2017）03（a）-0255-02

1 模型的假設

（1）假設每一個源點的發車數量都是最大值。（2）假設駕駛員駕駛的車輛滿足跟馳模型，即速度u與車輛密度k成線性關系。（3）假設在一個車道內無其他車輛超車或并排行駛。（4）假設每個車道只有一輛車行駛，不存在車輛并道，而且不允許超車。

2 名詞解釋及符號說明

Tij表示車輛從第i段路行駛到第j段路所用的時間；Sij表示車輛從第i點行駛到第j點的距離；L表示服務水平標準；A表示優性服務指數；T1表示正常行車時間；T2表示交叉路口延誤時間；fij表示每條道路上的汽車流量；Zij表示修正數據時道路上汽車“自由流”時間。

3 模型的建立與求解

3.1 問題一

（1）模型分析。該問題構建了一個道路圖系統，通過構建交通流均衡模型和時間優化模型對此問題進行求解。該文以最短時間作為目標函數，并且采用BPR路阻函數來表示總時間參數。

BPR時間路阻函數為：

其中，η表示人干擾的修正系數，η1表示自行車干擾的修正系數，δ，r 表示常量一般取δ=0.15，r =4，ηi 表示第η條通行道路的車流量，ci 表示第i條通行道路的設計車流量。可以得到以下表達式：

根據設置路網的參數可以將上述表達式化簡為：

其中，，S 表示道路長度，v 表示道路限速。同時，在該文所構建的道路網系統中，每一個節點處的汽車流入流量都等于流出流量，所以可以得到如下約束條件：

（2）模型的建立。根據以上分析，為了使得汽車行駛的總時間最短，得到其優化模型如下：

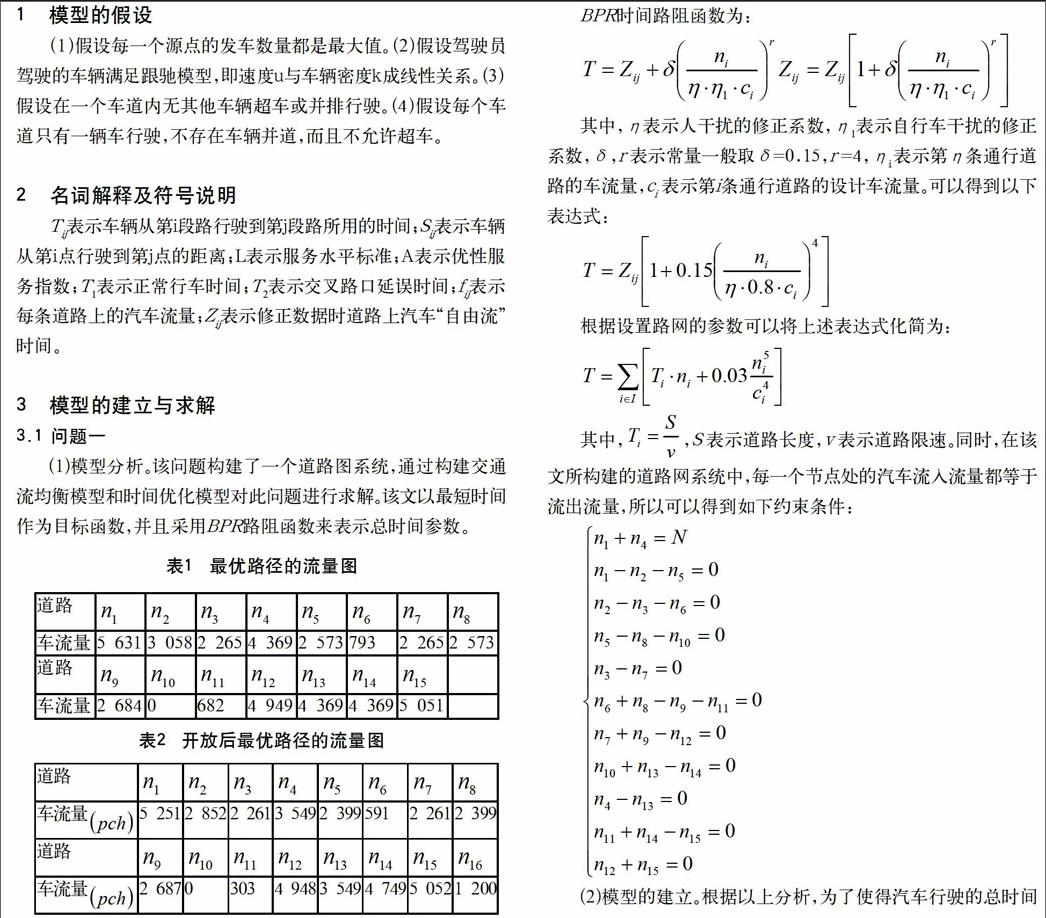
（3）模型的求解。根據所設置的路網系統，以下指標為系統有關的已知參數值（包括：時段、道路等級、限制車速、路程、基本通行能力） 使用軟件求解優化模型，當道路系統中所有車輛所花時間最少時，各條道路的流量見表1。

當小區在區域1時，開放小區道路后，最優路徑的車流量見表2。

3.2 問題二

在問題一的基礎上，該部分增加了對小區類型和周邊道路結構的考慮，以汽車出行時間以及交叉路口延誤時間為評價指標，定量比較各類型小區開放前后對道路的通行影響。

3.2.1 模型的建立

（1）交叉路口延誤時間。計算交叉口平均延誤時間時，該文采用Webster公式進行計算，其中t 表示信號燈時間周期長度，λ表示綠燈時間長度占總時間長度的比例，q表示進口道實際到達的交通流量，表示飽和度即，延誤的時間計算方法為：

最后可以得到，其交叉路口的平均延誤時間是一個關于車流量的函數。

（2）出行時間。在計算正常行車時間時，根據BPR路阻函數進行求解。在不考慮行人和非機動車影響的情況下利用未改進的BPR路阻函數[1]：

其中，表示從i 地到j 地自由流時的行走時間，表示從i 地到j 地的流量，表示從地到地的延誤參數[2]：

一般情況下將δ，r 取經驗值δ=0.15，r =4。

在小區內新建道路時，都會同時受非機動車和人員活動的干擾。考慮到非機動車和人員活動的影響，取人員干擾素為，非機動車干擾素為，當非機動車交通流量沒有超過通行能力的時候取。改進之后的BPR路阻函數為：

3.2.2 模型結論

根據以上模型的公式，利用程序和SPSS的處理求解可以得出：當遠離主干道住宅小區交通開放時，各路段所消費的時間與之前交通未開放時相比有明顯減少，道路上行車時間、延誤時間有一定程度緩解。當靠近主干道住宅小區交通開放時，各路段所消費的時間與之前交通未開放時相比有明顯減少，道路上行車時間、延誤時間有一定程度緩解。當遠離主干道商業小區交通開放時，各路段所消費的時間與之前交通未開放時相比有明顯減少，道路上行車時間、延誤時間有一定緩解。當靠近主干道商業小區交通開放時，各路段所消費的時間與之前交通未開放時相比有明顯減少，道路上行車時間、延誤時間有一定緩解。

從以上結論可以看出，不論是在哪的什么類型小區，只要進行小區開放，就會緩解路網的交通壓力，使道路上的行車時間、延誤時間有一定程度的降低。所以大部分指標在未開放和開放的差距不大，也就是說小區開放對緩解交通壓力的作用還是有一定限度的，而少部分路段的指標增減幅度是顯而易見的。

參考文獻

[1] 丁金學，鄭長江.路阻函數理論及其在路徑選擇中的應用[EB/OL].南京：中國科技論文在線，2007-11-26.

[2] 李向鵬.城市交通擁堵對策——封閉型小區交通開放研究[D].長沙：長沙理工大學，2015：1-5.