體育科研中檢驗統計量的角色及構造研究
孫永梅
(安徽師范大學 體育學院,安徽蕪湖 241000)
關于檢驗統計量,在確定總體、原假設與備擇假設的提前下,根據研究的需要與給定的已知數據信息,針對實際問題構造合適的檢驗統計量,不恰當的檢驗統計量影響統計結果,導致錯誤結論的出現。假設檢驗中各種方法的不同就體現在檢驗統計量的不同,不同的檢驗統計量由自身的硬性條繭浸俞合研究問題的需要所決定的。假設檢驗的具體方法中,檢驗統計量形式多樣。對于問題需要研究者認真思考,結合具體問題選用檢驗統計量來表達出有效的數據信息,而不是不假思索地用假設檢驗例行的程序分析所有問題。應用者往往把握不住其實質,遇到實際問題時往往不知使用哪種方法。筆者認為,檢驗統計量是根據實際問題的具體情況構造出來的,而不是符合什么條件就對應著什么檢驗統計量,不能顛倒其中的順序,不能生搬硬套。
綜上所述,要從根本上提高體育統計的應用水平,應用者需要掌握“構造檢驗統計量”的基本思想和方法。
1 檢驗統計量的角色剖析
檢驗統計量是用于檢驗原假設是否成立的統計量,它是用來判斷是否可以拒絕原假設的工具。檢驗統計量的信息來自于樣本信息的反饋,檢驗統計量的值是通過計算樣本數據得到的,并根據得到的數據對原假設和備擇假設做出判斷。
檢驗統計量在假設檢驗中扮演著重要角色。首先,檢驗統計量是樣本信息的集中載體,與課題研究有關的重要樣本信息都集中在檢驗統計量之中,因為統計量本身就是對樣本信息的加工;其次,檢驗統計量蘊含著原假設的信息,檢驗統計量的概率分布就是以原假設為前提的,可以說,原假設在假設檢驗的作用也是通過檢驗統計量來實現的,沒有檢驗統計量,原假設就將是孤立的,沒有任何意義。從假設檢驗的基本過程可以看出檢驗統計量的地位,假設檢驗的直觀思想:如果原假設成立,那么檢驗統計量應該服從某種概率分布,因而落在拒絕域的概率很小,如果檢驗統計量的值落在拒絕域,則拒絕原假設。可見,檢驗統計量在假設檢驗中的作用是舉足輕重的。
值得注意的是,檢驗統計量與檢驗統計量的值是不同的,檢驗統計量基于隨機樣本,是隨機變量,其概率分布取決于原假設,而檢驗統計量的值是基于樣本觀測值的,是一個具體的數。
2 檢驗統計量的構造
在假設檢驗中,通過總體將實際問題轉化為統計問題,采用相應的檢驗方法。根據研究需要選擇適當的檢驗方法,這里檢驗方法的選擇也就是檢驗統計量的構造問題,檢驗統計量的構造是進行假設檢驗的關鍵,也是檢驗結果正確與否的關鍵。
有些初學者常認為檢驗統計量只是公式而已,只要符合某個檢驗統計量的條件,即可直接帶入使用。然而公式并非只是公式,公式只是檢驗統計量的一種表現形式,檢驗統計量本身蘊含著統計思想。構造檢驗統計量既是統計應用的重點,又是難點。筆者認為,構造檢驗統計量需要考慮兩大要素:檢驗統計量的針對性和檢驗統計量的概率分布。
2.1 檢驗統計量的針對性
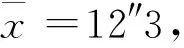
2.1.1 統計距離

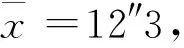
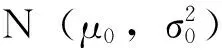
在參數檢驗中,關于總體均值的檢驗、總體率的檢驗,其統計量的構造原理是一樣的。只是根據分布的不同,而有所差異,其實質是提出問題,建立原假設,根據原假設,利用統計距離的想法,構造檢驗統計量。在多元統計分析中,檢驗統計量的構造也是利用統計距離的想法構造檢驗統計量的。在此,不再贅述。
2.1.2 比值
再現原假設,另一手段就是利用比值,檢驗統計量的構造與前面有所不同。
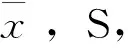
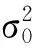
2.2 檢驗統計量的概率分布要明確
針對原假設,構造出來的統計量,能否作為檢驗統計量,一個至關重要的條件是該統計量的概率分布必須明確。如果統計量的分布不明確,即使該統計量具有針對性,也不能作為檢驗統計量。
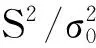
3 結束語
假設檢驗是統計分析的一種重要的方法,理解假設檢驗的思想是實際應用的根本前提。在體育科研中,應用者需要掌握假設檢驗的思想,結合體育學科自身的特點,方能科學、靈活地運用假設檢驗方法。構造檢驗統計量的實質是度量樣本信息與原假設的“出入”程度,因此,檢驗統計量的構造既要依據原假設,又要保證檢驗統計量的概率分布明確。
參考文獻:
[1] 劉欽龍.體育科研中提高統計處理效果的若干要素[D].蕪湖:安徽師范大學,2003:8—37.
[2] 李時.應用統計學[M].北京:清華大學出版社,2005:68—80.
[3] 理查德·A. 約翰遜,迪安·W,威克思.實用多元統計分析[M].北京:清華大學出版社,2008:161—198.
[4] 賈俊平,何曉群,金勇進.統計學[M]. 陸璇, 葉俊,譯.北京:中國人民大學出版社,2008:209—241.

