半導體材料的微重力生長

尹志崗，張興旺，吳金良

(1.中國科學院半導體研究所 半導體材料科學重點實驗室，北京 100083)(2.中國科學院大學材料科學與光電技術學院，北京 100049)

?

半導體材料的微重力生長

尹志崗1,2，張興旺1,2，吳金良1

(1.中國科學院半導體研究所 半導體材料科學重點實驗室，北京 100083)(2.中國科學院大學材料科學與光電技術學院，北京 100049)

空間微重力環境提供了一個獨特平臺，以改進地面材料性能、深入理解被地面重力掩蓋的晶體生長現象。半導體空間材料科學的主要進展有：①基于對組分均勻的完美半導體的追求，人們對于晶體生長機理，特別是對流、溶質傳輸及組分分凝的相互作用，有了更加深入的理解；②基于空間實驗結果，人們澄清了非接觸 Bridgman生長的內在機理，并將之用于指導空間及地面實驗；③提出了新的微重力晶體生長技術并成功用于組分均勻半導體合金材料的制備。回顧了以上方面的研究進展，并對半導體空間材料科學的未來挑戰進行了展望。

微重力；浮力對流；Marangoni對流；Bridgman生長；非接觸生長

1 前 言

空間技術的進步為材料科學的發展帶來了新的機遇。20世紀60年代末開始的空間材料生長實驗宣告了一門新學科——微重力材料科學的誕生。空間微重力環境為材料的生長、加工提供了新的自由度，同時有力地促進了人們對材料生長基礎問題的認識。微重力材料科學的研究目標主要包括3個方面：通過抑制重力效應，制備地面無法得到的高性能材料；理解被地面重力效應掩蓋的物理現象；改進地面晶體生長工藝[1]。

半導體是信息社會的材料基礎，也是空間材料科學最為重要的研究方向之一[2]。空間半導體材料生長實驗多采用以浮區法、Bridgman法為代表的熔體生長技術[3-5]。特別是Bridgman法，由于其簡單易行的優點，是半導體空間材料科學實驗的主流方法。本文將主要圍繞Bridgman法展開，同時適當兼顧目前有潛力的新生長技術。總的來講，半導體空間材料科學領域取得的主要進展概括為如下3方面：

(1)基于抑制浮力對流、實現純擴散生長的目標，科學家開展了多種半導體體系的空間生長實驗。通過這些工作，人們對于各種對流現象與溶質輸運、組分分凝之間的相互作用有了更加深入的理解，這些認識反過來又極大地促進了晶體生長學科的發展。

(2)通過微重力實驗發現了非接觸Bridgman生長這一現象，并認識到其對于降低缺陷、提升晶體質量的巨大意義。基于空地實驗結果，人們澄清了非接觸Bridgman生長的基本原理，并成功將之用于指導空間及地基晶體生長過程[6]。

(3)以移動加熱器法、移動液相區法及垂直梯度凝固法為代表的新的微重力晶體生長技術不斷涌現，并成功制備了各種高質量的半導體合金晶體。

本論文將立足于以上3個方面，介紹空間半導體材料科學近年來的發展概況。

2 通向純擴散生長

2.1 微重力條件下的組分偏析與溶質輸運

根據經典的Tiller理論，當對流可以忽略而溶質輸運過程由擴散控制時，可以實現穩態生長，即固體組分為恒定值[7,8]。擴散機制控制溶質輸運時，固體中的溶質濃度分布符合以下關系(見式(1))[8]：

Cs(x)/C0=k+(1-k)[1-exp(-kRx/D)]

(1)

其中Cs(x)為距離初始位置x處固體中的溶質濃度，C0起始狀態下熔體的平均溶質濃度,k為平衡分配系數,D溶質在熔體中的擴散系數,R為生長速度。根據式(1)，穩態生長時(x足夠大)固體組分Cs(x)與C0一致。通常為表述實際情況與這一理想情況偏離的程度，定義有效分凝系數(見式(2))[8]：

keff=Cs/C0

(2)

當keff不為1時，說明實際晶體生長過程偏離了純擴散生長(熔體中溶質輸運只受擴散規律支配)，即產生了組分偏析。但是，由于浮力對流的影響，在地面環境下很難實現純擴散生長。利用微重力環境，抑制浮力對流、制備組分均勻的完美晶體，是人們開展空間材料科學實驗的重要原因之一。

Witt等人基于InSb開展的微重力材料生長實驗表明，沿晶體軸向的雜質分布均一，符合純擴散生長的特征。類似的結果后來也多有報道[9-12]。但在空間生長的Ge晶體中，雜質分布盡管在軸向是均勻的，但在徑向卻與期望結果有很大差距[10]。同樣，在GaAs及HgCdTe空間晶體中也觀察到了同樣的現象[11,12]，其中HgCdTe晶體的徑向組分分布如圖1所示。這些結果揭示，空間晶體生長并不能簡單歸結為純擴散過程，實際情況要復雜得多。在實際的空間飛行器中，重力水平雖較地面大幅降低，但卻遠不是零。殘余重力(準靜態加速度和動態加速度)的存在對于晶體生長過程有不可忽視的影響。穩態生長需要在生長界面附近(邊界區)的熔體中建立穩定的溶質濃度分布，任何對于這一平衡狀態的破壞，包括殘余重力引起的對流，都有可能導致組分偏析的出現。例如，Alexander 等[13]記錄了動態加速度的實時變化，首次發現了動態加速度與溶質輸運間的緊密聯系。不難理解，隨重力水平減小，沿軸向組分會逐漸逼近keff，組分最終會穩定在C0。徑向組分分凝的特點與軸向有顯著差別，它隨重力水平及對流強度的變化并不是單調的。在無對流(無重力)及強對流(地面)兩種極限條件下，晶體組分沿徑向均分布均勻。殘余重力引起的弱環形對流不僅決定了熔體邊界區的局域溶質分布，還會使徑向各點傳熱條件產生差異，因此會導致晶體徑向組分分布的明顯變化[14]。相對而言，殘余重力對軸向組分分布的影響并不顯著。這就導致了空間材料科學實驗中經常觀察到的現象——軸向組分均勻，徑向偏析嚴重。

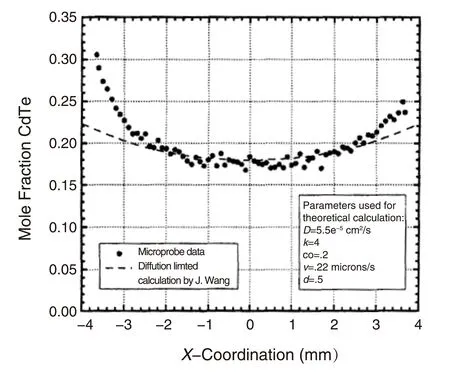
圖1 HgCdTe徑向組分分布圖；圖中虛線為根據擴散生長機制計算所得[12]Fig.1 Radial composition profile of HgCdTe crystal. The dashed line indicates the calculated results according to the diffusion-controlled scheme[12]

人們開展了大量的計算模擬工作，旨在深入理解殘余重力對溶質輸運及分凝過程的影響。Naumann[15]建立了二維流場的解析模型，發現10-4g0(g0為地面重力加速度)的殘余重力就足以導致熔體中溶質分布的劇烈變化，同時指出生長爐軸線與殘余重力矢量方向平行時可在一定程度上抑制這種影響。Alexander等[16]也得到了類似的結論。此外，他們的研究還揭示，動態加速度本身雖是一種瞬時作用，對溶質輸運過程的影響卻可持續～1000 s之久。Derby小組[17]近來發展了Bridgman生長的三維模型，將熔體對流、熱傳導、分凝及凝固等過程悉數納入，成功用來模擬、指導CdZnTe晶體的生長。Stelian等[18]給出了液-固界面演化的半經驗表達式，得到了平直界面所需的動力學條件。該小組還仔細審視了動態加速度的頻率、幅度對于組分分凝的影響(如圖2)，結果顯示：頻率恒定時，動態加速度幅度越大，偏析越嚴重；幅度恒定時，相對于高頻加速度，低頻加速度的影響更加致命[19]。理論模擬盡管不能完全再現空間生長過程，卻是理解微重力環境下對流、溶質輸運及組分分凝相互作用不可或缺的工具，對于具體的空間實驗設計也有著重要的指導意義。

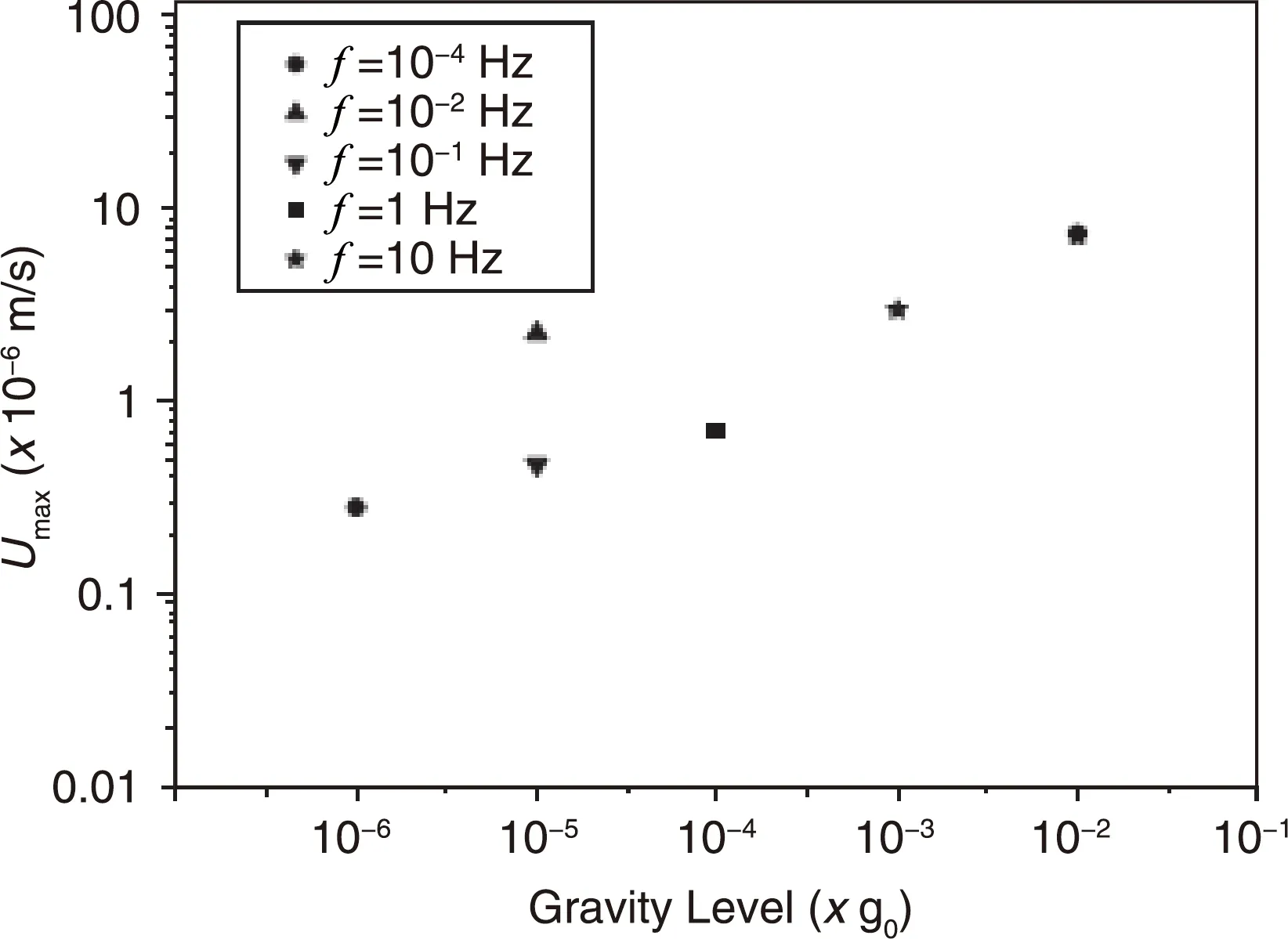
圖2 殘余重力對熔體對流的影響，其中Umax對應最大對流速度[19]Fig.2 Effect of the residual gravity on the melt convection, in which Umax is the maximum convective velocity[19]

2.2 Marangoni對流的影響

浮力對流的驅動力可以用Rayleigh數來表示(見式(3))：

Ra=gβΔTL3/αγ

(3)

式中g為重力加速度，β為熱膨脹系數，ΔT為溫度梯度，L為熔池深度，α為熱擴散系數，γ為動力黏度。式(3)顯示，Rayleigh數與重力加速度成正比。可以預期，在微重力環境下浮力對流強度將大為降低。但是，Te摻雜GaSb空間晶體中觀察到了明顯的軸向組分分凝，這一結果顯然不能由殘余重力引起的浮力對流來解釋[20]。理論與實驗結果均指向Marangoni對流，一種在地面環境下經常被重力效應所掩蓋的現象。理論模擬證實，在浮力對流得到抑制且存在自由表面的情況下，對流強度可以完全由Marangoni對流主導[14]。實際測量顯示，在1.2 K/cm的徑向溫度梯度下，固-液界面附近的對流速度可高達0.5 cm/s，幾乎與地面條件下浮力對流引起的效應相當[14]。可以說，在許多微重力材料科學實驗中，Marangoni對流都與樣品在徑向及軸向的宏觀偏析現象密切相關。

Marangoni對流不僅會可造成宏觀偏析，還可導致微觀偏析的產生。在實驗上，微觀偏析主要表現為生長條紋，其形成主要與晶體生長過程中的溫度起伏或生長速率起伏引起溶質濃度漲落造成的。一言以蔽之，微觀偏析與失穩對流相關，而與穩態對流無關。生長條紋還是一種研究晶體生長機理的有力工具，可以用來表征生長界面的動力學演變過程[21]。在微重力環境下，Rayleigh數遠小于穩態-失穩轉變臨界值，因此浮力對流一般不是生長條紋出現的主要原因。例如，在封閉表面的條件下，即使在動態加速度強度高達2×10-1g0，Ge∶Ga晶體生長過程中也未出現可分辨的生長條紋[14]。通常來講，空間生長的晶體樣品中若出現生長條紋，Marangoni對流是必須要考慮的因素。Marangoni對流的驅動力由Marangoni數來表示(見式(4)和式(5))：

MaT=αSTLΔT/αγ

(4)

MaC=αSCLΔω/Dγ

(5)

MaT和MaC分別為溫度驅動和組分驅動Marangoni對流對應的Marangoni數，αST和αSC分別為表面張力的溫度系數和溶質濃度系數，Δω為溶質濃度差。在溫度漲落幅度為0.5～0.7 ℃，頻率小于0.5 Hz時，Schweizer等[22]發現Si的生長速度在1 mm/min的平均速度左右出現了明顯的起伏。觀察到的生長速度最高為4 mm/min，最小甚至可為負值(晶體回熔)，因此晶體中出現了明顯的生長條紋(如圖3)。這是Marangoni對流造成微觀偏析的典型例子。若Marangoni對流是微觀偏析的主導因素，Marangoni數必須大于Ma2(Ma2為穩定-失穩Marangoni對流轉變臨界值)。確定Ma2的大小，是微重力Marangoni對流研究的重要內容，眾多小組就此問題展開了研究。Cr?ll等[23]仔細測量了GaSb的臨界Marangoni數，得到的Ma2值為375±125，與理論計算結果(355±90)非常吻合。對于Si和GaAs，實驗得到的Marangoni數分別為150±50 和～400[23]。基于這些結果，可以外推得到Ma2與Prandtl數(Pr，流體動力黏度與熱擴散系數的比值)的對應關系為(見式(6))[23]：

Ma2=2.2×104Pr1.32

(6)

這一關系式對于預測其它體系的微觀偏析行為具有重要指導意義。

由式(4)和(5)可知，Marangoni對流的驅動力與溫度梯度或濃度梯度線性相關。因此，降低溫度梯度或濃度梯度，是控制Marangoni對流的有效手段。但是，對于 Bridgman技術來說，溫度梯度是爐體的固有屬性，固-液界面附近熔體中的溶質濃度梯度又是擴散生長的必然結果，因此實際上這兩種方法并不可行。本課題組注意到中科院物理所、中國空間技術研究院蘭州物理所以及日本東京大學利用我國返回式衛星搭載的GaSb空間實驗晶體盡管出現了自由表面，卻未觀察到可分辨的生長條紋[24-26]。作者認為，未出現失穩Marangoni對流的原因與GaSb表面薄的氧化物保護層有關。Tillberg等[27]基于Ge晶體的空間生長實驗結果，也強調了表面氧化層對于生長條紋的抑制作用。在不致引起晶體摻雜污染的前提下，引入惰性氧化層無疑是抑制自由表面形成，進而調控Marangoni對流的可行手段。

圖3 微重力生長的Si單晶腐蝕照片，圖中由Marangoni對流引起的生長條紋清晰可見[22]Fig.3 Image of the etched μg0 crystal of Si, in which dopant striations induced by Marangoni convection are clearly visible[22]

2.3 抑制對流的途徑

如前所述，空間材料科學實驗的目的之一是利用微重力環境抑制對流，實現純擴散生長，以便得到組分均勻分布的摻雜半導體或半導體合金。但是，由于殘余重力的存在及自由表面的出現，浮力對流及Marangoni對流的影響仍舊不可忽視，通向組分均勻分布的完美半導體之路并不平坦。很顯然，對于空間材料科學來說，如何進一步抑制對流是一個極其重要的課題。

很久之前，靜磁場就被認為是與微重力類似的抑制對流的手段。例如，Cr?ll小組[28]詳細研究了磁場對于Si晶體生長過程的影響，發現施加磁場可以完全避免生長條紋的出現。但是，后續研究結果顯示，若通過靜磁場在地面環境下抑制對流，進而實現由擴散主導的溶質輸運過程，磁場強度至少需要達到若干個特斯拉[29]。強磁場會帶來2個弊端：①經濟上代價太大；②會引起熱電磁對流等副效應[29]；因此在技術上并不現實。隨著研究的深入，微重力與弱磁場相結合作為一個可行的研究路徑受到關注，許多小組在這方面進行了卓有成效的嘗試。例如，Fripp等[30]試圖利用軸向磁場抑制徑向對流分量，并基于垂直Bridgman方法進行了數值模擬。結果顯示，在微重力條件下，只需數千高斯的磁場就足以有效抑制浮力對流效應。Baumgartl 等[31]的結果也證實，磁場的強度及取向對于其實際使用效果有顯著的影響。Herrmann等[32]在微重力環境下進行了GaAs晶體的生長，但由于施加磁場強度過小，效果并不特別明顯。從技術上而言，在空間飛行器上施加數千高斯的磁場稍顯奢侈。改靜磁場為旋轉磁場，或許是解決問題的可行辦法。與靜磁場不同，旋轉磁場的作用是產生強制對流，以補償熔體中已有的對流效應。在俄羅斯Foton-M3衛星上開展的Ge∶Ga晶體生長實驗中，旋轉磁場的施加使得生長條紋明顯變弱[33]。Dold及合作者也在Ge∶Ga體系中發現了類似的結果[34]。

Lan等[35,36]通過系列模擬工作，研究了通過坩堝旋轉技術抑制動態加速度效應、控制組分偏析的可行性。他們發現，微重力環境下不高于20 r/min的旋轉速度即可產生與地面100 r/min相同的效果。計算結果進一步顯示，在采用坩堝旋轉技術時，晶體軸向組分分布可接近純擴散生長極限，而徑向偏析也能得到顯著改善。除此之外，該小組還考慮了偏心旋轉的可能影響，發現只要偏心角不過大，對晶體組分分布的影響基本可以忽略不計。

從式(3)中可以看出，Rayleigh數與L3及成正比，可以利用這一特點來設計實驗方案以抑制浮力對流。例如，將熔池深度降低一個量級，浮力對流水平將相應地下降3個量級。此外，減小爐體溫場梯度，也能在一定程度上抑制浮力對流強度。Ostrogorsky[37-39]設計了下沉加熱器這一新穎的加熱模式，大幅降低了有效熔池深度，并減小了爐體溫場梯度，在地面條件下實現了Ge基和InSb基晶體的準擴散生長。隨后，進一步簡化方案，利用高熱傳導材料石墨制備的下沉隔板替代下沉加熱器，也能起到類似的效果[40]。利用這一技術，科學家在國際空間站開展了Te摻雜InSb及Zn摻雜InSb的生長工作，并取得了預料中的效果[41,42]。由于Marangoni數與L線性相關，可以預期，下沉隔板法對于Marangoni對流不會特別有效。除了2.2節介紹的表面氧化層，更有效的抑制Marangoni對流的方法其實是設法消除自由表面。相關內容會在3.3節略作討論。

3 非接觸 Bridgman生長

3.1 非接觸Bridgman生長的發現及其意義

1970年代Witt等[9]利用Bridgman法進行InSb空間生長時，意外發現晶體外徑竟然明顯小于坩堝的內徑。這顯然不是由熱脹冷縮所致，因為InSb在液-固轉變時通常會產生體積膨脹。這種現象被稱為非接觸生長(Detached Growth)，其示意圖如圖4所示[43]。從概念上講，非接觸生長指的是晶體本身與器壁不接觸，而熔體絕大部分與器壁是接觸的。從純幾何的角度而言，非接觸生長需滿足熔體浸潤角與晶體生長角之和大于180°的條件[43]。一般的半導體材料與坩堝組合，很難滿足這一苛刻的條件。除InSb外，其它半導體，如 Ge、GaSb、CdTe等，也都在微重力環境下觀察到了非接觸生長現象[24,44]。盡管微重力環境并不總是導致非接觸生長，但非接觸生長確實可以稱得上是空間半導體Bridgman生長的典型特征之一。但在地面環境下，基于同樣的實驗條件、同樣的裝置，地面條件下卻總是難以觀察到非接觸生長。很顯然，非接觸出現與否與重力場有密切的關系。與空間情形相比，地面環境下熔體自身具有靜壓力，這可能是導致空間與地面實驗產生差異的原因。但是，其背后具體的機理，在很長時間內都不是很清楚。

圖4 布里奇曼法溫場分布曲線(a)，正常布里奇曼生長示意圖(b)，非接觸布里奇曼生長示意圖(c)，微重力環境下制備的Ge晶體照片(從中可以很清楚看到非接觸生長)(d)，地面重力環境下生長的Ge晶體照片(e) [43]Fig.4 Temperature profile needed for Bridgman growth (a), schematic of Bridgman growth (b), schematic of detached Bridgman growth (in which α stands for the growth angle and θ is the contact angle of the melt) (c), Ge crystals grown by Bridgman method under microgravity (d) and on the ground (e) [43]

在常規Bridgman生長時晶體與坩堝壁是接觸的，由于晶體與坩堝材料熱膨脹系數的差異，晶體與坩堝壁之間會產生顯著的熱失配。例如，常用的石英坩堝熱膨脹系數約為5×10-7/K，要比多數半導體的熱膨脹系數小一個量級。晶體與坩堝間的熱失配會造成晶體中缺陷(特別是位錯)密度的顯著增加，使得晶體質量大幅降低。熱失配嚴重時，甚至會導致微裂紋等宏觀缺陷的形成。實驗結果顯示，非接觸生長由于避免了晶體與坩堝壁之間的直接接觸，因此可以有效降低熱失配，進而使晶體中位錯密度大大降低。根據Dold等[43]及Schweizer等[45]的報道，非接觸生長可使Ge晶體位錯密度下降約2個數量級。在空間生長的CdZnTe晶體中，也觀察到了類似的現象[46]。最驚人的結果來自InSb體系[44]，空間非接觸生長的晶體位錯密度僅僅為2.5×10 /cm2，而地面常規樣品的位錯密度則高達104～105/cm2！低的位錯密度對于研制高性能器件的意義不言而喻。例如，陳諾夫等[3,47]基于低位錯密度的空間半絕緣GaAs單晶制造的低噪聲場效應晶體管和模擬開關集成電路，其各項性能均超過了地面材料制造的相同器件。

3.2 非接觸生長機理

自20世紀90年代以來，通過Duffar等[48,49]的一系列理論及實驗工作，非接觸生長的原因才算徹底搞清楚。非接觸生長時晶體與器壁之間存在間隙，三相交界線與器壁之間依靠彎液面來連接。典型的Bridman非接觸生長時彎液面及晶體-器壁間隙附近的示意圖如圖5所示，在晶體-器壁間隙處(熔體下端)及熔體上端存在氣體(揮發所致)。根據拉氏方程，在彎液面兩側的壓力差為(見式(7))[49]：

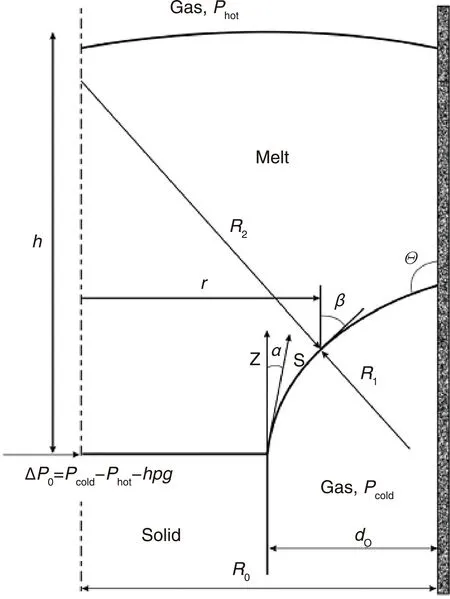
圖5 非接觸生長彎液面區域示意圖。Pcold與Phot：熔體下端及上端的氣相壓力；h：熔體區高度；R0：坩堝的半徑；R1：彎液面曲率半徑；R2：彎液面曲率半徑(垂直于紙面方向)[48,49]Fig.5 Schematic of the meniscus region in the detached growth. Pcold and Phot are gas pressures below and above the melt, h is the height of the melt, R0 the radius of the crucible, and R1 and R2 are the meniscus radii (R1 in the plane of the figure, R2 in the plane perpendicular to R1)[48,49]

ΔP=σ=(1/R1+1/R2)

(7)

其中σ為表面張力。由圖5可知(見式(8)和式(9))[49]：

R1=-ds/dβ

(8)

R2=r/cosβ

(9)

在彎液面附近，ΔP可表示為坐標z的方程(見式(10))[49]：

ΔP=ΔP0+zρg

(10)

其中ΔP0為三相點處的壓力差，ρ為熔體密度，g為重力加速度。綜合(7)～(10)式，有(見式(11))[49]：

dβ/ds-cosβ/γ=-ΔP/σ=-(Pcold-Phot)+ρg(h-z)/σ

(11)

很明顯，(11)式左端與彎液面的形狀有關，右端第一項反映了熔體上、下端氣相壓力對彎液面形狀的影響，第二項則代表了重力的貢獻。利用(11)式，可以通過數值解析的方式對晶體生長的形態進行預測。Kaiser等[50]對Ge晶體的Bridgman生長進行了數值模擬，其中晶體生長角α選為11°，表面張力σ取為0.5969 N/m，結果如圖6所示。可以看到，α+θ< 180°時，晶體-坩堝間隙在ΔP≈ -200 Pa時取最大值。晶體-坩堝間隙當ΔP<-200 Pa時急劇減小，在ΔP> -200 Pa時則緩慢地以對數關系衰減。根據Lyapunov穩定性條件[48]，晶體-熔體界面處的彎液面必需向氣相一側凸出，在動力學上才能夠穩定存在。根據計算，ΔP> -10 Pa時彎液面為凹進型，所以不利于晶體-坩堝間隙的穩定存在[49]。綜合考慮以上因素，α+θ< 180°條件下穩定的非接觸生長需要ΔP位于-200 ～ -100 Pa的區間。α+θ> 180°時，彎液面形狀在ΔP< 0 Pa時始終滿足Lyapunov動力學穩定條件，理論上在該壓力區間均可實現非接觸生長[49]。但是，由于ΔP< -2000 Pa時晶體-坩堝間隙過小，與坩堝表面粗糙度在一個數量級，此時并不能出現非接觸生長。因此，α+θ> 180°條件下出現非接觸生長的ΔP范圍在-2000～0 Pa區間。

在重力環境下，熔體靜壓力對于ΔP有重要貢獻。半導體熔體密度通常在5 g/cm3左右，假設熔體區高度為10 cm，則熔體靜壓的貢獻約為-5000 Pa。由此可見，對于α+θ< 180°和α+θ> 180°兩種情況，ΔP取值都遠遠偏離了非接觸生長的條件。這樣，在地面實驗中很少能夠觀察到非接觸生長，也就不難理解了。另外，從圖6a和6b中還可以看出，接觸角越大，越有利于實現非接觸生長。鑒于非接觸生長在降低位錯等缺陷密度方面的巨大優勢，人們期望在地面環境下也能夠實現非接觸生長。

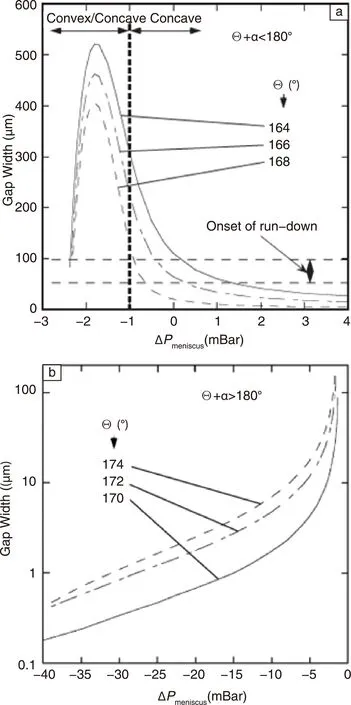
圖6 間隙寬度與彎液面兩側壓差的關系：(a) θ+α< 180°,(b) θ+α> 180°[48]Fig.6 Gap width as a function of pressure differential across the meniscus for θ+α< 180° (a) and θ+α> 180° (b) [48]

3.3 非接觸生長機理指導地面及空間實驗

根據上述討論，使熔體下端相對于熔體上端過壓，是實現地面非接觸生長的前提條件。根據具體情況，實現熔體下端過壓的途徑各有不同。具體而言，實現熔體下端過壓的方法主要有3種：①通過外部氣源實現過壓；②通過溫度梯度變化誘導過壓產生；③在熔體下端引入易揮發原料。第3種方法只對CdTe、GaAs等含有高飽和蒸汽壓組元的材料有效，適用范圍較為受限。前兩種方法具有通用性，適用于所有的半導體材料。第一種方法的核心在于兩端開口的安瓿結構，其熔體上端及下端分別通過開口與外部氣源相連接，因而這兩部分的氣體壓力可以由外部氣源獨立控制[48]。通過該方法，很容易使熔體下端的過壓抵消熔體靜壓力的貢獻，使得體系滿足非接觸生長的壓力條件。隨著生長的進行，熔體上下端空間此消彼長，因而兩端的壓差始終處于動態變化中，顯然不利于得到恒定的晶體直徑。為解決這一問題，Yeckel等[51]最近發展了線性及非線性的比例-積分反饋控制技術，這一局限性有望得到解決。

第二種方法的核心思想最早由Szofran等[43]提出。在這一方法中，密封的安瓿中預先充入惰性氣體，之后加熱使原料區處于熔融狀態。在生長開始時，降低熔體上端處的溫度，這樣就可人為制造出熔體上下端的壓差。當然，為實現這一目的，爐體必需具備多段爐絲加熱、各段可單獨控溫的能力。隨著生長的持續進行，熔區-溫場對應關系會逐漸改變，進而破壞非接觸生長所需的條件。因此，安瓿上端的溫度應隨著生長的進行，不斷做出相應的調整。Duffar等[52]在研究GaSb體系的非接觸生長時，提出了一種改進的方案——在籽晶下端引入特殊設計的“氣體庫”，“氣體庫”氣壓可根據需要由溫度來調控。由于“氣體庫”與晶體區的溫度控制是獨立進行的，這一方案可有效實現熔體下端過壓，且不影響晶體生長所需的最佳溫場曲線設置。基于溫度梯度變化誘導過壓的方法，人們實現了Ge晶體的非接觸Bridgman生長，得到的位錯密度約為2×102/cm2，比常規接觸生長得到的晶體降低了1到2個量級[45]。需要說明，非接觸生長本身并不罕見，常規的浮區法就可以做到。但是，非接觸Bridgman生長卻可以有效克服浮區法晶體直徑有限的缺憾，在制備低缺陷濃度半導體晶體方面仍具有巨大的吸引力。基于對非接觸生長機理的深刻理解，在地面環境下借助于非接觸Bridgman技術實現高質量半導體晶體的生長，是空間材料科學最為引人矚目的成就之一。

半導體熔體是一種具有低Prandtl 數的流體，表現為高的熱導率和低的粘滯性。因此，在地面環境下一般很難獲得穩定的自然對流。通過解析的方法，很難對隨機、失穩的流形進行嚴格求解，這既影響對于晶體生長過程的深入理解，也不利于導出精確的晶體生長參數。微重力條件盡管不能完全抑制自然對流，但多數情況下可以獲得穩定的對流狀態，為解決上述問題創造了難得的條件。但是，在自由表面出現的情況下，Marangoni對流這一地面次級效應的作用會凸顯出來，使得問題復雜化。對于Bridgman方法來說，基于對自由表面(非接觸生長)出現原因的透徹理解，可以通過一定的手段有效消除Marangoni對流的影響。Ostrogorsky等[41,42]在國際空間站開展了Te摻雜InSb及Zn摻雜InSb晶體的批量生長工作。在該實驗中，安瓿中采用了改進的活塞及彈簧機構，使得安瓿內壓力條件避開了非接觸生長區，因而抑制了自由表面的形成，最大限度降低了Marangoni對流的影響。為了實時觀察固-液界面的具體形態，判斷自由表面有無形成，生長爐配備了原位觀察系統。該小組利用Tiller理論，由純擴散生長起始瞬態的理論表達式擬合了所得的軸向組分分布曲線(如圖7)。結果顯示，摻雜組分分布與純擴散生長的理論預期基本一致。同時，還得到了擴散系數這一晶體生長參量的可信數值。

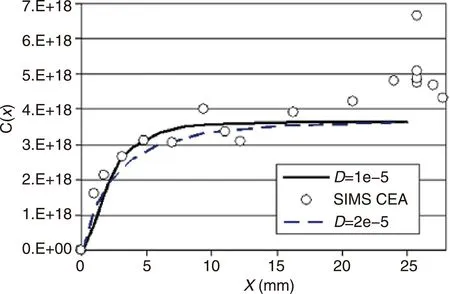
圖7 Te摻雜InSb雜質分凝曲線(其中實線及虛線分別表示在擴散系數為1×10-5 cm2/s 和2×10-5 cm2/s情況下的有限元計算結果)[41]Fig.7 Dopant segregation profile of the Te-doped InSb (the solid and dashed lines are based on finite element calculations using diffusion coefficients of 1×10-5 cm2/s and 2×10-5 cm2/s)[41]

4 空間晶體生長新方法

4.1 移動加熱器法

除了Bridgman方法外，其它的晶體生長方法，如移動加熱器法(Traveling Heater Method, THM)，近年來也得到了越來越多的關注。THM又稱為移動溶劑區法，顧名思義，是一種采用局部區域熔融生長晶體的方法。但與Bridgman方法不同，THM本質上是一種助熔劑法，通過助熔劑的添加來降低生長結晶溫度。HTM法示意圖如圖8所示[53]，在籽晶和原料區之間夾有低熔點助熔劑，隨著生長界面不斷前移，助熔劑被不斷排向未熔融的原料區，通過這個過程可實現晶體的連續結晶生長。在HTM方法中，原料區界面溫度要始終高于結晶界面，否則難以保持原料的持續熔化和晶體的連續生長。HTM法在近些年已成為空間半導體生長的主流技術手段之一，特別是在CdTe及CdZnTe研究方面，HTM法似乎有著不可替代的地位[54]。理論模擬揭示，通過在微重力環境下抑制對流，可以獲得更加穩定的HTM生長界面和更加均勻的組分分布。Borisenko等[55]在俄羅斯Foton-M4衛星上進行的實驗表明，微重力確實有助于獲取組分均勻的CdZnTe晶體。相對于地面樣品，空間CdZnTe樣品具有更完美的晶體質量((220)峰搖擺曲線半高寬僅為39.5 arc sec)、更少的富Te沉淀顆粒(數量下降4倍)、更好的半絕緣性(電阻率～109Ω cm)，為高效離子輻射探測器的制備奠定了基礎。實驗還發現，施加低頻弱旋轉磁場，有利于減少富Te沉淀相、提高CdZnTe的組分

均勻性及電學均一性[56]。理論研究肯定了低頻小磁場在促進生長界面穩定性、提高CdZnTe空間晶體質量方面的有益作用，但也強調，磁場是一把雙刃劍，在磁場強度較大時其副作用通常更加突出[57,58]。總的來講，HTM法的優點是晶體生長可以在遠低于熔點的溫度下進行，在生長具有大偏析效應、高蒸汽壓的材料時優勢明顯；缺點在于溶質濃度低，晶體生長速度偏慢。例如，對于CdZnTe，其生長依賴于通過熔化界面溶解的Cd、Zn向結晶界面的遠距離連續傳輸，生長速度僅為3～5 mm/d。生長速度慢，無疑大大影響了HTM法的實用性。

圖8 THM方法原理示意圖[53]Fig.8 Schematic illustration of the THM method[53]

4.2 移動液相區法

移動液相區法(Traveling Liquidus-Zone Method，TLZ)是一種與HTM法類似的晶體生長技術，亦采用三明治(籽晶區-低熔點區-原料區)樣品安瓿結構，其中籽晶區與原料區為同一種材料(如圖9)[59,60]。TLZ法本質上是一種熔體法，這是與作為溶液法的HTM的主要區別。因為這一特征，TLZ法在生長時液相區溶質濃度相對更大，因此理論上具有更快的生長速度。加溫時，低熔點區融化，高熔點的籽晶區及供料區不斷溶解進入液相區，形成合金熔體；籽晶-熔體界面處溶質飽和時，合金晶體生長便自然發生。此時界面處的質量平衡方程為(見式(12))[60]：

(12)

其中CL和CS分別代表固-液界面兩側液相和固相中的溶質濃度，R為自發生長速度，D為擴散系數。假設CL只與溫度相關，即CL=CL(T)，則式(12)右側可寫作：

(13)

于是，式(12)變為：

(14)

其中?T/?x為固-液界面處的溫度梯度，?CL/?T則依賴于溶質分布，一般情況下較為復雜。當忽略對流的影響，溶質傳輸過程僅由擴散決定時，界面處CL在給定溫度下可認為取飽和值，即與液相線對應的溶質濃度一致。若固-液界面位置固定，式(14)右側在給定的溫度下將為定值。為確保固-液界面位置恒定，通常液相區以速度R向晶體生長的反方向移動。由上面的討論可知，在溶質輸運由擴散主導時，移動液相區法可以得到組分均勻分布的晶體。假如CL>CS，則當移動速度大于R時，晶體中溶質濃度在軸向逐漸變小；而當移動速度小于R時，晶體中溶質濃度的變化趨勢相反。特別強調，在重力場下，只有在體系徑向尺寸很小(可視為準一維系統)時，對流的影響才可近似忽略。當體系徑向尺寸較大時，由于對流的影響，界面附近溶液很容易出現過飽和或欠飽和，上面討論的情況不再成立。因此，移動液相區法在地面原則上只能制備直徑很小的組分均勻晶體。根據Kinoshita等[59]的報道，TLZ法可成功生長直徑為1.5～2 mm的In0.3Ga0.7As單晶，但當直徑增加時，晶體質量及組分均勻性急劇變差。理論模擬表明[60]，在晶體徑向尺寸增加時，如果籽晶采用熱傳導性更好的材料，同時降低坩堝的熱傳導系數，組分分布的均勻性可以得到改善，這點今后的工作或許可以加以嘗試。

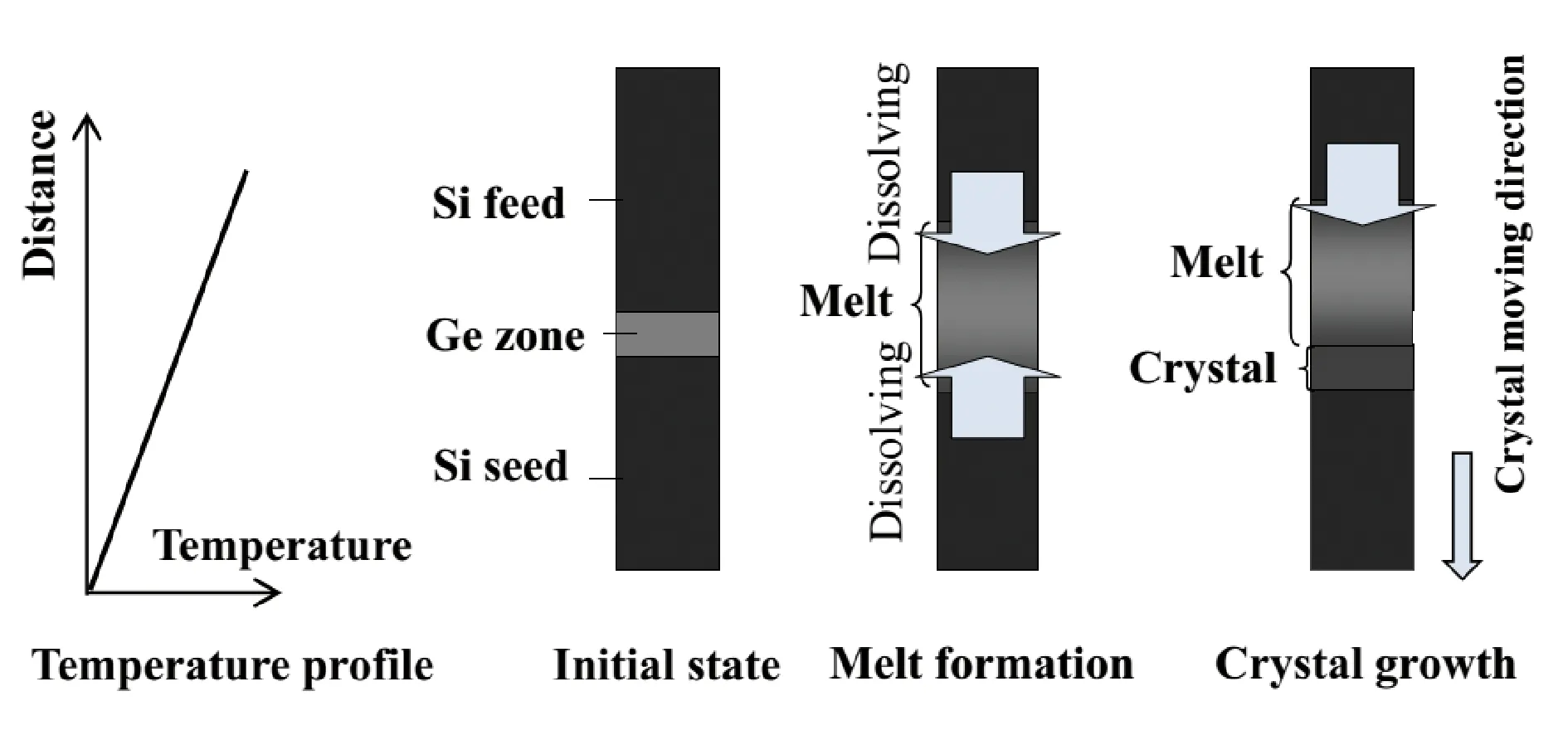
圖9 TLZ法生長晶體示意圖(以SiGe體系為例說明)[59,60]Fig.9 Schematic of the TLZ method (taking the SiGe system as an example)[59,60]

日本JAXA研究團隊利用國際空間站實驗平臺開展了Si0.5Ge0.5晶體的TLZ生長工作[61]，晶體生長爐的溫度梯度為9 ℃/cm，晶體直徑約10 mm，晶體提拉速度為0.1 mm/h，總的生長時間為117 h。得到的Si0.5Ge0.5晶體外形如圖10a所示，對應的Ge組分二維分布見圖10b。由于籽晶外徑略小于BN坩堝內徑，在生長時籽晶-坩堝間縫隙內會有熔體滲入，滲入的熔體使得籽晶/晶體界面在接近晶體外緣處向籽晶一端凸進。除晶體外緣區之外，其它區域的籽晶/晶體界面尖銳平直。總體而言，在所生長的區域內(> 10 mm)內，無論徑向還是軸向，Ge組分分布都非常均勻。圖10c和10d進一步給出了樣品Ge組分在軸向及徑向的分布情況，可以看出，組分波動在軸向小于2%，而在徑向則不大于1%。可以看出，TLZ法在微重力條件下制備組分均勻的半導體合金，具有其它技術難以比擬的優勢。最近，Kinoshita等[62]發現，相對于小的溫度梯度，大的溫度梯度更易導致多晶的出現。除溫度梯度外，同一小組[63]還對生長速度等其它生長參數對Si0.5Ge0.5生長過程的影響進行了詳細研究。

圖10 SiGe樣品實物圖 (a)，組分二維分布圖(b)，軸向組分分布(c)，徑向組分分布(d) [61]Fig.10 Outer view of the SiGe crystal (a), 2D Ge concentration map (b), axial concentration profiles (c) and radial concentration profile (d) [61]

4.3 垂直梯度凝固法

垂直梯度凝固法(Vertical Gradient Freezing Method, VGF)與TLZ方法原理類似[64]，均采用了三明治構型，不同之處在于采用VGF方法生長晶體時，晶體相對加熱區并不移動，而代之以固定溫度梯度下的緩慢降溫。如果降溫速度選取合適，使得固-液界面的溫度恒定，原則上也可以生長出組分均勻的多元半導體(假設液相始終飽和)。本質上，VGF其實與TLZ是同一種方法。VGF不需要任何機械傳動機構，只需要精確的一維溫場控制即可實現晶體生長。在微重力環境下，任何的機械運動都可能帶來g-顫動的問題，所以VGF在用于空間晶體生長實驗時，潛在的優勢非常突出。VGF目前主要應用于InxGa1-xSb晶體的微重力生長，典型的實驗結果如圖11所示[64]。所用的 GaSb、InSb晶錠為(111)取向，直徑為10 mm，皆由切氏法提拉而成。GaSb-InSb-GaSb三明治結構密封于BN坩堝之中，樣品區兩端由石墨片固定。與地面樣品相比，空間樣品Ga組分空間分布明顯更均勻。另外，在地面由于強對流的存在，晶體籽晶/晶體界面極不規則，而空間晶體的界面就更加規則平直。為得到InGaSb的實際生長速度并研究生長過程中界面的動態演變過程，Inatomi等[21]采用了施加周期性加熱脈沖的方法，人為引入生長條紋，通過生長條紋的分布來間接推理上述信息。通過空地對比研究，他們得到如下結論：①在地面環境下，InGaSb的生長自籽晶邊緣開始，而空間晶體則沿籽晶徑向幾乎同時開始；②通過測量生長條紋間距，推測微重力條件下晶體生長速度略大于地面；③微重力條件下穩態生長階段持續的距離比地面要大得多。同一小組[65]還研究了不同籽晶終止面的結晶生長規律，發現由于GaSb(111)B更易溶解，當采用GaSb(111)B為籽晶時，InGaSb生長速度較使用GaSb(111)A籽晶更快。

5 結 語

微重力半導體材料科學實驗始于對完美晶體的追求。盡管美夢未能成真，微重力這一獨特平臺仍然從理論及實驗兩方面極大地促進了半導體晶體生長技術的發展。利用微重力環境，人們將Marangoni對流從浮力對流的影響中分離出來，獨立予以研究，對于晶體生長相關的質量輸運過程有了深入的理解。對溶質傳輸與各種對流形式之間相互作用的深刻認識反過來又促進了晶體生長技術的發展，人們開發了多種有效的對流控制技術，在地面環境已經實現了準擴散生長。基于微重力環境，人們發現了以非接觸 Bridgman生長為典型的一系列新的晶體生長現象，而對于這些現象的深入思考又帶來了地基晶體生長技術的巨大進步。最近，以移動液相區法為代表的半導體合金生長技術取得了突破，所得空間晶體無論在軸向還是徑向，都無明顯偏析產生。盡管這些技術目前所生長的材料種類仍非常有限，但從原理上看，其可推廣性是確定無疑的。

圖11 空間樣品(a)及地面樣品(b)的外觀圖、熔區示意圖及Ga組分二維分布圖[64]Fig.11 Outside views, schematic representation of the dissolved area, and Ga composition profile around the center of the space-grown crystal (a), earth-grown crystal (b) [64]

經過多年的發展與積累，今后微重力半導體材料科學的發展脈絡已經隱約可見：①不以完美晶體為目標，著重于利用微重力這一特殊的工具，探索晶體生長的新現象，挖掘其背后的新機理；②重視硬件研發，多段加熱、溫場精確可控、配備有各種原位監控檢測裝置的生長爐是今后空間材料科學實驗的必然要求；③學科交叉愈來愈重要，微重力晶體生長方面的進步離不開材料科學與流體物理的密切合作；④對于最近發展起來的半導體合金生長技術(如移動液相區法)進行進一步的微重力實驗驗證，并將之拓展至更多的材料體系。

References

[1] Benz K W, Dold P.JCrystGrowth[J], 2002, 237: 1638-1645.

[2] Chen Wanchun(陳萬春)，Song Youting(宋友庭).SciTechnolRev(科技導報)[J], 2012, 30: 46-57.

[3] Chen N F, Zhong X R, Lin L Y,etal.ApplPhysLett[J], 2001, 78: 478-479.

[4] Wang Z G, Li C J, Cao F N,etal.JApplPhys[J], 1990, 67: 1521-1524.

[5] Lin L Y, Zhong X R, Chen N F.JCrystGrowth[J], 1998, 191: 586-588.

[6] Ebnalwaled A A, Duffar T, Sylla L.CrystResTechnol[J], 2013, 48: 236-244.

[7] Tiller W A, Jackson K A, Rutter J W,etal.ActaMet[J], 1953, 1: 428-437.

[8] Smith V G, Tiller W A, Rutter J W.CanJPhys[J], 1955, 33: 723-745.

[9] Witt A F, Gatos H C, Lichtensteiger M,etal.JElectrochemSoc[J], 1975, 122: 276-283.

[10]Witt A F, Gatos H C, Lichtensteiger M,etal.JElectrochemSoc[J], 1978, 125: 1832-1840.

[11]Bly J M, Kaforey M L, Matthiesen D H,etal.JCrystGrowth[J], 1997, 174: 220-225.

[12]Gillies D C, Lehoczky S L, Szofran F R,etal.JCrystGrowth[J], 1997, 174: 101-107.

[13]Alexander J I D, Garandet J P, Favier J J,etal.JCrystGrowth[J], 1997, 178: 657-661.

[14]Strelov V I, Kuranova I P, Zakharov B G,etal.CrystallogrRep[J], 2014, 59: 781-806.

[15]Naumann R J.JCrystGrowth[J], 1994, 142: 253-267.

[16]Alexander J I D, Ouazzani J, Rosenberger F.JCrystGrowth[J], 1989, 97: 285-302.

[17]Derby J J, Kwon Y, Pandy A,etal.AnnNYAcadSci[J], 2006, 1077:124-145.

[18]Stelian C, Duffar T.JCrystGrowth[J], 2005, 275: e585-e594.

[19]Stelian C, Duffar T.JCrystGrowth[J], 2005, 275: 175-184.

[20]Duffar T, Serrano M D, Lerin L,etal.CrystResTechnol[J], 1999, 34: 457-465.

[21]Inatomi Y, Sakata K, Arivanandhan M,etal.NPJMicrogravity[J], 2015, 1: 15011.

[22]Schweizer M, Cr?ll A, Dold P,etal.JCrystGrowth[J], 1999, 203: 500-510.

[23]Cr?ll A, Kaiser T, Schweizer M,etal.JCrystGrowth[J], 1998, 191: 365-376.

[24]Nishinaga T, Ge P, Huo C,etal.JCrystGrowth[J], 1997, 174: 96-100.

[25]Nakamura T, Nishinaga T, Ge P,etal.JCrystGrowth[J], 2000, 211: 441-445.

[26]Voloshin A E, Lomov A A, Nishinaga T,etal.JCrystGrowth[J], 2002, 236: 501-510.

[27]Tillberg E, Carlberg T.JCrystGrowth[J], 1990, 99: 1265-1272.

[28]Cr?ll A, Szofran F R, Dold P,etal.JCrystGrowth[J], 1998, 183: 545-553.

[29]Yesilyurt S, Vujisic L, Motakef S,etal.JCrystGrowth[J], 1999, 207: 278-291.

[30]Yao M W, Chait A, Fripp A L,etal.JCrystGrowth[J], 1997,173: 467-480.

[31]Baumgartl J, Müller G.JCrystGrowth[J], 1996, 169: 582-586.

[32]Herrmann F, Müller G.JCrystGrowth[J], 1995, 156: 350-360.

[33]Barmin I V, Senchenkov A S, Greif A,etal.Magnetohydrodynamics[J], 2009, 45: 325-331.

[34]Dold P, Benz K W.CrystResTechnol[J], 1997, 32:51-60.

[35]Lan C W, Tu C Y.JCrystGrowth[J], 2002, 237: 1881-1885.

[36]Lan C W.JCrystGrowth[J], 1999, 197: 983-991.

[37]Ostrogorsky A G.JCrystGrowth[J], 1990, 104: 233-238.

[38]Ostrogorsky A G, Sell H J, Scharl S,etal.JCrystGrowth[J], 1993, 128: 201-206.

[39]Dutta P S, Ostrogorsky A G.JCrystGrowth[J], 1999, 197: 749-754.

[40]Dutta P S, Ostrogorsky A G.JCrystGrowth[J], 2000, 217: 360-365.

[41]Ostrogorsky A G, Marin C, Churilov A,etal.JCrystGrowth[J], 2008, 310: 364-371.

[42]Ostrogorsky A G, Marin C, Volz M P,etal.JCrystGrowth[J], 2009, 311: 3243-3248.

[43]Cr?ll A, Volz M P.MRSBull[J], 2009, 34: 245-250.

[44]Regel L L, Wilcox W R.MicrogravitySciTechnol[J], 1998, XI/4: 152-166.

[45]Schweizer M, Cobb S D, Volz M P,etal.JCrystGrowth[J], 2002, 235: 161-166.

[46]Sylla L, Fauler A, Fiederle M,etal.IEEETNuclSci[J], 2009, 56: 1747-1751.

[47]Lin Lanying(林蘭英)，Zhang Mian(張 綿)，Zhong Xingru(鐘興儒)，etal.SciChinaE[J], 1999, 42: 456-461.

[48]Duffar T, Dusserre P, Picca F,etal.JCrystGrowth[J], 2000, 211: 434-440.

[49]Palosz W, Volz M P, Cobb S.JCrystGrowth[J], 2005, 277: 124-132.

[50]Kaiser N, Cr?ll A, Szofran F R,etal.JCrystGrowth[J], 2001, 231: 448-457.

[51]Yeckel A, Daoutidis P, Derby J J.JCrystGrowth[J], 2012, 356: 33-45.

[52]Duffar T, Dusserre P, Giacometti N.JCrystGrowth[J], 2001, 223: 69-72.

[53]Peterson J H, Fiederle M, Derby J J.JCrystGrowth[J], 2016, 454: 45-58.

[54]Stelian C, Duffar T.JCrystGrowth[J], 2014, 400: 67-75.

[55]Borisenko E B, Kolesenikov N N, Senchenkov A S,etal.JCrystGrowth[J], 2017, 457: 262-264.

[56]Salk M, Fiederle M, Benz K W,etal.JCrystGrowth[J], 1994, 138: 161-167.

[57]Stelian C, Duffar T.JCrystGrowth[J], 2015, 429: 19-26.

[58]Li Z Y, Peterson J H, Yeckel A,etal.JCrystGrowth[J], 2016, 452: 17-21.

[59]Kinoshita K, Kato H, Iwai M,etal.JCrystGrowth[J], 2001, 225: 59-66.

[60]Adachi S, Kinoshita K, Takayanagi M,etal.JCrystGrowth[J], 2011, 334: 67-71.

[61]Kinoshita K, Arai Y, Inatomi Y,etal.JCrystGrowth[J], 2015, 419: 47-51.

[62]Kinoshita K, Arai Y, Inatomi Y,etal.JCrystGrowth[J], 2016, 455: 49-54.

[63]Kinoshita K, Arai Y, Inatomi Y,etal.IntJMicrogravitySciAppl[J], 2016, 33: 330213.

[64]Yu J, Liu Y, Pan X H,etal.MicrogravitySciTechnol[J], 2016, 28:143-154.

[65]Kumar V N, Arivanandhan M, Rajesh G,etal.NPJMicrogravity[J], 2016, 2: 16026.

(編輯 吳 琛)

Microgravity Growth of Semiconductor Materials

YIN Zhigang1,2, ZHANG Xingwang1,2, WU Jinliang1

(1.Key Lab of Semiconductor Materials Science, Institute of Semiconductors, Chinese Academy of Sciences, Beijing 100083, China)(2.College of Materials Science and Opto-Electronic Technology, University of Chinese Academy of Sciences, Beijing 100049, China)

The microgravity environment aboard the space provides a unique platform to synthesize materials with improved properties as compared with their terrestrial counterparts, and allows an in-depth understanding of crystal-growth-related phenomena that are masked by gravity on the earth. The main achievements in the microgravity growth of semiconductors are listed below: ①the seeking of perfect crystals with chemical homogeneity benefits a profound understanding on the crystal growth process, typically on the relationships among the convective flows, solute transport and chemical segregation; ②based on the microgravity experiments, the underlying mechanism of detached Bridgman growth was clarified and used to guide the space- and ground-based crystal growth processes;③new crystal growth schemes were proposed and implemented successfully to grow chemically homogeneous semiconductor alloys under microgravity. In this review, the main progresses in these aspects are summarized and the future challenges are discussed.

microgravity; buoyancy-driven convection; Marangoni convection; Bridgman growth; detached growth

2017-03-25

中國載人空間站工程(TGJZ800-2-RW024)；中國科學院戰略性先導科技專項項目(XDA04020202-11, XDA04020411)

尹志崗，男，1976年生，副研究員，碩士生導師

張興旺，男，1972年生，研究員，博士生導師， Email:xwzhang@semi.ac.cn

10.7502/j.issn.1674-3962.2017.04.01

O782

A

1674-3962(2017)04-0241-11