基于M—C與D—P屈服準則及局部強度折減法的邊坡穩定性分析

廖敏

摘要： 邊坡失穩主要是由于局部土體強度降低所造成的，采用傳統整體強度折減法對邊坡土體所有單元進行折減分析與工程實際不相符合。本文基于Mohr-Coulomb（M-C）和Drucker-Prager（D-P）屈服準則，運用局部強度折減法和傳統整體強度折減法對邊坡穩定性進行對比分析。結果表明M-C模型與D-P線性模型計算結果最為相近和合理，相差不大；局部強度折減法所得安全系數、位移量相比整體強度折減法要偏小，更具有合理性。

Abstract： Slope instability is due to the decrease of local soil's strength. It is not accordance with the engineering practice， using the traditional overall strength subtraction method to analyze all the elements of soil slope. This paper is based on Mohr-Coulomb （M-C） and Drucker Prager （D- P） yield criterion， using local strength subtraction method and traditional overall strength subtraction method analysed and compared slope stability. Results show that the results of M-C model and D-P linear model calculation are reasonable and most closely， the difference are small； compared with overall strength subtraction method， the safety factor、displacement of local strength subtraction method are smaller， it is more reasonable.

關鍵詞： 局部強度折減；邊坡；安全系數；穩定性分析

Key words： local strength reduction；slope；safety factor；stability analysis

中圖分類號：U418.5+2 文獻標識碼：A 文章編號：1006-4311（2017）13-0082-03

0 引言

有限元整體強度折減法對邊坡的穩定性分析時，對土體內所有單元進行強度折減，但是在實際工程中邊坡失穩主要是由于局部土體的強度降低所致，而其余部位巖體力學參數影響很小。若對所有土體單元進行強度折減，對邊坡進行穩定性評價并不準確[1-2]，所求解出來的結果并不能很好地反映出邊坡失穩時的真實情況，故而用局部強度折減法能夠更加真實滿足工程需要，對邊坡的穩定性分析具有重要意義。

ABAQUS軟件對經典的D-P模型進行了擴展，屈服面在子午面的形狀可以通過線性函數、雙曲線函數和指數函數模擬，在一定條件下D-P與M-C模型可以實現參數相互轉換。國內學者運用擴展的D-P模型與M-C模型對邊坡穩定性問題開展了較多的研究工作：易紹基等[3]利用M-C模型和D-P指數模型對邊坡土性參數進行研究，認為塑性參數對邊坡安全系數影響最大；張芳枝等[4]利用D-P雙曲線模型對某堤防進行了穩定分析，認為應將張拉-剪切復合屈服準則應用到邊坡分析；伍韻瑩等[5]利用D-P線性模型對邊坡進行模擬認為宜聯合采用位移判據和塑性區判據對邊坡的穩定性進行分析；陳浩等[6]利用D-P線性模型通過Python語言對某地下洞室群分期開挖動態模擬。以上大都是利用整體強度折減法對土體所有單元進行折減，與實際工程有所偏差，而且現有研究將ABAQUS里面的M-C模型和D-P模型結合局部強度折減法對邊坡進行分析研究還比較少。故而本文用有限元軟件ABAQUS通過整體強度折減法和局部強度折減法，結合M-C準則和D-P準則對邊坡進行分析計算。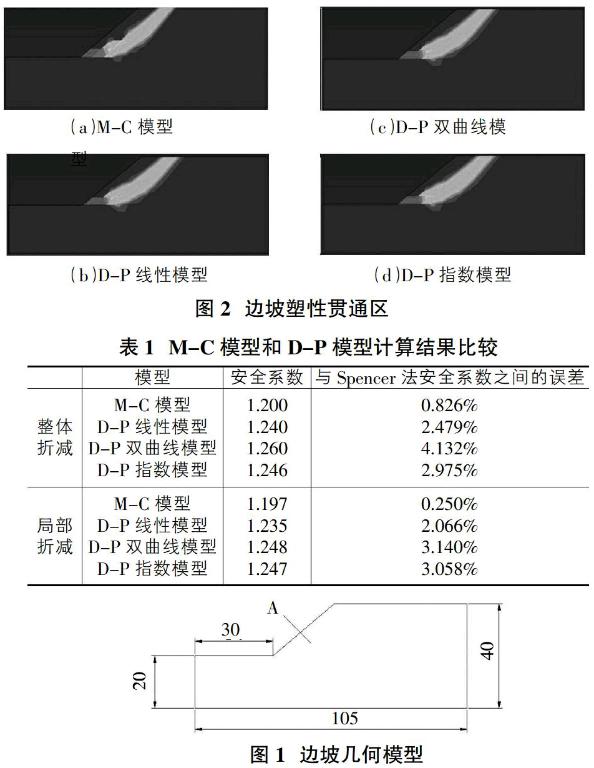

1 強度折減法與模型參數轉換

1.1 局部強度折減法原理

邊坡失穩是土體抗剪強度失效，剪切應變增量引起土體單元進入屈服階段，形成塑性屈服階段的單元區域，即塑性貫通區，也就是潛在滑裂帶。局部強度折減法與傳統的有限元強度折減法不同，它是指通過不斷降低局部土體的強度，致使邊坡達到臨界失穩狀態的方法。可以根據勘察報告判斷邊坡的潛在滑裂帶或軟弱土層作為局部土體，若缺乏相關資料，可以先對整個土體單元強度折減，可以得到塑性貫通區的土體單元作為滑裂帶土體，然后只對塑性區土體單元的抗剪強度參數進行折減[7]。折減后的抗剪強度參數可以分別表達為：

邊坡破壞的判斷依據主要有三個準則：一是以數值計算不收斂作為土坡穩定的評價標準；二是以特征點的位移拐點來作為評價標準；三是以結構面塑性區貫通作為評價標準。第一種依據由于收斂準則的不同會導致安全系數的差異；趙尚毅等[8]認為塑性區從坡腳到坡頂貫通并不一定意味著邊坡破壞，塑性區貫通只是破壞的必要條件，但不是充分條件；第二種依據有著明確的理論意義，因此本文采用位移突變作為判斷依據來評判邊坡穩定性。

1.2 M-C與D-P模型的參數轉換

基于平面應變的前提下，M-C模型與D-P模型的參數轉換，費康[9]等作了相關的研究并給出了轉化公式，故不贅述，只簡單羅列公式。在用分析同一邊坡時，需要對M-C模型與D-P模型參數進行轉換。當D-P線性模型的三軸拉伸強度等于三軸壓縮強度，二者的屈服面非常接近，M-C模型參數與D-P線性模型參數可以相互轉換，D-P線性模型轉化公式為：

2 邊坡分析計算

2.1 土坡的穩定性分析

本文選取鄭穎人等[11]和張魯渝等[12]做的一個土坡作為計算實例來驗證對比整體強度折減法和局部強度折減法在M-C模型與D-P模型中的應用情況。土坡高H=20m，土體容重為25kN/m3，彈性模量為1000kPa，泊松比為0.3，粘聚力為42kPa，內摩擦角為17，坡腳取為40°。由于鄭穎人等[11]所得的安全系數與Spencer極限平衡法的結果最為接近，故而本文用Spencer極限平衡法的計算結果來作比較，其安全系數為1.21。由于分析中考慮了剪脹角會使安全系數偏高，而傳統極限平衡方法沒有考慮剪脹角的影響使結果較為保守。為了與傳統極限平衡法的結論相一致，方便對比，分析中不考慮剪張角的影響[13]。本例取在邊坡節點A（網格劃分后的節點，A點在塑區內）處的位移拐點作為判斷依據，計算模型如圖1所示。

要用局部強度折減對邊坡進行分析，需要得到邊坡的潛在滑裂帶。可以先利用軟件對邊坡所有土體單元進行強度折減，然后將所得到的塑性變形貫通區作為邊坡的滑裂帶。如圖2所示，依次為M-C模型、D-P線性模型、D-P雙曲線模型、D-P指數模型的塑性貫通區變形云圖。

然后提取圖2中塑性貫通區的單元節點，僅對以上的塑性貫通區域的土體進行強度折減，其他土體強度保持不變。選取安全系數、安全系數與Spencer法之間的誤差作為計算結果進行比較，如表1所示。

由表1可知，兩種強度折減計算的安全系數與Spencer極限平衡法計算得到的安全系數十分接近，誤差很小，計算結果是可靠的。局部強度折減與整體折減相比，安全系數略有降低，安全系數誤差變小。從局部折減的結果看：M-C模型和D-P線性模型的第安全系數與Spencer極限平衡法給的安全系數最為接近；D-P雙曲線模型和D-P指數模型的安全系數與Spencer極限平衡法誤差相對較大。

以上邊坡例子較為理想，但是在實際工程中修建了大量的工程設施，這些工程在建設中會形成大量的高、陡邊坡。故而需要驗證以上結果在實際工程中應用性，本文選取M-C模型和D-P線性模型對下文的巖質邊坡進行穩定性分析對比。

2.2 工程實例分析

選取閻寒等[14]做的一個人工巖質邊坡工程實例來進行穩定性分析。某巖質邊坡一級坡率1：1，坡高3m，第二、三級坡率1：0.5，每級坡高7m，具體模型如圖3所示。該巖質邊坡的巖性主要為強風化花崗巖和中等風化花崗巖，巖性參數如表2所示。分析過程中假設兩巖體界面連接良好，各個土體都是各向同性的均質材料。根據邊坡安全系數以特征點的位移突變性為失穩判據，閻寒等用FLAC3D軟件基于強度折減法算出的安全系數為2.2，邊坡處于穩定狀態。根據上文的結論，采用M-C模型和D-P線性模型對巖質邊坡進行穩定性分析。取在邊坡節點B（網格劃分后的節點，B點在塑性區內）處的位移拐點作為判斷依據，采用局部強度折減法對該邊坡進行分析。先對邊坡整體進行強度折減后得到塑性區滑裂帶，然后塑性區以外的土體強度保持不變，再對滑裂帶進行強度折減。

計算中采用非關聯流動法則，選用非對稱算法（Un-symmetric），采用M-C模型和D-P線性模型對所有土體進行折減后得到的塑性貫通區滑裂帶如圖4所示，然后提取塑性貫通區土體單元節點，對塑性區進行強度折減，計算結果如表3所示。

由表3可知局部折減后的安全系數相比整體折減小，兩種屈服準則所得的安全系數與FLAC3D軟件所算的結果很接近，且略小于FLAC3D軟件所得的安全系數，黃天成[15]認為如若以位移突變作為評判邊坡的穩定性，FLAC3D計算所得的安全系數大于ABAQUS。故而兩種屈服準則基于整體強度折減法和局部強度折減法分析邊坡的結果是合理的。

表3中局部強度折減的位移相比整體強度折減小，是因為僅對邊坡滑裂帶區域進行強度折減，減少了滑裂帶以外區域土體的因強度折減引起的位移增量，故而得出的位移比全局強度折減法要小，其符合邊坡的實際情況。從位移結果來看，D-P線性模型計算得到的最終位移略大于M-C模型，這是因為屈服準則的不同所致，但總體而言，M-C模型與D-P線性模型計算結果很相近。實際工程中，可以將M-C模型與D-P線性模型相結合來計算邊坡的穩定性。

本文采用M-C模型的整體折減和局部強度折減后的位移等值線云圖進行對比，如圖5所示。采用整體折減和局部折減對邊坡進行計算后的邊坡滑動面大致一樣，局部折減的位移略小于整體折減，兩則最大位移均發生在邊坡坡頂，且位移較小；二者的滑動面位置大致一樣，滑動面位置呈大致的圓弧狀，并且通過坡腳點，滑動土體主要是邊坡上半沿的強風化花崗巖和中風化花崗巖土體。由安全系數可知，邊坡由于邊坡處于穩定狀態。但如果遇到不當的人類工程活動、強降雨、雪等，容易對邊坡安全造成影響。

3 結論

采用ABAQUS軟件結合強度折減法對土坡和巖質邊坡進行了穩定性分析，得到了以下結論：

①采用局部強度折減法計算所得安全系數、位移量、比整體強度折減法小，與工程實際更為接近，用局部強度折減法來分析邊坡比整體強度折減法更為合理，驗證了局部折減法的可行性。②M-C模型和D-P線性模型計算結果很相近，建議可將M-C模型和D-P線性模型相結合利用局部強度折減法對邊坡進行計算。

參考文獻：

[1]趙川，付成華.基于局部強度折減法的某水電站邊坡穩定性分析[J].人民珠江，2015，36（3）：66-69.

[2]鐘志輝.邊坡分析的局部強度折減法及其工程應用[D].廣州：華南理工大學，2012.

[3]易紹基，黃英，韓玲，等.土性參數對邊坡穩定性的影響研究[J].水利與建筑工程學報，2011，9（3）：1-7.

[4]張芳枝，陳曉平，梁志松.強度折減有限元在堤防穩定分析中的應用研究[J].工程地質學報，2011，19（2）：244-249.

[5]伍韻瑩，王志鵬，孫立宇.Mohr-Coulomb內切圓屈服準則在ABAQUS軟件邊坡分析中的應用[J].長春工程學院學報（自然科學版），2012，13（2）：52-55.

[6]陳浩，肖明，衡為方.基于ABAQUS大型地下洞室群分期開挖動態模擬[J].武漢大學學報（工學版），2013，46（3）：321-327.

[7]楊光華，鐘志輝，張玉成，等.用局部強度折減法進行邊坡穩定性分析[J].巖土力學，2010，31（Z2）：53-58.

[8]趙尚毅，鄭穎人，張玉芳.極限分析有限元法講座—Ⅱ有限元強度折減法中邊坡失穩的判據探討[J].巖土力學，2005，26（2）：332-336.

[9]費康，張建偉.ABAQUS在巖土工程中的應用[M].北京：中國水利水電出版社，2010.

[10]易紹基.基于ABAQUS的邊坡穩定敏感性分析及模型驗證[D].昆明：昆明理工大學，2011.

[11]鄭穎人，趙尚毅，張魯渝.用有限元強度折減法進行邊坡穩定分析[J].中國工程科學，2002，4（10）：52-56，78.

[12]張魯渝，鄭穎人，趙尚毅，等.有限元強度折減系數法計算土坡穩定安全系數的精度研究[J].水利學報，2003，34（1）：21-27.

[13]高志輝.有限元邊坡穩定參數敏感性分析[D].北京：北京工業大學2007.

[14]閻寒，杜海濤，徐寶儒，等.基于強度折減法的人工巖質邊坡穩定性分析[J].電力勘測設計，2013，4（2）：12-16.

[15]黃天成.FLAC3D計算單滑面巖質邊坡影響因素討論[J].科技傳播，2013（8）：119-12.