短區間特征和的一些表達式

王念良

（商洛學院 數學與計算機應用學院/應用數學研究所，陜西商洛 726000）

1 引言與結論

定義1[1]設p是奇素數，n是正整數，(p,n)=1。若同余方程：

有解，則稱n是模p的二次剩余；若無解，則稱n是模p的二次非剩余。

二次剩余理論是初等數論中非常重要的結論與組成部分。17世紀到18世紀，費馬、歐拉、拉格朗日和勒讓德等數論學家對二次剩余問題作了初步研究，證明了部分定理并作出了一些相關的猜想，高斯是首先對二次剩余進行系統研究的數學家，他在著作《算術研究》中首次引入了術語“二次剩余”與“二次非剩余”的概念[1]。二次剩余不僅可用來判斷二次同余式是否有解，而且在實際中有廣泛的應用，如從噪音工程學到密碼學以及大數分解等[2-5]。

設χ是模q的Diriclet特征，令Gn(χ)=表示關于特征χ的廣義高斯和(χ)=表示關于特征χ的高斯和。關于特征 χ的 Dirichlet函數 L(s,χ)定義為[3]：

設 k,α 是非負整數，r是正整數,q=pα，χ是模p的Dirichlet本原特征。關于特征χ的短區間和定義[3-4]為：

定理設k,α 是非負整數，r是正整數,q=pα。當素數p≡1(mod 4)時，勒讓德符號

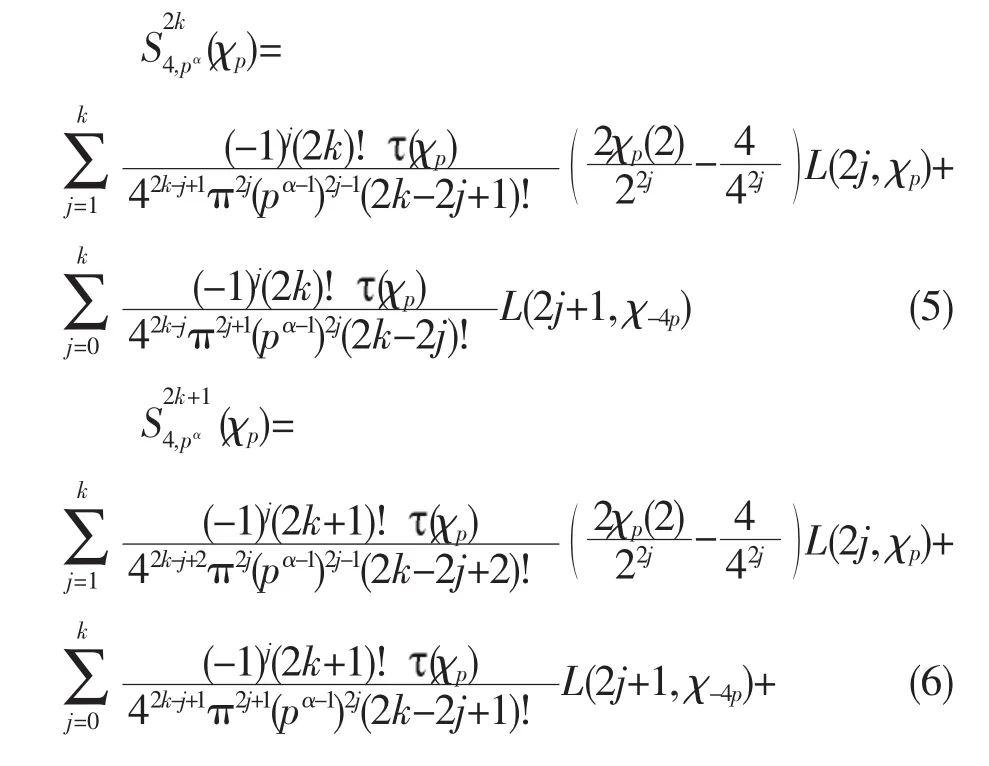
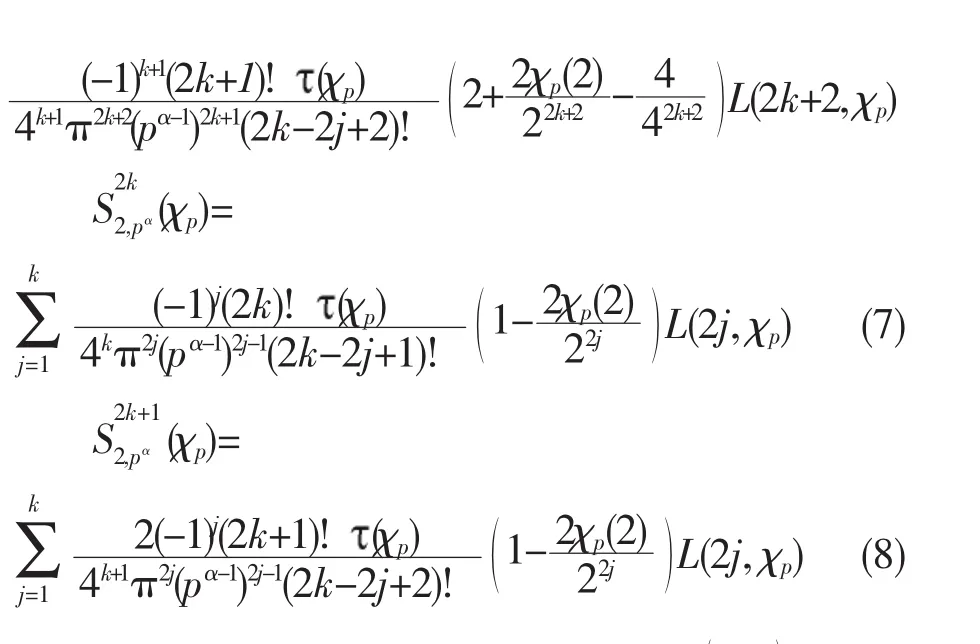
2 結論的證明

為了完成定理的證明，首先敘述一個引理。

引理 1[3]設 k,α,t,u 是非負整數，0＜t≤u，q=pα,χ是模p的Dirichlet本原特征，則

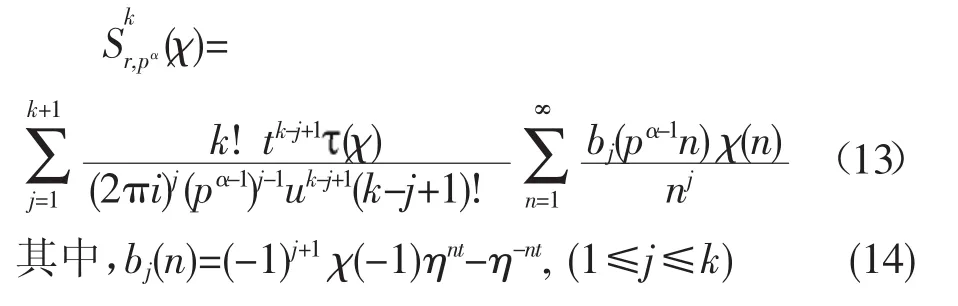
引理1的證明根據文獻[3]引理1,取即得，略。

定理的證明由于定理中8個公式的證明過程是類似的，僅對定理中(5)(7)(9)(11)給出詳細證明，其余的讀者可類似的給出證明過程。

在引理 1中，當p≡1(mod 4)時，注意到pα-1≡1(mod 4)，取，則 t=1,u=4 由(14)(15)式得：

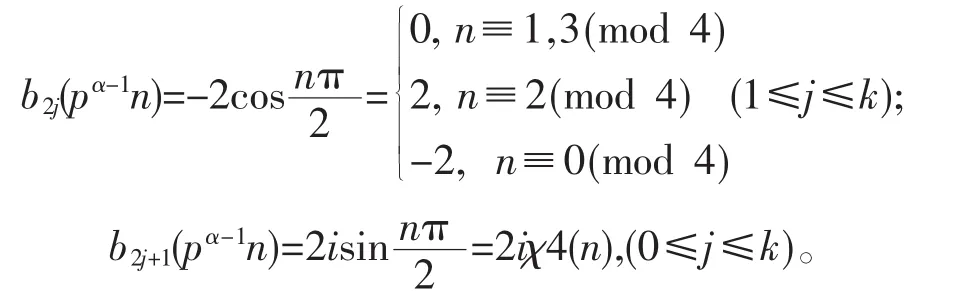
將(13)式右端和式按下標的奇偶性分成兩部分，注意到：

由(16)(17)式即有(5)式。類似的，可證明(6)式。

此時，（13）式右端和式僅有偶數下標部分的和，注意到：

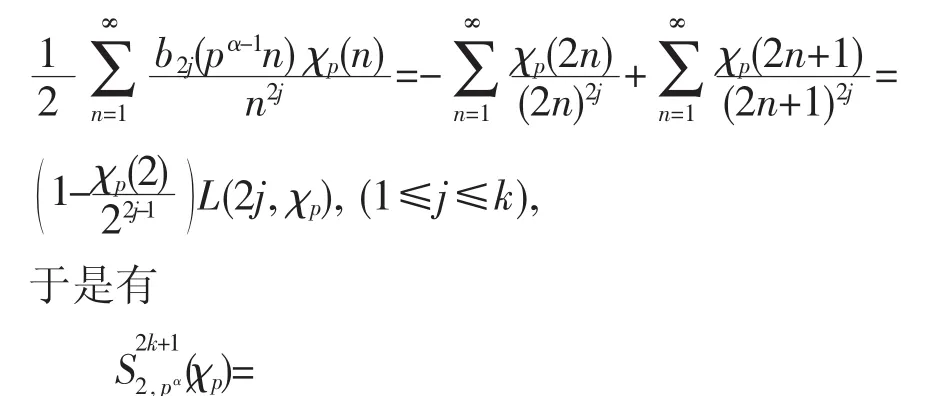
這就證明了(7)式，類似的可證明(8)式。

在引理1中，當時p≡3(mod4)，注意到pα≡(-1)α(mod 4)，取 t=1,u=4，則由(14)(15)式得：

將(13)式右端和式按下標的奇偶性分成兩部分，注意到：

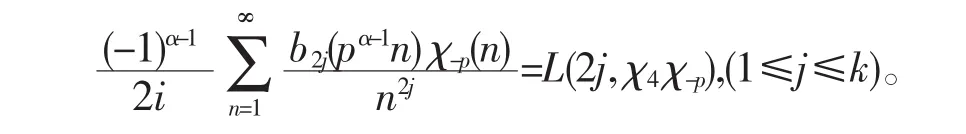
偶數下標部分的和為：

由(18)(19)式即得(9)式。類似的可證明(10)式。

要證明(11)式，取 t=1,u=2，則由(14)(15)式得：

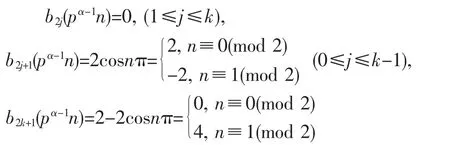
此時，(13)式右端和式僅有奇數下標部分的和，注意到：

這就證明了(11)式，類似的，可證明(12)式。

參考文獻：

[1]閔嗣鶴，嚴士健.初等數論[M].2版.高等教育出版社,2001.

[2]李子臣,戴一奇.二次剩余密碼體制的安全性分析[J].清華大學學報(自然科學版),2001,41(7)：80-82.

[3]WANG N L，LIJZ， LIU D S.EulerNumber Congruences and Dirichlet L functions[J].J Number Theory,2009,129：1522-1531.

[4]WANG N L，LI H L,LIU G D.CosineE Highter-order Euler number congruences and Dirichlet L-function values[J].Kyushu Journal of Mathematics,2017,71(1)：197-209.

[5]王念良,趙銳.交錯級數Euler變換式的一個應用[J].商洛學院學報,2013,27(2)：3-5.