數學復習課中需要明確的幾個要點

☉江蘇省海安縣曲塘中學 萬海兵

數學復習課中需要明確的幾個要點

☉江蘇省海安縣曲塘中學 萬海兵

數學從本質上來說是考查學生思維、培養(yǎng)學生能力的一門學科.高中階段的數學對學生思維水平的發(fā)展極其重要.我們學習數學的目的及高考考查學生的方向都是考查學生的思維能力.下面以函數復習為例，就其中需要明確的幾個要點，舉例說明.

一、做好知識的定位

數學復習，應從基礎知識開始，若知識不清楚，我們的復習就是沒有基礎的復習.但知識的復習不是死記硬背，特別是對于一些文科的考生來說，不能把數學的學習變成是記結論、記題型、記解法，這樣的復習只能是越復習越僵化，禁錮自己的思維.實際上思維不是記與不記的問題，而是我們思考的多與少的問題.

分析：本題是以基本初等函數中的冪函數為背景的分段函數問題，這就要求我們一定要熟悉最基本的函數的圖像及相關的性質.要弄清兩個函數y=x2與y=x3的異同：一個為偶函數，一個為奇函數；兩函數有兩個公共點（0，0），（1，1）.在區(qū)間（0，1）內，x2＞x3，在區(qū)間（1，+∞）內，x2＜x3.因此分段點的變化，決定了函數f（x）相關性質的變化.據此可得出如圖1～圖3所示的三種情況，問題的求解自然不攻自破了.

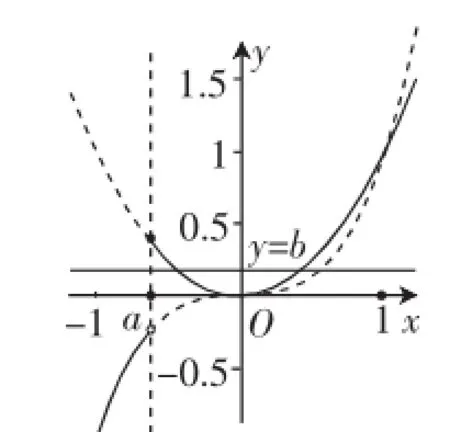
圖1

圖2

答案：（-∞，0）∪（1，+∞）

除此之外，指數函數、對數函數也是我們所學的最基本的函數，復習中在熟悉這些基本函數的前提下，還要善于將它們綜合起來考慮，如y=x-lnx，y=lnx x，y=x2-ex……這些函數的性質又是如何呢？

圖3

二、注重對知識本質的思考

數學知識的學習不僅僅是記定義、公式、法則，關鍵是要抓住本質.如：什么叫奇函數？學生的回答通常有兩種答案：①奇函數的圖像關于原點對稱.②f（-x）=-f（x）.這是奇函數概念下的兩個結論.一個是圖像特征，一個是符號語言.這兩個結論學生說出來，說對了.這是因為經過長期的復習，他記下來了.但這樣仍屬于不會思維，不會用函數的思維理解這個概念.正確的回答應該是什么呢？應該是自變量取了和為零的兩個值的時候，也就是相反數的時候，對應的函數值相反.這才符合函數的思維.

如果將“關于原點對稱”改為關于其他點對稱呢？

A.0B.mC.2mD.4m

三、明確思維能力提高的途徑

復習中我們大量做題的目的，實際上是要通過做題來找到科學的思維方法，通過做題找到解決數學問題的一般方法.到了高三的最后階段，其實解決問題的方法應該是越少越好.我們所用的方法應該是本質的，而不是形式的.如果我們在每一個單元的復習之后，都能找到解決問題的本質方法，那么我們就有信心參加高考了；如果越做題感覺自己的問題越多，甚至覺得有很多題沒有做，匆匆忙忙就去考試了，這樣就表明我們對于復習的理解與認識還不夠準確.

例3已知函數f（x）=x2-2x+2，g（x）=ax+lnx（a∈R），若存在x1∈［0，1］，x2∈［1，e］，使得f（x1）＜g（x2）成立，求實數a的取值范圍.（其中e為自然對數的底數）

總結：?x1∈D，x2∈E，f（x1）＜g（x2）?［f（x）］min＜［g（x）］max.

變式1：若?x1∈［0，1］，?x2∈［1，e］，使f（x1）＜g（x2）成立，求實數a的取值范圍.（其中e為自然對數的底數）

總結：?x1∈D，?x2∈E，f（x1）＜g（x2）?［f（x）］max＜［g（x）］max.

變式2：若?x1∈［0，1］，?x2∈［1，e］，使f（x1）=g（x2）成立，求實數a的取值范圍.（其中e為自然對數的底數）

總結：?x1∈D，?x2∈E，f（x1）=g（x2）?f（x）的值域?g（x）的值域.

變式3：若?x1∈［0，1］，?x2∈［1，e］，使f（x1）=g（x2）成立，求實數a的取值范圍.（其中e為自然對數的底數）.

總結：?x1∈D，?x2∈E，f（x1）=g（x2）?f（x）的值域∩g（x）的值域≠?.

變式4：若?x1∈［0，1］，?x2∈［1，e］，使f（x1）＜g（x2）成立，求實數a的取值范圍.（其中e為自然對數的底數）.

總結：?x1∈D，?x2∈E，f（x1）＜g（x2）?［f（x）］max＜［g（x）］min.

通過對上述例題進行一題多變可以看出，此類型題目中均含有兩個函數，并且含有兩個變量.由于這兩個變量在各自區(qū)間上的取值具有任意性，因此，這類問題最終轉化為函數值域或最值問題加以解決.

例4如圖4所示，A是函數f（x）=2x的圖像上的動點，過點A作直線平行于x軸，交函數g（x）=2x+2的圖像于點B，若函數f（x）=2x的圖像上存在點C使得△ABC為等邊三角形，則稱A為函數f（x）=2x上的好位置點.函數f（x）=2x上的好位置點的個數為（）.

A.0B.1C.2D.大于2

圖4

圖5

正確選項為B.

此題的命題背景是指數函數，綜合考查了平面幾何知識.在成功解答此題后，思考：如何將指數函數換為對數函數，是否可行呢？

變式如圖5，點A，B在函數y=log2x+2的圖像上，點C在函數y=log2x的圖像上，若△ABC為等邊三角形，且直線BC∥y軸，設點A的坐標為（m，n），則m=（）.

正確選項為D.

經過這樣的訓練，我們會解的不是一個題，而是一類題，我們分析問題、解決問題的能力自然會得到有效的提升.

四、加強對解題方法的提煉

假如說解決函數問題的方法有多種，如果我們不去提煉，一個一個地去嘗試，等試到最后一種方法也解不了的時候，只能放棄了，因為沒有其他方法了.其實，這幾種方法也許從本質上來說，就是一個方法，但是在復習的時候我們沒有注意到.也就是說，我們做了很多題目卻沒有注意提煉，沒有提煉思維方法，沒有提煉解決問題的方法.

研究函數的一般方法是什么呢？當我們看到函數解析式時，不用將其分類，無論是含有字母，還是含有參數，甚至是一個簡單的函數解析式，我們都要研究它的性質，畫出其簡單的示意圖，進而清楚我們要研究的對象.圍繞這樣的函數設計的任何問題都有辦法解決了.

例5已知π為圓周率，e=2.718…為自然對數的底數.

（2）求e3，3e，eπ，πe，3π，π3這6個數中的最大數與最小數.

圖6

進而可得3π＞π3，eπ＞πe，e3＞3e及3π＞eπ＞e3，π3＞πe＞3e，故所求的最大數為3π，最小數3e.

，則a，b，c的大小關系為（）.

A.a＜b＜cB.c＜b＜a

C.c＜a＜bD.b＜a＜c

正確選項為C.

很多學生在解題時，只是粗略地審題后，就直奔結果了，對于函數本身的理解很片面，這樣的話就會影響到解題的思路.所以解題的方法怎么來的？哪來的呢？你要把你的研究對象研究透徹.

總之，在數學復習時，不是從知識的角度去考慮哪些講了，哪些沒講的問題.而是關注最核心的知識、最核心的思維、最核心的方法.所以，我們在最后的這個階段，若仍不關注自己思考問題的方式，只是埋頭做題，那就可能喪失最佳的提高自己思維能力的機會.F