例談利用必要條件縮小參數范圍在解題中的運用
——從一道模擬題說起

☉江蘇省鹽城市伍佑中學 高小勇

例談利用必要條件縮小參數范圍在解題中的運用
——從一道模擬題說起

☉江蘇省鹽城市伍佑中學 高小勇

含參不等式的求解是近年來全國各地高考數學、競賽數學的考查熱點.這類問題既含參數又含變量，往往與函數、數列、方程、幾何等有機結合起來，常與不同知識交匯，其綜合性強，解法靈活，思維要求高，往往令很多同學望而生畏.學生解決此類問題往往力不從心，討論問題不全面.本文從一道模擬題開始談談如何利用必要條件來縮小范圍入手，優化解題過程.

一、題目再現

二、學生的解答思路展示

解法2：變量分離，將要求的式子轉化為a（1+xlnx）≥-xlnx，再轉化為

由此可知，學生在處理這類恒成立問題時的方法是沒有問題的，但是由于其中涉及分類討論，有時涉及的函數復雜，學生很難將問題進行到底.筆者結合學生遇到的實際問題，利用必要條件將范圍縮小后，優化了解題過程.

三、利用必要條件縮小范圍后的解法

解法1（直接構造含參函數）：f（x）≤x恒成立可轉化為a+（a+1）xlnx≥0恒成立.

令φ（x）=a+（a+1）xlnx，x∈（0，+∞），則φ（x）≥0對任意x∈（0，+∞）恒成立，那么φ（1）≥0，從而得到a≥0.

易知a=0不成立，所以a＞0，a+1＞1.

又因為φ′（x）=（a+1）（1+lnx），

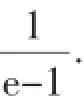
解法2（分離參數）：f（x）≤x恒成立可轉化為a+（a+1）· xlnx≥0恒成立，則（a+1）xlnx≥-a.

因為a+（a+1）xlnx≥0對任意x∈（0，+∞）恒成立，所以x=1滿足上述不等式，即a≥0.所以（a+1）xlnx≥-a可轉化為

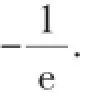
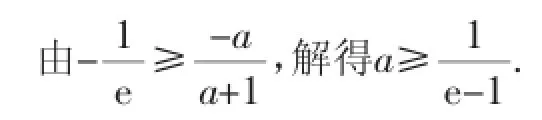
由上面兩種方法的對比可以看出，先利用題目所給范圍內的特殊值去縮小范圍，在求函數最值時就可以減少分類討論的情況，優化了解題過程.

這樣的例題很多，下面列舉幾例加以說明：

例1若不等式x2-2mx+2m+1＞0對滿足0≤x≤1的所有實數x都成立，求實數m的取值范圍.

解：設（fx）=x2-2mx+2m+1，則本題等價于函數（fx）在0≤x≤1上的最小值大于0，求實數m的取值范圍.

因為函數（fx）在0≤x≤1上的最小值大于0的必要條件是（f0）＞0，即2m+1＞0，也即

注：本題的解法一般是考慮m＜0，0≤m≤1，m＞1三種情況進行討論.

解：不等式成立的必要條件是0≤b≤1，a＞0.下面討論此條件成立.不等式x2+1≥ax+b轉化為x2-ax+（1-b）≥0對任意x∈［0，+∞）成立的充要條件是

令f′（x）=0，得x=a-3.

當0＜x＜a-3時，f′（x）＜0；當x＞a-3時，f′（x）＞0，所以，當x=a-3時，（fx）取最小值.因此，（fx）≥0成立的充要條件是（fa-3）≥0，即a≥（2b）-12.

注：由于利用不等式成立的必要條件把a，b的取值范圍縮小，使問題在一個較小的范圍內進行解決，使得解題的難度大大降低.

例3設函數（fx）=x（ex-1）-ax2.若當x≥0時，（fx）≥0，求實數a的取值范圍.

解：函數（fx）可化為f（x）=x（ex-1-ax）.根據不等式ex≥x+1，顯然當a=1時，（fx）≥0成立，故a=1是不等式成立的必要條件.令g（x）=ex-1-ax，則g（′x）=ex-a.若a≤1，則當x∈（0，+∞）時，g′（x）＞0，g（x）為增函數，而g（0）=0，從而當x≥0時，g（x）≥0，即（fx）≥0.

若a＞1，則當x∈（0，lna）時，g′（x）＜0，g（x）為減函數，而g（0）=0，從而當x∈（0，lna）時，g（x）＜0，即（fx）＜0.

綜合得實數a的取值范圍為（-∞，1］.

注：發現a=1是不等式成立的必要條件，找到分類討論的標準，為破解難題創造條件.

例4已知函數（fx）=ax2-lnx（a為常數）.

（2）若a＜0，且對任意的x∈［1，e］，（fx）＞（a-2）x恒成立，求實數a的取值范圍.

解：（1）略.

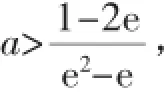
由此看出，恒成立問題作為高中階段非常重要的一個問題，在掌握了解決恒成立問題的基本方法后，再結合特殊值縮小參數的范圍可以大大簡化問題的難度，增加學生的解題經驗.