理想通信條件下彈星協同定位方法*

段佳珍，曹菲，白福忠

(火箭軍工程大學，陜西 西安 710025)

理想通信條件下彈星協同定位方法*

段佳珍，曹菲，白福忠

(火箭軍工程大學，陜西 西安 710025)

為了提高彈載電子偵察設備的定位精度，對目標實施更精確的打擊，提出了理想通信條件下的彈星協同定位方法，對基于概率的定位原理進行了分析，對定位系統的架構及定位流程做了說明，并在STK中做了仿真演示，提出基于概率的彈星協同定位算法，給出了該算法的數學推導，并對算法進行了仿真實驗，驗證了該算法的有效性并對算法性能做了一定分析。

電子戰；協同定位；相位干涉儀；模糊相位差；最大后驗概率；STK

0 引言

隨著電子戰水平的迅速提高，電子戰在現代戰爭中起著越來越重要的作用[1]。對敵輻射源進行精確定位，是反輻射武器高效能打擊的前提。但是，電子偵察設備面臨的電磁環境日趨復雜，不易實現對目標的精確定位，想要改善設備性能則成本大、耗時長，考慮到空天偵察技術的大力發展，衛星資源越來越豐富，且衛星具有偵察范圍廣，不受氣候影響等得天獨厚的優勢，因此，在保證時間窗口的條件下，利用衛星與導彈協同定位[2]可以很大程度上提高對目標的定位精度，在實際作戰中有非常重大的意義。

1 基于概率的定位原理

通過觀測站被動接收非合作輻射源信號并確定其位置的無源定位技術在偵察、監視、預警等領域受到廣泛關注和研究[3]。在無源定位技術中，常采用測向交叉定位法[4]，即利用運動觀測器多次測量信號來波方向(direction of arrival,DOA)的交叉實現對輻射源定位。為了能夠更精確測量DOA，常采用相位干涉儀法[5]測向，但當基線長度大于信號半倍波長時，干涉儀相位差的測量會出現2nπ模糊從而導致測向模糊，受直接利用信號估計輻射源位置的直接定位(direct position determination，DPD)方法[6]的啟示，用概率的思維，考慮直接利用干涉儀鑒相器輸出的模糊相位差實現對輻射源目標的定位，如圖1所示。

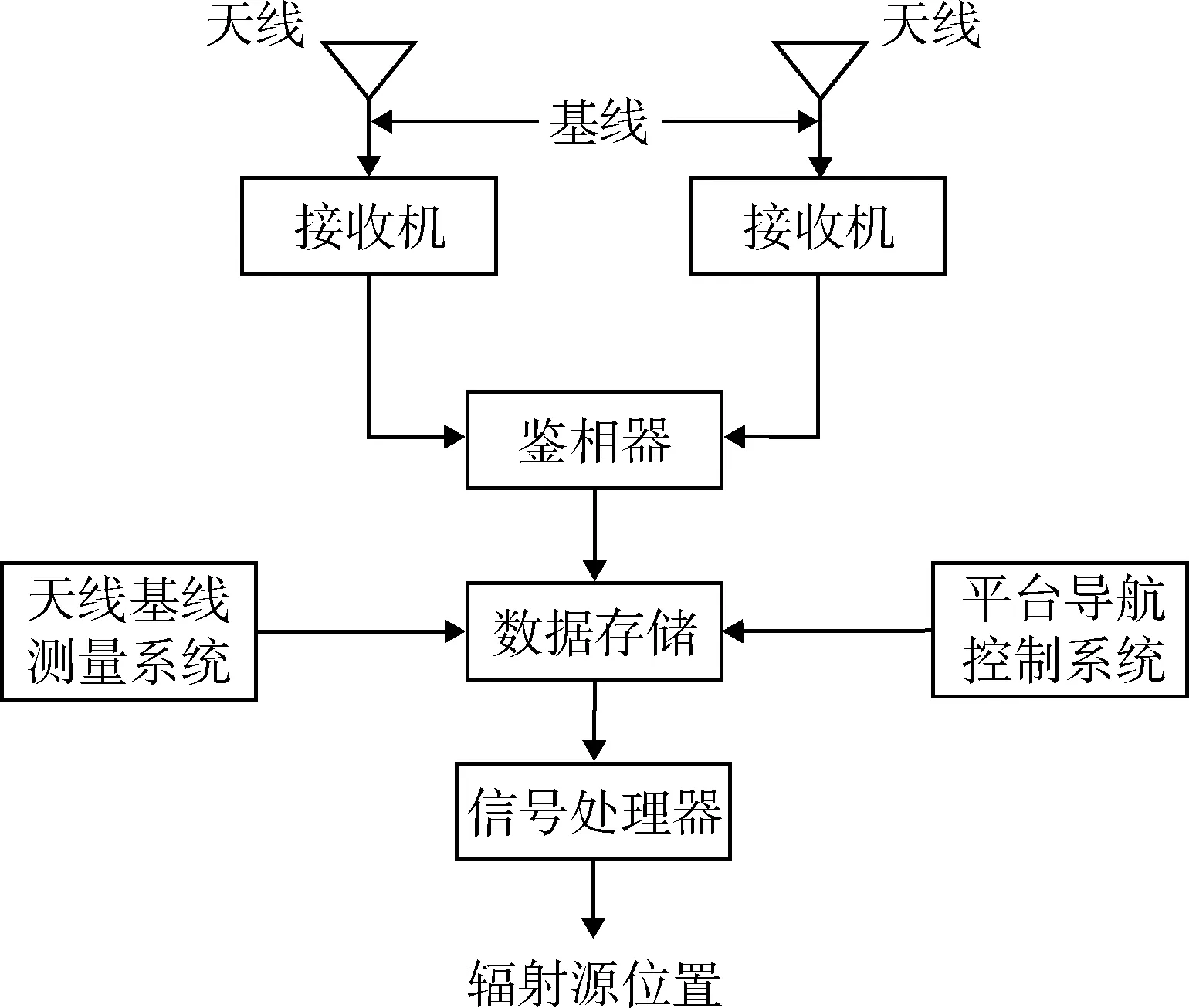
圖1 定位原理框圖Fig.1 Block diagram of localization principle

無源定位系統每一次測量可以給出一個定位子集，設該子集為M。由于存在測量誤差，那么輻射源有可能不在M之內，但這種情況發生的概率要遠遠小于落在M之內的概率，那么就可以用概率的思維來分析定位問題。在每一次測量中，輻射源隨機分布在衛星偵察區域的任一位置上，但分布在各位置上的概率是不同的，分布在M內的概率要比分布在M外的概率大，并且離M越遠，分布概率越小。經過多次測量后就會得到多個定位子集，每一個定位子集對應目標可能落在某一位置上概率密度。一般來說，每次測量都是獨立、不相關的，那么目標落在某一具體位置的概率就是每次測量對應的概率之積。

假設某個觀測量W的測量值為W0，用概率密度函數來描述觀測量W的分布

(1)

觀測量W對應一個子集，設輻射源坐標點與測量值之間的關系為

f(x,y,z)=W.

(2)

將f(x,y,z)展開為泰勒級數和的形式

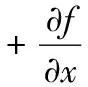
(3)

那么式(1)變為

(4)

這樣，就把概率密度函數與坐標聯系在一起。此時，“定位”的概念就稱為從已知的觀測量中求取在概率意義上最可能的一個空間坐標。

多次測量的概率密度函數通常由單次測量的概率密度函數相乘產生。即總概率密度函數指數為

FT(x,y,z)=∑Fi(x,y,z).

(5)

由于指數函數是單調函數，那么總概率密度函數的峰值是存在且唯一的。并且從上面的分析可知，總概率密度函數峰值的位置就是輻射源的位置。

2 彈星協同定位架構及流程[7]

如圖2所示，整個定位系統由導彈、衛星及敵輻射源目標組成，假設導彈與衛星可視即可通信，且收發順利。

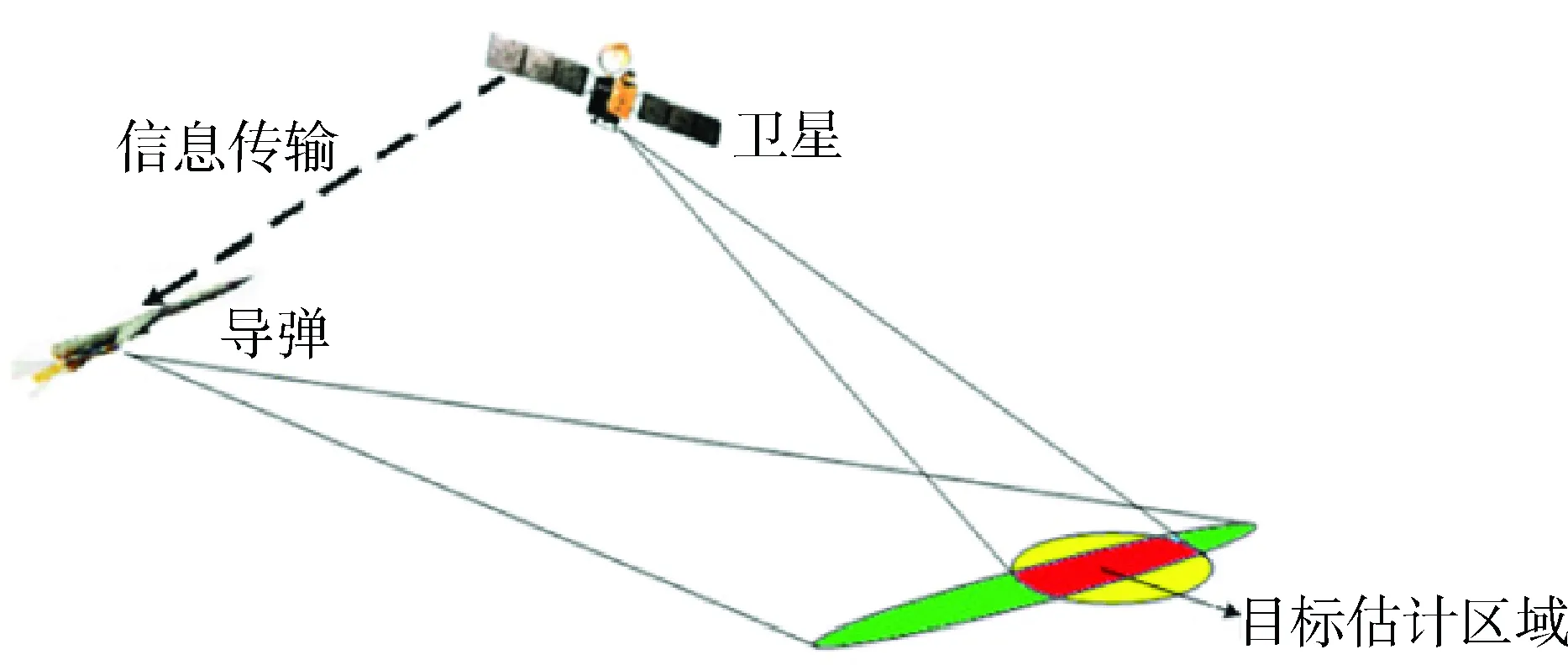
圖2 彈星協同定位示意圖Fig.2 Sketch map of missile-satellite co-location

導彈在飛行過程中接收到的來自衛星的敵輻射源目標信息，能夠協助導彈更好地跟蹤目標，實施精確打擊，具體流程[8]如圖3所示。

圖3 彈星協同定位流程圖Fig.3 Flow chart of missile-satellite co-location

導彈作為協同發起者，主導整個協同過程[9]。衛星對目標區域實施不間斷偵察，導彈在指定時間、指定地點發射后，滿足時間窗口的衛星在一段時間內為其實時傳輸目標參數信息，導彈將自身雷達探測到的目標參數信息與衛星提供的信息進行融合處理，解算出目標位置，保證實現精確打擊[10]。

3 基于最大后驗概率的彈星協同定位算法

基于概率的彈星無源定位算法[11]是以干涉儀輸出的模糊相位差[12]為信息依據，無需解相位模糊，即可實現對輻射源的精確定位，具有定位精度高、速度快和穩定性好的優點。

3.1 目標估計區域確定

根據目標的先驗信息、導彈的飛行軌跡、衛星的軌道，可以先確定一個以衛星星下點為中心的初始目標搜索區域。為減小后驗概率的計算量，把該區域均勻細分為n個子區域，子區域大小為(ΔL，ΔB)，并取各子區域的中心點作為后驗概率的計算點，如圖4所示。

3.2 后驗概率計算

在ECF坐標系下，以導彈為例，如圖5所示，導彈位置矢量： S=(sx,sy,sz)；導彈天線位置矢量： M=(mx,my,mz)。導彈位置矢量和導彈天線位置矢量可以通過北斗衛星導航系統(Beidounavigitionsatellitesystem,BDS)測量獲得，精度可滿足本系統的使用要求。設目標估計區域內任意一點T=(tx,ty,tz)，干涉儀輸出相位差[13]為

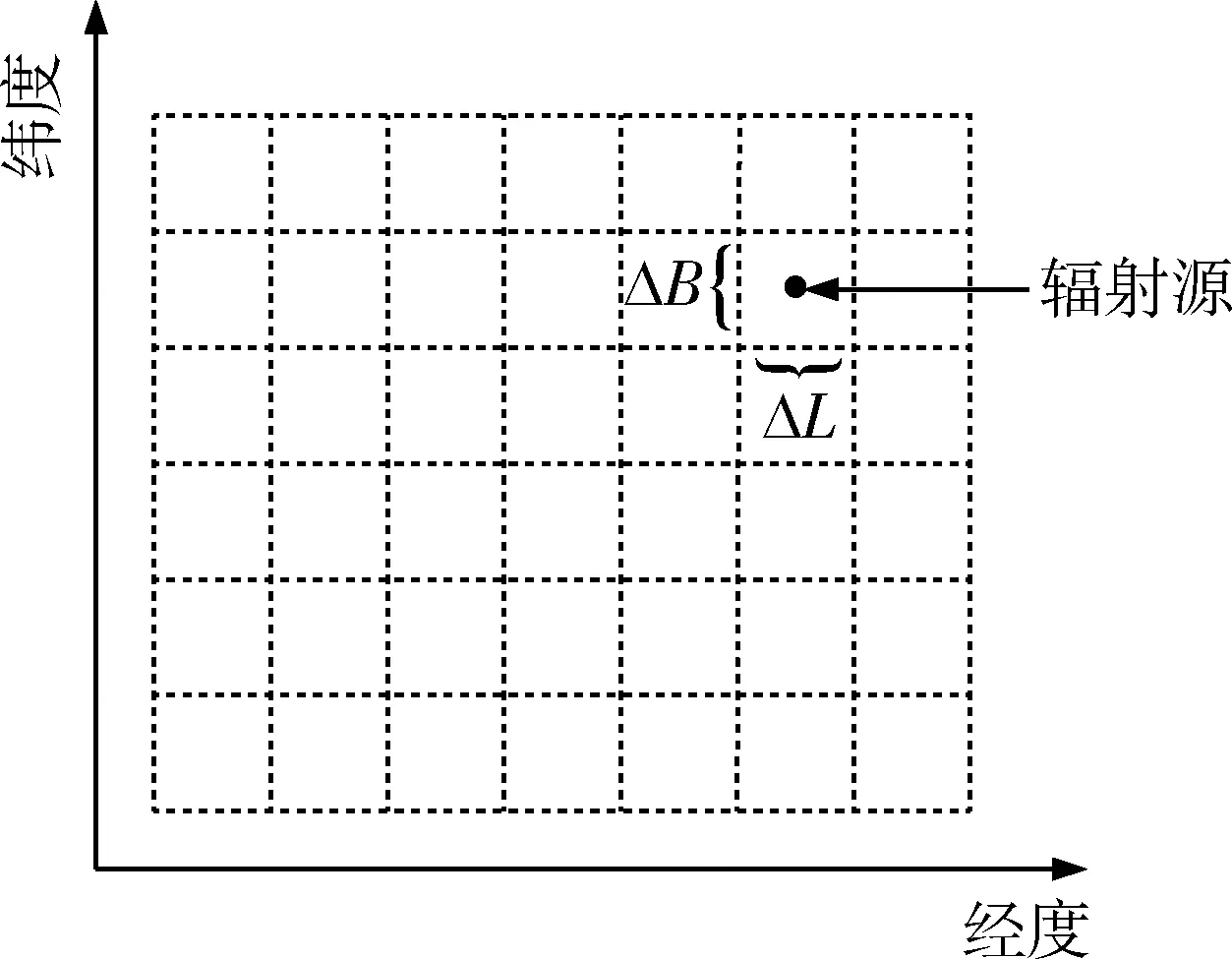
圖4 細分目標區域圖Fig.4 Subdivision of target area

(6)

式中：d為干涉儀基線的長度；λ為目標輻射源的波長；n為模糊數，并且

cosθ=[(tx-sx)mx+(ty-sy)my+

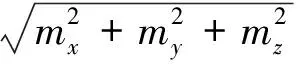
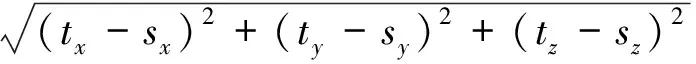
(7)

在(tx,ty,tz)處干涉儀輸出相位差φ的值受sx,sy,sz,mx,my,mz,λ的影響是獨立的，那么由式(6)可得

P[φ/(tx,ty,tz)]=P(sx)P(sy)P(sz)·

P(mx)P(my)P(mz)P(λ).

(8)

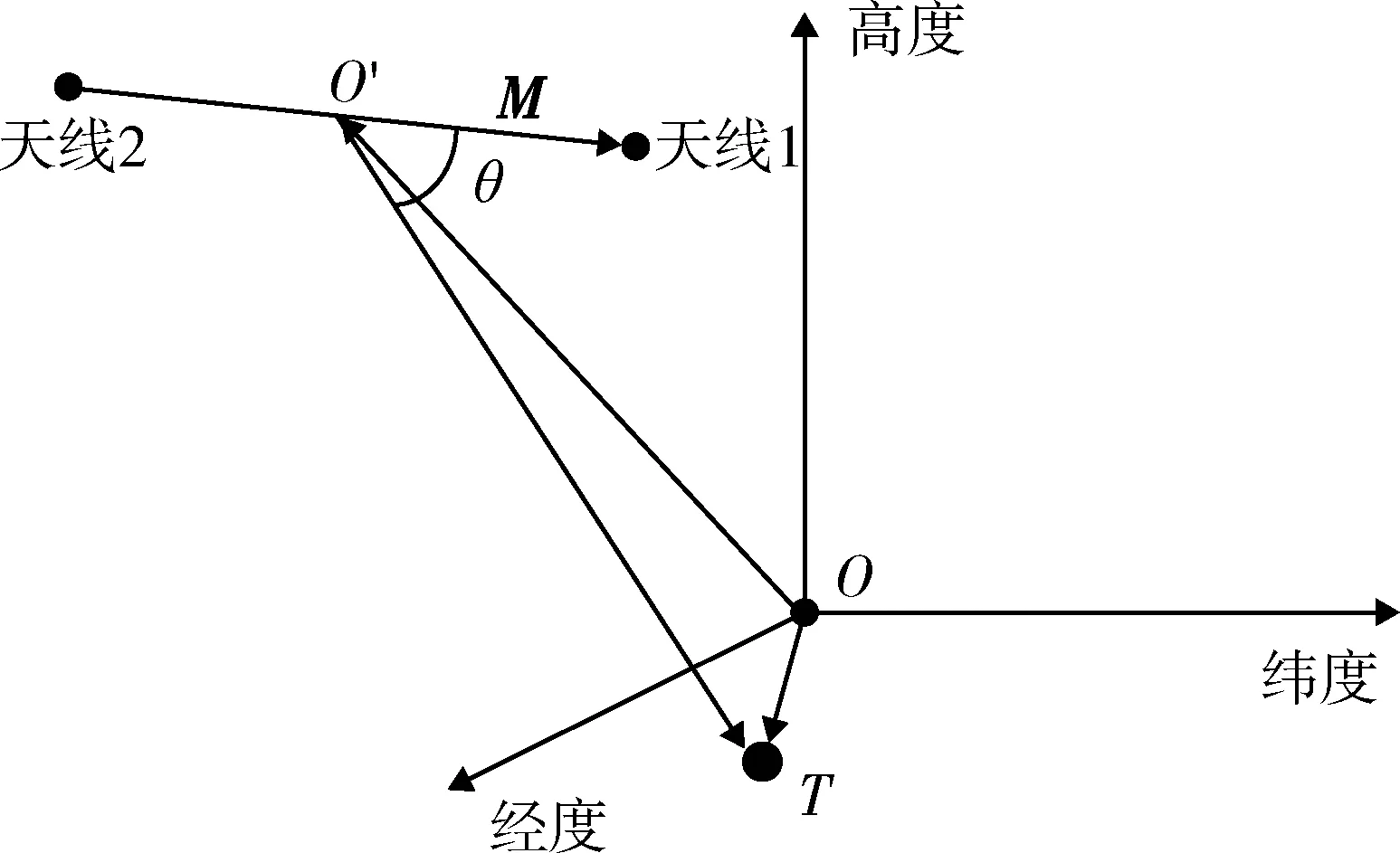
圖5 平臺搭載干涉儀模型圖Fig.5 Model diagram of platform borne interferometer

目標在目標估計區域內概率相等，設干涉儀測量的相位差為φm(模糊相位)，計算后驗概率為

P[(tx,ty,tz)/φm]=P[(tx,ty,tz)]·

P[φm/(tx,ty,tz)]·[∫P[φm/(tx,ty,tz)]dδ]-1.

(9)

設干涉儀測量相位差的誤差是均值為0的高斯白噪聲，則

φm～N(φ,σ2),

(10)

式中：φ為真值;σ為測量誤差的標準差。

因此

P[φm/(tx,ty,tz)]=P(φm/φ)P[φ/(tx,ty,tz)]=

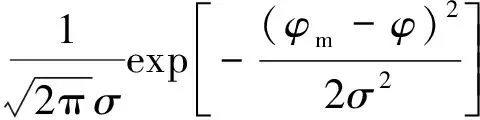
P(sx)P(sy)P(sz)P(mx)P(my)P(mz)P(λ).

(11)

則

P[(tx,ty,tz)/φm]=

P(sz)P(mx)P(my)P(mz)P(λ)ΔLΔB·

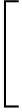
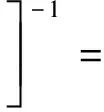
(12)

式(12)的分母積分后是一個常數值，設

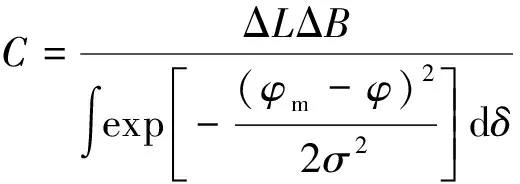
(13)

相位干涉儀在一段時間內經過N次觀測后得到φN=[φ1,φ2,…,φN]，φN在(tx,ty,tz)的后驗概率為

(14)

式中：C為常數。

不失一般性，設C=1，那么

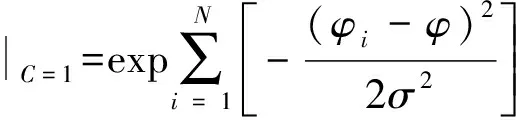
(15)

在實際應用中，測量誤差較大時

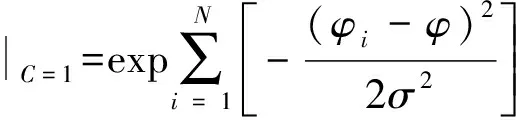
不便于數據處理。因此用概率累加的方式代替概率累積，將式(14)修改為

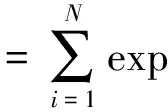
(16)

稱其為偽后驗概率。而偽后驗概率最大的點即為目標位置的估計點。

4 仿真實驗

4.1 彈星協同仿真演示

在STK中仿真[14]如下：如圖6所示，電子偵察衛星LD-1，LD-2，LD-3，LD-4，QS-1，QS-2，QS-3按預定軌道飛行，DF導彈發射點(108.985 E，19.176 N)，目標艦船(T)起始位置(94.6031 E，5174 N)，導彈于2016-4-5 T 04:25:20發射。

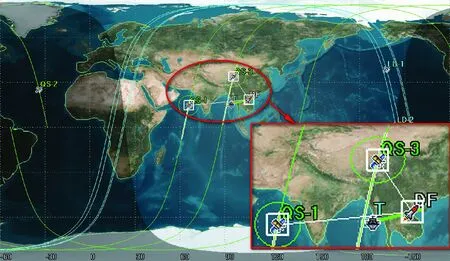
圖6 彈星通信示意圖Fig.6 Schematic diagram of missile-satellite communication

如圖7，8所示，7顆衛星中有2顆衛星滿足通信要求，可通信時間分別為440 s和675 s。

圖7 導彈與QS-1星通信時間Fig.7 Communication time between missile and QS-1

圖8 導彈與QS-3星通信時間Fig.8 Communication time between missile and QS-3

在已知衛星軌道方程情況下，只要時間確定，就可以求得衛星的位置點，那么衛星的覆蓋范圍也就已知了，如圖9所示。

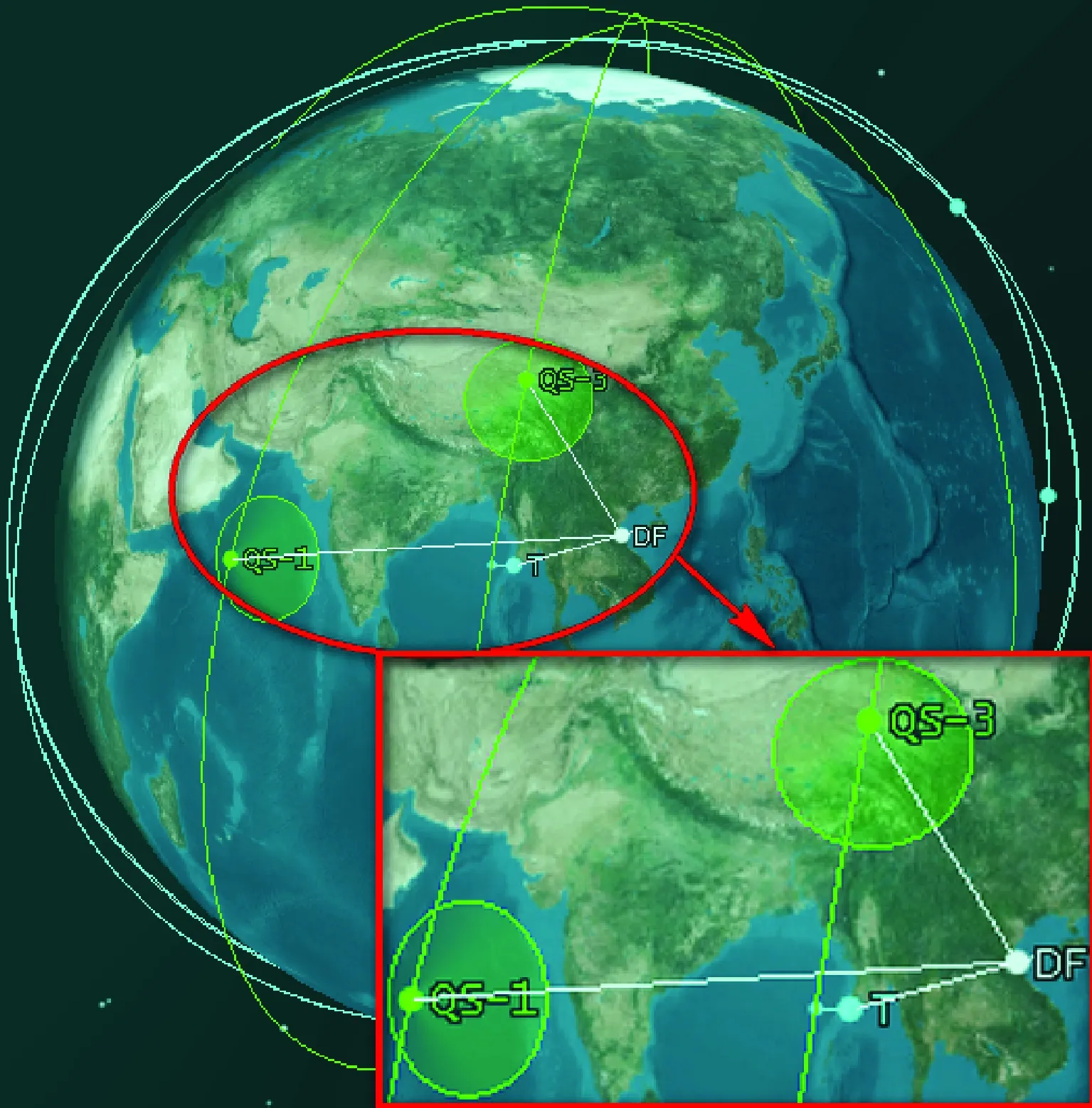
圖9 衛星偵察區域示意圖Fig.9 Schematic diagram of satellite reconnaissance area

如圖10所示，滿足通信條件的2顆衛星中只有QS-3可以偵察到目標區域且該時間段與導彈飛行時間重疊，因此QS-3滿足與導彈協同定位的條件。

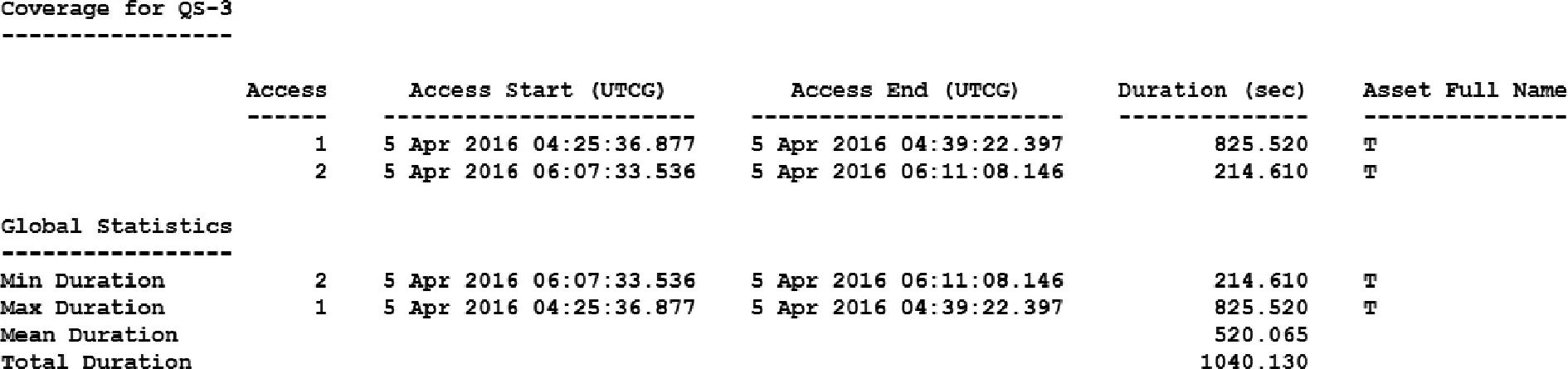
圖10 衛星偵察目標區域時間Fig.10 Time of satellite reconnaissance on target area

4.2 算法仿真案例

4.2.1 參數設置

導彈：導彈發射點坐標為(104.8 E，35.9 N，0 km)，數據更新間隔為0.1 s，基線波長比為5，相位差測量誤差為均方根10°的零均值高斯白噪聲。

衛星：軌道高度483 km，軌道傾角為45°，數據更新間隔為0.1 s，初始基線方向與衛星速度方向相同，基線波長比為5，相位差測量誤差為均方根10°的零均值高斯白噪聲。

敵輻射源：位于(129.5 E，32.9 N，0 km)，輻射的信號頻率為1.5 GHz。

目標估計區域：123 E～135 E，27 N～39 N。

4.2.2 仿真實現[15]

(1) 采用100組相位差

ΔL=ΔB=0.5°，圖11中概率峰值確定的目標位置為(129 E，33.5 N)。與實際目標位置相差(0.5 E,0.6 N),這個結果雖然可以證明算法的有效性，但誤差還是比較大的，想要得到更精確的結果，必須增大數據采集量，縮小子區域間隔。

從圖12可以看出定位點相對比較集中，因此，可以縮小目標估計區域以減小接下來仿真的計算量。

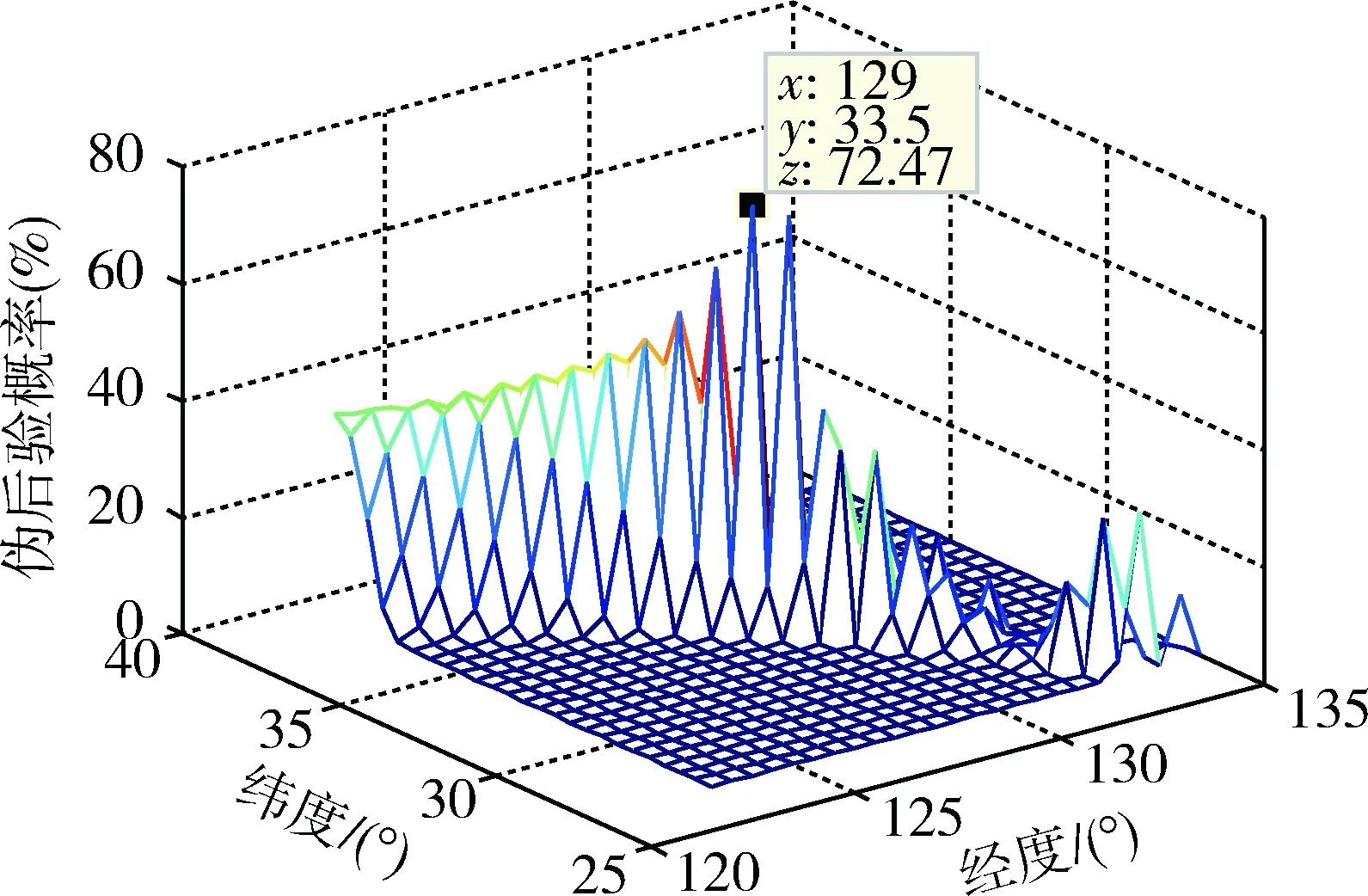
圖11 偽后驗概率分布圖Fig.11 Pseudo posterior probability distribution map

圖12 等概率示意圖Fig.12 Sketch map of equal probability

(2) 采用400組相位差

將目標估計區域縮小為127 E～131 E，31 N～35 N。

ΔL=ΔB=0.2°。由圖13可以得到目標估計位置為(129.4 E，33.2 N)，與實際目標位置偏差(0.1 E，0.3 N)，由此可以看到，隨著數據量的增大和子區域間隔的減小，定位更精確。

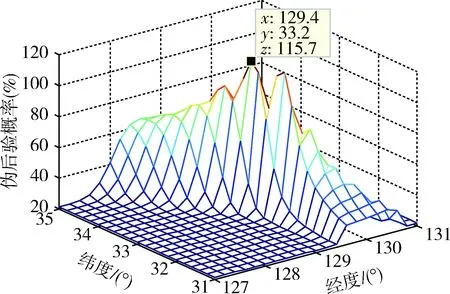
圖13 偽后驗概率分布圖Fig.13 Pseudo posterior probability distribution map

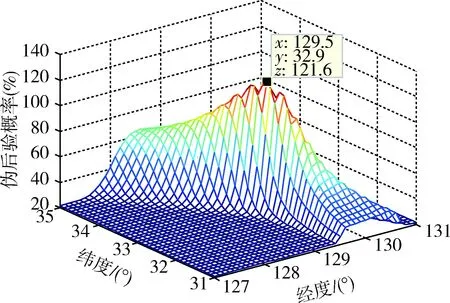
圖14 偽后驗概率分布圖Fig.14 Pseudo posterior probability distribution map

ΔL=ΔB=0.1°。由圖14可以得到目標估計位置為(129.5 E，32.9 N)，與實際目標位置一致。由此可見，子區域分割越精細，確實可以得到更精確的定位結果，但是定位時間相對也會延長。

(3) 100次蒙特卡羅仿真

1) 100組相位差

仿真結果見圖15，定位均值為(129.480 7 E，32.927 5 N)，定位均值與真實目標位置偏差3.544 km，定位的圓概率誤差為22.2 km。

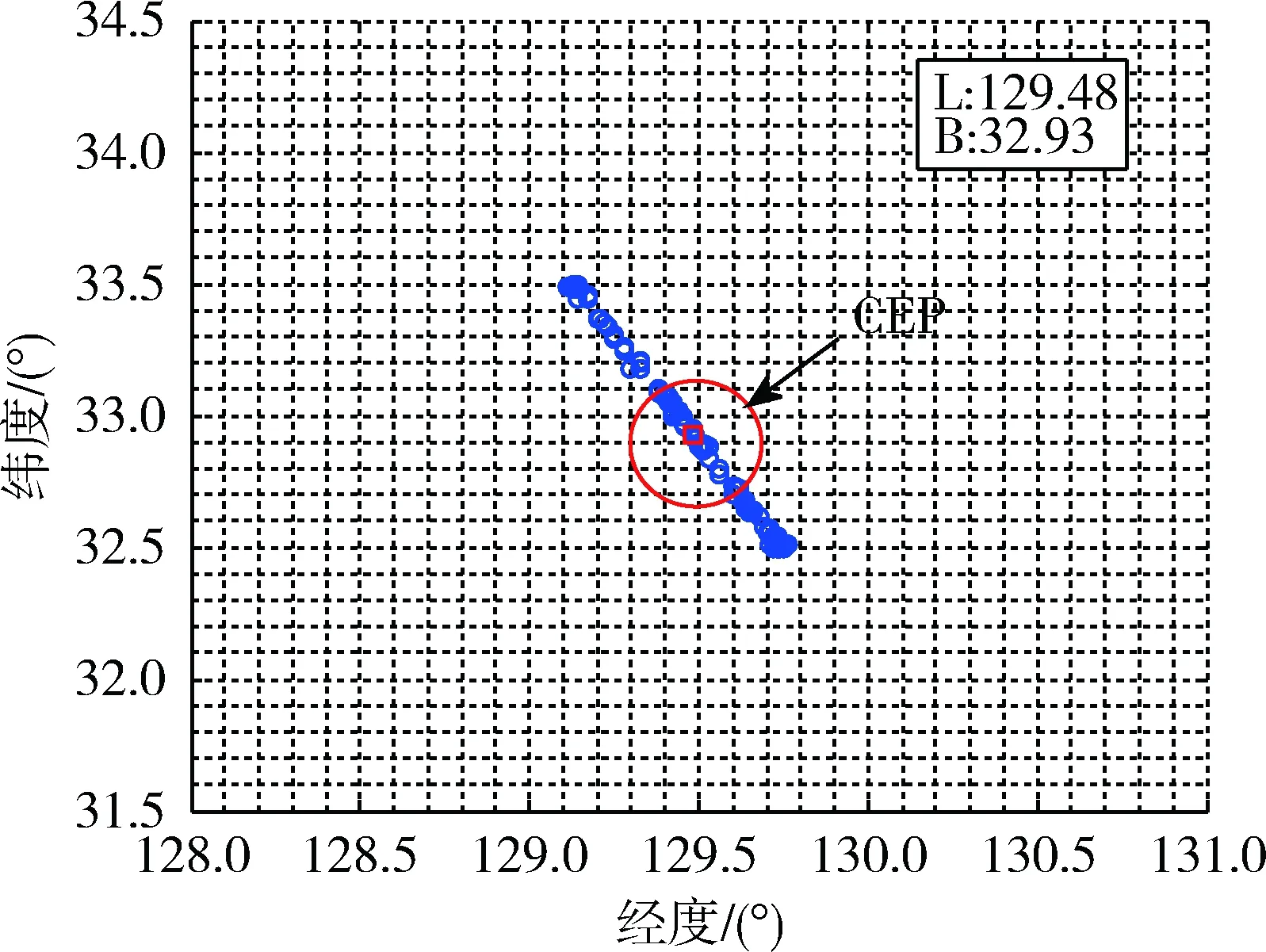
圖15 定位結果分布圖Fig.15 Localization result distribution map

2) 400組相位差

仿真結果見圖16，定位均值為(129.496 3 E，32.905 5 N)，定位均值與真實目標位置偏差0.701 km，定位的圓概率誤差為9.99 km。

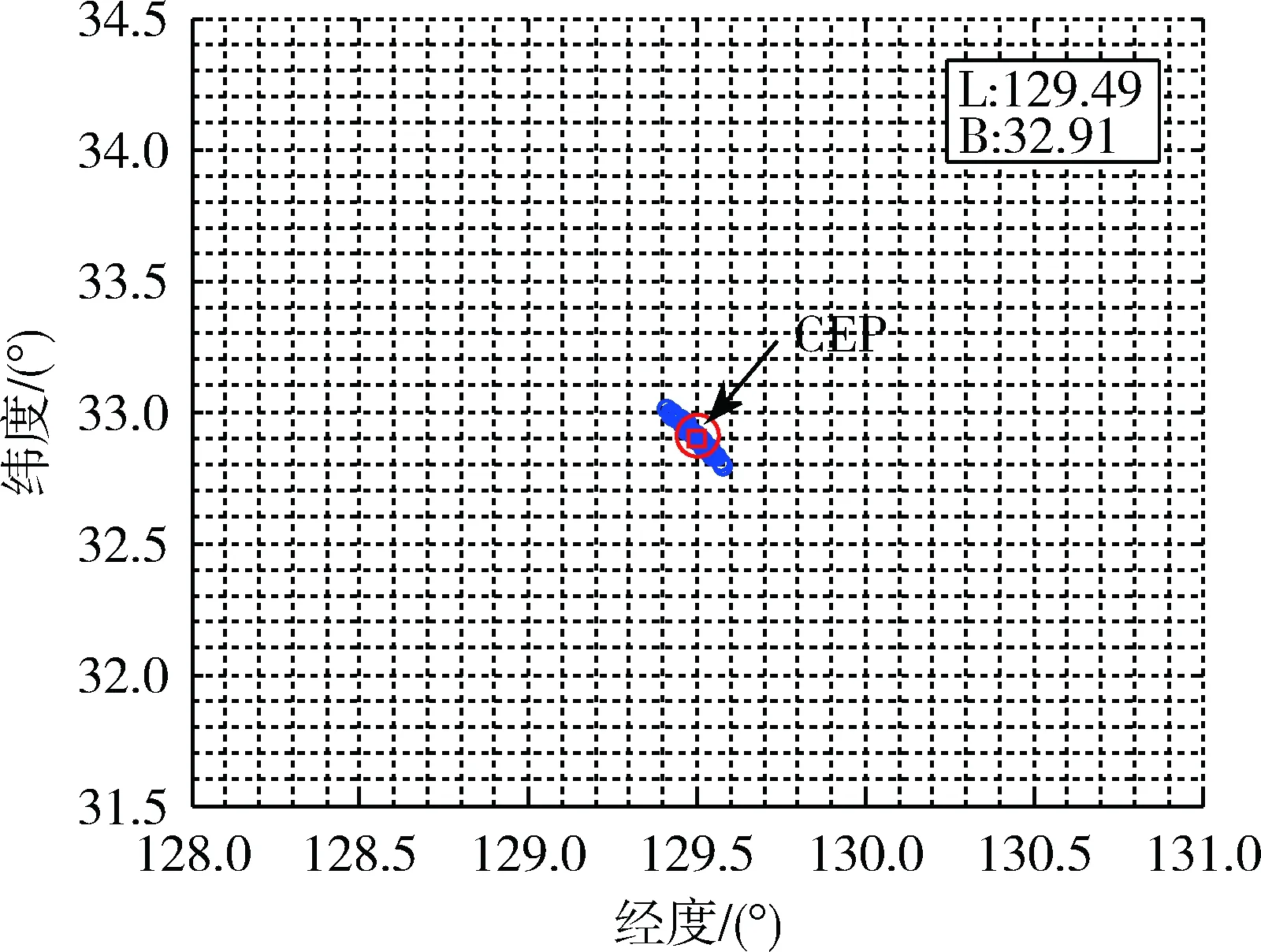
圖16 定位結果分布圖Fig.16 Localization result distribution map

由仿真結果可以看到利用最大后驗概率算法，的確可以實現對目標的精確定位，且隨著子區域間隔的減小和數據量的增大，定位精度越來越高。

為了減小測量誤差對定位結果的影響進行的100次蒙特卡羅仿真實驗表明，數據量為100時，采集數據時間為10 s，圓概率誤差為22.2 km，數據量為400時，采集數據時間為40 s，圓概率誤差為9.99 km，由此可得，可利用數據量越大，定位精度越高，導彈與衛星協同可以在相同時間內得到2倍的數據量，很大程度上提高了對目標的定位精度。

5 結束語

本文針對反輻射導彈對目標定位精度不足的問題，介紹了理想通信條件下彈星協同定位架構、定位流程及定位算法，并對算法進行了仿真，證明了該算法的有效性。實際戰場情況復雜，想要實現彈星協同定位，必須依賴于豐富的衛星資源和合理的任務調度，相信隨著軍隊現代化的發展，大規模、跨平臺聯合作戰能夠很快實現。

[1] 龍寧.單星無源定位原理及精度分析[J].電訊技術，2012，52(6)：17-20. LONG Ning.Single Satellite Passive Localization Principle and Precision Analysis[J]. Telecommunication Engineering, 2012,52(6)：17-20.

[2] 劉俊成,張京娟,譚麗芬.新的導彈協同定位技術[J].北京航空航天大學學報，2012,38(9)：1149-1153. LIU Jun-cheng,ZHANG Jing-juan,TAN Li-fen.New Techneque for Multi-Missile Cooperative Localication[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012,38(9)：1149-1153.

[3] RONG Y, PEK H F. RF Emittr Geolocation Using Ampllitude Comparison with Auto-Calibrated Relative Antenna Gains[J].IEEE Transactions on Aerospace and Electronic System, 2011,47(3):2098-2110.

[4] 王國剛.兩站測向交叉定位相對誤差幾何稀釋度研究[J].艦船電子工程,2015(12):58-61. WANG Guo-gang.Relative Geometric Dilution of Precision in Double Station Bearing-only Location[J].Ship Electronic Engineering, 2015(12):58-61.

[5] MACPHIE R H, YOON T H. On Using the Compound Interfermeter to Obtain the Power Pattern of a Conventional Receiving Array[J]. IEEE Transactions on Antennas and Propagation,2009,57(10):3356-3359.

[6] WEISS A J. Direct Geolocation of Wideband Emitter based on Delay and Doppler[J].IEEE Transactions on Signal Processing,2011,59(6):2513-2521.

[7] 彭銳暉，王國宏，陳士舉，等.兩彈協同定位的可行性研究[J].系統仿真學報,2006,18(5)：1118-1122. PENG Rui-hui,WANG Guo-hong,CHEN Shi-ju,et al.Feasibility Research on Two Missiles’Cooperative Location[J].Journal of System Simulation, 2006,18(5)：1118-1122.

[8] 萬華.多傳感器協同定位技術[J].艦船電子對抗,2014,37(3)：30-32. WAN Hua.Research into Multi-Sensor Cooperative Location Technology[J].Shipboard Electronic Countermeasure, 2014,37(3)：30-32.

[9] CACERES M A, PENNA F, WYMEERSCH H, et al. Hybrid Cooperative Positioning Based on Distributed Belief Propagation[J]. IEEE Journal on Selected Areas in Communications, 2011, 29(10): 1948-1958.

[10] DAS K, WYMEERSCH H. Censored Cooperative Positioning for Dense Wireless Networks[C]∥Proceedings of 2010 IEEE 21st International Symposium on Personal, Indoor and Mobile Radio Communications Workshops (PIMRC Workshops),2010:262-266.

[11] 胡來招.無源定位[M].北京：國防工業出版社，2004:31-79. HU Lai-zhao. Passive Locating[M].Beijing:Nationa Defence Industry Press, 2004:31-79.

[12] 劉建林. 多站無源定位技術研究與應用[D]. 西安：西安電子科技大學, 2011. LIU Jian-lin.Research and Application of Multi Station Passive Location Technology[D].Xi’an: Xi’an Electronic Technology University,2011.

[13] 盧厚清，宋歌，陳卓，等.基于逐點交匯的雙星無源定位方法及誤差分析[J].解放軍理工大學學報:自然科學版, 2013,14(6)：597-602. LU Hou-qing,SONG Ge,CHEN Zhuo, et al. Double-satellite Passive Location Method and Error Analysis Based on Point By Point Intersection[J]. PLA University of Science and Technology:Natural Science ed,2013,14(6)：597-602.

[14] 楊彬，張順健，方勝良，等.基于STK的衛星覆蓋模型研究與仿真分析[J].艦船電子對抗,2016(1)：66-71. YANG Bin, ZHANG Shun-jian,FANG Sheng-liang,et al.Research and Simulation Analysis of Satellite Coverage Model Based on STK[J]. Shipboard Electronic Countermeasure, 2016(1)：66-71.

[15] 倪天權，王春波，張殿友.兩艦協同定位誤差分析的研究[J].江蘇科技大學學報:自然科學版,2008,22(2)：11-14. NI Tian-quan,WANG Chun-bo,ZHANG Dian-you. Research on Cooperative Locating Error between Two Ships[J].Journal of Jiangsu University of Science and Technology: Natural Science ed, 2008,22(2)：11-14.

Missile-Satellite Co-Location Technology Based on Ideal Communication Condition

DUAN Jia-zhen, CAO Fei, BAI Fu-zhong

(Rocket Force University of Engineering, Shaanxi Xi’an 710025, China)

In order to improve the localization precision of airborne electronic reconnaissance equipment, missile-satellite co-location method is proposed. Firstly, the principle of this method is analyzed. Secondly, the structure and process of location system is explained and simulated in STK. Finally, a location algorithm based on the posterior probability maximization principle is recommended, and a mathematical derivation is given. Simulation results show that the algorithm is efficient and robust, and the localization performance is related with the size of the data quantity.

electronic warfare; co-location; phase interferometer; fuzzy phase difference; maximum posterior probablity; STK

2016-04-21；

2016-06-21 作者簡介：段佳珍(1989-)，女，甘肅蘭州人。碩士生，主要從事雷達電子對抗方面的研究。

10.3969/j.issn.1009-086x.2017.02.012

P228.1;TP391.9

A

1009-086X(2017)-02-0080-07

通信地址：710025 陜西省西安市灞橋區同心路2號4502分隊 E-mail：dbojue1989@163.com