基于滑模變結構控制的感應電機系統容錯控制
卞高峰,沈艷霞
(江南大學,無錫214122)
0 引 言
感應電機因其良好的運行性能和低成本,被廣泛應用于工業系統中,例如機床、造紙等[1]。感應電機系統包含電力電子變換裝置,電動機,傳感器以及控制器,其中傳感器是控制系統中最為脆弱的環節。在一些惡劣的環境中(如高溫、潮濕、易燃易爆等),速度傳感器變得更加脆弱,發生故障時,如不及時處理會造成損失,甚至人員傷害[2],因此對傳感器進行故障診斷是非常必要的。另外,在一些特殊的應用場合(如航天、軍事、鋼鐵廠等),即使診斷出傳感器故障,也無法立即停機維修,仍需維持運行。此時研究對傳感器故障的容錯控制策略,尋找一種不依賴于速度傳感器的閉環控制方式,保證系統的繼續運行,意義重大。
傳感器的故障診斷方法大體分為兩種:一種是硬件法,另一種是軟件法[3]。硬件法具有診斷速度快,不占用軟件資源的特點,但增加系統成本且只適用特定類型的傳感器。相比較硬件法,軟件法不增加硬件成本,適用范圍廣,更具應用價值。而軟件法又可細分為基于知識和基于模型等方法。基于知識的方法需要大量先驗知識和數據。基于模型的方法更為普遍,而基于模型的方法關鍵就是數據重構,通過重構數據與傳感器測量信號進行比較,實現故障診斷。數據重構的方法有很多種,如自適應觀測器[4]、擴展卡爾曼濾波觀測器[5]、龍貝格狀態觀測器[6]等。文獻[4]基于旋轉坐標系下的定子電流模型采用參考自適應方法重構轉速,提高了低速估計性能,但由于存在純積分環節,積分初值和偏移會帶來誤差。文獻[5]采用擴展卡爾曼濾波法,該方法涉及協方差計算,且實際應用時需要了解誤差和噪聲特性。文獻[6]采用龍貝格狀態觀測器,該方法對參數變化的魯棒性較差。相比上述方法,滑模觀測器對模型要求低、結構簡單、計算量小,且具有較強的魯棒性[7]。但滑模觀測器也存在一個限制其應用問題,由于其本質上是不連續控制特性,會引起系統的抖振現象。
本文利用滑模變結構控制理論建立不依賴轉速的滑模磁鏈觀測器,根據李雅普諾夫理論證明觀測器的穩定性,并且對控制函數進行連續化處理和低通濾波減少抖振,改進觀測器性能。基于改進后的觀測器結合等效控制原理重構轉速信號。利用估計轉速信號對速度傳感器信號進行狀態監測,當檢測出故障時,用估計轉速代替傳感器信號作為系統新的反饋,保障系統的連續運行,從而實現對速度傳感器的容錯控制。
1 電機數學模型
電機是一個高階非線性系統,在靜止坐標系下的感應電機的數學模型[8]:
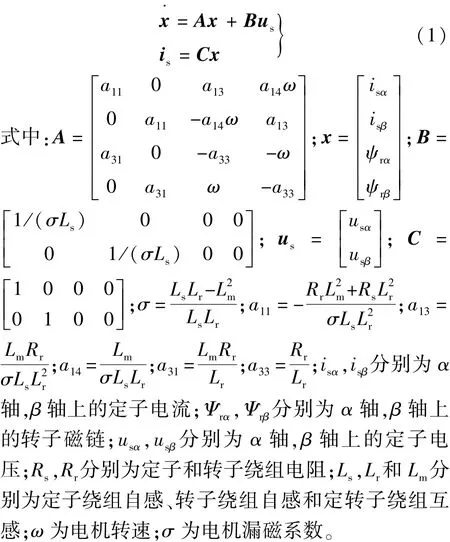
2 滑模磁鏈觀測器及速度估計器設計
2.1 滑模磁鏈觀測器設計及穩定性分析
分離矩陣A中的轉速,將式(1)改寫成如下形式:
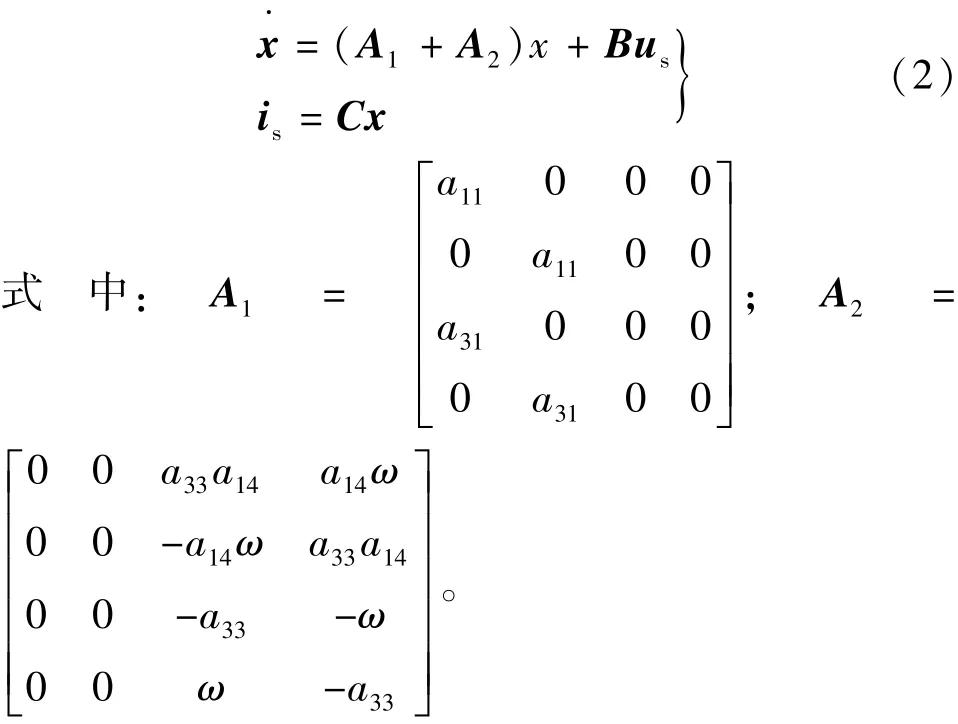
根據式(2)構造滑模變結構磁鏈觀測器:
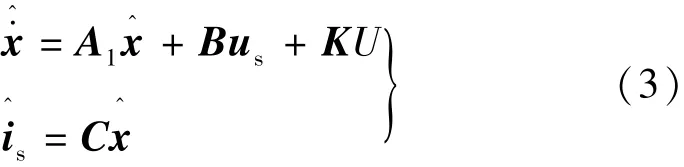
式中:“^”為估計值;U為滑模控制函數;K為系數矩陣,
從式(3)可以看出,該觀測器中不含轉速信息,系數矩陣都為定值,結構簡單。下面進一步驗證觀測器的穩定性。
式(2)減去式(1)得:
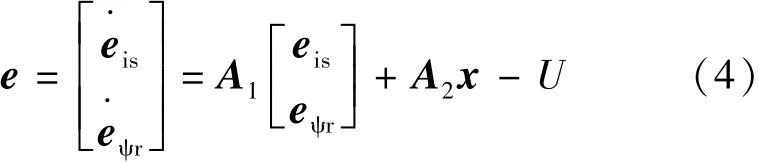
式中:eis,eΨr分別為電流誤差和磁鏈誤差,
構造李雅普諾夫函數[9]:
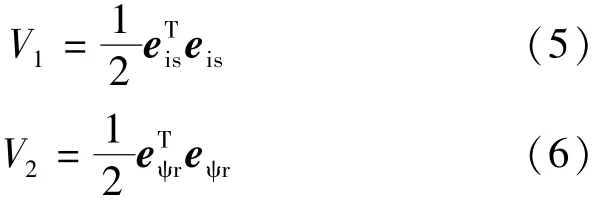
很容易看出式(5)、式(6)非負,對它們求導可得:

將式(4)分別代入式(7)可得:
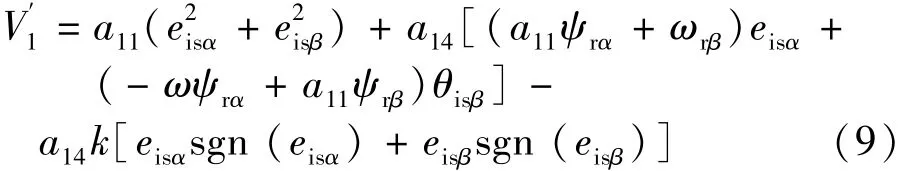
由于 eisαsgn(eisα)+eisβsgn(eisβ) >0,所以當 k 足夠大時,,根據李雅普諾夫穩定性原理可得,系統漸進穩定。即電流估計值趨近于實際值。根據等效控制原理[10],由式(4)可得:
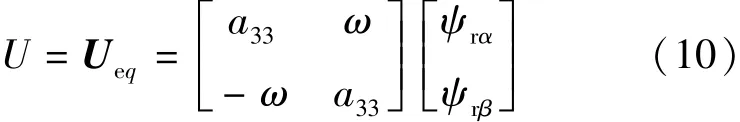
將式(4)、式(10)代入式(6)可得=0,所以磁鏈誤差也是收斂的,即磁鏈觀測是準確的。
2.2 減少抖振的措施
滑模觀測器由于存在慣性,系統會在希望估計之間振蕩,出現抖振現象[11]。為了減少抖振,本文采用飽和函數式(11)進行連續化處理(η為很小的正常數)[12],同時采用式(12)進行低通濾波處理(τ為濾波時間常數)[13]。
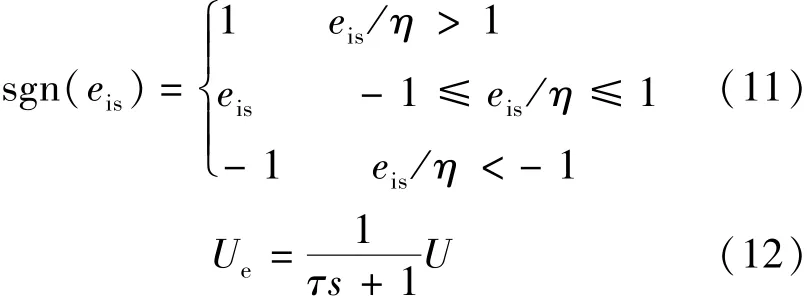
2.3 轉速估計器設計
根據式(10)可得:
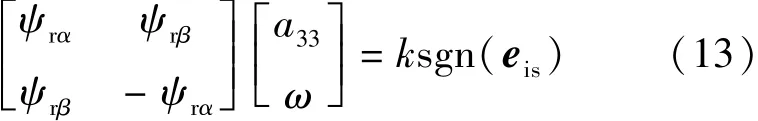
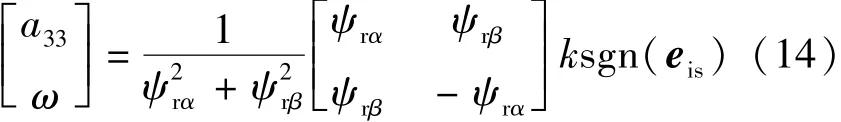
由式(14)可得估計轉速:
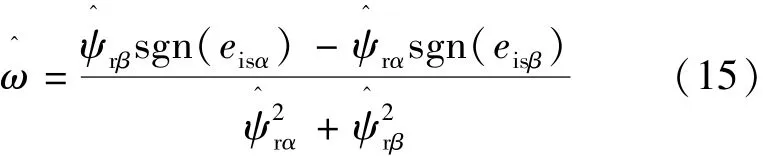
基于滑模磁鏈觀測器的速度估計器模型如圖1所示。
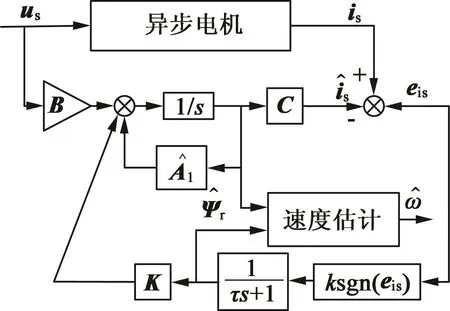
圖1 基于磁鏈觀測器的速度估計器模型
3 容錯控制策略
速度傳感器故障時,基于速度估計器的電機系統容錯控制策略如圖2所示。采用閾值故障診斷法,根據所需精度要求選擇一個殘差閾值。當速度傳感器故障時,傳感器輸出信號與速度估計值之間殘差將會突變,當殘差超出閾值時,判定傳感器故障。此時將傳感器隔離,將速度估計器的輸出作為新的反饋,系統切換為不依賴于速度傳感器的無速度傳感器矢量控制,保證系統的連續運行,從而實現對電機系統的容錯控制。
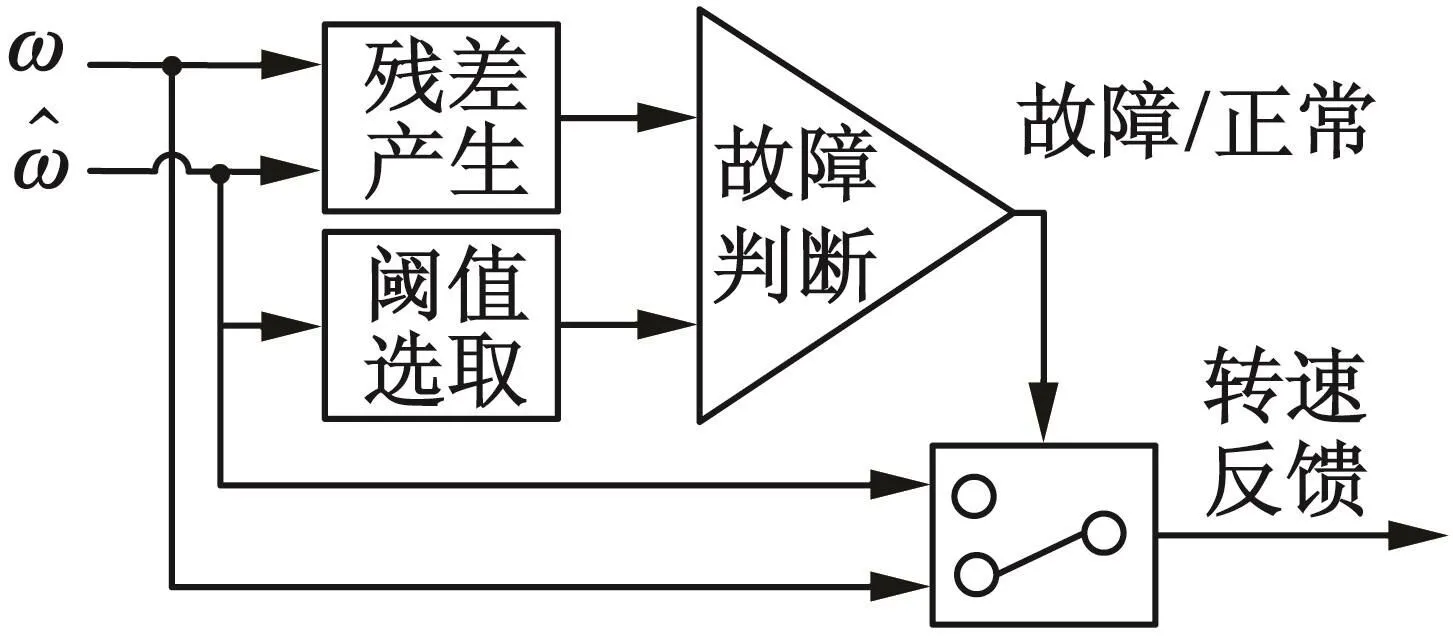
圖2 電機系統容錯控制策略框圖
4 仿真及實驗驗證
為了驗證上述方法,進行MATLAB仿真。電機系統采用轉差型間接矢量控制。系統原理圖如圖3所示。速度傳感器的信號沒有直接反饋給控制回路,而是經過容錯控制環節的狀態監測。根據傳感器的狀態選取反饋信號。電機參數:額定功率22 kW,額定線電壓220 V,額定頻率50 Hz,Rs=0.3Ω,Rr=0.25Ω,Ls=Lr=0.041 2 H,Lm=0.040 3 H。 空載起動,在0.8 s時加負載TL=60 N·m。
圖4、圖5為采取減少抖振措施的切換函數和未采取措施的切換函數。圖6、圖7為α軸轉子磁鏈、定子電流的觀測值和實際值。圖8為轉速的觀測值和實際值以及誤差。從圖4~圖8中可知,采取上述減小抖振的方法后,切換函數的振蕩現象明顯改善;轉子磁鏈、定子電流以及轉速的觀測值精度較高。
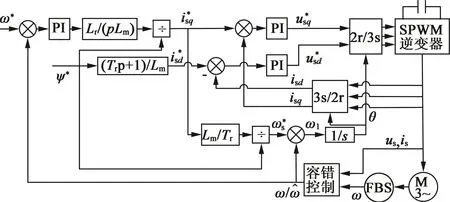
圖3 電機系統容錯控制框圖
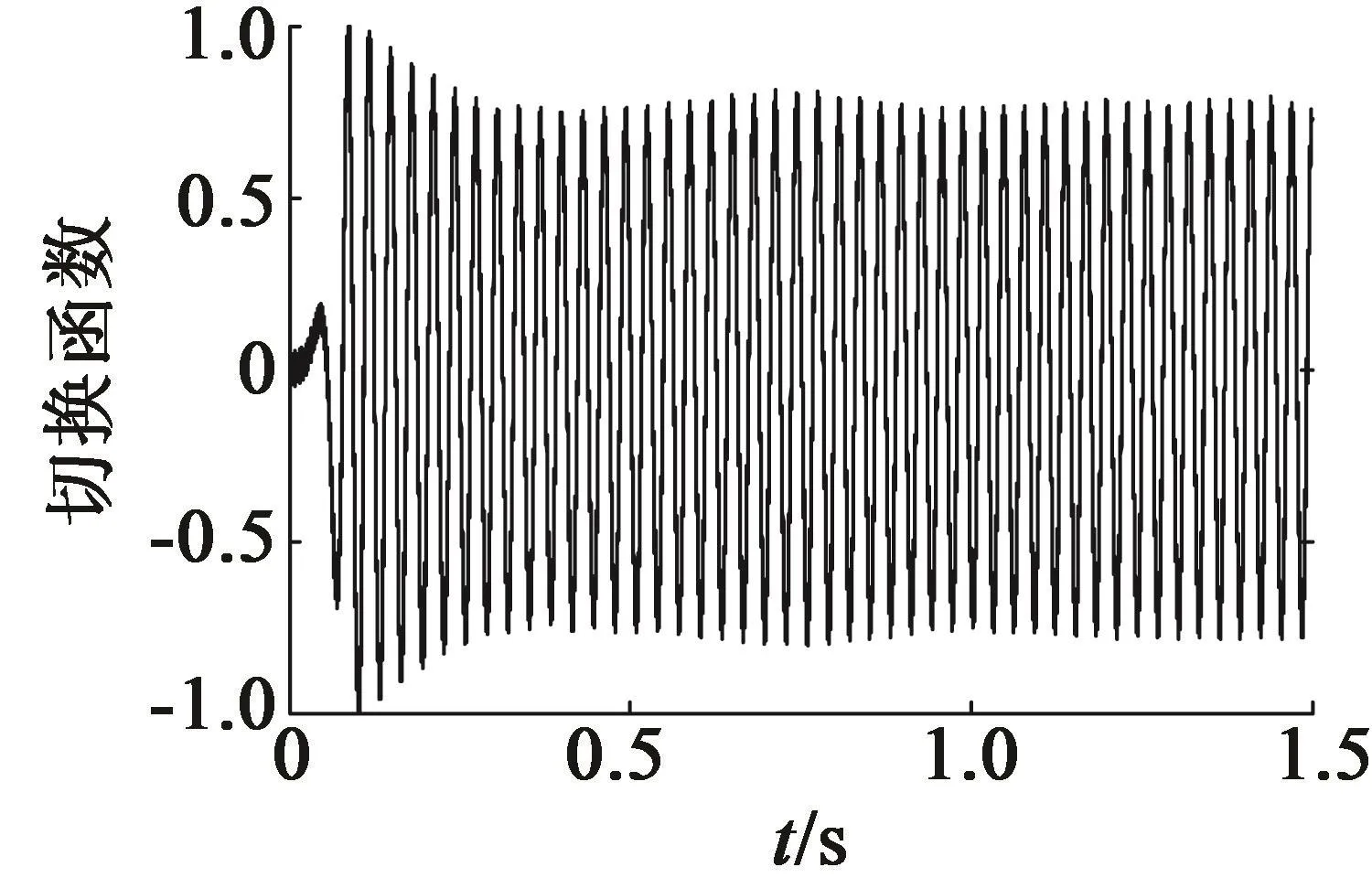
圖4 采取減少抖振措施的切換函數
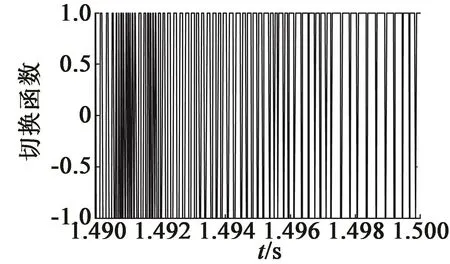
圖5 未采取減少抖振措施的切換函數
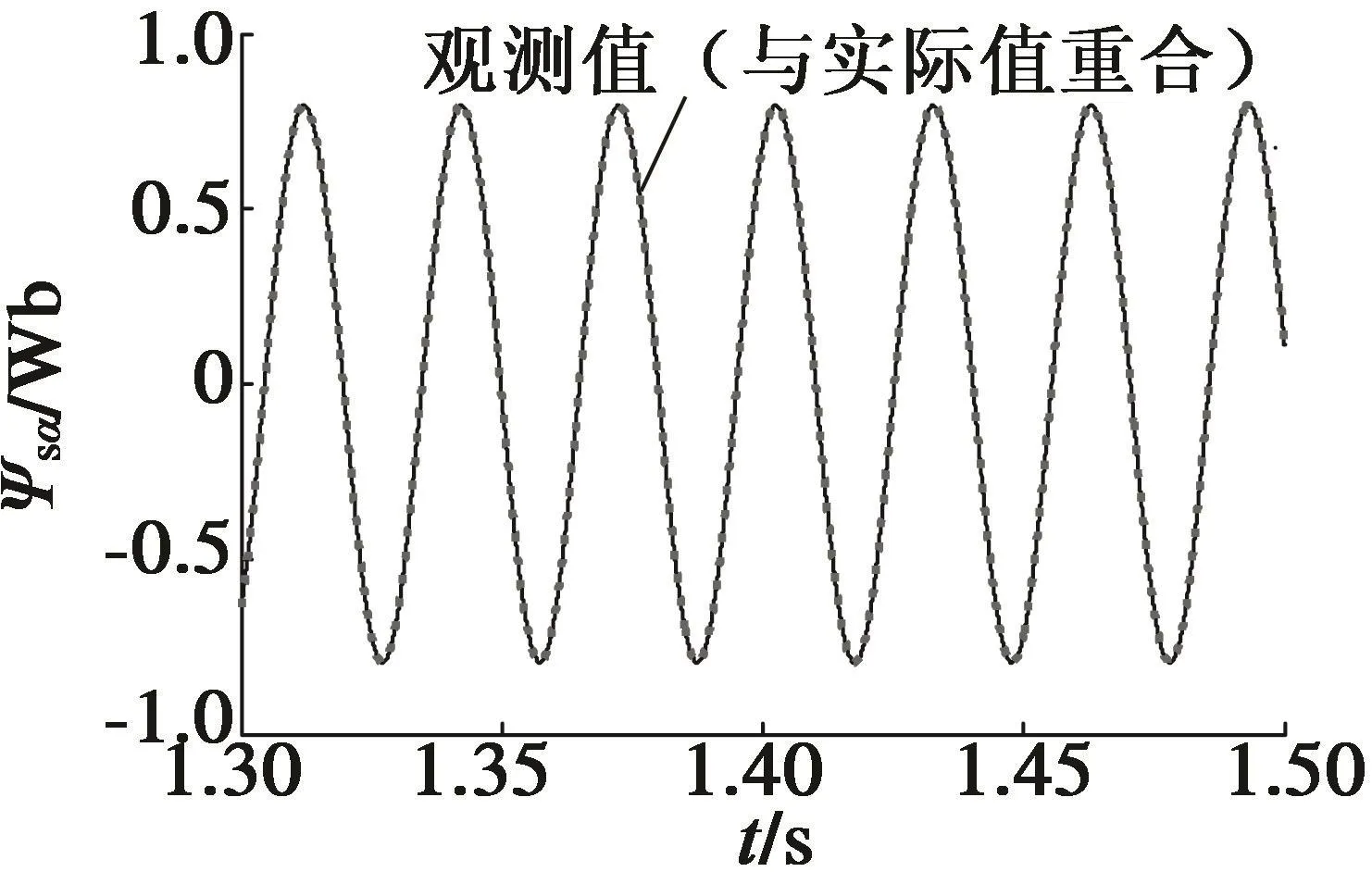
圖6 轉子磁鏈觀測值和實際值
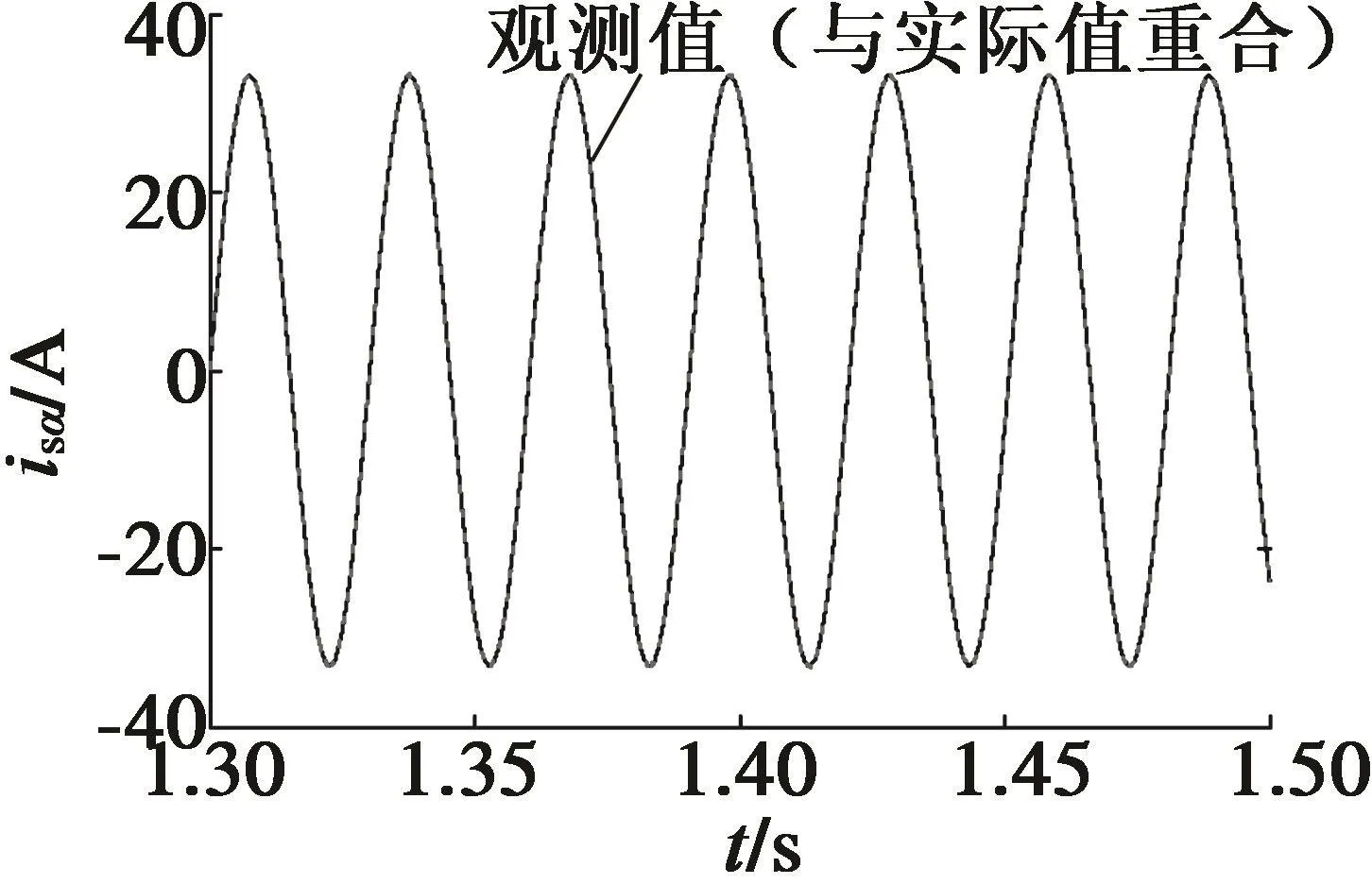
圖7 定子電流觀測值和實際值
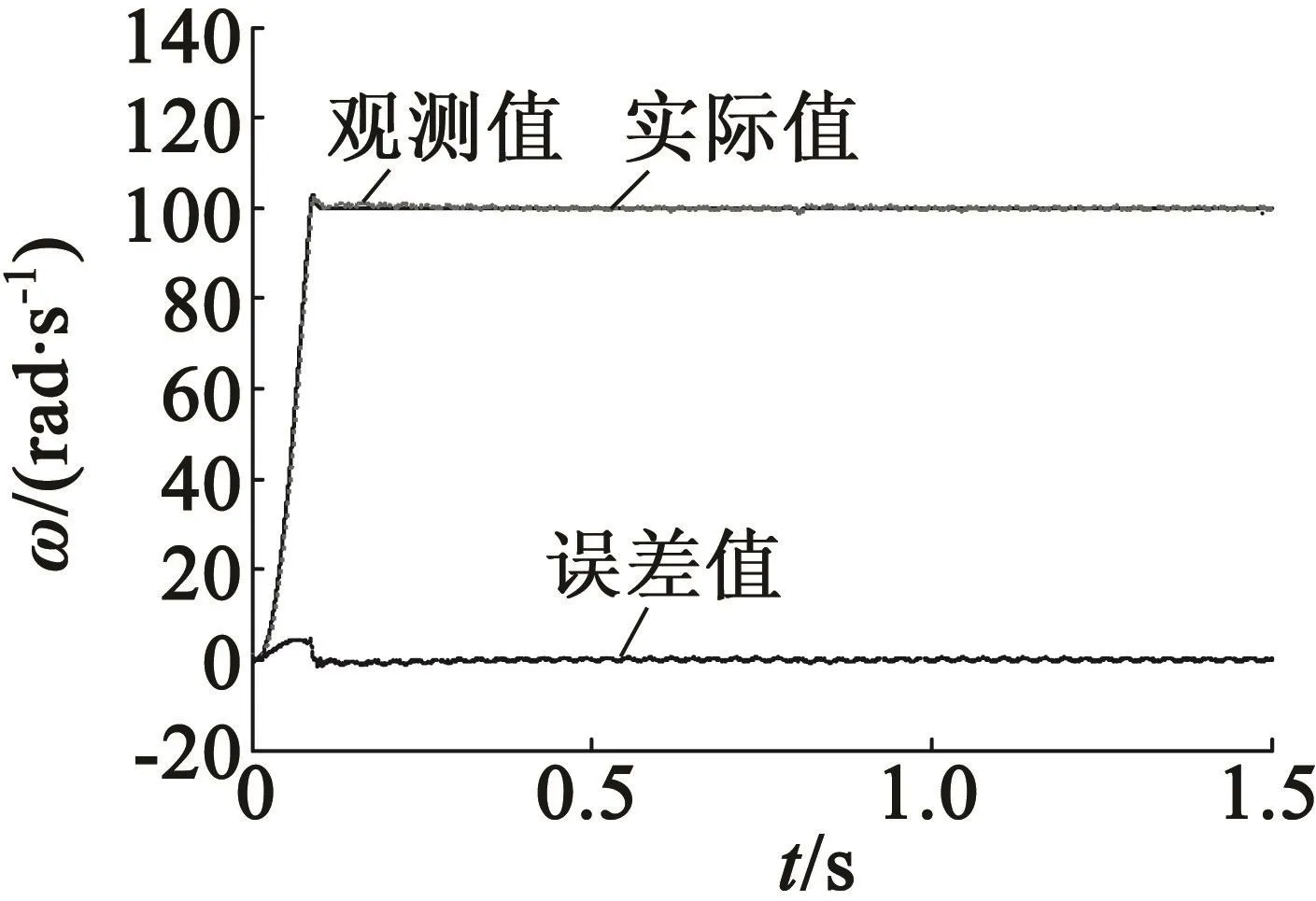
圖8 轉速的觀測值、實際值和誤差值
傳感器故障大體可以分為3類:斷路故障、固定偏差故障以及漂移故障。這里選擇斷路故障和固定偏差故障進行驗證。
情況1:斷路故障,在1 s時傳感器失效,出現斷路故障,輸出值為零;
情況2:固定偏差故障,在1 s時傳感器輸出值發生固定偏移。取閾值為5 rad/s。圖9、圖10為兩種類型傳感器故障下的轉速情況。
從圖9可知,當傳感器在1 s出現斷路故障時,偏差值突變,超出設定的閾值,判定傳感器故障,此時將觀測轉速作為系統反饋,保證電機系統的連續運行,從而實現對傳感器故障的容錯控制。從圖10可知,當傳感器出現固定偏差故障時,同樣可以完成診斷,保障系統的連續運行。
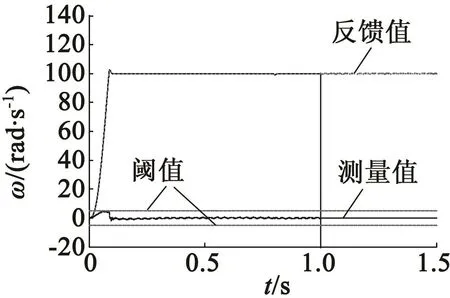
圖9 情況1下的轉速波形
基于dSPACE DS1007搭建實驗平臺進行驗證,開關頻率為1 kHz,結構圖如圖11所示。包括變頻器、電機、增量編碼器、dSAPCE和驅動器等。主要用到的板卡包括DS5202(FPGA基板)和DS5202 ACMC(AC Motor Control)(編號為EV1048)。DS5202負責給編碼器供電,EV1048負責編碼器信號的采集和AD采樣,以及PWM輸出。在3 s時給定傳感器故障。圖12是α軸定子電流的觀測值和實際值,圖13是α軸轉子磁鏈的觀測值與實際值,圖14是給故障情況下傳感器的測量值和系統反饋轉速。實驗進一步驗證了該容錯策略的有效性。
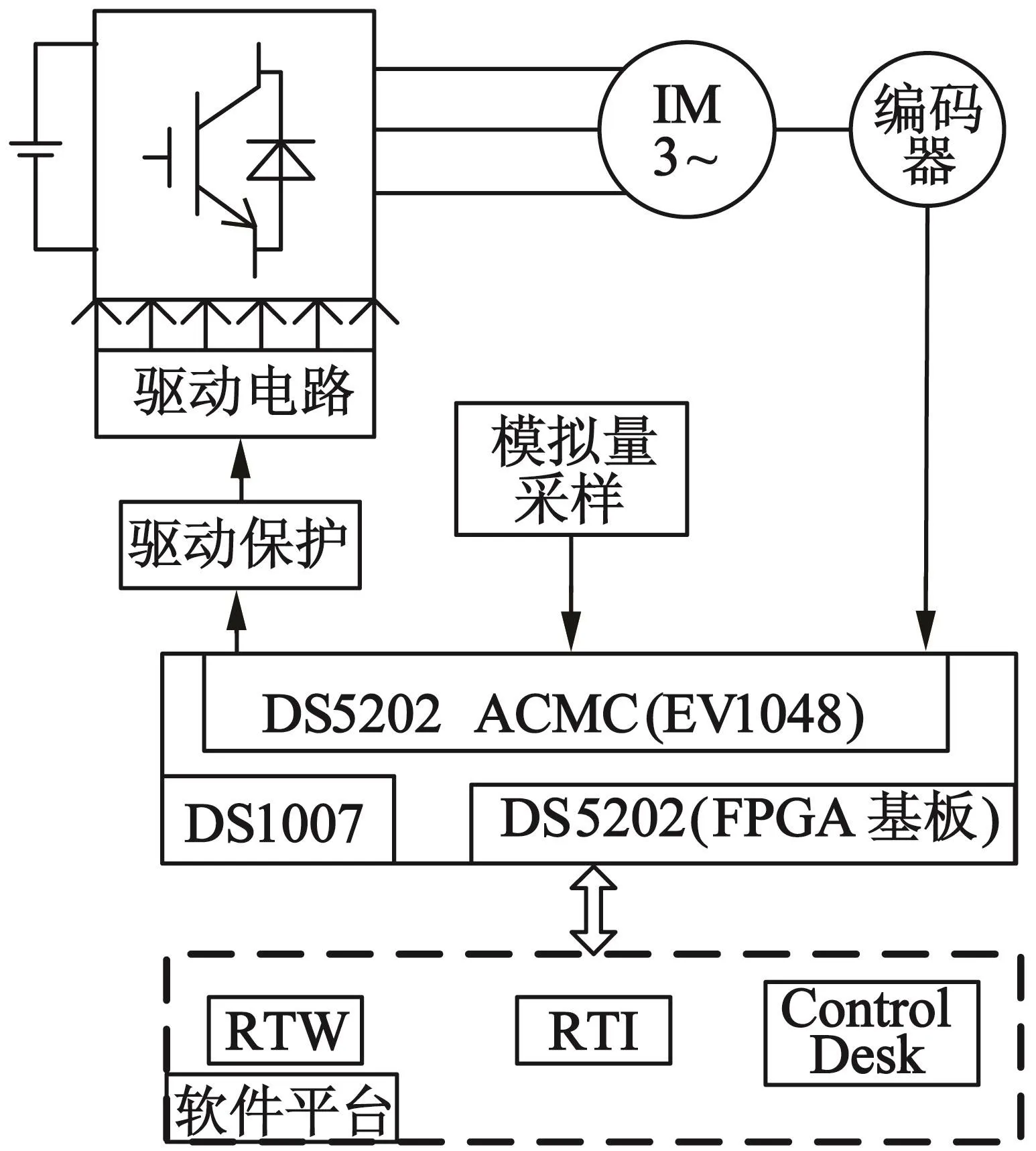
圖11 實驗平臺結構圖
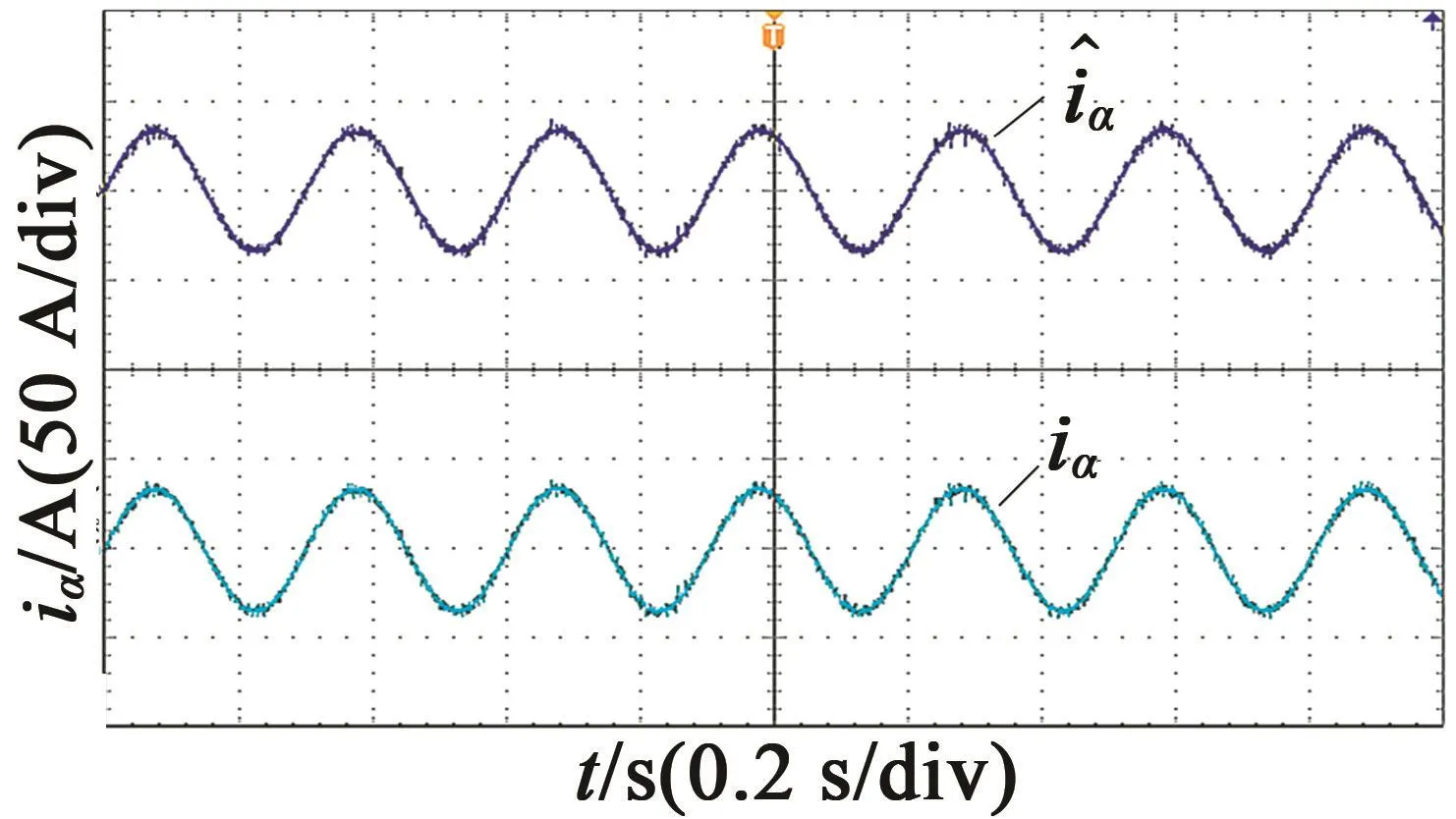
圖12 定子電流觀測值和實際值
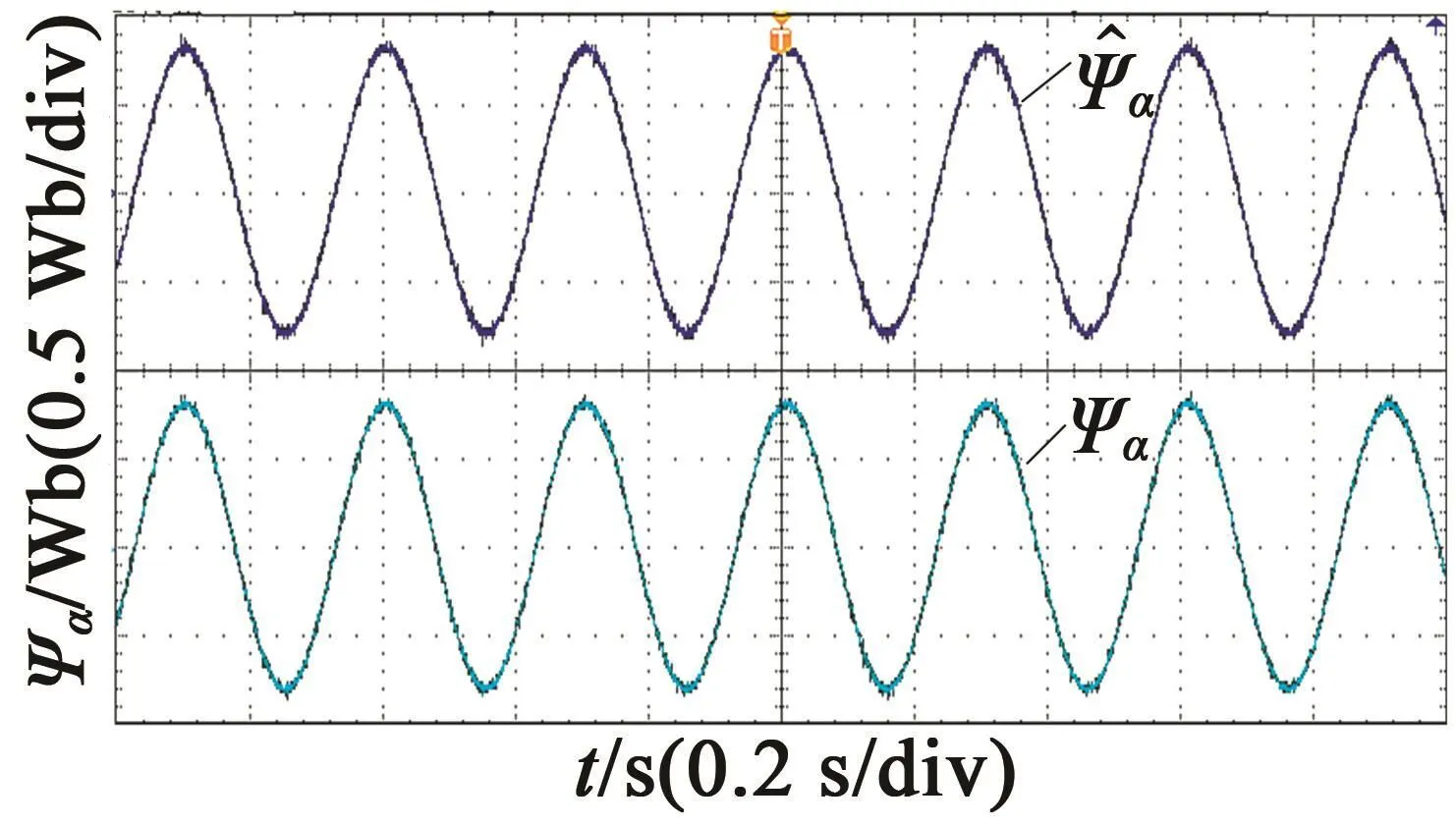
圖13 轉子磁鏈觀測值和實際值
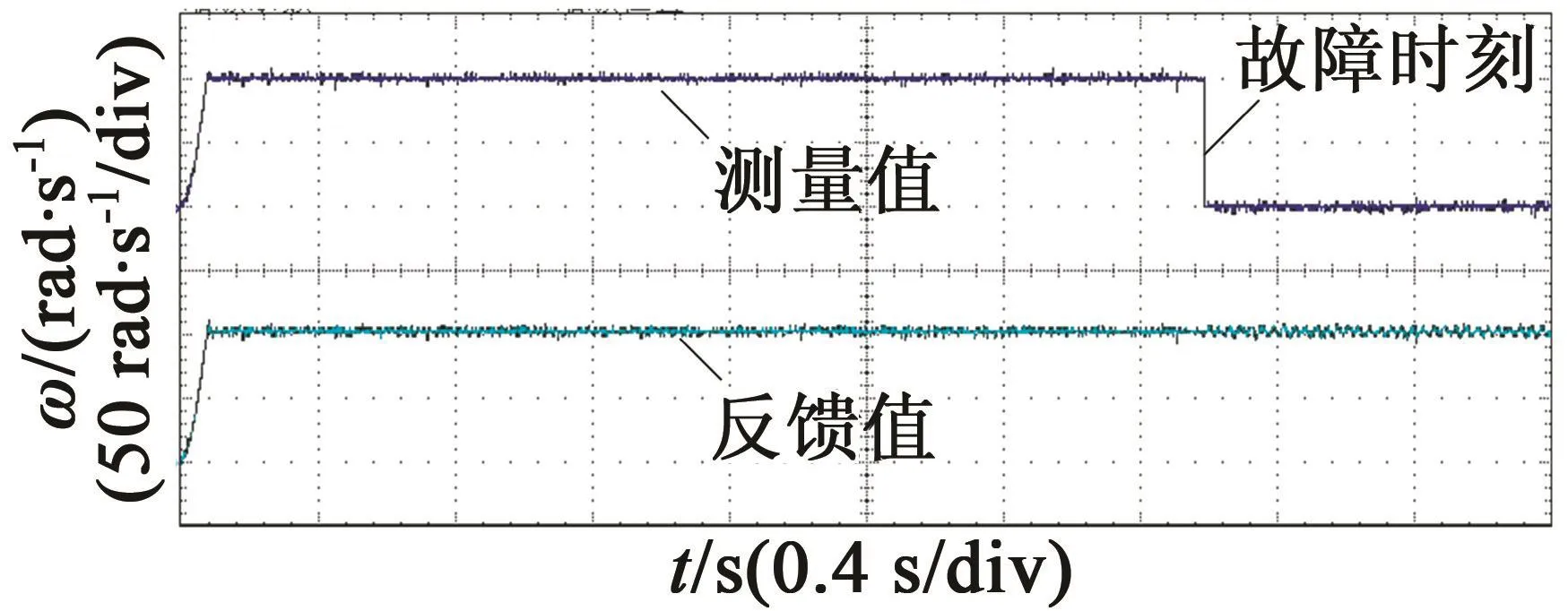
圖14 故障情況下的測量值和反饋值
5 結 語
本文針對感應電機控制系統中速度傳感器故障,基于滑模變結構觀測器提出了一種容錯控制策略。該觀測器不需要轉速輸入,觀測性能良好,魯棒性強。利用該觀測器設計速度估計器,通過速度估計器進行故障診斷,當速度傳感器出現故障時,可以診斷出故障,利用估計轉速作為系統反饋,系統切換為無速度傳感器矢量控制,保證系統連續運行,從而實現對傳感器故障的容錯控制。仿真驗證了該容錯控制策略的有效性。

