無傳感器永磁同步電機模型參考模糊自適應系統

趙換麗,王 艷,許允之

(1.平頂山學院,河南467000;2.中國礦業大學,徐州221116)

0 引 言

永磁同步電機因高效、高功率密度、高轉矩密度及高可靠性而被廣泛使用。但使用傳感器的電機增加了系統的復雜性并降低了整體系統的可靠性,因此永磁同步電機的無傳感器控制方法受到普遍關注并進行了廣泛研究。

模型參考自適應算法是一種易于數字化的電機轉速和位置觀測算法,在各類參數辨識中均獲得了良好的應用[1-2]。然而此系統的缺點在于依賴于觀測器的準確度,尤其是當電壓模型受到定子電阻值影響而產生變化時。采用定子電阻觀測器可以補償以上弊端,但是同時進行多參數辨識明顯降低了系統的響應速度[3]。

為了從本質上解決模型參考自適應系統對參數的敏感性問題,諸多文獻提出將不依賴參數的模糊邏輯或滑模算法融入其中[4-6]。為了提高含有滑模控制的MRAS系統的精度和穩定性,設計二階滑模結構的復雜度較高[4]。相比之下模糊系統結構較為簡單,且執行效率更高。文獻[5]將系統多個狀態輸入單一的模糊控制器,共設計了7個邏輯子集,模糊蘊涵關系過于復雜,隸屬度函數校驗成功率較低。

鑒于系統缺陷和已有的研究經驗,本文將模型參考自適應結構中傳統的PI調節器替換為非線性模糊邏輯單元,提出基于模型參考自適應的兩級式模糊邏輯系統結構。兩級式結構有效地降低了參數間的耦合性,同時提高了轉速跟蹤性能,并在不同的工況下提供優異的自適應能力將轉速誤差降到最小。

1 模型參考自適應系統機理分析

使用模型參考自適應算法的目的是為了更加精確的觀測定子d,q軸的電流和電機轉速。模型參考自適應系統從結構上包括參考模型和可調模型。參考模型的作用是用以確定已知的定量值,可調模型作為一個自適應模型可根據不同給定值產生相應的期望輸出結果。再將參考模型的輸出和可調模型進行比較,并將兩者輸出誤差信號送入自適應機中,獲得估算的電機轉速反饋至可調模型中。常規的模型參考自適應算法估算轉速的結構框圖如圖1所示。

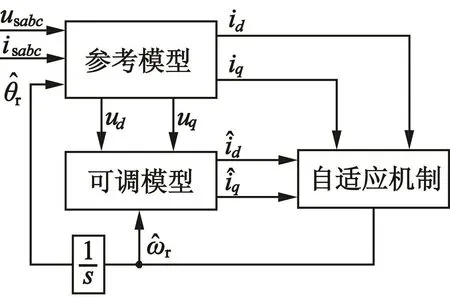
圖1 模型參考自適應系統結構框圖

設d-q坐標系為永磁同步電機中的同步旋轉坐標系,則電機在此旋轉坐標系下的數學模型:

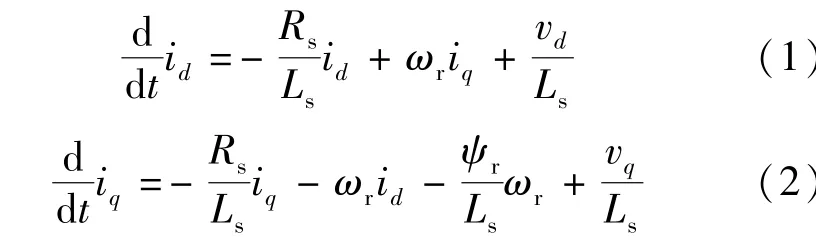
式中:vd和vq分別表示d軸和q軸的定子電壓分量;Ls和Rs為定子電感值和電阻值;ωr為轉速;ψr為轉子磁鏈。將以上電流方程寫為矩陣形式:

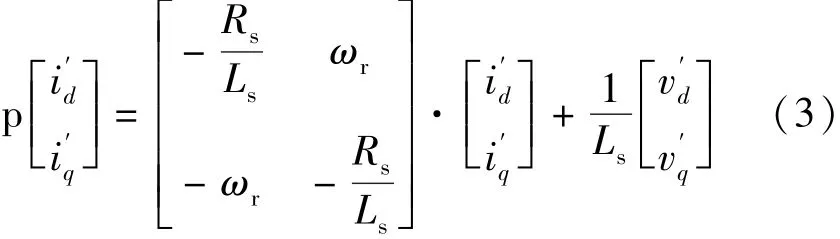
式中:

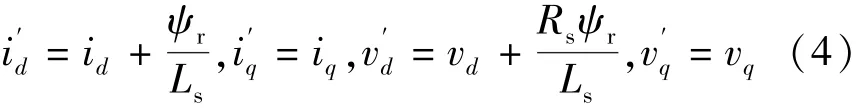
式(3)中存在時變量ωr,因此作為可調模型。永磁同步電機作為參考模型,并產生id和iq兩個參考值。則根據以上關系可設計出基于常規PI的模型參考自適應控制系統。對式(3)進一步簡寫可得:

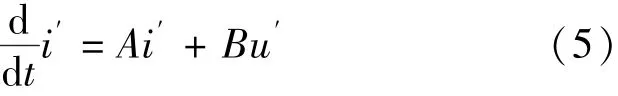
因此可調模型的數學方程如下:

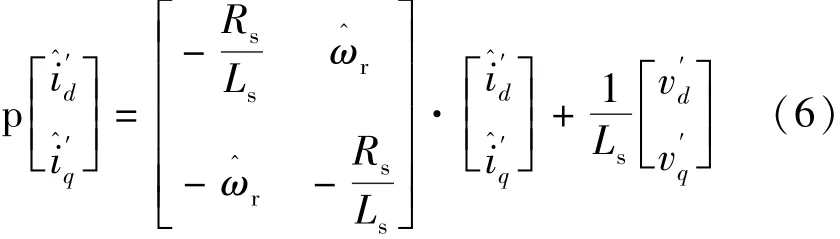
同理,式(6)可以簡寫:

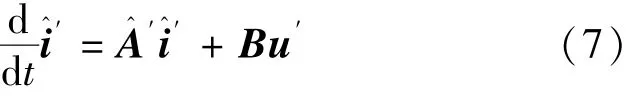
在此模型中,ωr是需要觀測的量,其它參數均為定值。則電流誤差:

結合波波夫穩定性系統判據,則串聯模型的數學表達式:

式中:

依據波波夫超穩定性理論,如果系統滿足:

1)狀態矩陣H(s)=D(sI-A)-1嚴格為正實數;2)波波夫積分不等式

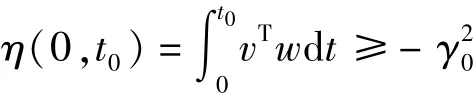
對于?t0≥0,是一個與t0相關的有限正常數。

滿足以上條件,則設計的模糊模型參考自適應系統滿足漸進穩定性。若系統繼續滿足tl→im∞e(t)=0,則基于此MARS的系統是絕對穩定系統。

因此,結合以上分析可推導出估算算法的數學模型如下:

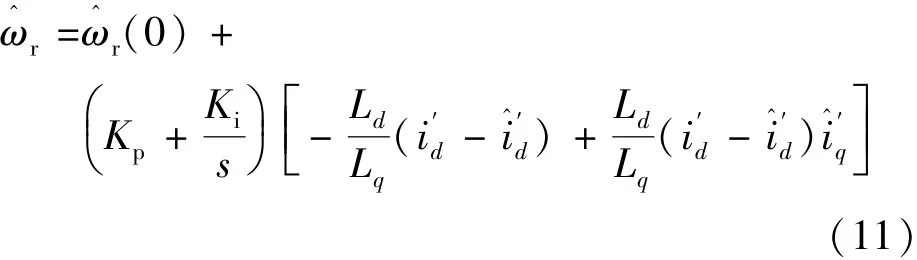
將式(4)代入式(11)時可得:

動漫旅游的核心競爭力是動漫游藝作品帶給觀眾的體驗和心靈的感受，動漫在旅游中能夠讓人們找到與動漫人物的共鳴，進行深度的體驗，因此動漫IP在整個動漫旅游中為最重要的一環，如何打造一個成功的動漫IP，才是第一步要做的。打造動漫IP有幾種形式：

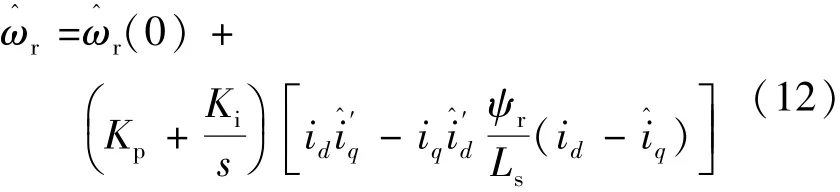
式中:通過可調模型計算獲得;id,iq通過參考模型獲得。所采用的為混合自適應律方法,此算法在高度非線性系統建模分析中具有明顯優勢,應用到模型參考自適應亦可獲得良好性能。

2 模型參考模糊自適應系統設計

傳統模型參考自適應系統的結構系統如圖1所示,系統中的永磁磁鏈和電感值受系統運行狀態和實際參數影響較大。為了減弱甚至消除原系統中對于永磁磁鏈和電感的依賴性,引入模糊控制系統結構并演化出圖2的結構框圖,因此,含模糊系統的新結構系統響應大幅提高,穩態誤差大幅降低。

圖2 兩種系統自適應結構框圖對比

模糊系統對實際系統和控制對象的數學模型無依賴性,對系統狀態的自適應性能更好,尤其在非線性系統中應用廣泛[7-8]。

使用模糊控制的本質是為了減少迭代計算的次數以降低處理器的計算耗時。在常規的模糊邏輯系統中,所涉及的規則總數急劇增長,當采用多級串聯結構時,可調節控制規則增長方式為線性。

所提結構包括兩個模糊系統單元,對系統參數進行相關度分析,將相關度高的系統變量從第一層結構中輸入,相關度低的變量從第二層結構中輸入。實際上,在此結構中每個雙輸入模糊邏輯控制器均引入了輔助增益系數以輔助調節系統性能,采用雙輸入結構相比常規的單輸入模糊控制器規則更加精簡,同時此結構下的模糊規則數量也可以因此而減少[5]。

本算法將3個變量(e1+Δe1+Δe2)作為輸入進行計算。模糊系統的元素規則表如表1所示。分別有正(P)、負(N)、零(Z)3種狀態。本文中,所提出的結構采用兩級模糊子系統,每個子系統僅含有兩個輸入信號。第一個子系統的輸入信號為e1和Δe1,輸出為Δu1,并結合Δe2作為第二級子系統的輸入,如圖3所示。

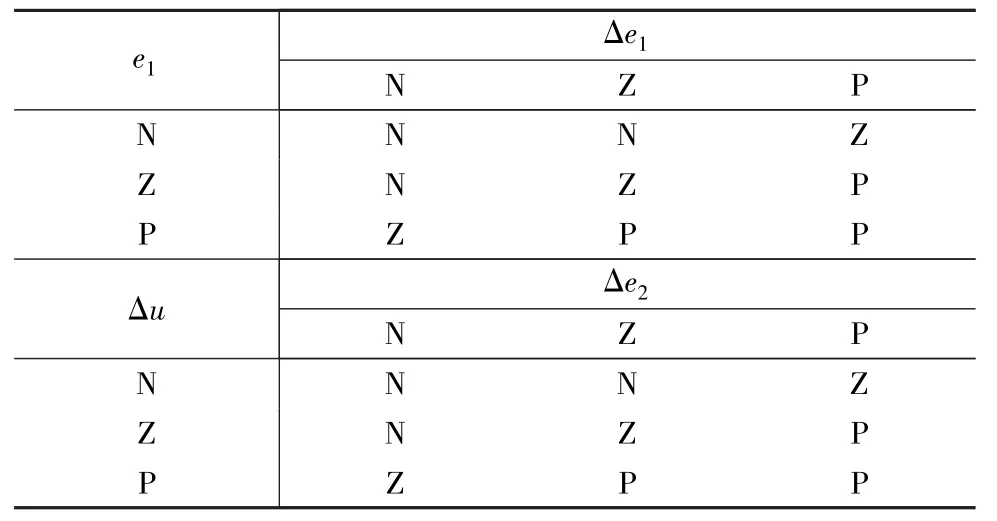
表1 子系統的模糊邏輯規則表

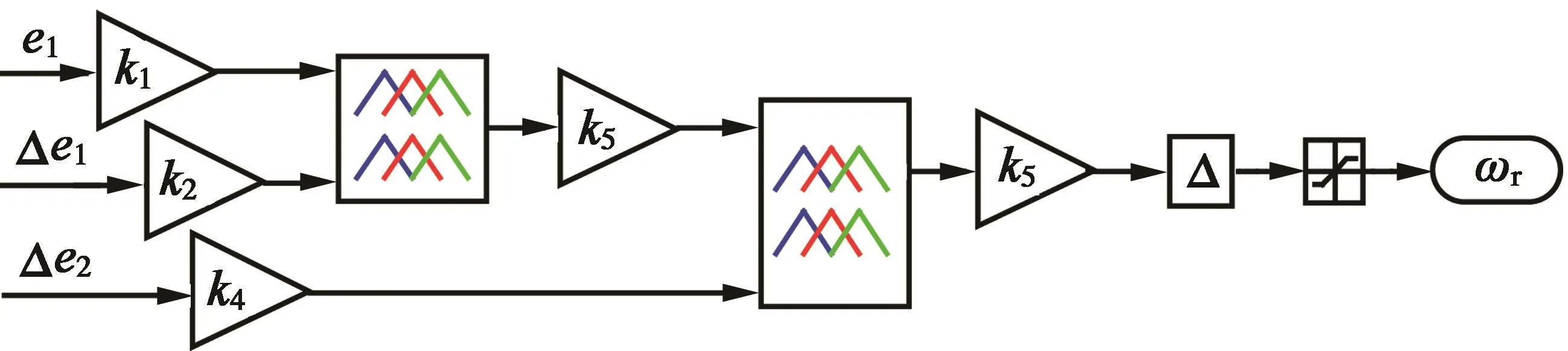
圖3 兩級模糊系統結構示意圖

模糊系統中的誤差變量e1和e2的定義如式(13)、式(14)所示,Δe1和 Δe2分別為其對應的增量。在本模糊系統中,第一個輸入信號為e1;第二個輸入信號為Δe1,此信號與e1的變化速度相關;第三個輸入信號為Δe2,此值由e2的增量信號獲得。

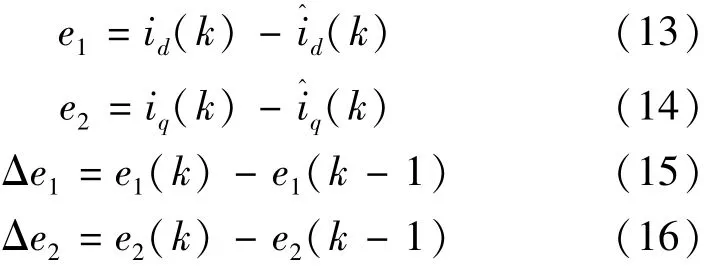
圖3中的k1～k5為輸入輸出信號的輔助增益系數,具體取值可根據相應的應用場景進行調整以改善系統的性能。本文中各項增益的具體取值為k1=k2=k3=k4=1,k5=0.1。

采用三角形隸屬函數定義如圖3所示的兩組模糊系統。本研究采用Mamdani模糊邏輯推理類型和質心解模糊化方法輔助調整模糊子系統的隸屬度函數。

因本系統采用雙層串聯型模糊控制單元,第一層單元中的參數對系統狀態的影響權重較高,因此其隸屬度函數設計較為嚴苛。結合表1的控制規則,第一層模糊子系統的錄屬度函數如圖4所示。

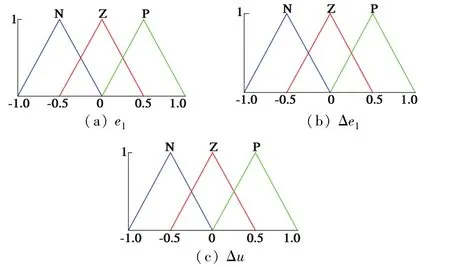
圖4 第一層模糊子系統的錄屬度函數

3 實驗分析

在實驗分析中,DC直流電壓輸入為311 V,逆變器采用SVPWM控制方式,開關頻率為10 kHz,通過電流及電壓傳感器將信號采集并AD轉換后輸入DSP芯片進行計算處理。實驗所采用的控制拓撲結構如圖5所示,電機主要參數如表2所示。

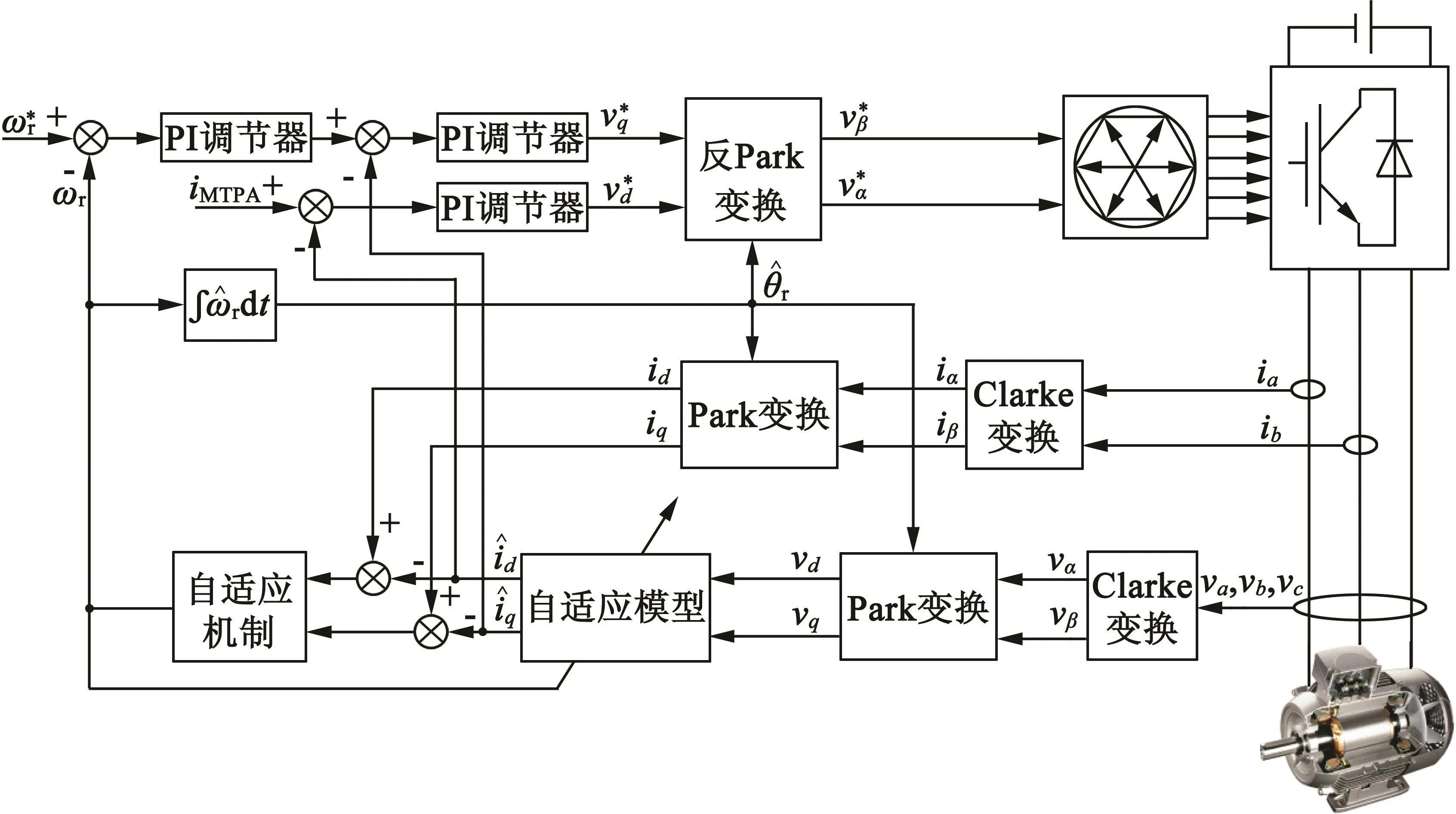
圖5 采用MARS的永磁同步電機矢量控制系統結構框圖

表2 實驗電機的額定參數

3.1 動態性能對比

為了對比分析模型參考模糊自適應控制算法與采用PI調節的傳統模糊控制算法的具體動態性能,設計實驗分析研究了電機低速和高速域的運行情況,具體如下:

工況1:電機初始狀態靜止,在0.2 s時將給定轉速由0突變到100 r/min,并在1 s時將給定轉速由100 r/min突變為反向100 r/min。

工況2:電機初始狀態靜止,在0.2 s時將給定轉速由0突變到1 000 r/min,并在1 s時將給定轉速由1 000 r/min突變為反向1 000 r/min。

在工況1和工況2下采用兩種不同算法的轉速實驗波形分別如圖6和圖7所示。由圖6、圖7可知,模型參考自適應控制性能較弱的低速區域下,引入模糊結構單元后電機在動態響應速度有明顯的提升,耗時僅為傳統算法的30%左右。高速區域下常規算法性能良好,但是模糊算法對轉速的跟蹤速度依然更快,約節約時間40%。此外,不同于PI完全依賴于誤差輸入的調節方式,模糊控制算法在穩態狀態下紋波相對較低,調整時間較短,轉速誤差幾乎為0。

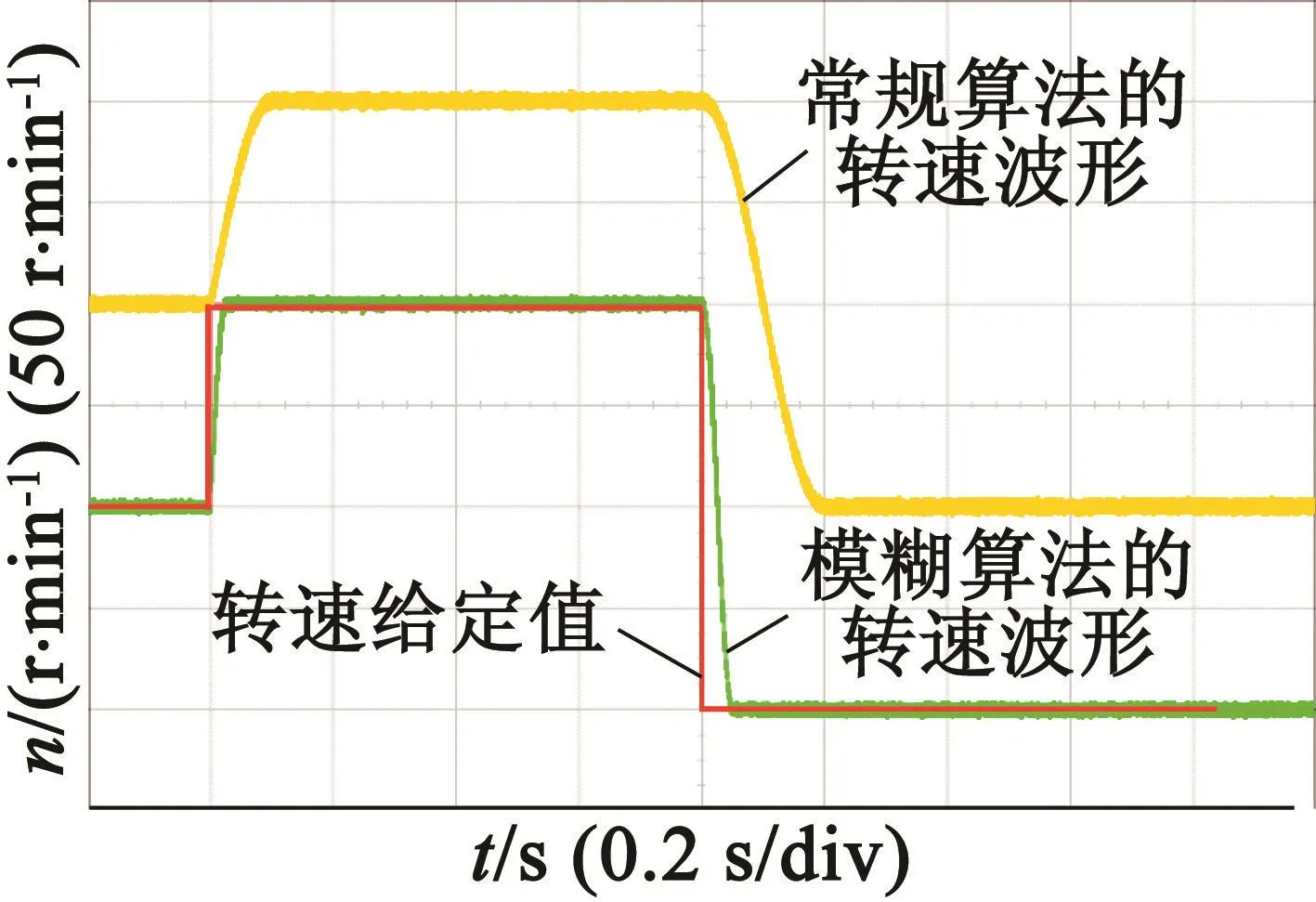
圖6 低速工況下兩種控制算法的轉速實驗波形

圖7 高速工況下兩種控制算法的轉速實驗波形

模型參考自適應算法在電機高速運行時的轉子位置檢測效果良好,而低速時一般精度較低。在工況1下運行時兩種算法的角度估算結果如圖8所示。由圖8可知,模糊模型參考自適應算法下電機的定位精度更高且定位速度更快,它在低速下的定位精度提高約57%。

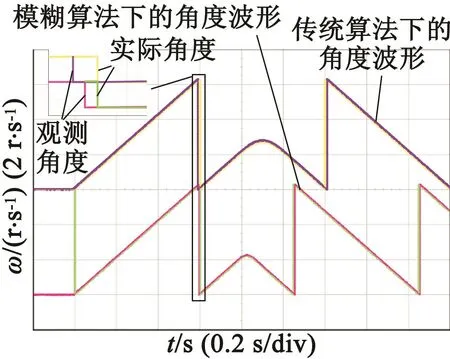
圖8 低速工況下兩種控制算法的位置估算結果

3.2 穩態性能對比

為了分析電機穩態運行全指標的詳細性能,實驗分析了低速、中速和高速下兩種算法的不同指標結果,具體對比如圖9所示。圖9中縱坐標為相同工況下兩種算法的實驗結果值總和,橫坐標為不同轉速工況以及所對應的性能指標。

圖9分別實驗分析了100r/min,500r/min和1 000 r/min轉速情況下兩種算法的實際性能。

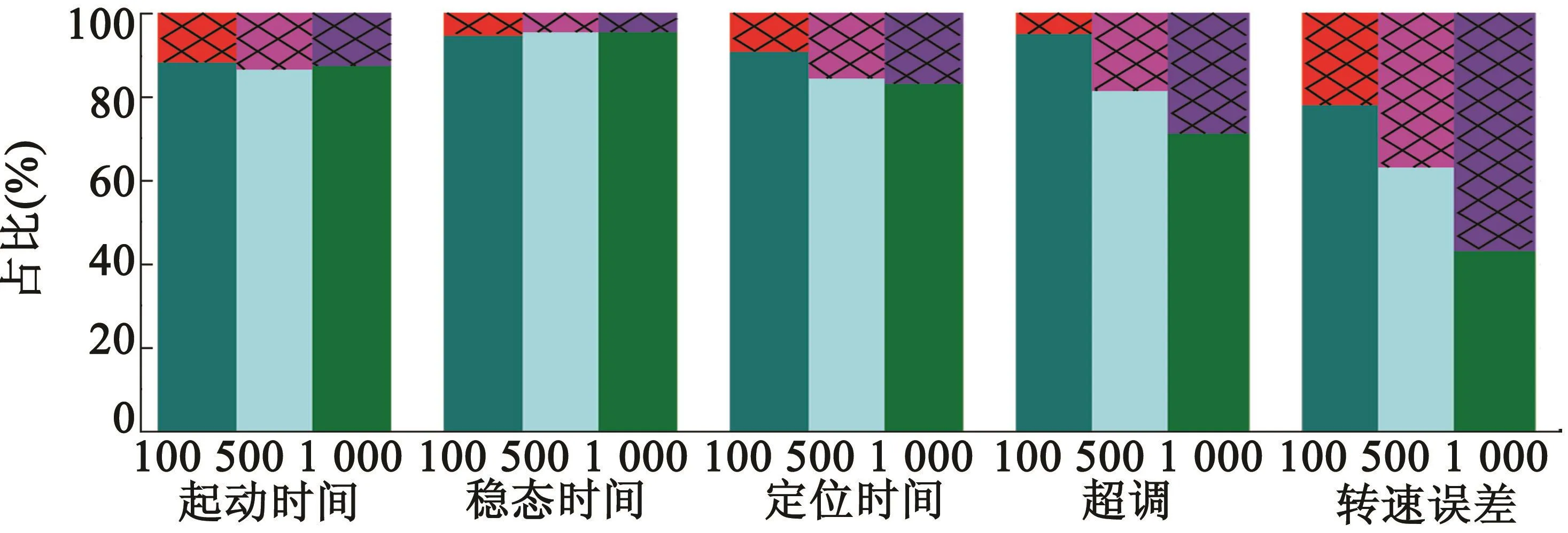
圖9 兩種方法不同轉速下各項穩態性能指標對比

圖9 中含網格底紋的柱形圖表示模糊算法下的實驗結果,其下方為傳統算法的實驗結果。由圖9可知,在不同轉速下,新算法的起動時間、穩態調整時間、轉子定位時間、超調量均明顯小于傳統算法,且優化效果有絕對優勢。而低速時的轉速誤差也有明顯降低,在高速域轉速誤差與傳統算法相當。

4 結 語

本文研究并提出了一種針對永磁同步電機的模型參考模糊自適應無傳感器控制系統,并將所提出的方法與傳統的PI調節器進行對比分析。實驗結果表明,采用兩級式模糊系統可以有效降低系統的復雜度,從而提升系統的動穩態性能。與傳統算法相比,模糊算法彌補了低速域下轉速脈動大、轉速跟蹤慢等缺點,在全速域下平均電機性能提升50%以上。而相比于PI系統,所提方法復雜度無明顯提升,適合數字控制系統的推廣應用。