結合滑模控制和反饋線性化的感應電機控制
羅 樂
(成都工業學院,成都611730)
0 引 言
相對于感應電機的矢量控制策略,直接轉矩控制(以下簡稱DTC)具有較高的魯棒性,且具有更快的響應速度[1-3]。傳統的DTC控制器使用滯環轉矩和磁鏈控制并結合開關表選擇電壓矢量作用到電機,從而避免使用了電流閉環,提高了響應速度。但DTC控制器容易造成較大的轉矩脈動,這將造成噪聲,增加額外的損耗,降低電機生命周期,同時魯棒性也較低[4-5]。針對這個問題,文獻[6]基于現代控制理論,采用離散空間矢量控制技術,提出了改進型的恒定開關頻率DTC方案以減小轉矩脈動。文獻[7]提出了基于線性轉矩和磁鏈控制的DTC方案,文獻[8]提出了一種變結構的DTC控制方案。
反饋線性化是一種非線性控制方法。其主要思路是利用非線性反饋環節將一個非線性系統轉換為一個等效的線性系統,然后可以使用傳統的線性方法設計控制器[9]。但是由于反饋線性化方法對模型誤差和擾動較為敏感,文獻[10-12]分別使用了基于轉速、電流或磁鏈對電機模型進行了反饋線性化設計,文獻[13-16]對變頻器模型進行反饋線性化設計。其中文獻[16]對反饋線性化模型的誤差敏感度進行了分析,顯示由于擾動、參數偏移或傳感器誤差都有可能降低控制性能。滑模控制(以下簡稱SMC)是一種針對系統不確定性和模型誤差的魯棒控制方法[9],它已成功地應用于感應電機驅動器,并在較寬的轉速范圍提供了較好的動態性能[17-22]。
本文在上述文獻研究基礎上,設計了一種結合滑模控制和反饋線性化的新型改進DTC控制方案,用于感應電機驅動。由于采用了反饋線性化方法,該方案具有可以使用經典控制理論設計控制器的優勢,即可以對魯棒性和穩定性進行分析。此外,觀測器和控制分離的原則使得兩者可以獨立設計[23]。將反饋線性化結合滑模控制可以克服反饋線性化方法對擾動和不確定敏感的問題。本文通過將狀態變量轉換得到了四階非線性感應電機模型,通過反饋線性化推導出二階線性模型,同時實現了轉矩和磁鏈的解耦,故得到的線性模型是直觀、簡單的,大大簡化了控制器設計。DTC控制器的設計還使用了SMC環節,以提高系統的魯棒性,同時和傳統DTC控制相比,保留了傳統DTC控制的快速響應特性,同時還消除了傳統DTC控制帶來的轉矩和磁鏈脈動。最后通過感應電機驅動試驗平臺開展了對比試驗,驗證了新型控制方法的有效性。
1 感應電機模型的反饋線性化
經典的非線性系統的線性化方法是基于系統工作點進行一階近似,并忽略其高階動態。這在感應電機處于恒轉速時是適用的,但在感應電機的一些暫態中應用時將降低控制性能[7]。因此考慮反饋線性化方法,其不同于傳統的線性化,其效果是全局性的,而不僅僅局限于工作點附近[23]。通常反饋線性化較難實現,但通過對感應電機模型狀態變量的轉換,以及輸入的重新定義可以實現。
感應電機定子參考系下的狀態空間模型[12]:
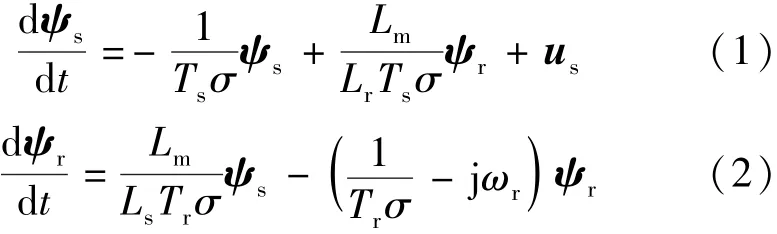
式中:ψs和ψr分別是定子磁鏈矢量和轉子磁鏈矢量;Rs和Rr分別為定子和轉子電阻;Ls,Lr和Lm分別為定子,轉子和激磁電感;Ts=Ls/Rs,Tr=Lr/Rr,σ=為轉子速度;us為定子電壓矢量,同時也是輸入變量。
為了實現反饋線性化,重新選擇狀態變量如下:
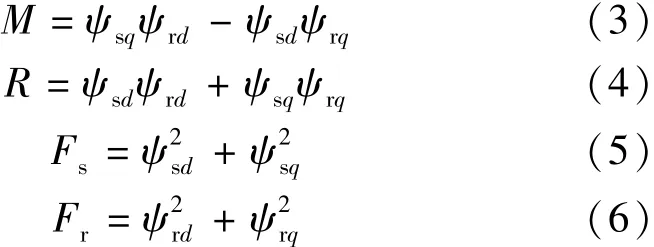
式中:ψsd和 ψsq分別是定子 d軸和 q軸磁鏈;ψrd和ψrq分別是轉子d軸和q軸磁鏈;M和轉矩相關,Fs和Fr分別是定子和轉子d,q軸磁鏈的平方和,而R取決于轉子和定子磁鏈。為了簡單起見,將M作為轉矩,而Fs作為定子磁鏈幅值,因此控制器設計為控制轉矩M和定子磁鏈幅值Fs,但也要保持狀態變量在Fr和R在邊界內。將狀態變量轉換后可以得到如下狀態方程:
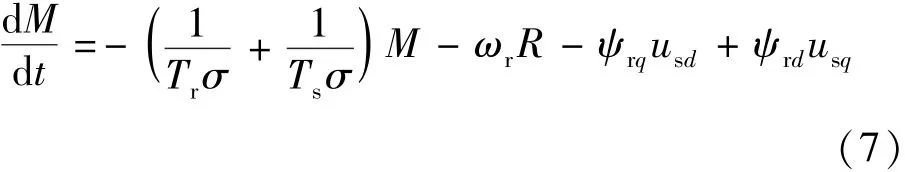
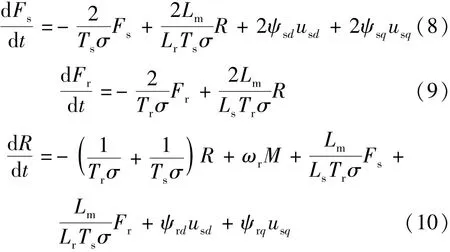
進一步將輸入變量重新定義為wd和wq:
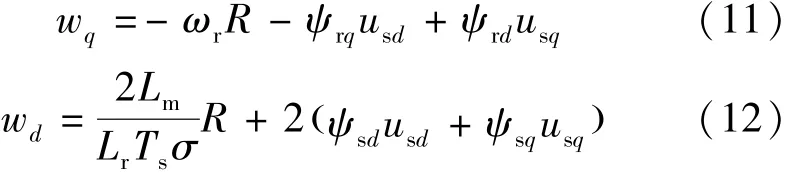
從而得到線性化的系統:
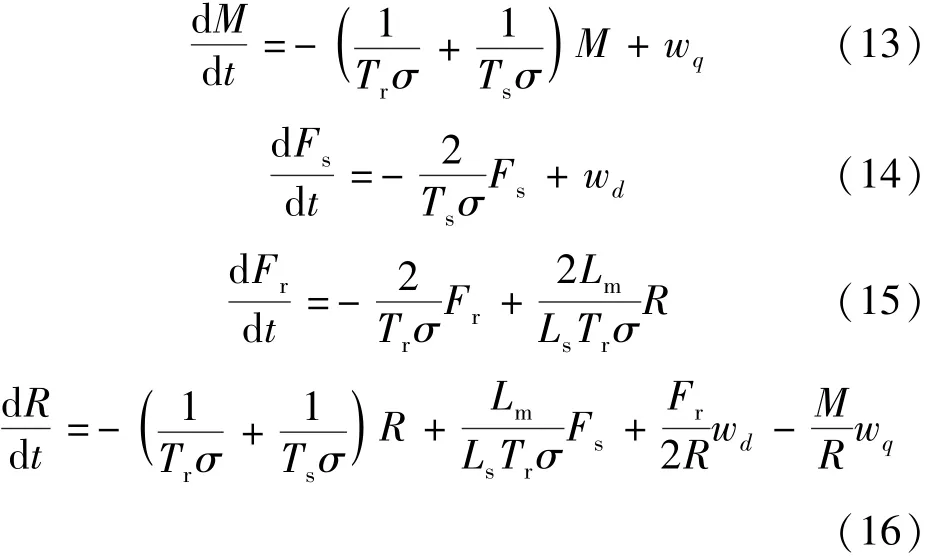
在重新定義輸入變量的式(11)和式(12)中,求解usd和usq可得:
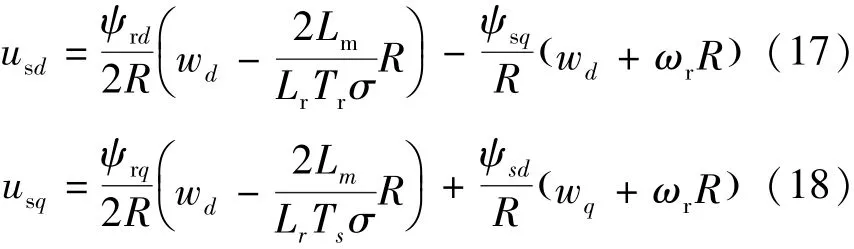
反饋線性化處理后,狀態變量Fs和M得到了解耦,進而簡化了感應電機驅動系統的控制器設計。同時考慮到對狀態變量Fs,Fr和M的方程求解得到的極點在左半平面,從而剩下的狀態變量R只要保證有界就可以實現輸入輸出的穩定性。而分析式(16)可以發現,只有當R為零的時候是無界的,這僅僅存在于定子或轉子磁鏈為零時,這在電機運行時不可能的,而在電機起動過程中只要保證控制器先進行磁鏈控制再進行轉矩控制即可。綜上,可以假設狀態變量R存在一個上邊界Rl,這在物理解釋上也是符合,即磁鏈存在飽和點,因而是有上邊界的。
2 結合反饋線性化和SMC的DTC方案
圖1為結合SMC和反饋線性化的DTC控制器框圖。從圖1中可以看出,控制器使用了簡單的轉速、轉矩和磁鏈觀測器,轉速閉環采用了PI調節器。
控制器的控制目標是實現轉矩和定子磁鏈幅值的控制,即實現DTC控制。前述已經將系統進行線性化處理,從而可以在線性化的模型基礎上設計。從式(13)和式(14)可以看出,狀態變量M和Fs已經實現了解耦,故很容易設計控制器來獲得輸入wd和wq。然后就是基于式(17)和式(18)來得到實際的輸入usd和usq。但考慮到控制器計算誤差是難以避免的,因此必須考慮控制器的魯棒性。實際控制輸入誤差可表示為線性狀態方程的等效誤差,根據式(13)可得到:

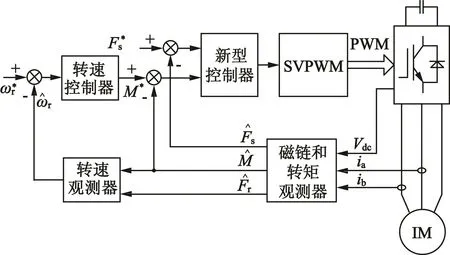
圖1 新型DTC控制器框圖
式中:gM代表了反饋線性化轉矩方程的不確定動態。式(13)中估計到的動態:
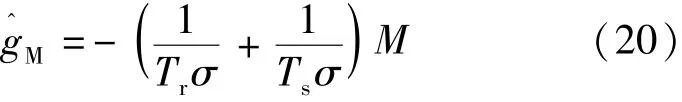
假設動態估計的誤差是有界的:
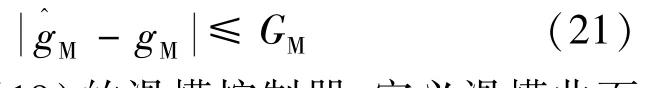
為了設計式(19)的滑模控制器,定義滑模曲面SM為轉矩誤差:

根據選擇的滑模曲面,控制率設計:
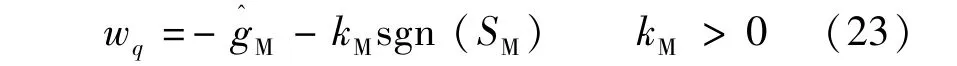
式(23)右邊第二項-kMsgn(SM)為校正控制。構造系統的Lyapunov函數為V=S2M/2。如果 Lyapunov函數的可微,且導數為負定,那么系統將收斂到滑模曲面。計算V的導數:
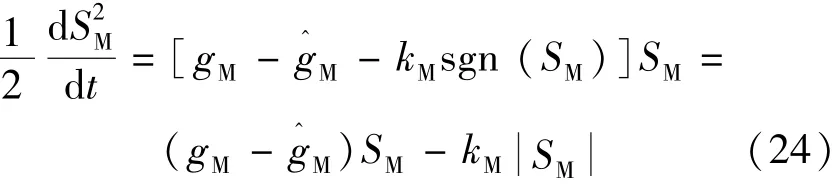
為了保證收斂的魯棒性,V的導數必須在一些不確定的條件下保證為負定。選擇校正控制增益kM如下:

這給出了滑動條件:

式中:ηM是一個正常數。式(25)中增益kM包括了GM以保證魯棒穩定性,增益kM還包括了ηM來控制收斂到滑模曲面的速度。較大的ηM將使得系統軌跡在一個更短的時間收斂,但是可能造成顫振。使用如下的積分滑模曲面可以得到相同的結果。
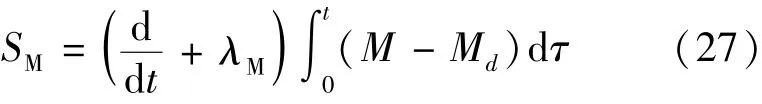
式中:λM是一個正常數,其決定當系統狀態點位于滑模曲面時,誤差收斂到零的速度。進而控制輸入wq可選擇:
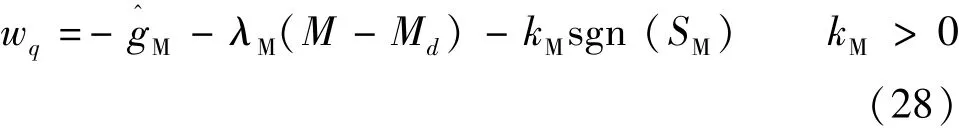
同時滑動條件為kM=GM+ηM。為了避免顫振,圍繞滑模曲面定義一個邊界BM(t)={x,|SM(x)|≤hM},其中hM>0決定了邊界與滑模曲面之間的厚度。在邊界內,將一個比例控制項增加到式(23)中,而在邊界外(|SM(x)|>hM),校正控制將使得系統趨于滑模曲面。
考慮到式(14)所描述的定子磁鏈動態和式(13)一樣,因此分析過程相同,不再累述,列出滑模曲面:

控制輸入wd設計:
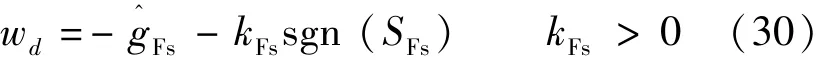
同樣使用一個狹窄的邊界圍繞滑模曲面,同時也加入比例控制,避免顫振。圖2為基于SMC和反饋線性化的轉矩和磁鏈控制器的框圖。從圖2中可以看出,控制律為式(23)和式(30),而參考電壓由式(17)和式(18)計算而來,最后的控制脈沖由空間矢量脈寬調制SVPWM實現。

圖2 基于SMC和反饋線性化的控制器框圖
3 控制器魯棒性分析和參數設計
下面將對控制器的魯棒性進行分析,包括對電機參數偏移和轉速測量誤差的魯棒性分析,因為這兩種擾動是對電機模型有影響的。首先假設這些不確定性都存在邊界,如式(21)所示,然后分析這些不確定性對校正增益選取的影響。
由不確定性導致的控制信號誤差設為Δusd和Δusq。為了分析不確定性對SMC設計的影響,先將式(17)和式(18)合并寫成矢量形式如下:雖然SMC控制器生成wd和wq時是沒有誤差的,但可以用等效誤差的方法替代us的誤差,即Δw=Δwd+jΔwq,從而式(31)可寫:
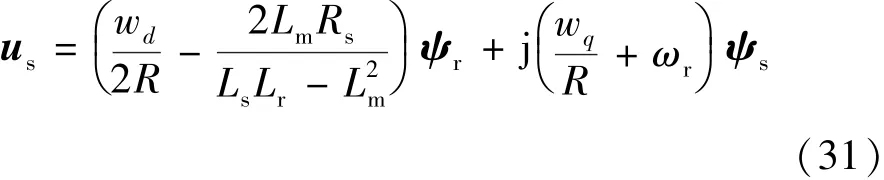
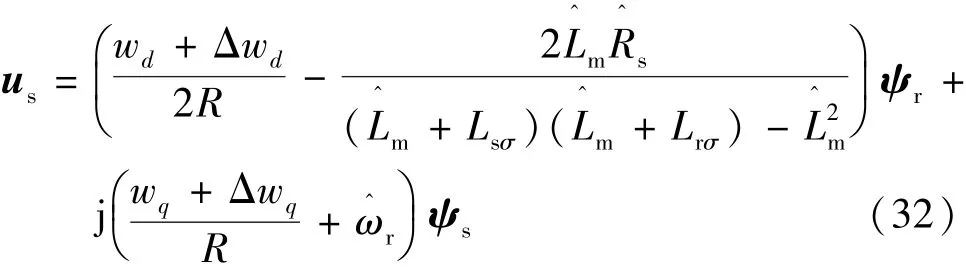
式中為測量的激磁電感;為測量的定子電阻;為測量的轉子轉速。聯立式(31)和式(32)可得:
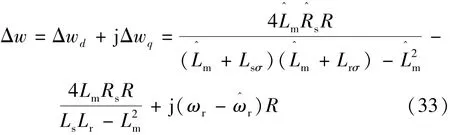
考慮wd和wq誤差后的M和Fs動態方程:
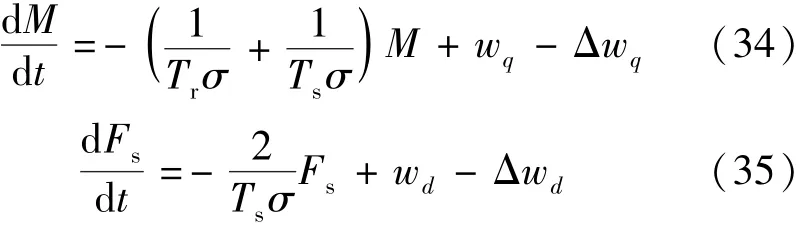
可以假定每個不確定參數的最大偏差和轉子速度的最大測量誤差是已知的。然后后續分析中設置ηM=10,ηFs=10,即設置一個固定動態響應速度后進行魯棒性分析。
3.1 轉速誤差魯棒性分析
轉速誤差將導致模型攝動,進而影響系統響應。轉速誤差對定子磁鏈沒有影響,但能改變轉矩,具體如下:
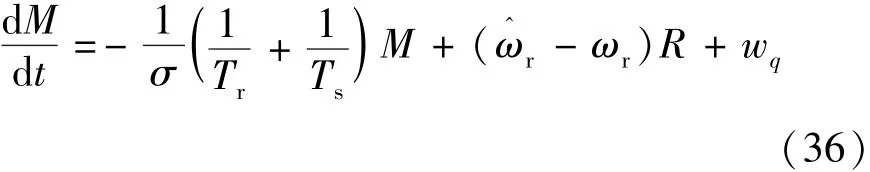
在已知最大轉速誤差后,可以設計合適的校正控制增益以保證魯棒性。基于后述表1的參數和標定測量,試驗用感應電機的R額定值為0.25 Ω,設轉速測量最大誤差為±10 rad/s,則相應GM=2.5,而kM=GM+ηM=12.5。在試驗中取kM=20,這樣誤差范圍有進一步的裕量。考慮到轉速誤差對磁鏈動態沒有影響,故設置kFs=ηFs+0=10。圖3為±10 rad/s轉速誤差時,在電機起動時的轉矩和磁鏈動態響應。從圖3中可以看出,轉矩控制受到轉速誤差的影響很小,保持了穩定,同時消除了轉矩脈動,這驗證了控制器對轉速誤差的魯棒性。
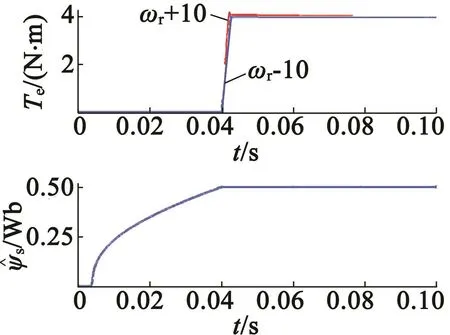
圖3 ±10 rad/s轉速誤差時的起動仿真波形
3.2 定子電阻誤差魯棒性分析
考慮到定子電阻隨溫度會產生變化,而定子電阻的變化將影響到定子磁鏈動態。引入定子電阻誤差后的定子磁鏈動態方程:
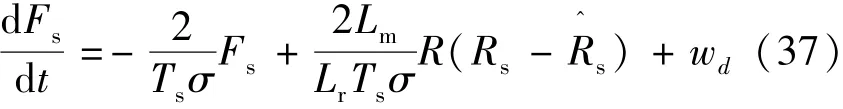
式中:是標稱定子電阻值;Rs為實際定子電阻值。設定子電阻最大誤差為±50%,將試驗用感應電機的相關參數代入進行計算(參數具體見表1),即對應模型攝動0.69=28.16。故選擇校正控制增益kFs=ηFs+GFs=40>38.16。考慮到定子電阻誤差對轉速動態沒有影響,因此保持之前的kM=20。圖4為±50%定子電阻誤差時,電機起動時的轉矩和磁鏈動態響應。從圖4中可以看出,定子電阻誤差對磁鏈響應時間稍有影響,但是穩定性和魯棒性依然較好。
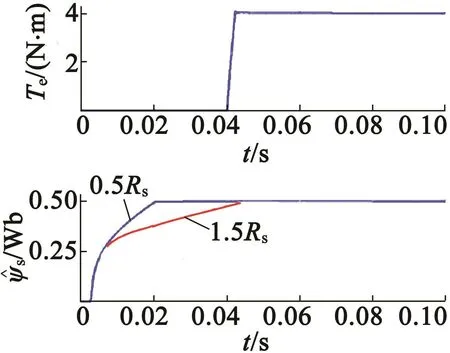
圖4 ±50%定子電阻誤差時的起動仿真波形
3.3 激磁電感誤差魯棒性分析
激磁電感可能由于磁飽和偏離其測量值,激磁電感的變化將影響到定子和轉子電感。但是對轉矩動態無影響,引入激磁電感誤差后的磁鏈動態方程如下:
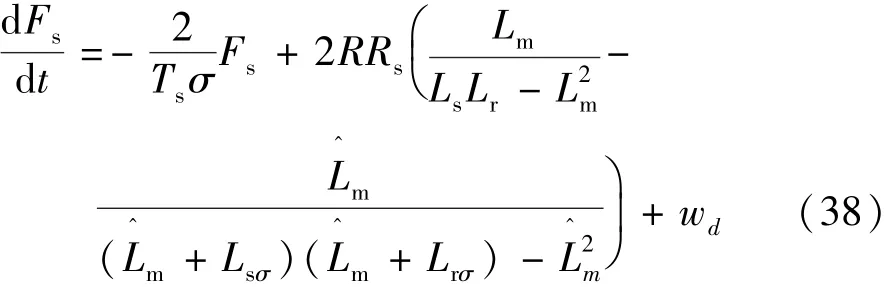
考慮最大的激磁電感誤差為±30%,設為標稱激磁電感,則有0.7在式(38)中等號右邊括號中的項設為ΔL,其值取決于Lm,當Lm取下限值時,ΔL=-0.424 67,當Lm取上限值時,ΔL=-0.237 16。為了保證最大的魯棒穩定性,使用|ΔL|的最大值進行參數設計。|ΔL|最大時對應擾動為GFs=2RRs×0.424 67=0.49,所以取 kFs=12>10.49。考慮到激磁電感對轉矩動態無影響,因此保持之前的kM=20。圖5為±30%激磁電感誤差時,電機起動時的轉矩和磁鏈動態響應。從圖5中可以看出,激磁磁鏈誤差對磁鏈響應時間稍有影響,但是穩定性和魯棒性依然較好。
綜上所述,南通范氏家族的家風在宏觀方面體現出“萬家憂樂盡關心”的民胞物與之情,在微觀方面的表現也涵蓋了溫、良、恭、儉、讓、孝、悌、忠、信等各個方面。這些南通范氏家族世代傳承的美好品德,也是維護范氏家族聲譽不墜的行為準則,更是范氏家族延續四百五十年之久的傳家之寶。南通范氏并非簪纓望族,但由于對文正家風的恪守,對詩禮書香傳家的踐行,使范氏家族成為南通乃至江蘇的文化世家,其魯殿靈光的“家風”與“家學”對今天的教育體制具有諸多啟示意義,對南通范氏“家風”的梳理與解讀也有助于弘揚中華民族的傳統家庭美德,為樹立優良家風、構建和諧社會提供可資借鑒的模板。
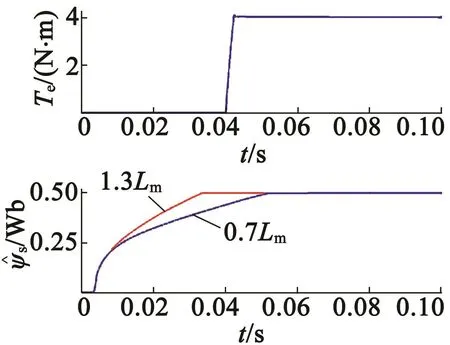
圖5 ±30%激磁電感誤差時的起動仿真波形
綜上分析,新型控制算法中的參數設計遵循以下原理,首先根據需要系統需要的動態選擇ηM和ηFs,然后根據參數不確定性的范圍選擇GM和GFs。在確定ηM,ηFs,GM和GFs后,選擇一個滑模轉矩控制器增益大于ηM+GM,滑模磁鏈控制器增益大于ηFs+GFs,這將使得系統具有較強的魯棒性。
4 試驗驗證
為了驗證新型控制策略的有效性,基于感應電機驅動試驗平臺進行了對比試驗驗證。試驗驗證的思路:首先對比傳統線性化DTC[7]和反饋線性化DTC控制方案[11]的試驗結果,然后再對比反饋線性化的DTC和結合滑模控制和反饋線性化的DTC控制方案的試驗結果,其中經典反饋線性化的DTC控制方案的控制器框圖如圖6所示。
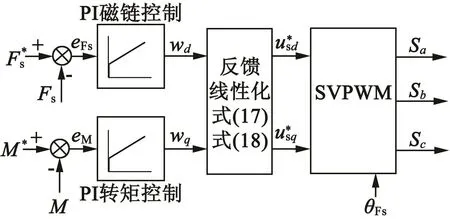
圖6 傳統反饋線性化的控制器框圖
具體的試驗用感應電機額定功率為1.6 kW,具體電機參數如表1所示。試驗平臺結構如圖7所示。其中變頻器采用丹佛斯商用變頻器,額定功率3.2 kVA,控制器核心硬件為德州儀器公司的TMS320F28335芯片,采樣頻率和開關頻率設置為10 kHz,具體的控制器參數如表2所示。
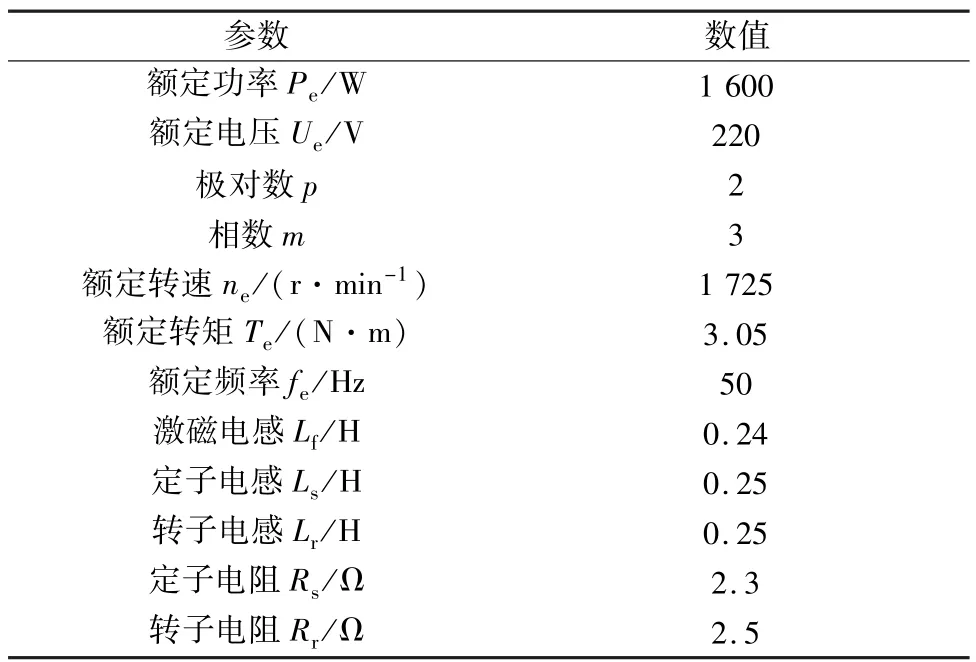
表1 感應電機主要參數
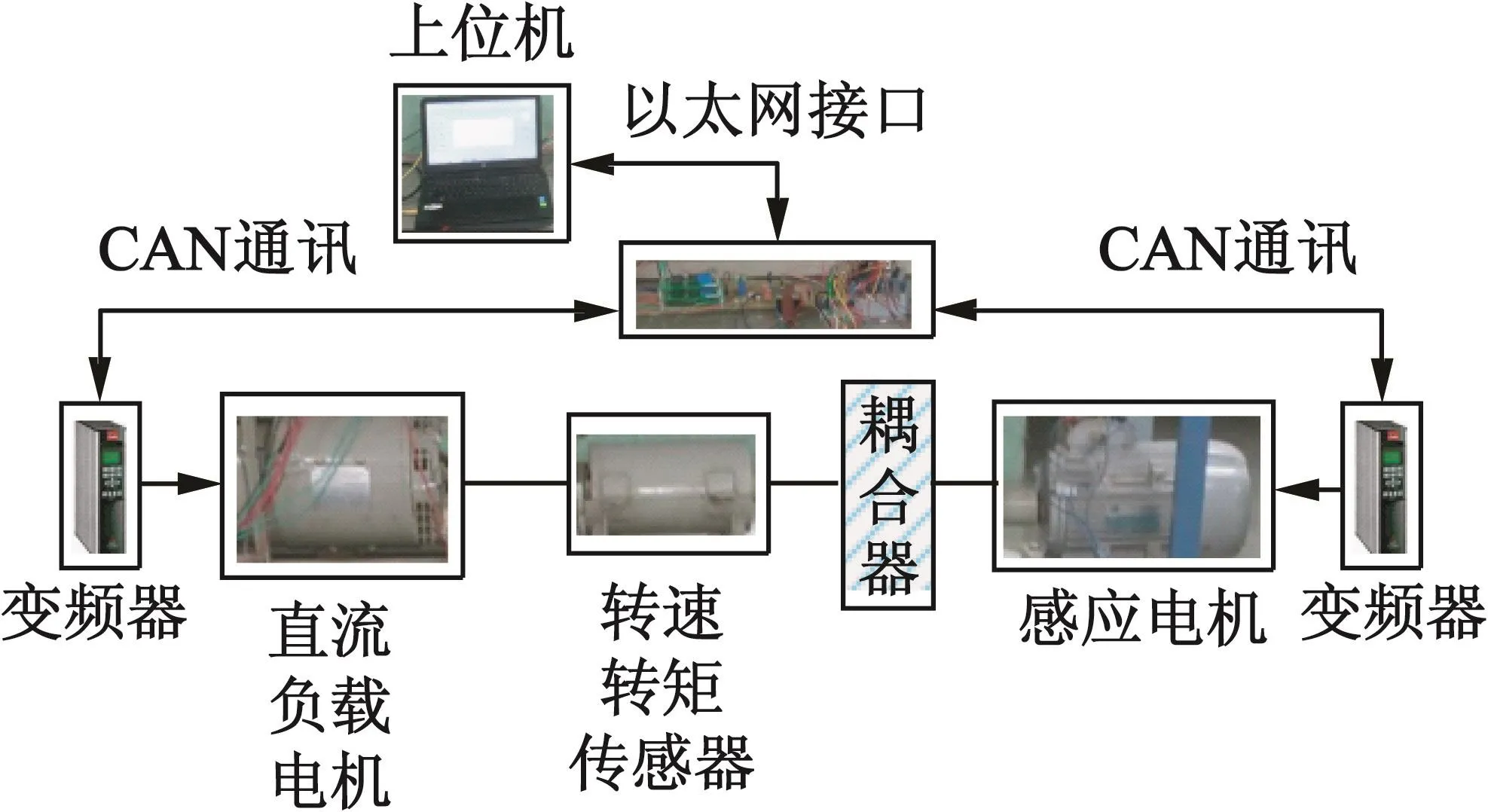
圖7 感應電機驅動試驗平臺結構
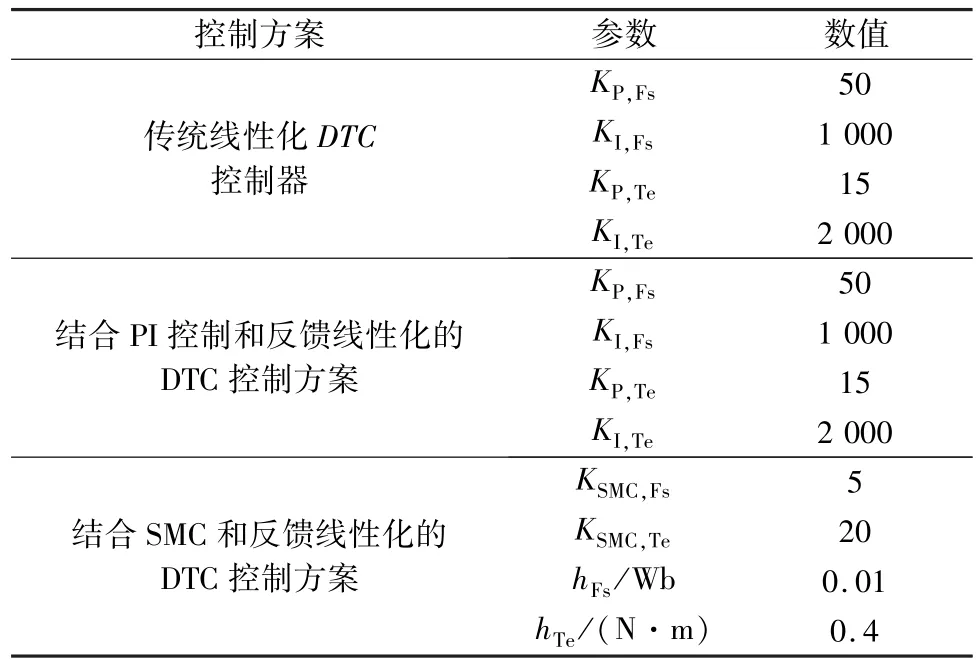
表2 控制器主要參數
(1)傳統線性化和反饋線性化DTC對比試驗結果
為了保證對比的客觀性,傳統線性化DTC方案的PI參數和反饋線性化DTC方案的PI參數是一致的,如表2所示。圖8和圖9分別是兩種控制方案下轉矩和磁鏈階躍響應對比。從對比試驗結果可以看出,經典的反饋線性化DTC方案的轉矩和磁鏈響應要比傳統線性化DTC方案快,磁鏈波形的顫振更小。
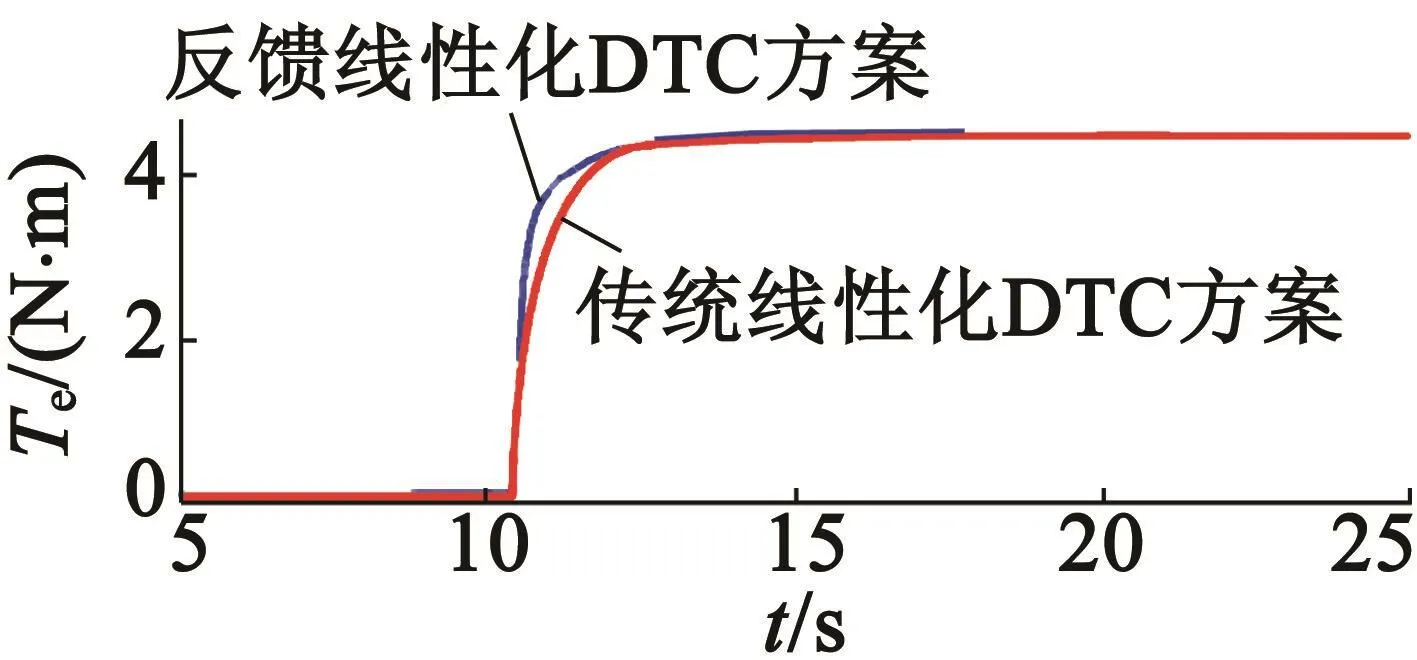
圖8 傳統線性化和反饋線性化DTC的轉矩響應對比
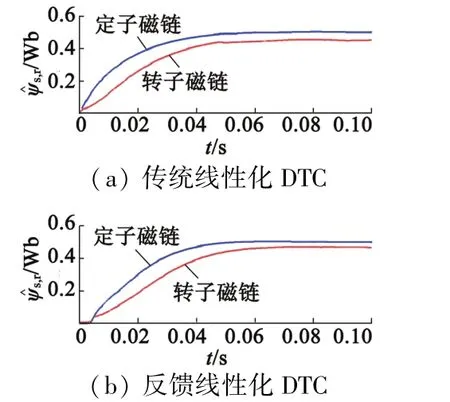
圖9 傳統線性化和反饋線性化DTC的磁鏈響應對比
(2)傳統反饋線性化和結合SMC的反饋線性化DTC對比試驗結果
在試驗中,配合使用的磁鏈和轉矩觀測器都是較為簡單的(反電動勢低通濾波),且兩種方案是一致的。圖10為采用結合SMC和反饋線性化的DTC方案時,0至1.5倍額定轉矩的階躍響應。從圖10中可以看出,轉矩變化時,磁鏈沒有改變,說明這是一種解耦的控制方法,同時轉矩在小于2 ms的時間內即達到指定值,動態響應很快,從放大拐點圖中可以明顯地看出,因為控制器計算收斂很快。與此同時,轉矩脈動還很小。圖11為定子和轉子磁鏈從0階躍至0.5 Wb的波形,響應速度快且無顫振。
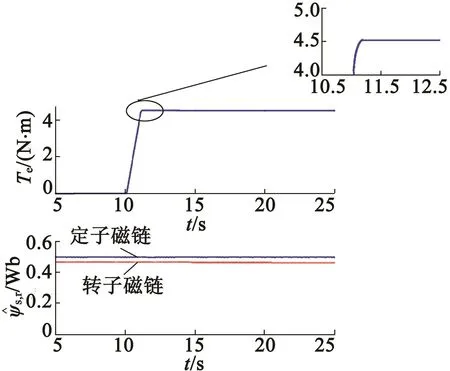
圖10 結合SMC和反饋線性化DTC的轉矩響應
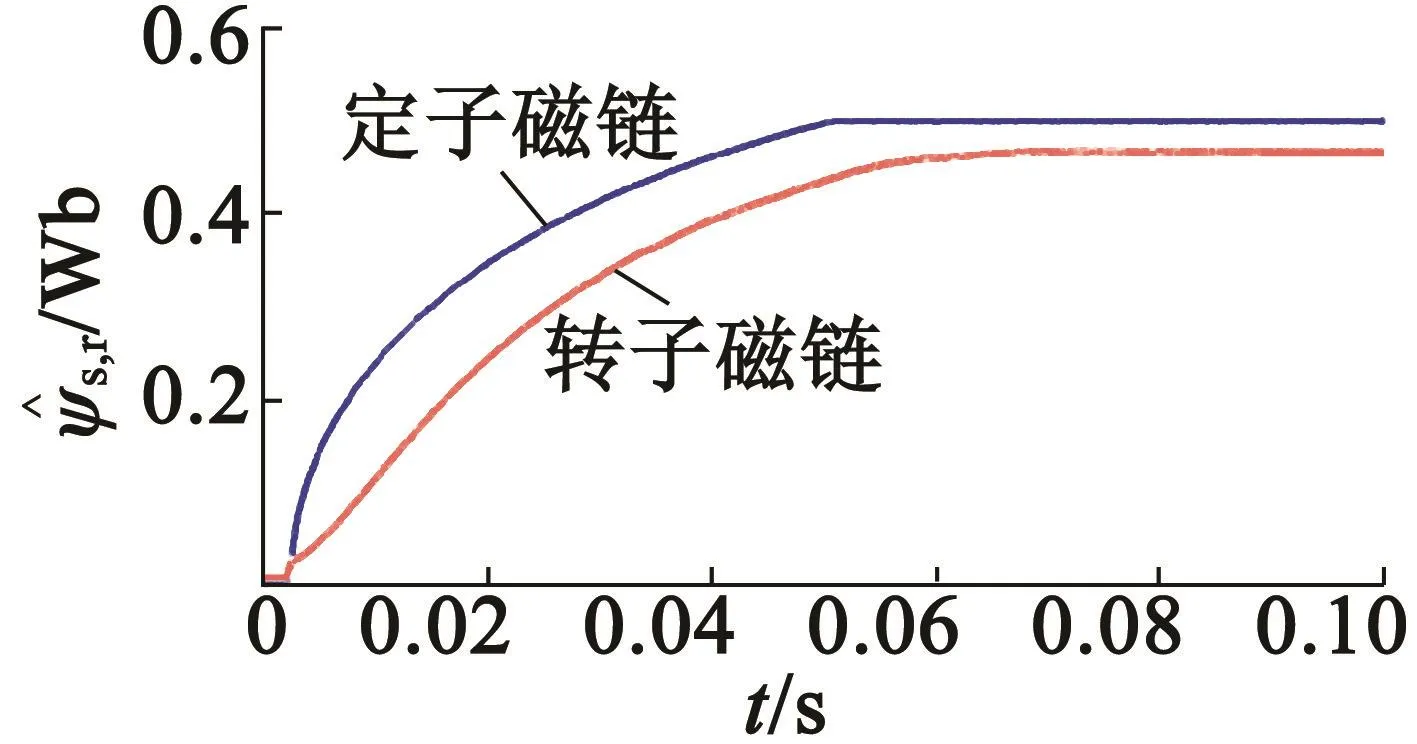
圖11 結合SMC和反饋線性化DTC的磁鏈響應
圖12 和圖13分別為傳統反饋線性化和結合SMC的反饋線性化DTC對比試驗波形,包括了估計轉速、實測轉速、轉矩和定轉子磁鏈波形。從圖中可以看出,轉速響應動態是相似的,但是對比圖10和圖11中的轉矩和磁鏈響應曲線,可以看出結合SMC和反饋線性化的DTC方案魯棒性較強,在轉速動態時轉矩脈動和磁鏈波動較小,具體傳統反饋線性化方案時的轉矩脈動大于0.3 N·m,磁鏈波動大于0.04 Wb,而新型方案的轉矩脈動小于0.2 N·m,磁鏈波動小于0.02 Wb。兩種方案下都進行了電機正向運行與反向運行的試驗,正向運行時轉矩達到了4.4 N·m,反向運行時轉矩為-4.4 N·m。從轉矩曲線可以看出,轉矩脈動集中在勻速段,而加速段沒有,這是因為加速過程中PI控制器和滑模磁鏈控制器接近飽和輸出最大值,而在勻速中進行了調節,進而出現了轉矩脈動。
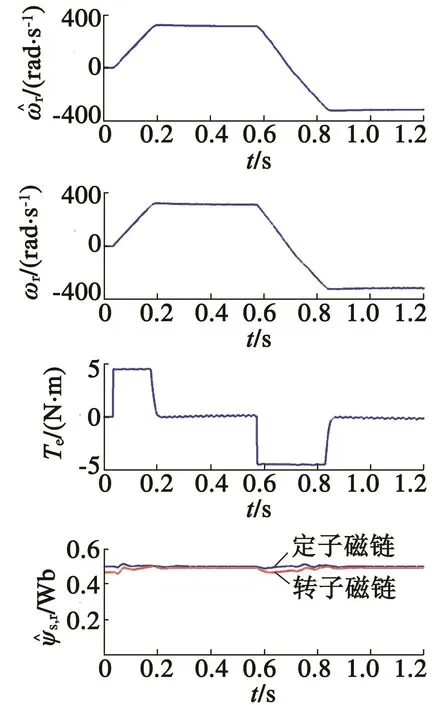
圖12 傳統反饋線性化DTC的試驗波形
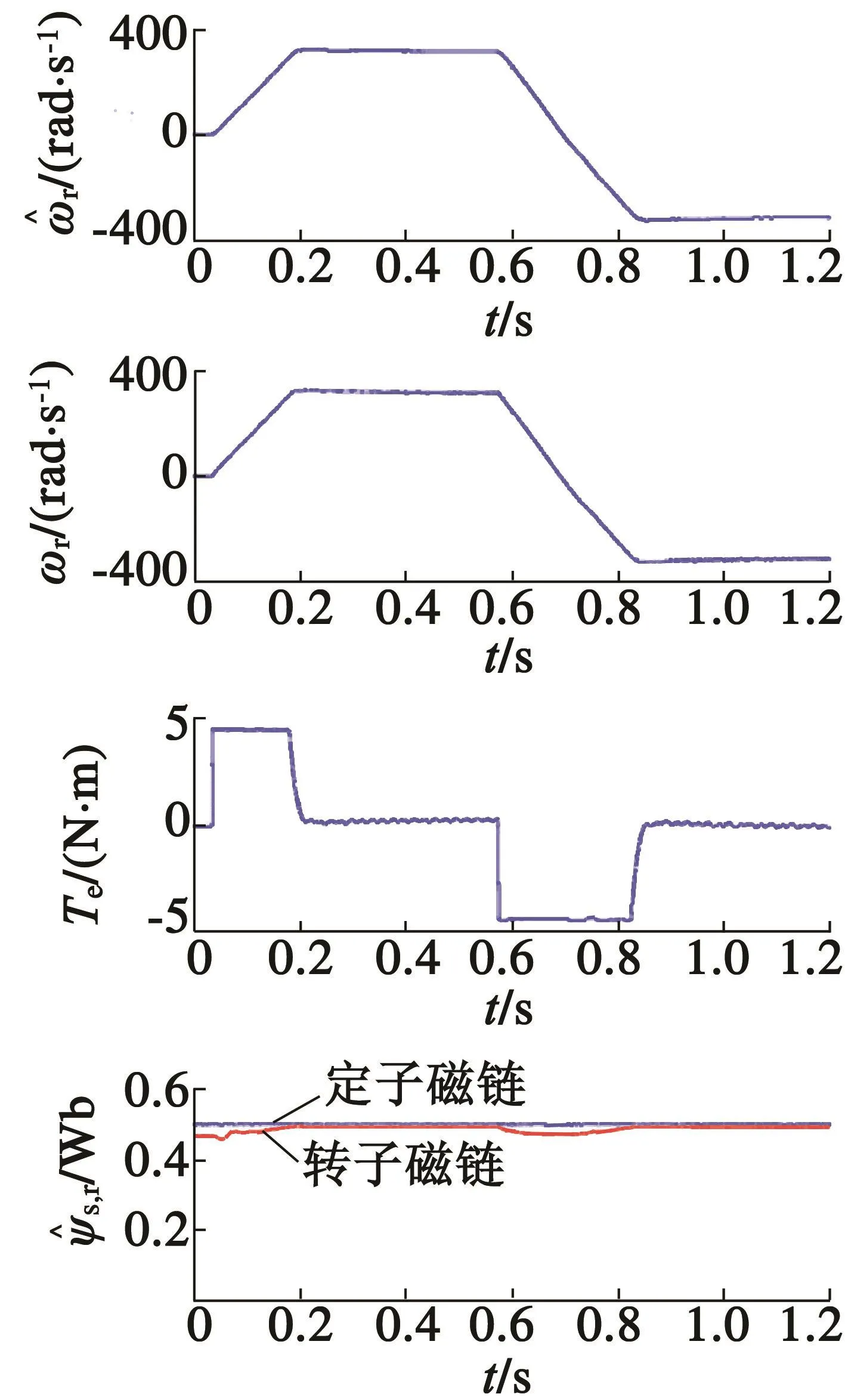
圖13 結合SMC和反饋線性化DTC的試驗波形
5 結 語
本文提出了一種新型的結合滑模控制和反饋線性化的直接轉矩控制方案。首先基于反饋線性化得到了一個解耦的感應電機線性模型;然后結合滑模控制設計了控制器;最后進行了對比試驗。現總結主要結論如下:
1)新型控制策略針對不確定性可以調整自身控制參數,進而實現較強的魯棒性。同時設計滑模曲面的邊界包圍實現了響應速度的調節。
2)對比試驗結果表明,和傳統DTC控制相比,新型控制策略保留了直接轉矩控制的優點,并顯著降低了轉速動態時的磁鏈波動,是一種效果更優的控制策略。

