(2+1)維非線性分?jǐn)?shù)階Zoomeron方程的新精確解

黃 春, 孫峪懷, 李 釗, 張 健

(1. 四川師范大學(xué) 數(shù)學(xué)與軟件科學(xué)學(xué)院, 四川 成都 610066; 2. 四川職業(yè)技術(shù)學(xué)院 應(yīng)用數(shù)學(xué)與經(jīng)濟(jì)系, 四川 遂寧 629000)

(2+1)維非線性分?jǐn)?shù)階Zoomeron方程的新精確解

黃 春1,2, 孫峪懷1*, 李 釗1, 張 健1

(1. 四川師范大學(xué) 數(shù)學(xué)與軟件科學(xué)學(xué)院, 四川 成都 610066; 2. 四川職業(yè)技術(shù)學(xué)院 應(yīng)用數(shù)學(xué)與經(jīng)濟(jì)系, 四川 遂寧 629000)

通過復(fù)變換將高維非線性分?jǐn)?shù)階偏微分方程轉(zhuǎn)化為整數(shù)階常微分方程,然后利用擴(kuò)展的(G′/G)-展開法,構(gòu)建(2+1)維非線性分?jǐn)?shù)階Zoomeron方程的新精確解,其中包括含參數(shù)的雙曲函數(shù)解、三角函數(shù)解和有理數(shù)解.

(2+1)維非線性分?jǐn)?shù)階Zoomeron方程; 擴(kuò)展的(G′/G)-展開法; 精確解

1 預(yù)備知識

非線性分?jǐn)?shù)階偏微分方程是整數(shù)階偏微分方程的推廣,它比整數(shù)階偏微分方程更全面地解釋實際現(xiàn)象,并且能夠深刻描述與反映物體內(nèi)在的性質(zhì).非線性分?jǐn)?shù)階偏微分方程在流體力學(xué)、材料力學(xué)、生物學(xué)、等離子體物理學(xué)、金融學(xué)、化學(xué)等許多領(lǐng)域有著廣泛的應(yīng)用,因此研究非線性分?jǐn)?shù)階偏微分方程的性質(zhì)以及解的情況具有重要的意義.

(2+1)維非線性分?jǐn)?shù)階Zoomeron方程[1-5]

(1)

修正的Riemann-Liouville分?jǐn)?shù)階導(dǎo)數(shù)

(2)

修正的Riemann-Liouville分?jǐn)?shù)階導(dǎo)數(shù)的性質(zhì):

(3)

(4)

(5)

(2+1)維非線性分?jǐn)?shù)階Zoomeron方程,最早由F.Calogero等[1]提出:當(dāng)α=1,方程(1)是一個隱式非線性演化方程;文獻(xiàn)[2]通過分?jǐn)?shù)首次積分法獲得分?jǐn)?shù)階Zoomeron方程的一些精確解;文獻(xiàn)[3-5]分別用指數(shù)函數(shù)展開法、(G′/G)-展開法、首次積分法獲得該方程在整數(shù)階情形下的精確解.

最近,LiZ.B.等[7]提出如(7)式所表達(dá)的復(fù)變換將分?jǐn)?shù)階偏微分方程轉(zhuǎn)化為整數(shù)階常微分方程,該變換被廣泛運用在非線性分?jǐn)?shù)階偏微分方程的求解中.構(gòu)建非線性分?jǐn)?shù)階偏微分方程精確解的方法主要包括:分?jǐn)?shù)指數(shù)函數(shù)展開法[8-10]、分?jǐn)?shù)首次積分法[11-13]、分?jǐn)?shù)Riccati映射法[14-15]、分?jǐn)?shù)(G′/G)-展開法[16-18]等.本文通過作復(fù)變換將高維非線性分?jǐn)?shù)階偏微分方程轉(zhuǎn)化為整數(shù)階常微分方程,然后運用擴(kuò)展的(G′/G)-展開法構(gòu)建(2+1)維非線性分?jǐn)?shù)階Zoomeron方程的新精確解.

2 方法描述

考慮下面的非線性分?jǐn)?shù)階偏微分方程

(6)

其中,u=u(x,y,t)是未知函數(shù),P是u及u的關(guān)于x、y、t各階偏導(dǎo)數(shù)的多項式.

步驟 1 通過作復(fù)變換

(7)

其中,l和c為任意常數(shù),且ω≠0.

將方程(6)轉(zhuǎn)化為只含變量ξ的整數(shù)階常微分方程

(8)

步驟 2 設(shè)方程(8)的解為(G′/G)多項式形式

(9)

其中,G=G(ξ)滿足輔助方程

(10)

λ和μ為常數(shù).正整數(shù)N可以通過平衡(8)式中最高階導(dǎo)數(shù)項和非線性項確定.

步驟 3 將方程(9)代入(8)式,并利用方程(10)合并(G′/G)的相同冪次項,然后令(G′/G)的各次冪系數(shù)為零.

步驟 4 求解上述以ai(i=-N,…,0,…,N)為未知量的代數(shù)方程組,借助于Maple軟件,從而獲得方程(6)的精確解.

下面將運用此方法來構(gòu)建(2+1)維非線性分?jǐn)?shù)階Zoomeron方程的新精確解.

3 運用與結(jié)果

首先對方程(1)作變換

得

(11)

將方程(11)左右兩邊同時積分2次,取第二次積分常數(shù)為零,可得

(12)

其中r為非零積分常數(shù).設(shè)方程(12)有如下形式的解

(13)

通過平衡方程(12)中的u3和u″,則有3N=N+2,有N=1,方程(13)化為

(14)

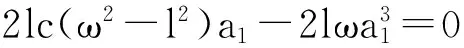
(15)

求解這個方程組可得:

(16)

(17)

情形 1 當(dāng)λ2-4μ>0時,方程(1)有如下形式的雙曲函數(shù)解:

特別地,當(dāng)C1=0,C2≠0時有

(19)

當(dāng)C1≠0,C2=0時有

(20)

(21)

其中

C1和C2為任意常數(shù).

情形 2 當(dāng)λ2-4μ<0時,方程(1)有如下形式的三角函數(shù)解:

特別地,當(dāng)C1=0,C2≠0時有

(23)

當(dāng)C1≠0,C2=0時有

(24)

(25)

其中

C1和C2為任意常數(shù).

情形 3 當(dāng)λ2-4μ=0時,方程(1)有如下形式的有理函數(shù)解:

(26)

(27)

其中

C1和C2為任意常數(shù).

4 結(jié)果與討論

本文通過作(7)式所表達(dá)的復(fù)變換將高維非線性分?jǐn)?shù)階偏微分方程轉(zhuǎn)化為整數(shù)階常微分方程,然后利用擴(kuò)展的(G′/G)-展開法構(gòu)建(2+1)維非線性分?jǐn)?shù)階Zoomeron方程的新精確解,其中包括含參數(shù)的雙曲函數(shù)解、三角函數(shù)解和有理數(shù)解.文中所得結(jié)果u12(ξ)和u11(ξ)與文獻(xiàn)[2]中的u1(ξ)和u2(ξ)一致,u32(ξ)和u31(ξ)與文獻(xiàn)[2]中的u4(ξ)和u5(ξ)一致,u2、u4和u6是文獻(xiàn)中未曾出現(xiàn)的結(jié)果.本文構(gòu)建了分?jǐn)?shù)階Zoomeron方程的新精確解,同時也說明擴(kuò)展的(G′/G)-展開法是求解一類非線性分?jǐn)?shù)階偏微分方程行之有效的方法.

[1] CALOGERO F, DEGASPERIS A. Nonlinear evolution equations solvable by the inverse spectral transform[J]. Il Nuovo Cimento,1976,B2(32):201-242.

[2] ZAYE E M E, AMER Y A. The first integral method and its application for finding the exact solutions of nonlinear fractional partial differential equations in the mathematical physics[J]. Inter J Phys Sci,2014,8(9):174-183.

[3] KHAN K, AKBAR M A. Traveling wave solutions of the (2+1)-dimensional Zoomeron equation and the Burgers equations via the MSE method and the exp-function method[J]. Ain Shams Engineering J,2014,5(1):247-256.

[5] ABAZARI R. The solitary wave solutions of Zoomeron equation[J]. Appl Math Sci,2011,59(5):2943-2949.

[5] BEKIR A, TASCAN F, üNSAL ?. Exact solutions of the Zoomeron and Klein-Gordon-Zakharov equations[J]. J Association Arab Univ Basic Appl Sci,2015,17:1-5.

[6] JUMARIE G. Modified Riemann-Liouville derivative and fractional Taylor series of nondifferentiable functions further results[J]. Comput Math Appl,2006,51(9):1367-1376.

[7] LI Z B, HE J H. Fractional complex transform for fractional differential equations[J]. Appl Math Comput,2010,15(5):970-973.

[8] GüNER ?, BEKIR A, PANDIR Y. Solving nonlinear space-time fractional differential equations using the exp-function method[J]. AIP Conf Proc,2015,1648(1):1-5.

[9] YAN L M, XU F S. Generalized exp-function method for nonlinear space-time fractional differential equations[J]. Thermal Sci,2014,18(5):1573-1576.

[10] JIA S M, HU M S, CHEN Q L, et al. Exact solution of fractional Nizhnik-Novikov-Veselov equation[J]. Thermal Sci,2014,18(5):1716-1717.

[11] AMINIKHAH H, SHEIKHANI A R, REZAZADEH H. Exact solutions for the fractional differential equations by using the first integral method[J]. Nonlinear Engineering,2015,4(1):15-22.

[12] LU B. The first integral method for some time fractional differential equations[J]. J Math Anal Appl,2012,395(2):684-693.

[13] ESLAMI M, VAJARGAH F B, MIRZAZADEH M, et al. Application of first integral method to fractional partial differential equations[J]. Indian J Phys,2014,88(2):177-184.

[14] FENG Q H. A new fractional projective riccati equation method for solving fractional partial differential equations[J]. Commun Theory Phys,2014,62(2):167-172.

[15] ZHANG Y F, FENG Q H. Fractional riccati equation rational expansion method for fractional differential equations[J]. Appl Math Inform Sci,2013,7(4):1575-1584.

[16] ZHANG Y W. Solving STO and KD equations with modified Riemann-Liouville derivative using improved (G′/G)-expansion function method[J]. IAENG Inter J Appl Math,2015,45(1):16-22.

[17] ZHENG B. (G′/G)-expansion method for solving fractional partial differential equations in the theory of mathematical physics[J]. Commun Theory Phys,2012,58(5):623-630.

[18] YOUNIS M, ZAFAR A. Exact solution to nonlinear differential equations of fractional order via (G′/G)-expansion method[J]. Appl Math,2013,5(1):1-6.

2010 MSC：35K05

(編輯 李德華)

Received date:2015-02-03

Foundation Items:This work is supported by National Natural Science Foundation of China(No.11371267 and 11571245) and Basic Project of Sichuan Provincial Science and Technology Department(No.2016JY0204)

Construction of the New Exact Solutions for the (2+1) Dimensional Nonlinear Fractional Zoomeron Equation

HUANG Chun1,2, SUN Yuhuai1, LI Zhao1, ZHANG Jian1

( 1.CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan;2.DepartmentofAppliedMathematicsandEconomy,SichuanVocationalandTechnicalCollege,Suining629000,Sichuan)

(2+1) dimensional nonlinear fractional Zoomeron equation has been discussed. Firstly, the (2+1) dimensional nonlinear fractional Zoomeron equation has been converted to a nonlinear ordinary differential equation by using the fractional complex transformation. Then, the extended (G′/G)-expansion method is used to construct exact solutions. A series new explicit solutions are obtained, which include hyperbolic function solutions, trigonometric function solutions and rational solutions, more results than existing ones.

(2+1) dimensional nonlinear fractional Zoomeron equation; extended (G′/G)-expansion method; exact solutions

2015-07-08

國家自然科學(xué)基金(11371267)和四川省教育廳自然科學(xué)重點基金(2012ZA135)

O175.29

A

1001-8395(2017)01-0051-04

10.3969/j.issn.1001-8395.2017.01.008

*通信作者簡介：孫峪懷(1963—),男,教授,主要從事數(shù)學(xué)物理的研究,E-mail:sunyuhuai63@163.com