一道常見題型的拓展分析

揚州大學附中東部分校(211400) 朱云峰●

?

一道常見題型的拓展分析

揚州大學附中東部分校(211400)
朱云峰●

本文主要探討一道常見題型的深挖拓展，增加學生的拓展面，提高教學效率，更好地減輕學生的學習負擔.

機械能守恒;圓周運動;深化;挖掘

中學物理中圓周運動與機械能守恒經常是結合起來考查學生的.筆者對一道圓周運動與機械能守恒相結合的常見題型,深入探究,拓展分析,并與解答,談談我的看法,題目如下：

原題 用長為L的細繩系著一個質量為m的小球固定在O點,繃緊細繩,在水平位置靜止釋放小球,在O點正下方有根釘子O1,使得小球圍繞釘子O1做圓周運動,求小球做圓周運動的半徑,如圖1.

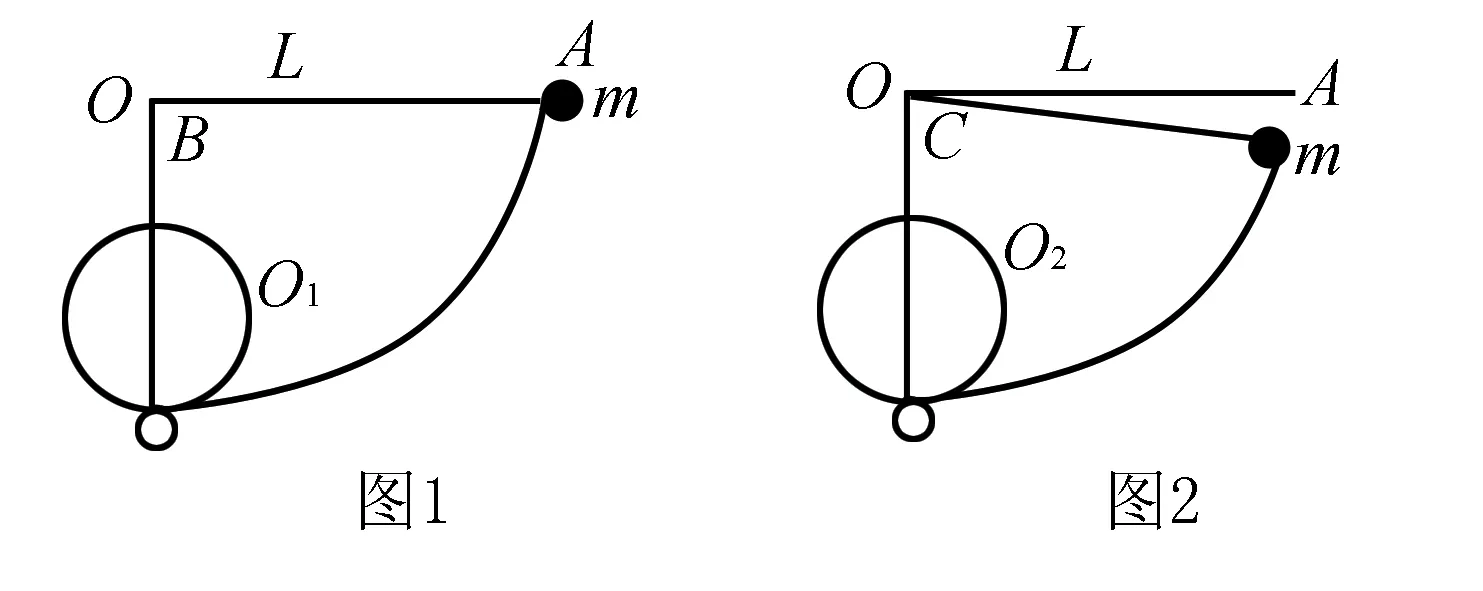
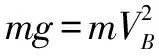
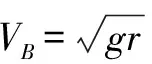
拓展一 : 如果小球低于水平位置,且與水平位置成θ角,繃緊細繩,靜止釋放,在O點正下方某處有一釘子O2, 使得小球圍繞釘子O2做圓周運動,求小球做圓周運動的半徑,如圖2.

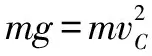
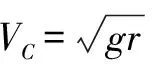
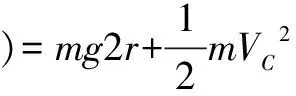
比較釋放前小球離零勢能面的高度h前和釋放后小球圍繞釘子O2做圓周運動到達C點時離零勢能面的高度h后

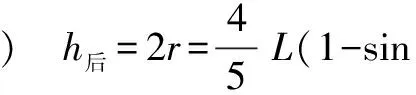
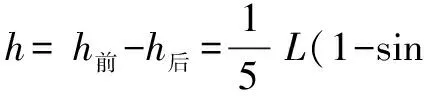
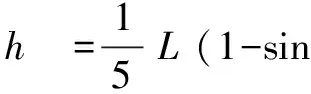
拓展分析二 如果小球高于水平位置,且與水平位置成θ角,繃緊細繩,靜止釋放,在O點正下方某處有一釘子O3使得小球圍繞釘子O3圓周運動,求小球做圓周運動的半徑,如圖3.

解 小球從A點到A1自由落體運動，由機械能守恒得：

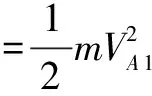
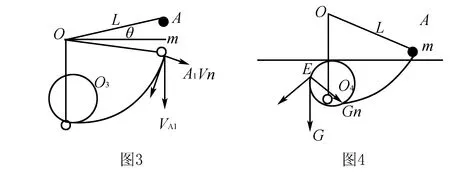
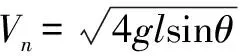
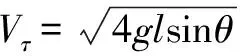
在A1處由于繩子繃緊過程中，拉力做功，小球在A1處的法向速度瞬間為零.

A1點到D點機械能守恒，以小球為研究對象得：

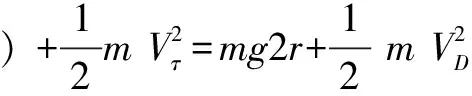
小球在D處恰好做圓周運動,在最高點B處,由重力提供向心力

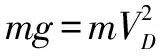
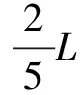
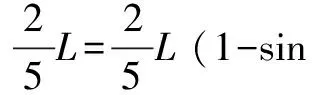
化簡：sinθ=2sinθcos2θ

錯解 點A、E在等高的水平線上，由于機械能守恒，小球能回到E點，且 VE=0

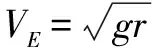
正確解法：(1)小球在A點的機械能：

EKA=mg2r

小球到達E點的最小機械能為：

EKA>EKE

∴小球不能到達點E

(2)假釋小球運動到點D離開圓形軌道，做斜拋運動，連接O4D，與豎直方向夾角為α，α確定，故D點位置確定.

如圖4，在D處小球由重力的一個分力Gn= Gcosθ= mgcosθ⑧提供向心力，即Gn= f向=mVD2/r ⑨

根據(A、D兩點)機械能守恒：

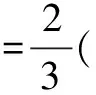
向上面這道普通題型的深化，挖掘，對學生思維的發展，知識的掌握和靈活運用，有重要的影響.在教學工作中，我們也要不斷的深化學習.

G

B

1008-0333(2017)10-0072-02