基于MATLAB GUI的高等數(shù)學(xué)計(jì)算機(jī)輔助教學(xué)演示系統(tǒng)的開發(fā)
劉兵


摘 要: 根據(jù)高等數(shù)學(xué)課程的教學(xué)現(xiàn)狀和高等數(shù)學(xué)課程中重要數(shù)學(xué)概念的幾何意義及其所蘊(yùn)含的數(shù)學(xué)思想,利用MATLAB語言進(jìn)行GUI編程,開發(fā)出了針對(duì)于高等數(shù)學(xué)各個(gè)教學(xué)模塊的輔助教學(xué)演示系統(tǒng)。該系統(tǒng)演示內(nèi)容全面、交互性好、操作簡(jiǎn)單、演示直觀性強(qiáng)利于對(duì)概念的理解。應(yīng)用該系統(tǒng),可激發(fā)學(xué)生的學(xué)習(xí)興趣,改善教學(xué)效果,提高教學(xué)質(zhì)量。
關(guān)鍵詞: 高等數(shù)學(xué); MATLAB; GUI編程; 教學(xué)輔助系統(tǒng); 演示模塊
中圖分類號(hào):G642 文獻(xiàn)標(biāo)志碼:A 文章編號(hào):1006-8228(2017)05-64-04
Design and implementation of higher mathematics computer aided teaching
demonstration system based on MATLAB GUI
Liu Bing1,2
(1. Chengde Petroleum College, Chengde, Hebei 067000, China; 2. Hebei Instruments and Meters Engineering Technology Research Center)
Abstract: According to the teaching status of higher mathematics course and the geometric meaning of important mathematical concepts and the mathematical thought that it contains, in the higher mathematics course, using MATLAB language for GUI programming, a higher mathematics computer aided teaching demonstration system for each teaching module is developed. The system is comprehensive in content, interactive, simple operation and intuitive demonstration, which is beneficial to the understanding of the concepts. The application of this system can stimulate students' interest in learning, and improve the teaching effect and teaching quality.
Key words: higher mathematics; MATLAB; GUI programming; computer aided teaching system; demonstration module
0 引言
高等數(shù)學(xué)[1]課程一直是高等院校絕大多數(shù)專業(yè)的必修基礎(chǔ)性課程。在傳統(tǒng)的高等數(shù)學(xué)教學(xué)模式中,教師是教學(xué)活動(dòng)的主體,教師對(duì)數(shù)學(xué)概念的定義與對(duì)相關(guān)定理及結(jié)論的推導(dǎo)會(huì)貫穿整個(gè)課堂教學(xué)。由于學(xué)生很少參與知識(shí)的形成過程,一直處于被動(dòng)的學(xué)習(xí)狀態(tài),所以學(xué)生學(xué)習(xí)效果差。高等數(shù)學(xué)計(jì)算機(jī)輔助教學(xué)[2-6]是計(jì)算機(jī)技術(shù)與數(shù)學(xué)軟件進(jìn)入數(shù)學(xué)教學(xué)后出現(xiàn)的一種新型教學(xué)模式,此種教學(xué)模式將先進(jìn)的計(jì)算機(jī)技術(shù)引入到數(shù)學(xué)教學(xué)過程中,借助于計(jì)算機(jī)技術(shù)將數(shù)學(xué)概念所蘊(yùn)含的數(shù)學(xué)思想及其幾何意義可視化、形象化,進(jìn)而可實(shí)現(xiàn)教學(xué)內(nèi)容的直觀化、通俗化,改善教學(xué)效果,提高教學(xué)質(zhì)量。
當(dāng)前,在高等數(shù)學(xué)計(jì)算機(jī)輔助教學(xué)中,常用的開發(fā)工具主要有PowerPoint、Flash等。這些軟件雖然都可以在不同程度上實(shí)現(xiàn)對(duì)高等數(shù)學(xué)教學(xué)內(nèi)容的輔助教學(xué)作用[2-3],但都存在比較明顯的不足。例如,軟件本身所具有的科學(xué)計(jì)算功能微乎其微;教學(xué)演示過程中無法做到對(duì)概念的準(zhǔn)確與定量的描述,且它們的主要作用都體現(xiàn)在放映效果上,缺乏與操作人員的交互性。與這些軟件不同,Matlab[7-10]是一款具有高性能的數(shù)值計(jì)算與可視化功能的軟件,它既能進(jìn)行科學(xué)計(jì)算,又具有面向?qū)ο蟮膱D形技術(shù)與GUI功能[11-12]。利用該軟件所提供GUI圖形界面編程機(jī)制,可以使開發(fā)者輕松的設(shè)計(jì)與開發(fā)出自己所需的人機(jī)交互性良好的應(yīng)用程序。近年來,伴隨著MATLAB軟件自身技術(shù)的不斷進(jìn)步及其在各領(lǐng)域的應(yīng)用,出現(xiàn)了許多利用MATLAB GUI開發(fā)的高等數(shù)學(xué)輔助教學(xué)系統(tǒng)[4-6]。這些系統(tǒng)可以起到一定的教學(xué)輔助效果,但系統(tǒng)的演示效果單調(diào)、乏味,且對(duì)概念的演示較為膚淺,對(duì)學(xué)生的直觀理解幫助很大。此外,系統(tǒng)的演示內(nèi)容也較為單薄,對(duì)于高等數(shù)學(xué)中的一些重要知識(shí)點(diǎn)并未涉及。因此,本文利用Matlab的 GUI編程,從高等數(shù)學(xué)課程的教學(xué)現(xiàn)狀出發(fā),依據(jù)高等數(shù)學(xué)課程中各重要數(shù)學(xué)概念的幾何意義及其數(shù)學(xué)思想,開發(fā)出了一種針對(duì)于高等數(shù)學(xué)各個(gè)教學(xué)模塊的輔助教學(xué)演示系統(tǒng)。與文獻(xiàn)[4-6]中的系統(tǒng)相比,本系統(tǒng)交互性良好,系統(tǒng)的設(shè)計(jì)理念與設(shè)計(jì)原則均來源于教學(xué)實(shí)踐,且演示內(nèi)容全面,演示效果生動(dòng)、深刻,能準(zhǔn)確揭示出所演示概念的本質(zhì)。
1 演示系統(tǒng)的設(shè)計(jì)與開發(fā)
在高等數(shù)學(xué)課程教學(xué)中,對(duì)各個(gè)重要數(shù)學(xué)概念的理解與掌握是最關(guān)鍵的。概念掌握了,與概念相關(guān)的其他教學(xué)內(nèi)容,包括一些定理、推論等也就不難理解了。而對(duì)于概念的理解與掌握,最關(guān)鍵的是要借助于其具體的幾何意義。基于此,本系統(tǒng)的演示對(duì)象主要針對(duì)的是高等數(shù)學(xué)課程中一些主要教學(xué)模塊所包含的重要數(shù)學(xué)概念,而系統(tǒng)的設(shè)計(jì)依據(jù)與演示內(nèi)容則為各個(gè)演示對(duì)象(即數(shù)學(xué)概念)的幾何意義。
1.1 系統(tǒng)的演示內(nèi)容
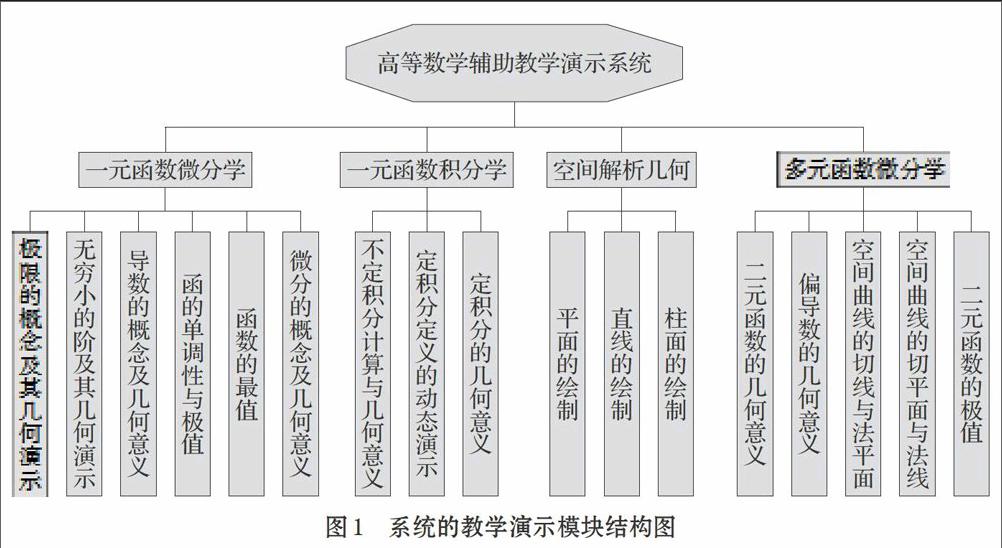
高等數(shù)學(xué)課程的教學(xué)內(nèi)容繁多,本系統(tǒng)重點(diǎn)針對(duì)四大教學(xué)內(nèi)容,分別是一元函數(shù)微分學(xué)、一元函數(shù)積分學(xué)、空間解析幾何和多元函數(shù)微分學(xué)。這四大教學(xué)內(nèi)容中,每部分都包含許多重要的數(shù)學(xué)概念,有導(dǎo)數(shù)、微分、空間曲面及偏導(dǎo)數(shù)等等。整個(gè)演示系統(tǒng)共有17個(gè)教學(xué)演示模塊,如圖1所示。
1.2 系統(tǒng)主界面的設(shè)計(jì)
系統(tǒng)主界面的設(shè)計(jì)主要是菜單欄的設(shè)計(jì)。菜單欄選項(xiàng)與圖1中系統(tǒng)各個(gè)教學(xué)演示模塊是相對(duì)應(yīng)的,其設(shè)計(jì)是通過MATLAB GUIDE所提供的菜單編輯器來實(shí)現(xiàn)的。系統(tǒng)主菜單共有6項(xiàng),其中主要菜單項(xiàng)有4項(xiàng),分別為一元函數(shù)微分學(xué)菜單項(xiàng)、一元函數(shù)積分學(xué)菜單項(xiàng)、空間解析幾何菜單項(xiàng)和多元函數(shù)微分學(xué)菜單項(xiàng)。而對(duì)于每一個(gè)主菜單項(xiàng),又會(huì)包含許多子菜單項(xiàng),這些子菜單項(xiàng)即為最終要演示的具體對(duì)象。主界面設(shè)計(jì)完成后,運(yùn)行效果如圖2所示。
2 系統(tǒng)的演示效果
本系統(tǒng)的演示模塊數(shù)量較多,由于篇幅所限,在此我們從空間解析幾何和多元函數(shù)微分學(xué)兩個(gè)主菜單中各選出一個(gè)演示模塊,來對(duì)整個(gè)系統(tǒng)的教學(xué)演示效果加以說明。
2.1 “柱面的認(rèn)識(shí)與繪制”教學(xué)模塊的演示效果
“柱面的認(rèn)識(shí)與繪制”教學(xué)演示模塊從屬于系統(tǒng)中的空間解析幾何主菜單項(xiàng)。柱面是高等數(shù)學(xué)空間解析幾何教學(xué)中的一類重要的空間幾何圖形,它有兩類基本構(gòu)成要素:一個(gè)是準(zhǔn)線,一個(gè)是母線。教材中,重點(diǎn)學(xué)習(xí)的是準(zhǔn)線在坐標(biāo)面上,母線垂直于該坐標(biāo)面的柱面。在傳統(tǒng)的板書及PPT教學(xué)方式下,部分內(nèi)容的難點(diǎn)在于,教師無法實(shí)現(xiàn)對(duì)任意給定的此類柱面的直觀繪制,這樣致使學(xué)生很難理解與認(rèn)識(shí)此類空間幾何圖形。
運(yùn)行本演示模塊,可得如圖3(a)所示界面。在界面的參數(shù)設(shè)置區(qū)中首先選擇柱面類型,這里選擇“準(zhǔn)線在xoy面,母線平行于z軸”類型,然后再輸入準(zhǔn)線函數(shù)表達(dá)式2*x^2+x-2(即準(zhǔn)線在xoy面的表達(dá)式為y=2x2+x-2),單擊“繪制圖形”按鈕,得到圖3(b)所示界面。
由以上演示過程易見,該演示模塊可實(shí)現(xiàn)對(duì)所學(xué)任意類型柱面的繪制。圖3(b)實(shí)現(xiàn)了對(duì)“準(zhǔn)線在xoy面,母線平行于z軸”類型柱面的繪制,通過改變選擇的柱面類型并修改準(zhǔn)線表達(dá)式,還可以繪制出其他類型的柱面。如圖4,此時(shí),繪制的為“準(zhǔn)線在zoy面,母線平行于x軸”且準(zhǔn)線表達(dá)式為的柱面。
2.2 二元函數(shù)偏導(dǎo)數(shù)的幾何意義教學(xué)模塊的演示效果
“二元函數(shù)偏導(dǎo)數(shù)的幾何意義”教學(xué)演示模塊從屬于系統(tǒng)中的多元函數(shù)微分學(xué)主菜單項(xiàng)。偏導(dǎo)數(shù)是多元函數(shù)微分學(xué)教學(xué)內(nèi)容中的核心概念,同時(shí),也是學(xué)習(xí)與解決多元函數(shù)全微分、多元函數(shù)極值與最值等各類問題的基礎(chǔ)。學(xué)習(xí)與掌握多元函數(shù)偏導(dǎo)數(shù)的概念關(guān)鍵是要去理解其幾何意義。眾所周知,多元函數(shù)偏導(dǎo)數(shù)的實(shí)質(zhì)為一元函數(shù)的導(dǎo)數(shù),因此,其幾何意義仍為曲線在某點(diǎn)處切線的斜率。以二元函數(shù)z=f(x,y)為例,其在點(diǎn)(x0,y0)處對(duì)x偏導(dǎo)fx(x0,y0)的幾何意義為曲面z=f(x,y)與平面y=y0的交線在點(diǎn)(x0,y0,f(x0,y0))處切線的斜率;其在點(diǎn)(x0,y0)處對(duì)y偏導(dǎo)fy(x0,y0)的幾何意義則為曲面z=f(x,y)與平面x=x0的交線在點(diǎn)(x0,y0,f(x0,y0))處切線的斜率。在傳統(tǒng)的板書教學(xué)與PPT演示教學(xué)中,此部分教學(xué)內(nèi)容的難點(diǎn)在于教師不能夠靈活、直觀、準(zhǔn)確地繪制出任意所給定的二元函數(shù)z=f(x,y)所表示的曲面與相應(yīng)平面的交線,這樣,致使學(xué)生對(duì)于其幾何意義的認(rèn)識(shí)不直觀、不深刻。
運(yùn)行該模塊,可得如圖5(a)所示界面。在該界面中,當(dāng)在參數(shù)設(shè)置區(qū)內(nèi)輸入二元函數(shù)的表達(dá)式f(x,y)及(x0,y0)點(diǎn)的具體值并選擇求偏導(dǎo)的類型后,當(dāng)點(diǎn)擊“計(jì)算偏導(dǎo)”按鈕,可以計(jì)算出輸入的二元函數(shù)在輸入點(diǎn)(x0,y0)處關(guān)于選定的偏導(dǎo)的類型的偏導(dǎo)數(shù)。之后,當(dāng)點(diǎn)擊“演示幾何意義”按鈕,可形象直觀地繪制出相應(yīng)計(jì)算出的偏導(dǎo)數(shù)的幾何意義。例如,當(dāng)輸入的二元函數(shù)為2*x^2+x*y^2+x*y(即書面中的函數(shù)2x2+xy2+xy),x0為1,y0為1,選擇求偏導(dǎo)類型為“對(duì)x求偏導(dǎo)”,點(diǎn)擊“計(jì)算偏導(dǎo)”按鈕,之后,點(diǎn)擊“計(jì)算偏導(dǎo)”按鈕,可形象直觀地繪制出其幾何意義,如圖5(b)。
由圖5(b)易見,該演示模塊可實(shí)現(xiàn)對(duì)所輸入的任意二元函數(shù)在任意點(diǎn)(x0,y0)處的偏導(dǎo)數(shù)。本例中,求得的f(x,y)在點(diǎn)(1,1)處對(duì)自變量x的偏導(dǎo)值fx(1,1)為6。除此以外,該演示模塊最大的優(yōu)勢(shì)在于可以直觀、生動(dòng)的演示出fx(1,1)的幾何意義。由圖5(b),易知,該演示模塊界面左側(cè)的空間直角坐標(biāo)系中可顯示出此時(shí)曲面z=2x2+xy2+xy與平面y=1的交線;而與此同時(shí),為了更直觀的來理解fx(1,1)的幾何意義,演示模塊界面右側(cè),則將該交線從空間直角坐標(biāo)系中分離出來,將其放置在平面y=1內(nèi)部的平面直角坐標(biāo)系(該坐標(biāo)系橫軸為x軸縱軸為z軸)內(nèi),此時(shí)該平面曲線在點(diǎn)(1,4)的切線(即圖5(b)中右側(cè)坐標(biāo)系中紅色的切線)的斜率即為fx(1,1)的幾何意義。當(dāng)然,通過改變偏導(dǎo)的類型,選擇“對(duì)y求偏導(dǎo)”,也可以類似的獲得f(x,y)在點(diǎn)(1,1)處對(duì)自變量y的偏導(dǎo)值fy(1,1)及其幾何意義。
3 結(jié)束語
本文中所研發(fā)的基于MATLAB GUI的高等數(shù)學(xué)輔助教學(xué)演示系統(tǒng),人機(jī)交互性良好,演示內(nèi)容全面,演示手段豐富且演示效果生動(dòng)、深刻,能準(zhǔn)確的揭示出所演示數(shù)學(xué)概念的本質(zhì),因而,更能貼近于教學(xué)實(shí)踐。從實(shí)踐教學(xué)活動(dòng)中的應(yīng)用來看,學(xué)生對(duì)系統(tǒng)的交互性使用及其演示效果均較為滿意。下一步,計(jì)劃將高等數(shù)學(xué)中一些更為復(fù)雜的教學(xué)模塊(包括多元函數(shù)積分學(xué)及級(jí)數(shù)等)引入到模塊中來,從而實(shí)現(xiàn)對(duì)整個(gè)高等數(shù)學(xué)課程知識(shí)點(diǎn)的全覆蓋。
參考文獻(xiàn)(References):
[1] 同濟(jì)大學(xué)數(shù)學(xué)系.高等數(shù)學(xué)[M].高等教育出版社,2007.
[2] 薛春明.高等數(shù)學(xué)多媒體輔助教學(xué)的幾點(diǎn)思考[J].科技信息,2010.19:156
[3] 崔楠.Power point在制作CAI 課件中的應(yīng)用與技巧[J].計(jì)算機(jī)時(shí)代,2001.1:3
[4] 時(shí)紅霞.高等數(shù)學(xué)實(shí)驗(yàn)教學(xué)的應(yīng)用研究[D].西安建筑科技大學(xué)碩士學(xué)位論文,2006.
[5] 崔秋珍.基于MATLAB的高等數(shù)學(xué)試驗(yàn)系統(tǒng)設(shè)計(jì)與圖形界面系統(tǒng)實(shí)現(xiàn)[D].西安建筑科技大學(xué)碩士學(xué)位論文,2006.
[6] 許仨.高等數(shù)學(xué)多媒體教學(xué)系統(tǒng)的設(shè)計(jì)與實(shí)現(xiàn)[D].貴州大學(xué),2010.
[7] 胡曉冬,董辰輝.MATLAB從入門到精通[M].人民郵電出版社,2010.
[8] 陳杰.MATLAB寶典[M].電子工業(yè)出版社,2007.
[9] 葛哲學(xué).精通MATLAB[M].電子工業(yè)出版社,2008.
[10] 張志涌,楊祖櫻.MATLAB教程[M].北京航空航天大學(xué)出版社出版,2015.
[11] 羅華飛.MATLAB GUI設(shè)計(jì)學(xué)習(xí)手記[M].北京航空航天大學(xué)出版社出版,2014.
[12] 陳垚光,毛濤等.精通MATLAB GUI設(shè)計(jì)[M].電子工業(yè)出版社,2013.

