基于AQWA的大型游船碼頭系泊水動力性能分析

雷林+劉添宇+袁培銀+劉俊良

摘 要：隨著世界經濟的不斷發展，航行船舶增加，大型船舶碼頭系泊的安全性越來越受到人們關注。本文基于三維勢流理論，運用ANSYS軟件AQWA模塊，對碼頭系泊時大型游船進行頻域分析和時域分析，得到一系列參數和運動規律。研究結果和研究方法可為同類船舶碼頭系泊提供參考。

關鍵詞：AQWA；碼頭系泊；頻域分析；時域分析

中圖分類號：U656.1 文獻標識碼：A 文章編號：1006—7973（2017）05-0041-04

隨著世界經濟的不斷發展，人們收入的不斷增加，海上旅游業不斷興旺，旅游船隊的規模不斷地增大，內河與海上的旅游觀光人數越來越多，乃至到現在，海上旅游已經成為了歐洲以及亞洲人的一種時尚。在豪華游輪發展的同時，其系泊系統在安全中占據了比較重要的一部分，豪華游輪的系泊系統是船舶停靠和港口設計需要考慮的重要問題之一。國內對于船舶碼頭系泊的研究相對較晚，始于20世紀年代90后期，主要采用了物理模型試驗、數值模擬的方法對影響船舶系纜力的海洋動力因素、船舶因素進行了相關研究。

本文應用多體水動力學軟件 AQWA，針對碼頭與大型游船組成的靠幫系泊系統，基于三維勢流理論，在考慮船和碼頭間水動力相互作用的情況下，計算靠幫系泊時船舶所受到的波浪載荷，并與不考慮船和碼頭水動力相互作用的計算結果進行對比分析。

1 計算流程及理論基礎

本文采用ANSYS中的AQWA模塊進行計算，首先通過ANSYS軟件進行建模，然后生成DAT文件，導入AQWA中進行水動力分析。

2 大型游船碼頭系泊系統模型

2.1 大型游船主尺度參數

碼頭系泊游船的主尺度參數如表1所示。碼頭的主尺度參數如表2所示。根據游船船型值建立船體和碼頭面域模型并劃分網格，船舶及碼頭示意圖如圖1所示。

2.2 碼頭系泊纜及護舷布置

本文研究的對象游船碼頭系泊共有8根系纜繩，其中船艏纜和船尾纜各兩根，船中橫纜四根交叉進行系泊。

護舷采用漂浮型橡膠護舷，設計反力1872kN 最大反力1992kN。纜繩和護舷布置形式如圖2所示。

2.3 環境載荷

表3給出了游船在系泊時主要環境參數，包括風浪流的具體參數。

3 大型游船的水動力性能分析

3.1 頻域分析結果

此次頻域計算分析給出了船舶在單獨停靠下和在碼頭停靠下兩種工況下的六自由度的RAO（幅值響應算子）。

由以上圖像分析可以看出，船舶的運動周期為26s，碼頭對船舶六自由度上的RAOS影響是不一樣的。可以得出以下結論：

（1）由圖3和圖5可見，在縱蕩、垂蕩方面，單獨船舶運動隨著時間增加一直呈上升趨勢，到了30s時，分別有最大的幅值3.0和0.8，加入了碼頭之后，也是呈上升趨勢，最大幅值分別為為6.0和1.4，可見碼頭對船舶的縱蕩和垂蕩運動的RAO起到了一定的增幅作用。

（2）由圖4可見，在橫蕩方面，單獨船舶橫蕩隨時間增加一直成上升趨勢，加入了碼頭之后，也呈上升趨勢，可見碼頭可以減小橫蕩下船舶的運動的RAO。

（3）由圖6和圖8可見，在橫搖、艏搖方面，單獨船舶運動隨著時間增加出現上下波動，加入了碼頭之后，運動趨勢大體不變，但從運動幅值可以看出碼頭能減小船舶橫搖和艏搖下的運動的RAO。

（4）由圖7可見，在縱搖方面，單獨船舶橫搖隨時間增加出現先增加后下降的趨勢，加入碼頭之后，運動趨勢大體不變，但是從運動幅值可以看出碼頭對船舶的縱搖運動的RAO有一定的增幅作用。

3.2 時域分析結果

3.2.1 六自由度運動響應

AQWA-DRIFT模塊模擬計算在給定的環境載荷下碼頭系泊系統3個小時（步長0.2s，共54000步）的運動情況。最終得到碼頭系泊下船舶的總體運動響應，系泊纜張力和護舷壓力的時歷變化曲線。

由以上圖像可得出以下結論：

（1）由圖9可以看出，在風浪流載荷下，船舶在三個方向上的運動頻率差別較大，其中垂向上運動頻率最大，但是運動幅值最小，最大變化幅值為0.1m；橫向上由于受到纜繩和護舷的作用最大，運動頻率最小，運動周期最大，運動幅值也相對比較大，最大變化幅值為2m；而縱向方向上，受到纜繩和護舷的作用相對比橫向方向小，所以運動頻率和運動幅值相對居中，最大運動幅值為0.8m。

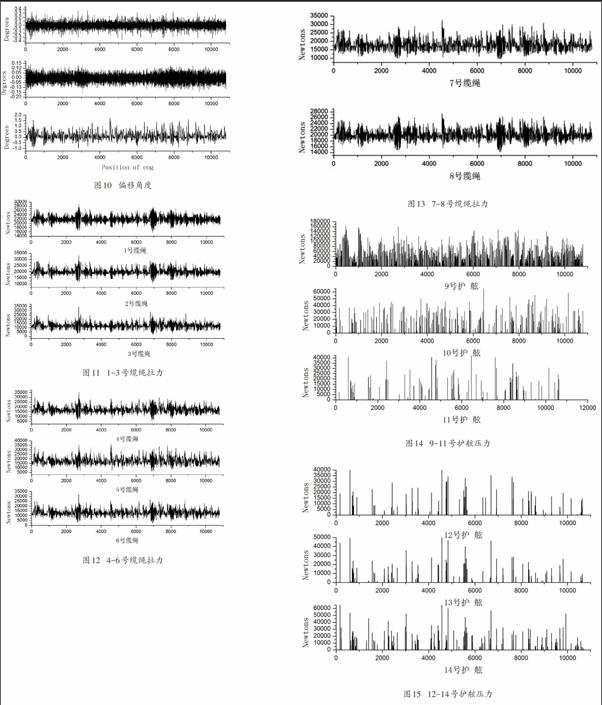
（2）由圖10可以看出，在風浪流載荷下，橫搖運動頻率最大，運動幅值最小，最大變化幅值為0.3度；艏搖運動頻率最小，運動幅值最大，最大變化幅值為2.5度；縱搖運動頻率也比較大，相對橫搖較小，相對艏搖較小，運動幅值也比較居中，最大變化幅值為0.7度。

3.2.2 系纜張力

圖11到圖13給出了8根系泊纜隨時間變化曲線。由圖像可以看出，所有的纜繩運動頻率大致相同。其中3號纜繩到6號纜繩張力相對較大，8號纜繩張力較小，1號纜繩和2號纜繩張力比較接近，5號纜繩極值最大，為39.22KN，8號纜繩極值最小26.3KN。

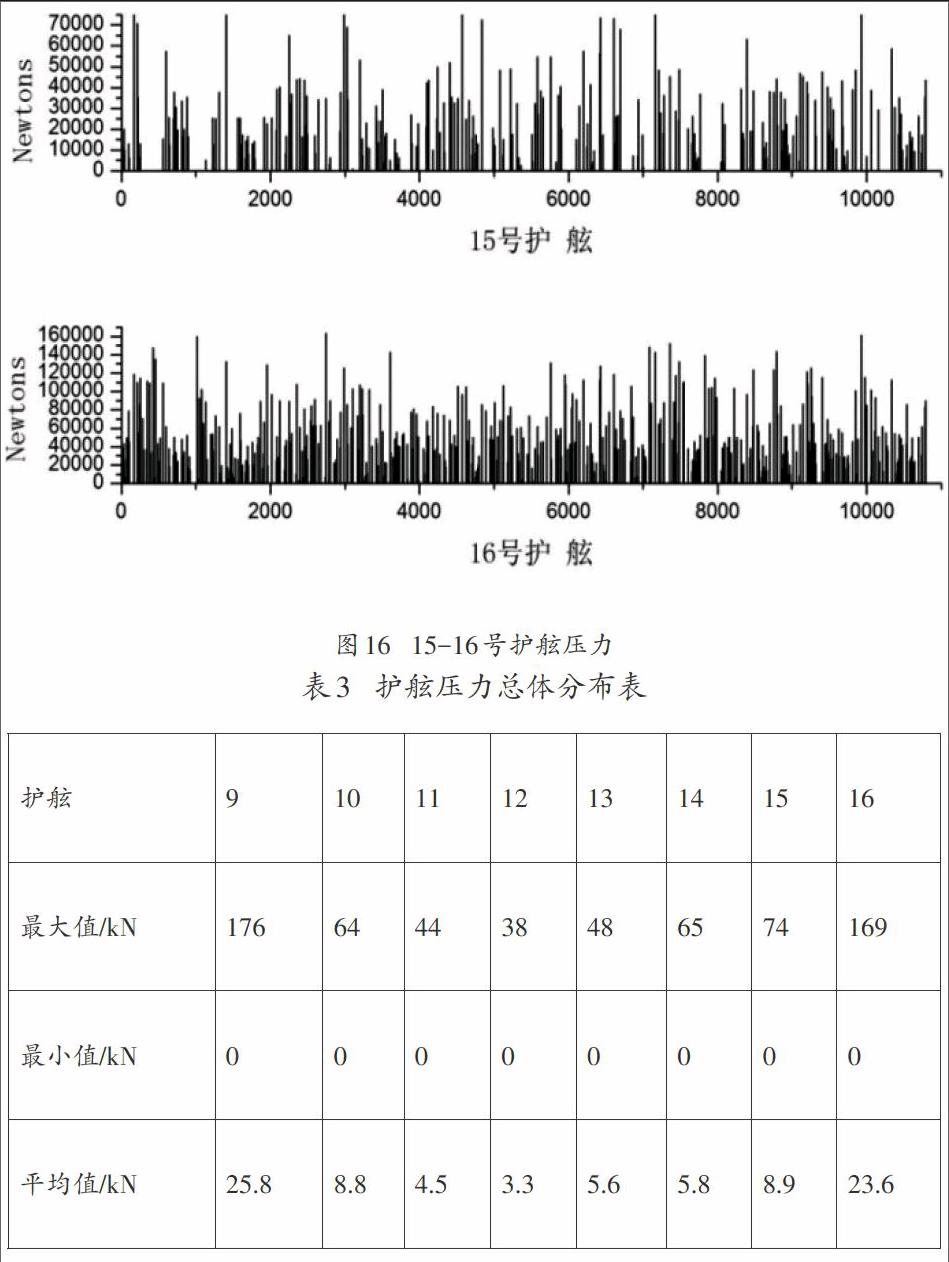
3.2.3 護舷壓力

圖14到圖16給出了風浪流載荷下碼頭護舷壓力的變化情況。由圖可以看出，首尾兩端的護舷所承受的壓力最大。這是因為從前面船舶的運動響應可以看出，船舶艏搖的運動最為劇烈，最大達到了2.5度，導致船舶首尾兩端所承受的壓力最大。所以在首尾兩端護舷應采取相關有效保護措施。

4 結語

本文以某大型游船為例，應用多體水動力軟件AQWA，模擬船舶在碼頭系泊情況，分別從頻域和時域兩個方面對船舶水動力特性進行分析，得到各頻域時域曲線圖，從中得出以下結論：

（1）在頻域中，碼頭能對船舶的縱蕩，垂蕩，縱搖運動起到一定的增幅作用，能減小船舶在橫蕩，橫搖，艏搖下的運動。

（2）在時域中，船舶在風浪流聯合作用下，始終在垂向方向上的運動頻率最大，運動幅值最小；在橫向上運動頻率最小，運動幅值最大；在縱向上運動頻率和運動幅值相對與橫向和垂向處于居中的地位。

（3）系泊纜張力方面，由于首尾纜長度較長，拉力比中間橫纜的拉力大，拉力最大是5號纜繩，最小是8號纜繩。

（4）護舷壓力方面，由于艏搖較為劇烈，所以首尾部承受撞擊載荷最大，護舷壓力也就最大。

參考文獻：

[1]向溢等.碼頭系泊纜繩張力的蒙特卡洛算法[J].上海交通大學學報.2001.35（4）.

to the spillway. The mooring line tension of the Monte Carlo algorithm[J]. Journal of Shanghai Jiao TongUniversity.2001.35 （4）.

[2]向溢等.碼頭系泊船舶纜繩張力的混沌解法[J].上海交通大學學報.2001.25（1）.

to the spillway. The mooring ship's cable tension chaos for [J]..2001.25 Journal of Shanghai Jiao Tong University （1）.

[3]鄒志利.港口內靠碼頭系泊船運動的計算[J].海洋工程，1995.第3期：25-36.

Zou Zhili. Calculation of berthing ship berthing in port [J]. MarineJiao Tong University （1）.

[4]張鼎，黃唯.大型集裝箱船碼頭系泊及抗臺風計算分析[J].船舶與海洋工程，2014.第二期.15-19.

Zhang Ding， Huang Wei. Calculation and analysis of mooring and typhoon resistance of large container ships [J]. ship and ocean engineering， 2014，.15-19.， second

[5]胡翼，胡紫劍，劉元丹，劉敬喜.基于AQWA的大型LNG船碼頭系泊分析[J]. 艦船科學技，2012.34（2）.70-73

Hu wing， Hu Zijian， Liu Yuandan， et al. Mooring analysis of large scale LNG ship dock based on [J]. AQWA ship science and technology， 2012.34 （2）.70-73

[6]向溢，譚家華，楊建民.碼頭系泊船舶模型試驗[J].海洋工程，2001.19（2），46-49

Xiang Yu， Tan Jiahua， Yang Jianmin. Mooring mooring model test of [J]. marine engineering， 2001.19 （2）， 46-49

[7]于洋，洪碧光.碼頭系泊船水動力特性的研究[J].大連海事大學學報，1996.25（3）.36-38

Yu Yang， Biguang Hong. Study on dynamic characteristics of mooring ship water [J]. Journal of Dalian Maritime University， 1996.25 （3）.36-38

[8]吳小鵬.深海半潛式鉆井平臺碼頭系泊數值計算與模型試驗研究[D].上海交通大學碩士論文.2010

Wu Xiaopeng. Numerical calculation and model test of mooring for deepwater semi submersible drilling platform [D]..2010， master thesis，Shanghai Jiao Tong University

基金項目：

重慶市社會民生科技創新專項資助項目（CSTC2015shmszx30021）

重慶市社會民生科技創新專項資助項目（CSTC2015shmszx30011）

重慶市教委科學技術研究項目（KJ1600536）