基于等效模型和多時間尺度擴展卡爾曼濾波的鋰離子電池SOC預測

陳 冰, 魯 剛, 房紅征, 張明敏

(1.海軍工程大學 電子工程學院，武漢 430033；2.海軍裝備部, 北京 100055；3.北京航天測控技術有限公司，北京 100041；4.北京市高速交通工具智能診斷與健康管理重點實驗室，北京 100041)

基于等效模型和多時間尺度擴展卡爾曼濾波的鋰離子電池SOC預測

陳 冰1, 魯 剛2, 房紅征3,4, 張明敏1

(1.海軍工程大學 電子工程學院，武漢 430033；2.海軍裝備部, 北京 100055；3.北京航天測控技術有限公司，北京 100041；4.北京市高速交通工具智能診斷與健康管理重點實驗室，北京 100041)

荷電狀態(SOC)和最大可用電量估計是鋰離子電池壽命預測中的兩個最重要部分；然而與快速時變的SOC比較，最大可用電量的參數變化緩慢；文章提出了一個基于等效模型和多時間尺度的擴展卡爾曼濾波(EKF)預測算法對SOC和最大可用容量分別在不同時間尺度上進行估計，在宏觀尺度上利用了SOC估計值作為觀測量，更新最大可用電量；針對NCA/C衛星鋰離子電池實驗數據的仿真結果表明，提出的多時間尺度EKF預測算法與EKF聯合估計算法相比，SOC和最大可用電量估計準確度更高，同時提高了計算效率。

SOC; 最大可用電量; Thevenin等效電路模型; 多時間尺度；EKF預測算法

0 引言

鋰離子電池對衛星電源系統至關重要，正在逐步替代傳統電池成為第三代衛星用儲能電源[1]。由于鋰電池自身存在充放電管理、性能衰退等問題，對其工作狀態監測、性能退化分析和剩余壽命(RUL)預測等已經成為衛星系統故障預測和健康管理(PHM)領域研究的關鍵[2-4]。

電池的最大可用電量常被用作電池壽命的退化特征。準確的SOC估計不僅能用來評估設備的可靠性，還能反映電池的剩余使用壽命等關鍵信息。除了傳統的開路電壓法、安時積分法等，文獻[5-7]對Kalman濾波方法應用于衛星鋰電池的SOC估計進行了詳細的分析。文獻[8]改進了擴展卡爾曼(EKF)算法，先利用狀態量和方差矩陣構造Sigma點集，這種基于Sigma點的Kalman濾波算法可以取得更好的精度。文獻[9]將Kalman濾波算法與安時積分法結合。文獻[10]使用無損卡爾曼濾波對鋰電池SOC進行預測。文獻[11]提出的EKF聯合估計算法能夠進行具有噪聲電壓和電流測量的實時SOC和最大可用電量估計。

目前采用狀態與參數聯合估計技術的最大可用電量估計的準確性較差。原因有兩點：一是電池端電壓是唯一測量數據，但是最大可用電量與電池電壓之間的聯系非常弱；另外由于SOC和最大可用電量之間的強相關性，不準確的最大可用電量估計將會進一步導致不準確的SOC估計，反之亦然。在計算效率方面，最大可用電量是指示系統健康狀態(SOH)的緩慢時變量，如果最大可用電量估計與快速時變量SOC在相同的時間尺度上執行，將導致高計算復雜性。為了解決這些困難，本文提出了一種基于等效電路模型和多時間尺度EKF預測算法對SOC和最大可用電量分別進行估計，貢獻主要有：(1)設計了多時間尺度的SOC和最大可用電量的時間尺度分離估計算法；(2)采用SOC估計值動態更新最大可用電量的預測值。作為一種安時積分法和EKF濾波混合的技術，該算法實現了比EKF聯合估計算法更高的精度和效率。

1 衛星鋰離子電池等效電路模型和多時間尺度離散化模型

1.1 Thevenin等效電路模型

衛星鋰離子電池的等效電路模型有Rint模型，RC模型，Thevenin模型和PNGV模型[6]等。Thevenin等效電路模型[12]考慮了電池電壓在電流激勵下的突變和漸變，結構見圖1。該模型參數描述如下：Uoc表示電池的開路電壓(OCV)；Rt用于描述電池歐姆電阻在雙電層中的電荷的累積和耗散；Rp表示電池極化電阻，Cp表示電池極化電容，它們構成的RC網絡用于模擬衛星鋰電池在極化現象的產生和消除過程中所表現出的動態特性；Up表示RC網絡上的極化電壓；U表示電池的端電壓；I表示電池負載電流(假定放電為正，充電為負)。

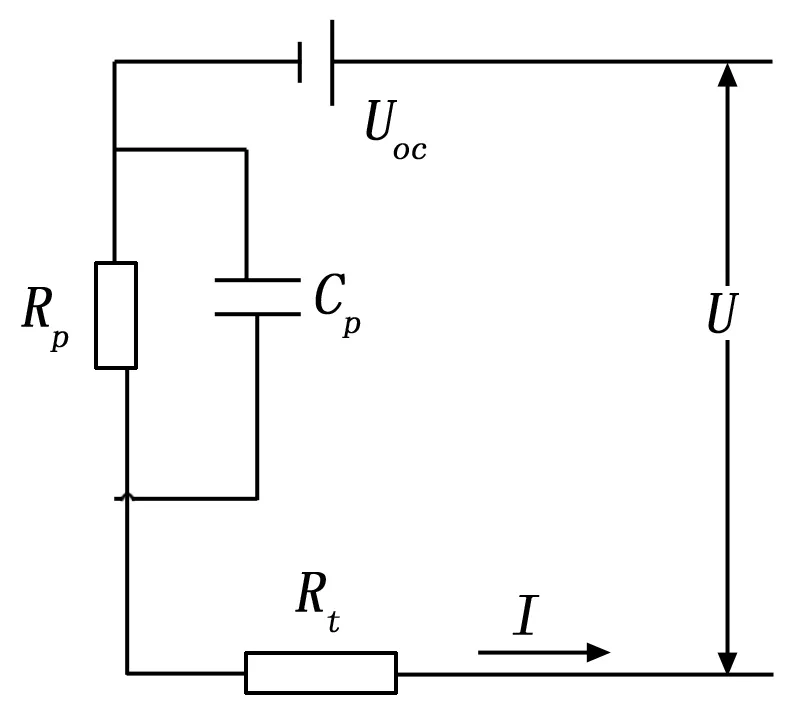
圖1 鋰離子電池Thevenin等效電路模型

SOC

定義為可用電量與額定電量的比值，相當于鋰電池的電量計。環境溫度確定時，

OCV

與

SOC

間關系是鋰電池的靜態特性的反映

[13]

，并且是可辨識的。

令z=SOC，此處使用f(z)來描述OCV與SOC之間這種確定關系。需要指出的是，電池SOC與其端電壓的聯系已經通過f(z)增強，這對于提高SOC預測精度非常重要。由圖可知Thevenin模型各參數數學關系式可以表述為：

U=Uoc-Up-IRt=f(z)-Up-IRt

(1)

(2)

安時積分法是最簡單的SOC估計方法，也是目前應用較多的SOC估計算法。它通過對運行時間內流過電池的電流進行積分，計算流入或者流出電池的電量，如果己知電池的初始SOC值，便可用初始SOC值加上或減去流過電池的電量，得到電池剩余電量公式(3)是得到SOC狀態方程的基礎：

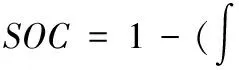
i·η·dt)/Q

(3)

其中i為電流，Q為電池最大可用電量，t為時間，(為庫倫有效因子，定義為恢復到最初電量所需充電和放電能量的比值。(小于或等于1。例如，在放電模式中，當達到最小放電電壓時，認為電池已經完全放電，則SOC為0。通過Thevenin等效電路模型與安時積分法的結合，將電池參數和SOC與其端電壓聯系起來。以荷電狀態SOC、極化電壓Up為狀態變量，得到狀態方程為：

(4)

以端電壓U為量測值，則觀測方程為：

U=f(z)-Up-IRt

(5)

1.2 多時間尺度的離散化模型

EKF應用對象是非線性離散系統，因而需要對上節提出的連續模型離散化。對于參數變化快慢差別很大的系統，我們可以設置兩個時標：宏觀時標和微觀時標。處于宏觀時標中的系統量往往隨著時間變化而緩慢變化，而微觀時標上則表現為系統量隨著時間快速變化。

為了方便表述，分別使用k和l作為宏觀時間尺度和微觀時間尺度的時間指標。任意時刻均可以表示為tk,l，并且存在這樣的關系：tk,l=tk,0+l·T，tk,0=tk-1,L(l=1,2,...,L；k=1,2,...,∞)，T是兩個相鄰測量點之間的固定時間間隔。值得注意的是，L代表時標分離的水平。根據系統參數的變化情況，確定宏觀時間尺度的宏觀仿真時間步數k；在k與k+1時間步之間，根據系統狀態量的變化情況，確定采樣周期T，即得到宏觀仿真時間步數l。考慮到模型參數是慢時變的，因而假設電池是時不變系統，并且負載電流在每個采樣間隔T內保持恒定，進而可以得到方程(2)的解析解，如下所示：

(6)

圖1所示電池模型以荷電狀態z、極化電壓Up為狀態變量，負載電流I為輸入量，端電壓U為輸出量，在多時間尺度上離散化后得到：

(7)

令zk,l=SOC，由式(3)得到：

(8)

令τp=Rp·Cp，由式(4)到式(8)可以得到：

(9)

多時間尺度上的離散化狀態轉移和測量方程為：

(10)

為了使接下來的討論更具有一般性，將式(10)改寫為以下非線性狀態空間模型：

傳遞：xk,l+1=F(xk,l,uk,l,θk)+wk,l,θk+1=θk+rk

測量：yk,l=G(xk,l,uk,l,θk)+vk,l

(11)

其中，xk,l是在時間為tk,l=tk,0+l·T，l=1,2,...,L時的系統狀態矢量，T是兩個相鄰測量點之間的固定時間間隔，k,l表示宏觀和微觀時標的序號。值得注意的是，L代表時標分離的水平，且xk,0=xk-1,L。θk是時間為tk,0時系統模型參數的矢量；uk,l是外部觀測源的輸入；yk,l是系統觀察值(或者量測值)的矢量。wk,l和rk分別是狀態和模型參數的過程噪聲矢量；vk,l是測量噪聲的矢量；F()和G()分別是狀態傳遞和狀態測量函數。

2 多時間尺度的EKF預測算法

針對系統在多時間尺度上的離散模型，使用多時間尺度的EKF預測算法來預測SOC與最大可用容量。多時間尺度算法預測過程共分為六步，宏觀EKF和微觀EKF一起以嵌套循環的形式執行。在每個宏觀時間步k內，宏觀EKF進行時間更新、狀態預測和測量更新。每個微觀時間步l內，微觀EKF執行時間更新和測量更新。當l=1循環到l=L時，該宏觀時間步k結束，進入下一個宏觀時間步k+1。無論宏觀或微觀EKF，開始執行前均需要通過把基于先驗信息的經驗值賦予模型參數θ和狀態x來進行初始化。估計誤差的協方差矩陣∑θ和∑x也根據先驗信息進行初始化。基本步驟總結如下：

第一步：初始化。

(12)

在宏觀尺度 上：

第二步：宏觀EKF的時間更新。

(13)

第三步：宏觀EKF的狀態預測。

(14)

第四步：宏觀EKF的測量更新。

(15)

(16)

在微觀尺度上如下。

第五步：微觀EKF的時間更新。

(17)

第六步：微觀EKF的測量更新。

(18)

= (I-Kk,lxCk,lx)∑xk,l-

(19)

其中，定義以下Yacobi矩陣：

(20)

(21)

接下來介紹衛星鋰電池系統多時間尺度的EKF預測算法執行過程。流程圖見圖2。算法包括兩個并行運行的擴展式卡爾曼濾波器：上半部分(微觀EKF)在微觀時標上修正SOC，下半部分(宏觀EKF)在宏觀時標上修正可用電量。微觀EKF發送SOC估計值到宏觀EKF并從宏觀EKF接收最大可用電量估計值。

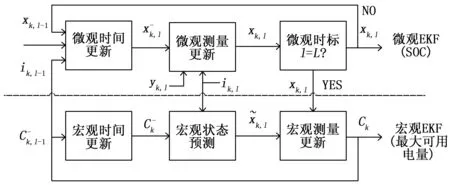
圖2 基于EKF的衛星鋰電池SOC多時間尺度估算流程圖

3 實例驗證

3.1 實驗過程

實驗采用了最大可用電量為1.6Ah的NCA/C星載鋰離子電池。測試系統包括衛星鋰電池綜合測試設備、溫度傳感器組件、NCA/C星載鋰電池以及專用安裝夾具等。根據本地試驗效果用37號電池的數據進行辨識和仿真。實驗所用的NCA/C星載衛星鋰電池及實驗設備見圖3。

圖3 衛星鋰離子電池及實驗設備

3.2 實驗結果及分析

在MATLAB軟件中建立Thevenin等效電路模型，自定義工況電流作為輸入信號，進行仿真實驗。使用EKF聯合估計算法[13]得到的SOC以及最大可用電量估計曲線如圖4所示。

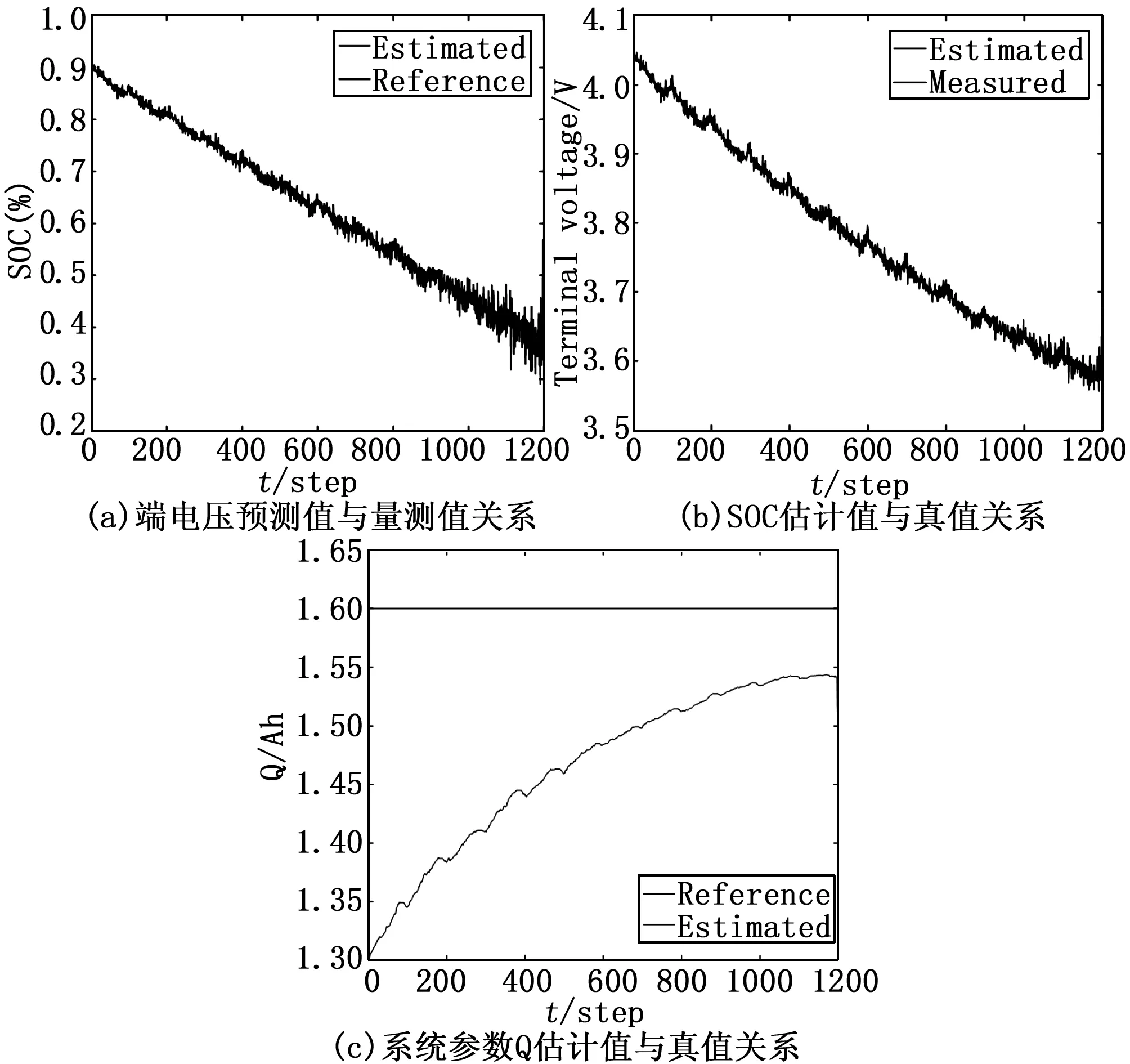
圖4 EKF聯合估計算法仿真結果

使用多時間尺度的EKF預測算法得到的NCA/C星載鋰電池SOC以及最大可用電量估計曲線如圖5所示。

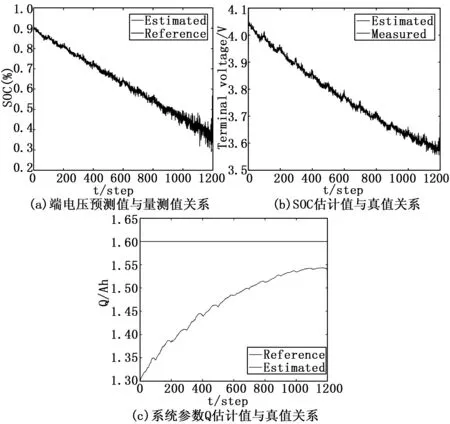
圖5 多時間尺度算法仿真結果

關于最大可用電量估計，兩種方法設置的初始值均小于真實值，見圖4(c)和圖5(c)。從圖4(c)可以明顯看出估計最大可用電量未能密切跟蹤真實最大可用電量，最終收斂到真實最大可用電量大約4.3%的誤差范圍內，且包含較大的噪聲。而圖5(c)隨著仿真步數增加逐漸收斂到真實最大可用電量。EKF聯合估計算法的精度較低歸因于在SOC和最大可用電量估計方面的測量和時間尺度耦合。為修正最大可用電量預測值，EKF聯合估計算法使用電池端電壓作為量測值對最大可用電量進行修正，見公式(22)。

(22)

不同的是，多時間尺度算法在宏觀尺度上按照公式(23)和(24)對最大可用電量進行估計，避免了并行的SOC和最大可用電量估計過程僅依賴于量測值(電池端電壓)。

(23)

(24)

除準確性比較外，在計算效率方面也比較了兩種方法，如表1所示。

表1 計算效率對比

為將隨機性的影響減到最小，將上述兩種方法執行了10次，取均值進行比較。表1總結了平均計算的時間，可以觀察到多時間尺度的EKF預測算法比EKF聯合估計算法消耗了較少的計算時間。這有助于在衛星故障預測和健康管理(PHM)系統中減少計算量以及硬件的負擔，有利于提高PHM系統應用靈活性和效率。

4 結論

多時間尺度的EKF預測算法是針對時標分離的工程系統有效的、準確的狀態及參數估計方法。本文基于等效模型，利用多時間尺度EKF算法在微觀尺度上對鋰離子電池SOC進行預測，并在宏觀尺度上利用了SOC估計值作為觀測量對最大可用電量進行預測，效果優于EKF聯合估計，同時提高了計算效率。下一步工作將在建立鋰離子電池的等效模型以及OCV與SOC關系模型時，考慮溫度對SOC的影響、電量對OCV的影響等，提高模型精度以獲得更準確的估計值。

[1] 吳宇平, 萬春榮, 姜長印. 鋰離子二次電池[M].北京：化學工業出版社, 2002.

[2] 艾 力, 房紅征, 于功敬，等. 基于數據驅動的衛星鋰離子電池壽命預測方法[J]. 計算機測量與控制, 2015, 23(4):1262-1265; 1272.

[3] 陳 冰, 魯 剛, 房紅征，等. 基于最小二乘支持向量機的衛星異常檢測方法[J]. 計算機測量與控制, 2014, 22(3):690-692.

[4]GoebelKai,etal.Prognosticsinbatteryhealthmanagement[J].IEEEinstrumentation&measurementmagazine[J].2008，11(4)： 33-40.

[5]PlettGregoryL.ExtendedKalmanfilteringforbatterymanagementsystemsofLiPB-basedHEVbatterypacks:Part1.Background[J].JournalofPowerSources，2006(2):262-276.

[6]PlettGregoryL.ExtendedKalmanfilteringforbatterymanagementsystemsofLiPB-basedHEVbatterypacks:Part2.Modelingandidentification[J].Journalofpowersources，2004(2): 262-276.

[7]PlettGregoryL.ExtendedKalmanfilteringforbatterymanagementsystemsofLiPB-basedHEVbatterypacks:Part3.Stateandparameterestimation[J].JournalofPowersources，2004(2): 277-292.[8]PlettGregoryL.Sigma-pointKalmanfilteringforbatterymanagementsystemsofLiPB-basedHEVbatterypacks:Part1:Introductionandstateestimation[J].JournalofPowerSources，2006(2): 1356-1368.[9] 胡運飛. 混合動力汽車用鎳氫電池建模及其SOC估計研究[R]. 中國科學院電工研究所, 2008.

[10]HeWei,etal.StateofchargeestimationforLi-ionbatteriesusingneuralnetworkmodelingandunscentedKalmanfilter-basederrorcancellation[J].InternationalJournalofElectricalPower&EnergySystems，2014，62: 783-791.

[11]LeeSeongjun,etal.State-of-chargeandcapacityestimationoflithium-ionbatteryusinganewopen-circuitvoltageversusstate-of-charge[J].Journalofpowersources，2008(2): 1367-1373.

[12]Rahimi-Eichi,BarontiHF,ChowMY.ModelingandonlineparameteridentificationofLi-PolymerbatterycellsforSOCestimation[C].IndustrialElectronics(ISIE), 2012IEEEInternationalSymposiumon.IEEE, 2012.

[13]SimonD.Optimalstateestimation:Kalman,H-infinity,andnonlinearapproaches[M].JohnWiley&Sons, 2006.

SOC Prediction of Lithium-ion Batteries Based on Equivalent Circuit model and Multi-time Scale Extended Kalman Filter

Chen Bing1, Lu Gang2, Fang Hongzheng3,4, Zhang Mingmin1

(1.College of Electronic Engineering, Naval University of Engineering, Wuhan 430033, China; 2.Equipment Department of Navy, Beijing 100055, China; 3.Beijing Aerospace Measure & Control Corp. Ltd.Beijing 100041, China; 4.Beijing Key Laboratory of High-speed Transport Intelligent Diagnostic and Health Management, Beijing 100041, China)

The state of charge (SOC) and the maximum available electricity estimation are two of the most important parts of satellite lithium-ion battery life prediction. However, compared with the fast time-varying SOC, the parameters of the maximum available power change slowly. It proposed a multi-time scale extended Kalman filter (EKF) prediction algorithm based-on the equivalent circuit model to estimate the SOC and the maximum available capacity at different time scales. The SOC estimation is used as an observation on the macroscopic scale to update the maximum available power. The simulation results of NCA/C lithium-ion battery show that the proposed multi-time scale EKF prediction algorithm has higher accuracy of SOC and maximum available power estimation compared with tradtional EKF algorithm, and improves the computational efficiency.

SOC; maximum available electricity; Thevenin equivalent circuit model； multi-time scale； EKF；prediction algorithm

2017-03-10；

2017-03-17。

陳 冰(1979-)，女，黑龍江哈爾濱人，副教授，主要從事裝備維修保障技術方向的研究。

1671-4598(2017)05-0067-04

10.16526/j.cnki.11-4762/tp.2017.05.019

TP277; V57

A