一種提高軌道精度的改進姿態(tài)控制技術(shù)

李 君,程 興,陳 宇 ,張普卓,董朝陽

(1.北京航天航天大學 航空工程學院，北京 100191; 2.北京宇航系統(tǒng)工程研究所，北京 100072)

一種提高軌道精度的改進姿態(tài)控制技術(shù)

李 君1，2,程 興2,陳 宇2,張普卓2,董朝陽1

(1.北京航天航天大學 航空工程學院，北京 100191; 2.北京宇航系統(tǒng)工程研究所，北京 100072)

針對我國長征系列火箭普遍存在的殘骸落點普遍較理論落點靠前的現(xiàn)象，開展多次飛行數(shù)據(jù)的比較,結(jié)果發(fā)現(xiàn)一級上升段內(nèi)火箭的飛行速度、位置與設計預示值之間的偏差存在極性穩(wěn)定、幅值增加增大的特點，尤其是Y向速度偏差甚至超過5%，遠大于預期值;本文針對該現(xiàn)象開展機理分析，最終確認現(xiàn)在長征系列火箭普遍采用的“姿態(tài)角偏差+角速度”控制方案對程序角持續(xù)變化的工況存在幅值及極性較為穩(wěn)定的靜差，該角偏差持續(xù)作用下，將導致X向和Y向速度及位置偏差;針對該機理，探索、比較潛在的解決措施，最終確定采用實現(xiàn)簡便、控制效果好的“姿態(tài)角偏差+角速度偏差”雙偏差姿態(tài)控制方案;仿真結(jié)果表明，雙偏差姿態(tài)控制方案能顯著提高助殘骸落點精度及段軌道精度、降低氣動載荷，有利于火箭飛行品質(zhì)的提升。

運載火箭; 軌道精度; 姿態(tài)控制; 系統(tǒng)性規(guī)律

Absract: For explaining the reason of China’s long march series of rocket wreckage landing point is in front of the expected one,through comparing many times flight data , we find during the first ascending stage,the flight position and velocity are systemic different from the normal trajectory data，especially the error or Vy even exceeding 5%,which is not acceptable during the design period.And finally we assure the mechanism behind the phenomenon is the attitude control law of “attitude angle deviation+ attitude rate”,which is widely used by Long March rockets.After comparing several potential ways,the “double deviation attitude control scheme” of “attitude angle deviation+ attitude rate deviation” is selected,which can significantly improve the precision of trajectory accuracy and wreckage landing accuracy, reduce the aerodynamic load, improving the quality of the rocket flight.

0 引言

隨著科技水平的進步，空間發(fā)射任務朝著多樣化、復雜化和集成化的方向發(fā)展。各個新構(gòu)型火箭層出不窮，火箭的結(jié)構(gòu)也越來越復雜，目前航天事業(yè)對火箭性能的要求也越來越高。為了適應當前航天發(fā)展任務多樣化的要求，材料、結(jié)構(gòu)、控制、電氣等專業(yè)均提出了新的要求。控制系統(tǒng)能夠保證運載火箭的穩(wěn)定性和入軌精度，在其發(fā)射過程中的任務非常重要。近年來，諸多專家和學者對于運載火箭控制系統(tǒng)設計展開了廣泛、深入的研究，并且取得了諸多進展。

文獻[1]基于自適應控制理論設計了運載火箭的姿態(tài)控制系統(tǒng)，能夠通過控制器參數(shù)的自適應變化，從而保證系統(tǒng)的穩(wěn)定性、入軌精度及對干擾的魯棒性。文獻[2]采用自抗擾+分數(shù)階控制器的方案，通過擴張狀態(tài)觀測器將系統(tǒng)存在的內(nèi)外干擾進行測量，并通過分數(shù)階控制器進行補償，保證了系統(tǒng)的魯棒性，提高了系統(tǒng)的設計裕度。但是以上文獻采用方法在工程實現(xiàn)上比較困難，傳統(tǒng)的運載火箭控制方案采用“姿態(tài)角偏差+角速度”，有效保證了系統(tǒng)的穩(wěn)定性。但是采用這種控制方案會產(chǎn)生較為穩(wěn)定的偏差，在這種偏差的持續(xù)作用下，會產(chǎn)生速度及位置偏差，進而影響運載火箭的入軌精度。

基于以上研究，本文從工程實際應用角度出發(fā)，采用“姿態(tài)角偏差+角速度偏差”的雙偏差控制方案，設計了一種改進姿態(tài)控制方案，有效減少了傳統(tǒng)方案引起的靜差。保證了系統(tǒng)的準確性和工程易實現(xiàn)性。

在對比運載火箭飛行數(shù)據(jù)與設計數(shù)據(jù)中發(fā)現(xiàn)，二者的速度、位置、俯仰姿態(tài)角偏差及氣動載荷因子qα普遍具有極性及幅值穩(wěn)定的偏差，其中一級飛行段尤為明顯。圖1、圖2分別給出某火箭一級飛行段速度、位置及俯仰角速度、角偏差對比結(jié)果，一級分離時刻飛行軌道相對于標準彈道的偏差較大，其中X向飛行速度較設計值偏低約22 m/s，Y向飛行速度則較設計值則偏高約27 m/s。本文旨在探索該差異背后的技術(shù)機理，并提出控制改進方案。

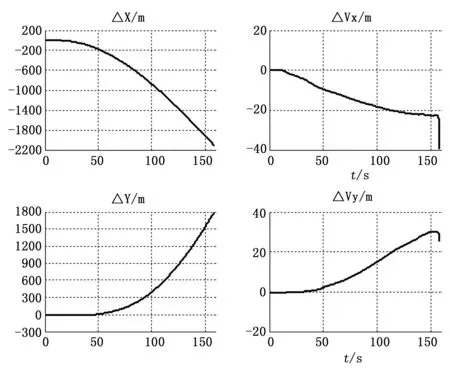
圖1 X、Y向位置偏差及速度偏差對比

1 差異性原因分析

1.1 標準彈道計算用姿態(tài)模型及控制方程

標準彈道設計時，按瞬時平衡假設，即認為控制提供足夠大的姿態(tài)調(diào)整能力，使得箭體姿態(tài)時時處于瞬時平衡狀態(tài)，角速度為0。對應的姿態(tài)方程及控制參數(shù)為如下公式[3]。

俯仰通道：

φ=α+θ

φa=φ+δφω

Δφ=φa-φP

偏航通道：

ψ=σ+β

ψa=ψ+δφψ

Δψ=ψa-ψP

1.2 姿態(tài)控制用姿態(tài)動力學模型及控制方程

為了便于與彈道計算結(jié)果對比，這里的姿態(tài)動力學方程也只考慮剛體項，而忽略推進劑晃動和彈性項[4]。此時的姿態(tài)動力學全量方程如下：

姿控采用的控制方程為：

1.3 彈道設計及姿態(tài)控制用動力學模型及控制方程差異性比對

對比表明：

(1)兩者使用的姿態(tài)動力學方程不同：彈道設計中姿態(tài)動力學按瞬時平衡考慮，而姿態(tài)控制中的動力學方程則考慮過渡過程；

(2)兩者使用的控制方程也是不同：彈道計算中僅考慮姿態(tài)角偏差項，而姿態(tài)控制則同時考慮角偏差及角速度項；

火箭飛行中，采用姿態(tài)設計用方案進行飛行姿態(tài)控制，即彈道設計采用的模型與飛行真實工況有差異。

下面分析以俯仰通道為例，分析實際飛行中模型差異導致的姿態(tài)及軌道偏差。為便于理解和表述，這里分析采用小偏差動力學方程。

火箭一級飛行段，通常在起飛后10s左右開始到一級關(guān)機前，利用引力進行持續(xù)小攻角低頭，具體表現(xiàn)為俯仰通道一直程序轉(zhuǎn)彎，即俯仰程序角速度不為零。理想狀態(tài)為火箭沿標準彈道無靜差飛行，此時有ωz=ωz_cx，故一級飛行段一直有一定幅值的俯仰角速度，故采用角偏差+角速度的控制方式時，俯仰通道必然存在極性穩(wěn)定的俯仰角偏差Δφ(Δφ≥0)。

該偏差的持續(xù)存在將對飛行彈道產(chǎn)生影響，具體為：

標準彈道設計中，攻角Δα為小量，，此時有Δθ=Δφ-Δα≈Δφ，而沿Y向的速度偏差量近似為VΔθ≈VΔφ>0，由于Δφ極性穩(wěn)定且有一定幅值，使得Y向速度及位置呈現(xiàn)系統(tǒng)性偏差。

我國的西昌、太原、酒泉衛(wèi)星發(fā)射中心均為內(nèi)陸發(fā)射場，子級殘骸落區(qū)為影響彈道設計乃至火箭設計的關(guān)鍵因素。在這3個基地發(fā)射的衛(wèi)星，一級飛行段均采用射程關(guān)機方案，以保證子級殘骸落點在允許的落區(qū)范圍內(nèi)，關(guān)機方程如下：

L=f1ΔVx+f2ΔVy+f3ΔVz+

f4ΔX+f5ΔY+f6ΔZ+fzΔt

其中各型號普遍為f2>f1，f5>f4。即長期存在、極性穩(wěn)定的俯仰姿態(tài)角偏差Δφ不僅影響軌道精度，同時影響關(guān)機時間：普遍使得關(guān)機時間較預期值有所提前，導致運載能力損失。

2 提高軌道精度的姿控改進措施

2.1 控制改進

上述分析表明，長征系列火箭一級飛行段普遍存在的Y向速度偏差現(xiàn)象的機理為彈道設計考慮的姿態(tài)控制模型與真實飛行工況不一致所致，因此要消除該系統(tǒng)性偏差，有如下3個潛在措施：

1)彈道設計采用飛行中的姿態(tài)角偏差+姿態(tài)角速度的控制方案，即計入程序角變化對姿態(tài)角速度及姿態(tài)角偏差的影響。該模式將導致需重新推導彈道設計適用的動力學方程，即該思路將導致彈道設計規(guī)范、設計流程、設計工具發(fā)生巨大變化，不利于工程實踐的可靠性。

3)改進控制方案。

若將姿態(tài)控制方案調(diào)整為姿態(tài)角偏差+角速度偏差控制(以下簡稱雙偏差控制)，即：

2.2 控制實現(xiàn)

飛行中的俯仰姿態(tài)角偏差Δφ通過箭體姿態(tài)角與程序角求差得到，即Δφ=φ-φcx。其中φ通過慣性平臺或捷連慣組獲取，而φcx則為時間變化的裝訂諸元。同理，Δωz≈ωz-ωz_cx，其中俯仰角速度ωz可以通過速率陀螺得慣性器件測量得到，俯仰姿態(tài)角速度ωz_cx也可以與俯仰程序角類似，通過諸元裝訂實現(xiàn)。但為了降低諸元裝訂的復雜性，同時也為了提供數(shù)據(jù)的匹配性，建議采用在線計算方式實現(xiàn)，具體為：

3 控制改進效果分析

3.1 對一級飛行段的影響分析

對比兩組工況的仿真時間表明，采用雙偏差控制后Y向速度和位置偏差量下降，相同關(guān)機量對應的計算機關(guān)機時間推遲約0.5 s，增大分離時的速度增量約25 m/s，對應運載能力在5 kg以上。

另外，采用雙偏差控制將使得Δφ下降，這也有利于氣動載荷qα的下降，零風標準彈道下qα相差220Pa左右，高空風補償彈道對應的qα下降幅度可達1 000Pa，對飛行安全性的貢獻顯著。

3.2 一子級殘骸落點精度的影響對比

按一子級耗盡關(guān)機考慮，仿真獲得一子級分離時刻的速度、位置，再計算一子級殘骸落點。標準彈道的射程Lx=590.466 km，雙偏差控制對應的射程為Lx=590.12 km，落點橫移L=8.06 km；角速度控制對應的射程Lx=599.58 km，落點橫移L=8.36 km。角速度偏差控制對應的射程與標準彈道一致，而角速度控制對應的射程較標準彈道前移9 km，該項主要是由于Y向速度偏大所致。

圖3、圖4給出不同控制策略的仿真結(jié)果，結(jié)果表明采用雙偏差控制方案能有效降低縱向落點偏差(原方案普遍具有落點靠前的特點)。

圖3 一子級殘骸縱向落點對比(橫軸s,縱軸km)

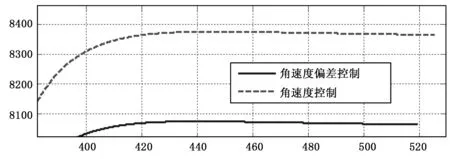
圖4 一子級殘骸橫向落點對比(橫軸s,縱軸m)

3.3 對二級飛行段的影響分析

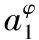
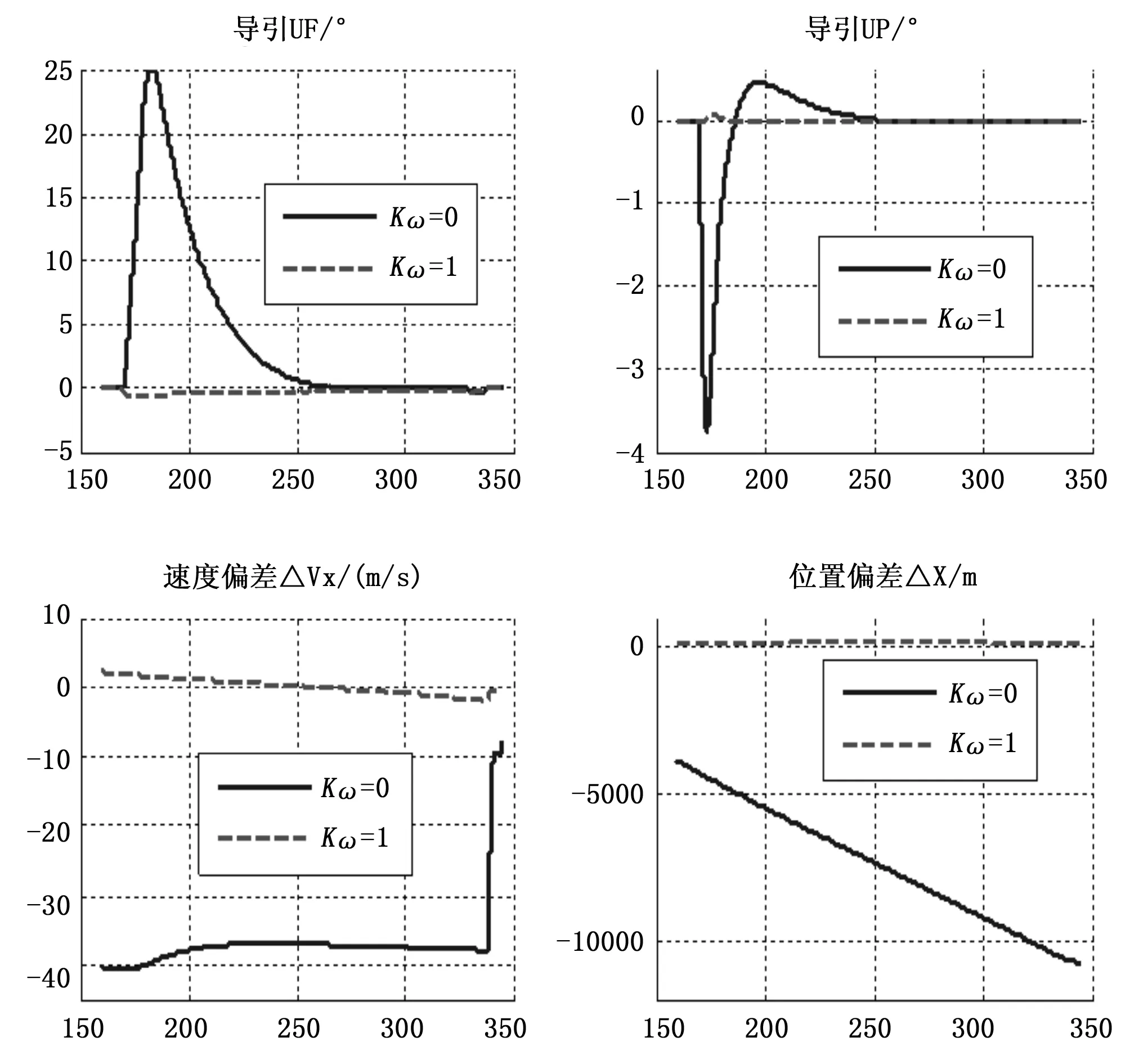
圖5 導引及X向速度、位置偏差

若改用雙偏差控制，則二級飛行段段導引不再出現(xiàn)長時間飽和現(xiàn)象，即軌道及姿態(tài)精度均提升，二級飛行段的關(guān)機時間將因此提前0.5s以上，型號飛行中曾經(jīng)出現(xiàn)過的二級耗盡關(guān)機事件也將不再發(fā)生，提高可飛行的精度和可靠性。

圖6 Y、Z向速度及位置偏差比較

4 結(jié)論

全量仿真發(fā)現(xiàn)不同控制策略下飛行軌跡與標準彈道較為明顯的差異，理論分析結(jié)果表明，是由于標準彈道所采用的控制模型與現(xiàn)有方案不同所致，據(jù)此提出“姿態(tài)角偏差控制+姿態(tài)角速度偏差”的雙偏差控制方案，該方案有利于提高一、二級的軌道飛行精度，降低殘骸落點偏差，有利于提升火箭的飛行安全性飛行品質(zhì)。

[1]OhCS,BangH,ParkCS.Attitudecontrolofaflexiblelaunchvehicleusinganadaptivenotchfilter:groundexperiment[J].ControlEngineeringPractice, 2008, 16(1): 30-42.

[2] 程昊宇, 董朝陽, 王 青. 運載火箭的抗干擾分數(shù)階控制器設計[J]. 系統(tǒng)工程與電子技術(shù), 2015, 37(9): 2109-2114.

[3] 龍樂豪, 液體導彈與運載火箭系列總體設計[M]. 北京:宇航出版社, 2001:267-270.

[4] 楊云飛，陳 宇，李家文，等. 運載火箭搖擺發(fā)動機與全箭動力學特性耦合關(guān)系研究[J]. 宇航學報，2011(10).

[5] 李 輝，王 波，郝興偉. 運載火箭導航計算子系統(tǒng)建模與仿真[J]. 系統(tǒng)仿真學報，2006(2).

[4] 李 輝，敬曉剛，徐利梅. 基于Matlab/Simulink的運載火箭6自由度運動仿真[J]. 宇航學報，2005(5).

A New Attitude Control Approach to Improve Trajectory Accuracy

Li Jun1,2, Cheng Xing2, Chen Yu2，Zhang Puzhuo2, Dong Chaoyang1

(1.Beijing University of Aeronautics and Astronautics,Beijing 100191，China; 2.Beijing Institute of Aerospace Systems Engineering, Beijing 100072,China)

launch vehicle; trajectory accuracy; improved attitude control approach

2016-09-08；

2016-12-23。

李 君(1977-)，男，重慶彭水人，博士，高級工程師，主要從事運載姿態(tài)動力學建模與控制、總體設計與優(yōu)化方向的研究。

1671-4598(2017)05-0087-04DOI：10.16526/j.cnki.11-4762/tp

TP

A