遺傳算法求解旅行商問題

程榮

摘 要：旅行商問題是一個組合優化問題，具有重要的實際意義。而遺傳算法是求解旅行商問題的典型算法之一。本文首先介紹了旅行商問題的定義以及它的研究背景、發展現狀和常用算法。在此基礎上，詳細闡述了遺傳算法原理。通過改進這些算子，改進了傳統的遺傳算法，提高了算法的效率，降低了它的時間及空間復雜度。本文使用路徑總長度的倒數作為適應度函數，保證了解向著最優化方向發展。然后選擇部分交叉算子來產生新個體，保證了迭代的效率。變異算子利用位點變異，使算法變得簡單，易行。最后，使用MATLAB 語言進行編程，解決了城市數目分別為15和25時的兩個實際問題。通過對這兩個問題的收斂速度的對比、分析，總結了遺傳算法求解旅行商問題的特點。

關鍵詞：旅行商問題； 遺傳算法； MATLAB

旅行商問題是優化組合問題研究中一個著名而經典的問題，它的研究價值也就不言而喻。在實際問題里，一個大家都熟知的例子就是利用機器給電路板鉆孔的優化設計問題。此外旅行商問題的實際應用還體現在交通管理規劃方面。交通管理的主要的目的是在復雜的地理網絡結構中優化決定車輛的線路來減少交通費用。旅行商問題的應用例子還包括：設計安全，合理，有效率的交通網，從而減少交通擁堵；如何來規劃出更好地物流線路，縮小運營界產生的成本，減少資源消耗等。

由于旅行商問題具有這么重要的實際意義，求解旅行商問題算法也就隨之發展起來。最早的解決方法是線性規劃，后來陸續產生了多種求解旅行商問題的算法。其中大致可以分為精確算法，近似算法，智能算法。精確算法：線性規劃，動態規劃，分支定界；近似算法包括：插入法，Clark& Wright算法，生成樹算法，最近鄰算法，概率算法等。近年來也出現了許多新的智能算法。像諸如模擬退火，蟻群算法以及遺傳算法等等。

本文首先介紹了什么是旅行商問題，然后簡單介紹了目前解決旅行商問題所用到的一些算法。之后詳細介紹了什么是遺傳算法，遺傳算法的實現原理，以及遺傳算法的構成。然后利用常用的MATLAB軟件，使用遺傳算法解決了幾個實際問題。通過算法以及結果分析，找出遺傳算法的優缺點，并進一步提出了改進的遺傳算法。

1 旅行商問題

1.1 問題描述

旅行商問題，也叫貨郎擔問題，目的是求解最優線路，是一類經典的規劃類問題。旅行商問題是指，一個旅行商，要去往n個不同的城市，需要每個城市都去，并且僅僅去一次，再回到最初的城市，形成一個環路，從眾多可能路徑中求解出一個最短的路徑。

1.2 數學模型

我們將xij設定為決策變量。沒有直接從城市i到達城市j的路線，我們將其賦值為xij=0。如果商人直接從城市i到達城市j，我們用xij=1來表示。我們在上述模型得到的5個式子中，第一個式子保障了路徑之和最小，第二個和第三個式子分別保障從某個城市出來和進入都只是一次。而第四個式子則保障了走過的所有路徑都沒有回路。其中C表示集合C中元素個數。

2 算例分析

2.1 問題描述

一個旅行商人要從某一個城市出發，經過所有的城市，并且每個城市只能走一次。最終回到出發的城市，求解一個最短路徑。

2.2 問題分析

1）編碼方式。

我們這里使用十進制編碼方式。把旅行商途經的城市的順序序號作為遺傳算法的編碼。假設15 個城市的序號為1，2，…，15，那么它的任意一個全排列i1，i2，…，i15就是一個數據編碼，表示一個染色體，每個染色體就代表一個解，不同解是靠染色體上不同的基因i決定的。

2）適應度函數。

由于旅行商問題的規劃模型的目標函數是要求解最小值，所以適應度函數就用路徑的總長度的倒數來表示。這樣，符合了遺傳算法的優勝略汰的搜索策略。

3）初始群體的產生。

隨機生產一個大小為N且每條染色體上的基因長度都是的n初始種群，作為第一代個體。

4）選擇過程。

我們需要構造一個∑f（xi）合適的隸屬函數p=f（xi）∑f（xi）。然后計算出種群中每個遺傳個體的適應度f（xi），從而得到種群中遺傳個體適應度的和。那么我們就可以用來表示個體被選中的概率。

5）交叉過程。

首先設定交叉概率pc=0.9。其次，根據這一概率，選出要進行交叉操作的個體，并將它們兩兩配對。然后在染色體上1～n-1個基因編號之間隨機地選出兩個，之間的基因作為接下來將要進行交叉的對象。

6）變異過程。

進行完交叉操作后，以變異概率pm=0.2從群體中選出要進行變異的遺傳個體。然后，隨機地從1～n-1之間選擇兩個數作為變異點，將基因進行交換。

7）復制操作。

復制過程就是將適應度值打的個體直接復制到下一代，從而不至于丟掉性質較優的解。

2.3 問題求解結果

將程序放到MATLAB軟件中執行，得到了如下結果：

2.3.1 城市數為15時的運行結果

（1）隨機產生的初始解的路徑總長度為4.7950e+004。

（2）迭代次數設置為c=100時的最優解路徑的總長度為：2.5025e+004。

可以看出，迭代100次，產生了不錯的優化效果。

但這是不是接近最終的最優解呢？下面我們又將迭代次數設置為了C=200，路徑總長度為：2.4619e+004。

通過兩結果進行比較知，迭代100次時基本上得到了近似最優解，而且迭代次數越多，得到的解越優。

2.3.2 城市數為25時的運行結果

（1）隨機產生的初始解路徑總長度1.1297e+005。

（2）迭代次數設置為c=100時的最優解路徑總長度為46737e+004。

（3）迭代次數設置為C=300時路徑總長度為：4.5038e+004。

容易看出，當城市的個數增加到25個時，迭代100次產生的結果與最優解的偏差還有點大，需要繼續迭代。

繼續進行迭代次數為500時的實驗，路徑總長度為： 44838e+004。這一結果接近200次迭代的解。也就是當迭代次數到200次時，為近似最優解。

2.4 結果評價

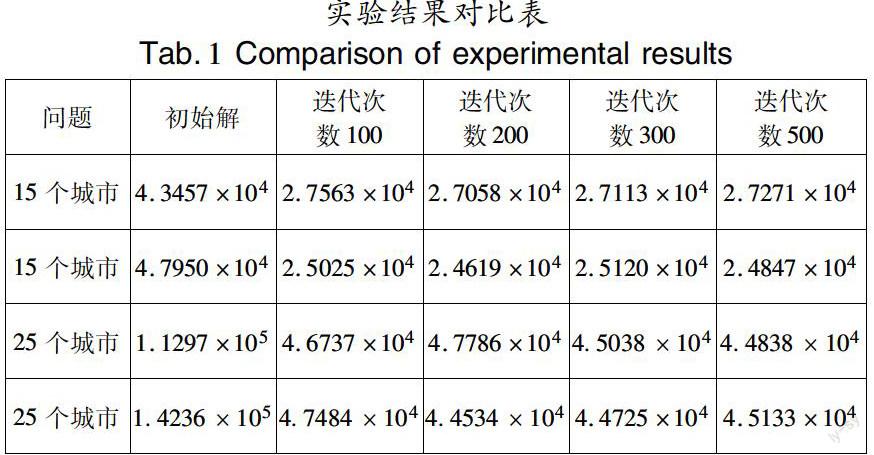
通過運用遺傳算法對上面兩個問題（城市數分別為15和25）求解結果可以看出，運用遺傳算法能夠求解旅行商問題。對于同一個問題，隨著搜索次數的增多，所得到的解一般會在一定范圍內波動，并且越來越好。但當增加到某一值時，函數的收斂會趨于平緩（這時可以認為達到了最優解）。通過15個樣本城市和25個樣本城市的迭代求解過程可以發現，當我們的樣本數量比較多時，我們需要的循環搜索的次數就越多，求解完成需要的時間就越長。而且，通過上面的結果對比表我們可以發現，遺傳算法求解過程中，初始解是隨機產生的，對于每一次的求解，初始解的不同，問題收斂的情況也就不同，產生的最終解也不同。由此可見，遺傳算法對初始解比較敏感，而且由于初始解是算法隨機生成，不能人為控制，所以不容易把握。

參考文獻：

[1]于瑩瑩，陳燕，李桃迎.改進的遺傳算法求解旅行商問題[J].控制與決策，2014（8）：1483-1488.

[2]威廉·J·庫克，J.Cook，郭凱聲.旅行商問題[J].環球科學，2012（7）：19.

[3]章新華.遺傳算法及其應用[J].火力與指揮控制，1997，18（4）：59-64.

[4]吉根林.遺傳算法研究綜述[J].計算機應用與軟件，2004，21（2）：69-73.

[5]梁艷春，馮大鵬，周春光.遺傳算法求解旅行商問題時的基因片段保序[J].系統工程理論與實踐，2000，20（4）：7-12.

[6]周明，孫樹棟.遺傳算法原理及應用[M].國防工業出版社，1999.

[7]李敏強，徐博藝.遺傳算法與神經網絡的結合[J].系統工程理論與實踐，1999，19（2）：65-69.