虹橋機場航班智能調度問題

摘 要:機場航班智能調度已經逐漸納入評價機場的重要條件之一,目前機場調度規則大多還是人工決策模式。本文針對曾發生嚴重 A 類穿越事件的上海虹橋機場航班調度建立了跑道服務智能調度模型,提高了飛機調度安全和提高準點率和起降效率,與人工管理相比,極大地提高了機場的安全性能和利用率。本文建立了基于遺傳算法和元胞自動機模型的目標規劃模型,首先建立基本的安全等待模型,將機場抽象為有向節點圖,滑行道抽象為隊列結構,規定滑行道上只有節點處能停放飛機,借用元胞自動機的方法,模擬了飛機在滑行道上的運動情況。為了能較真實地模擬實際飛機的運動情況,得到更有價值的模擬數據,我們設定了一組描述飛機單向滑行和排隊等待的的狀態變換規則。我們重點考慮了飛機運動的起始條件,終止條件,前進條件,排隊等待條件,變道條件和穿越跑道條件等,以期保障飛機起降時絕對的安全性。其次,我們建立了運行效率較高的安全等待模型,設定了準點率和起降效率的具體形式,我們用計劃與起飛時間的殘差和和準點的飛機與總的飛機的比值共同描述飛機的準點率,用飛機在滑行道上的等待時間描述起降效率。
關鍵詞: 機場調度;元胞自動機模型
一、問題重述
(一)問題背景
2016 年 10 月 11 日,上海虹橋機場發生了由于人工調度而引起的安全事故。塔臺空管人員的人工指揮的失誤,造成東航一家 A320 客機在滑出跑道即將起飛時,發現另外一家 A330 客機正在橫穿跑道,不得不從 A330 的上空強行掠過,倘若沒有 A320 機長的決斷,這將會是一場可怕的空難。因此,人工決策不能有效的解決機場調度的安全問題和運行效率問題,智能調度模型的建立和運用將會是解決機場安全問題和提高機場運行效率的一種穩定性好的,可行性高的,可操作性強的解決方案。
(二)問題提出
借助計算機建立一種智能調度模型,在保證絕對安全的前提下提高機場的運行效率,調度內容主要包括航班的實時起飛降落時間,以及航班起飛前和降落后的地面規劃路徑。
問題 :依據附件 1 所示的上海虹橋機場地形圖和附件 2 所列的 2017 年某日下午一小時內的預降落和起飛航班信息,設計一個跑道服務智能調度模型,調度內容包括空中飛機降落時間及降落后的運動規劃,以及地面飛機起飛前的運動規劃及起飛時間,安排所有航班的起飛和降落(包括次序、時間、地面滑行路徑)。調度模型優先考慮跑道上飛機的安全,防止 A類穿越事件發生,在此基礎上考慮提高準點率和起降效率.(當時機場的風向為由北向南,風速為 20km/h,飛機逆風起飛,逆風降落,滑行速度假設為 10節/小時.)
二、模型假設
(一)基本假設
附件 2所給的航班信息數據真實可靠;
每架飛機在同一跑道上起飛所需的時間相同;
不考慮天氣、空中交通管制等其他因素對飛機等待時間的影響。
(二)針對有向節點圖的假設
機場跑道僅用作飛機的起降,而不充當滑行道;
飛機等待起飛的滑行道為 6 和 7;
飛機只在橫向滑行道上穿越跑道;
只考慮起飛飛機在滑行道上等待起飛的時間,不考慮它從停機坪到滑行道入口的運動時間;
降落到T2 航站樓的飛機穿越起飛跑道后即完成降落,不考慮之后的運動;
平行滑行道 B 只允許飛機單向通行。
三、模型建立
(一)問題分析
在問題一中我們需要解決的是如何刻畫安全的狀態,我們選取兩種特殊的情況分析,其一,跑道上有飛機時,此時處于滑行道的飛機應該設為等待狀態,其二,滑行道前方有飛機時設為等待狀態。同時設定 0-1 狀態變換規則集,規定后方飛機不能超越前方飛機,相向飛機不允許相遇,飛機之間保留有最小安全間隔。因此,在這些約束下,我們將定量問題轉換為邏輯判斷進行安全性能的刻畫。同時,設定指標集,設定準點率為計劃時間和起飛時間的殘差和,設定起降效率為所有飛機的等待的時間和。利用這兩個指標可以定量的描述智能調度模型的性能。
(二)模型的準備
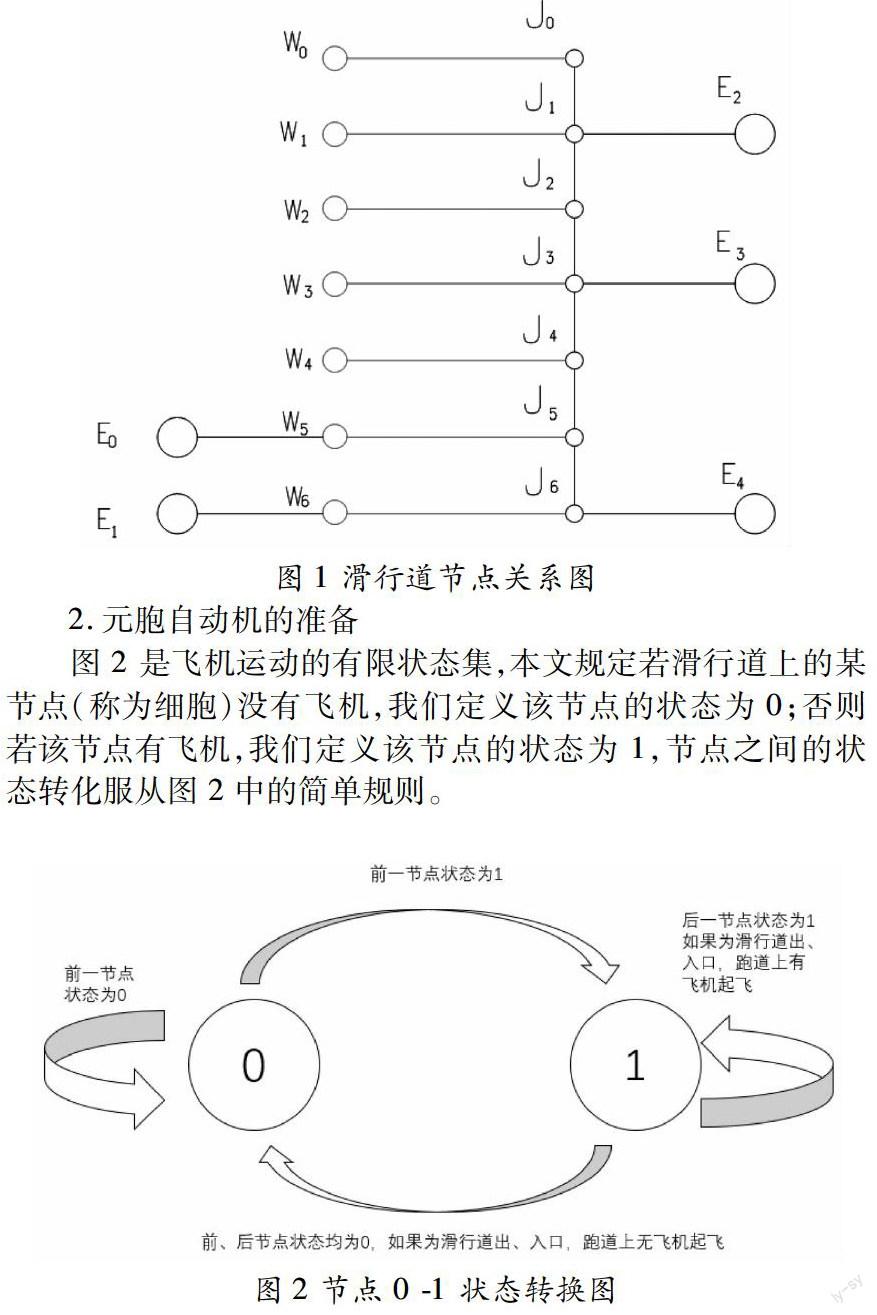
1.地圖的準備
(三)基本安全模型的建立
這是研究飛機在滑行道上等待的基本模型,建立在安全的前提下。因為已有假設,飛機在滑行道上的的運動都是速度為 10 節(308/m/min)的勻速運動,由此計算得滑行道上的安全間隔距離約為 30m;根據文獻資料,滑行道的寬度只能允許一架飛機通過,所以假設飛機在所有滑行道上單向運動。在本題情況下,我們假定降落的飛機在中間平行滑行道上只能向北單方向運動,在橫向滑行道中職能向西單方向運動,這樣就可以防止飛機相遇、相撞等事件發生。
下面是本文設定的滿足安全條件的約束規則,主要是從飛機起飛、降落和轉移三種情況出發, 根據附件 2 中飛機基本從 T2 航站樓出發或停靠到 T2 航站樓,可將 T2 航站樓的飛機作為主要研究對象,而將少量的 T1 航站樓的飛機等效于一個全局的時間延遲。同時,根據飛機路線分配的就近原則和起飛與降落的相互制約關系,可以手動指定以下初始的路線分配。
(五)模型的求解
將機場滑行道布局為有向圖, 將跑道圖轉化為節點圖,并且針對節點圖中節點的關系,建立隊列圖 2。
元胞自動機的模型假設。
1)不同飛機,型號不同,占有的節點數不同,單位周期移過的節點數也不同,具體大小根據滑行道長度和飛機長度確定;
2)飛機在改變方向和穿越跑道時不需要額外的時間;
3)每個細胞單元的長度約為 30m,寬度為滑行道的平均寬度 60m。不同滑行道由于長度的不同,上面的細胞個數也不同;
4)模擬的時間單位為 1分鐘,即每次刷新飛機的狀態,都經過 1分鐘。
根據元胞自動機的原理,我們很容易在建立碰撞不相撞的規則,設跑道上的節點為主節點,滑行道上的節點分為頭節點和尾節點,建立隊列的關系圖,如圖3所示。
1)如果主節點被占用,則尾節點的飛機處于等待狀態,該架飛機的 0-1 狀態不改變,相當于等紅綠燈的狀態。
2)如果主節點未被占用,則尾節點中的飛機可以行進,該節點的 0-1 狀態改變。
3)兩個隊列的頭節點和尾節點是常量,不會改變。
4)如果某個細胞的尾節點的一個細胞的狀態為 1,則該細胞內的飛機處于等待狀態。
5)如果某個細胞的尾節點的一個細胞的狀態為 0,則該細胞內的飛機可以行進。
參考文獻:
[1]楊秋輝,游志勝,馮子亮,樊鴻.自適應遺傳算法在飛機調度問題中的應用.四川大學學報,2004.
作者簡介:王昱(1996-),漢族,女,陜西人,本科,就讀西北工業大學理學院數學與應用數學專業。

